輔助微分方程完全匹配層在聲波方程數值模擬中的應用

趙建國，史瑞其，陳競一，趙維俊，王宏斌，潘建國

1.中國石油大學（北京）地球物理與信息工程學院/油氣資源與探測國家重點實驗室/CNPC物探重點實驗室，北京 102249

2.中國海洋石油研究總院，北京 100027

3.塔爾薩大學地球科學學院，美國 塔爾薩 74104

4.沈陽地質礦產研究所，沈陽 110034

5.中石油勘探開發研究院西北分院，蘭州 730000

0 引言

在地震波數值模擬中，為了在有限計算區域模擬無限大區域中地震波的傳播，需要對計算區域截斷邊界給出吸收邊界條件以消除邊界處產生的虛假數值反射。目前，廣泛使用的主要有2種構造吸收邊界條件的方式：一種是通過波動方程因式分解獲得單行波方程的旁軸近似邊界條件，如Clayton－Engquist吸收邊界條件［1］、廖氏吸收邊界條件［2］、Higdon吸收邊界條件［3］等；另一種是在邊界上引入吸收介質，使得地震波在無反射地進入吸收介質后被衰減掉，如完全匹配層（pefectly matched layer，PML）［4］。PML作為一種高效的吸收邊界，在地震波正演中被廣泛使用。PML最初采用對波場變量進行非物理場分裂的方式來實現，使得計算內域與PML吸收邊界區域的數值計算格式完全不同，實現方式較為繁瑣。后來，復拉伸坐標［5］概念的引入使得PML可以通過非分裂場方式實現。

在使用非分裂場方式實現PML的算法中，需要引入輔助變量并在時間域迭代中對其進行更新。通過輔助變量更新方式的不同，可以劃分出一系列不同的PML算法，如通過遞歸積分［6］和遞歸卷積［7］算法。以上算法使得輔助變量的時間計算格式局限于時間二階精度。但是，在波動方程數值模擬中，為了獲得更高的模擬精度，常常需要使用高階時間遞推格式；因此，上述非分裂PML在這種情況下的應用受到限制。針對該問題，作者介紹了一種通過輔助微分方程求解輔助變量的 ADE－PML（auxiliary differential equation PML）［8］算法，將其用于高階時間精度（四階Runge－Kutta）的聲波方程數值模擬中。通過數值模擬，考察ADE－PML在高階精度時間遞推格式聲波方程模擬中的應用效果并進行理論分析。

1 方法原理

在二維直角坐標系下，聲波方程的一階壓力－速度形式在時間域如下：

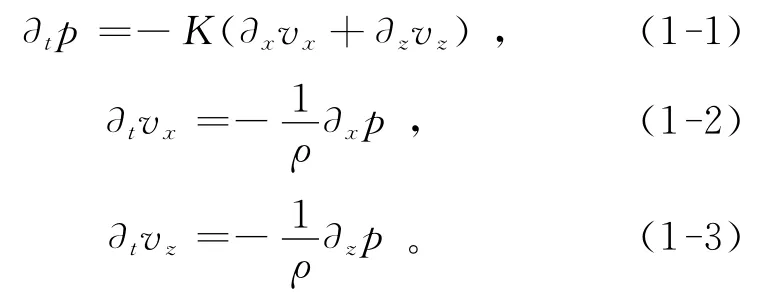
其中：p為聲壓；體積模量K＝ρc2，ρ為質量密度，c為聲波在介質中的傳播速度；vx和vz分別為沿x和z方向的速度場分量。注意，這里vx和vz是指介質中質點振動速度，c為波在介質中傳播的群速度。

本節將介紹一種使用輔助微分方程在時間域更新輔助變量的非分裂完全匹配層算法，這種方法可以適應高階精度的時間遞推格式。本文以四階Runge－Kutta時間遞推格式為例說明ADE－PML在高階時間遞推格式中的應用。為構造PML，需要對空間偏導數做復拉伸坐標變換。為簡單起見，首先以x方向為例，只討論x正半坐標軸的形式，并假設PML區域從x＝0開始。然后將x坐標替換為復拉伸坐標：

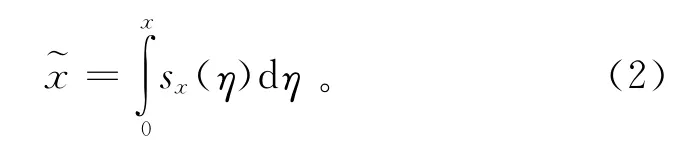
其中：sx是復拉伸函數，決定著PML的吸收效果。則關于x方向的偏導可以改寫為

z方向同理。因此，只需將關于x，z方向的偏導?x，?z替換為復拉伸坐標下的??x和??z后即可。由于PML需在頻率域導出，以式（1－1）的頻率域方程為例：

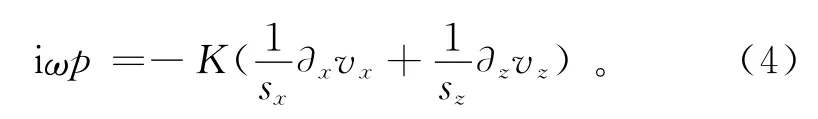
其中：i為虛數單位；ω為角頻率。當確定復拉伸函數sx，sz的具體形式后，即可將式（4）變換回時間域。傳統的復拉伸函數為

其中：dx≥0是使地震波振幅在PML內呈指數級下降的衰減系數。由于式（5）只對行波有效，對平行于PML和計算內域交界傳播的隱失波和極低頻波無效［9－10］，因此，只能增加 PML厚度或將震源放置于遠離PML的位置，用以增加內存和計算時間。為解決這個問題，Kuzuoglu等［11］將復拉伸函數的概念擴展，提出了復頻移拉伸函數：

其中：κx和αx為輔助衰減系數；κx≥1，作用是將傾斜入射波矯正為垂直入射波；αx≥0使復平面的極點從實軸移動到虛負半平面上，作用是消除切入射波引起的低頻波和隱失波。為避免數值反射，各衰減系數需要漸進變化。當取κx＝1和αx＝0時，式（6）即退化為傳統復拉伸函數（5）。筆者主要采用指數函數［12－14］來定義 PML 的衰減系數分布：

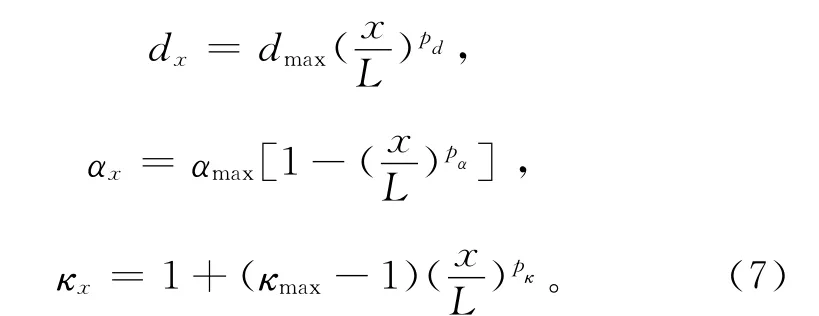
其中：L是PML厚度；pd，pα和pκ為常數，通常取pd＝2，pα＝1，pκ＝2；dmax，αmax和κmax的最優值依賴于計算模型參數或所選數值模擬方法。根據文獻［12］，衰減系數dmax通過關于垂直入射平面波的目標反射系數R計算：

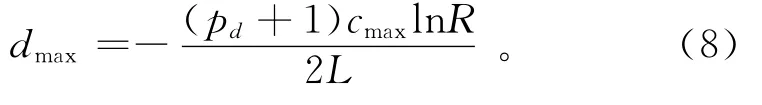
其中：cmax為計算模型的最大聲波速度。根據文獻［13］和［14］，輔助衰減系數αmax和κmax由以下關系確定：

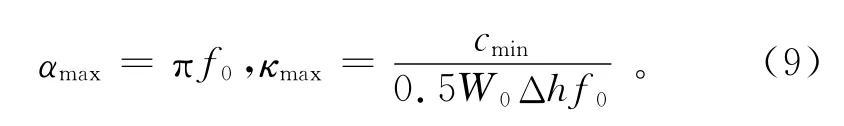
其中：cmin為計算模型的最小聲波速度；W0為當前所用空間離散格式每個波長所需的最小采樣點數；Δh為最大網格間距；f0為震源中心頻率。

ADE－PML的主要思想為將1/sx分解為2項之和，并使得iω只存在于其中一項的分母中：

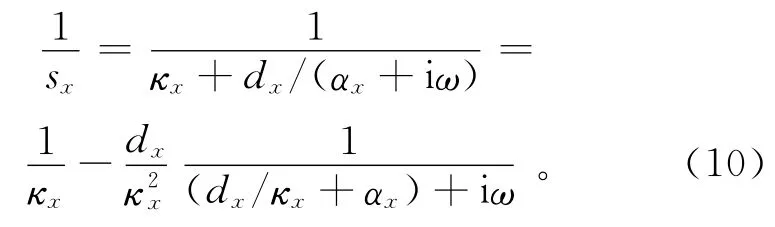
則式（4）轉化為

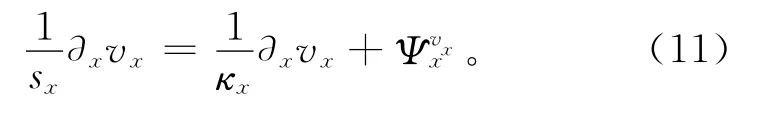
其中，為與空間偏導數?xvx相關的輔助變量，定義為

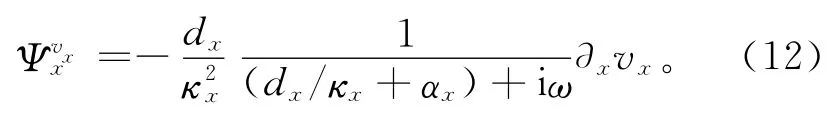
將式（12）改寫為

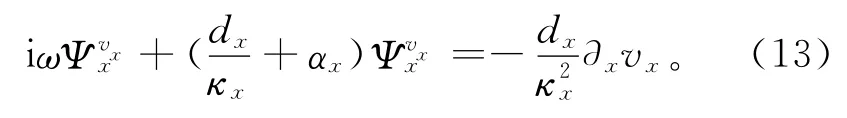
將式（11）代入式（5），由頻率域變換回時間域后，得到非分裂形式的PML方程（同理處理項）：

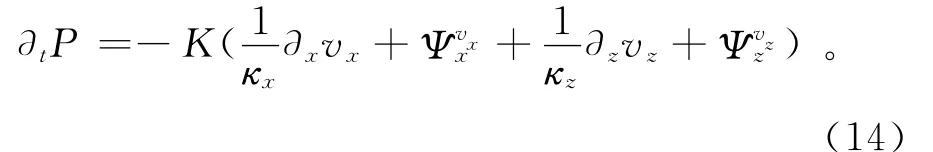
可見要得到時域PML方程，只需將空間偏導項?xA替換為?xA/κx＋ψx即可。將式（13）變換回時間域，得到關于輔助變量的微分方程：

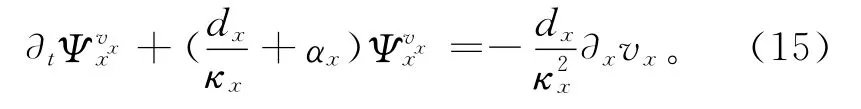
同理可得關于的輔助微分方程。ADE－PML的特點在于通過直接在時間域離散微分方程式（15）來求解輔助變量，因此適用于任意時間精度的遞推格式的數值模擬。下面以四階Runge－Kutta（以下簡稱RK4）格式為例說明ADE－PML在高階時間精度聲波方程數值模擬中的應用。

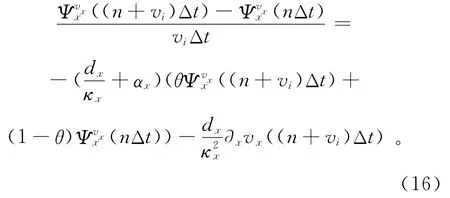
在時間域直接對式（15）進行RK4時間離散，輔助變量滿足其中：Δt為離散時間步長；下標i對應每個RK4循環中第i步迭代；當θ取0，1/2和1時，分別對應求取輔助變量的顯式、半隱式和隱式格式。對式（16）化簡可得

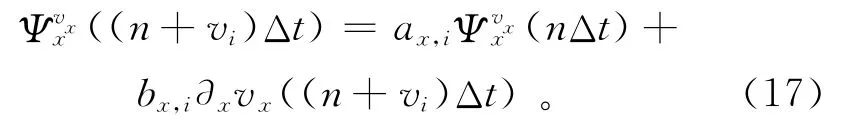
其中：

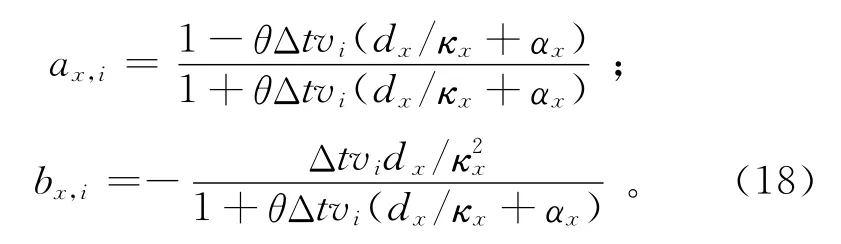
下面給出求解一階速度－壓力聲波方程式（1）的RK4時間遞推算法。設w＝（vx，vz，p），則由n時刻的wn更新n＋1時刻的wn＋1的過程可表達為

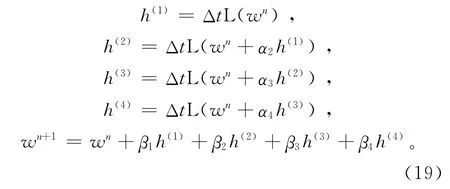
其中：算子L（·）表示式（1）中等式的右端項；RK4系數α2＝1/2，α3＝1/2，α4＝1；β1＝1/6，β2＝2/6，β3＝2/6，β4＝1/6。

2 數值模擬

為驗證ADE－PML的吸收效果，使用四階精度旋轉交錯網格［15－16］進行空間離散。模型計算區域為一5 200m×1 600m的長方形區域，由651×201個網格點構成，有限差分元胞邊長為Δx＝Δz＝8 m。介質密度ρ＝2 000kg/m3，聲波速度cp＝3 000 m/s。時間上采用RK4高階時間更新格式，這里取Δt＝1.2ms，模擬持續時長3.6s，共計3 000時間步。采用點聲壓震源激發，震源子波為一導數高斯函數，其中a＝（πf0）2，震源中心頻率f0＝15Hz，子波時延t0＝1.2/f0＝0.06s，激發點位于（176m，496m）處；設置2個檢波點，檢波點1和檢波點2分別位于（1 456m，496 m）和（176m，4 896m）處；計算區域四周由PML吸收邊界包圍，厚度為80m，占10個有限差分元胞。震源和檢波點2靠近左側PML，檢波點1靠近右側PML。

為檢驗復頻移拉伸算子的效果，分別給出使用傳統拉伸算子（5）的ADE－PML（這里稱為非復頻移ADE－PML）和復頻移拉伸算子（6）的 ADE－PML條件下的模擬計算結果。

該算例中，由于震源靠近左側吸收邊界，形成了高角度入射PML的情況。從波場快照圖1a可見，非復頻移ADE－PML對高角度入射波衰減不完全，入射波在左側PML內形成損耗波，這些波產生了低頻虛假反射，且虛假反射能量隨著入射角度和傳播距離的增大而增強：從1.68s的波場可見，在遠偏移距低頻虛假反射明顯影響了求解區域的波場。而圖1b中復頻移ADE－PML邊界由于使用復頻移拉伸算子，對高角度入射波吸收很好，在左側PML內沒有產生損耗波和低頻反射，在圖1b中1.68s波場中，即使在遠偏移距也沒有可見的虛假反射。

在地震記錄圖2a中，隨著偏移距的增大，高角度入射產生的虛假反射振幅逐漸變強，在直達波同相軸之后出現了一些“拖尾”現象，這是由于波場快照圖1中在左側吸收邊界附近產生的低頻虛假反射所致，從圖1中1.68s的波場可見，在遠偏移距這些低頻反射尤為強烈。而圖2中復頻移ADE－PML由于使用了復頻移拉伸算子，對高角度入射波吸收很好，沒有出現圖1中的低頻虛假反射；在圖2中1.68s波場中，即使在遠偏移距也沒有產生可見的虛假反射，在地震記錄圖3b中，同非復頻移ADEPML相比（圖3a），復頻移ADE－PML條件下僅可見直達波同相軸而沒有產生圖3a中的“拖尾”現象。

從檢波點1地震記錄（圖3a）可見，在檢波點1處，非復頻移ADE－PML和復頻移ADE－PML的計算結果都與精確解（即解析解）吻合良好，說明在垂直或小角度入射情況下，使用非復頻移和復頻移拉伸算子都可以高效吸收外行波場能量。因此，復頻移拉伸算子對垂直入射波的吸收無明顯改善。

而從檢波點2的地震記錄（圖3b）中可見：非復頻移ADE－PML條件下的地震記錄上產生了明顯的虛假反射抖動，與參考解吻合不佳，這是因為檢波器2記錄到了高角度入射波產生的低頻虛假反射，這些虛假能量隨著偏移距增大而增強；而在檢波器2處，復頻移ADE－PML情況下的記錄與參考解吻合良好。這說明，復頻移拉伸算子對切入射波的吸收有明顯改善。

圖1 非復頻移（a）和復頻移（b）ADE－PML邊界條件下的聲壓場p的波場快照Fig.1 Snapshots of the pressure field pof acoustic wave in the non－CFS（a）and CFS（b）ADE－PML condition

圖2 非復頻移（a）和復頻移（b）ADE－PML條件下在直線x＝xs上接收到的地震記錄Fig.2 Seismograms recorded at line x＝xsin the non－CFS（a）and CFS（b）ADE－PML condition

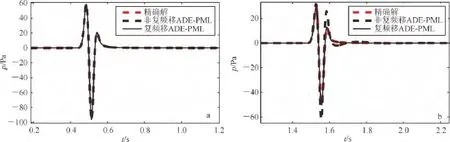
圖3 非復頻移和復頻移ADE－PML邊界條件下得到的檢波點1（a）和檢波點2（b）的聲波方程地震記錄同精確解的對比Fig.3 Seismograms calculated in non－CFS ADE－PML and CFS ADE－PML conditions at receiver 1（a）and receiver 2（b）

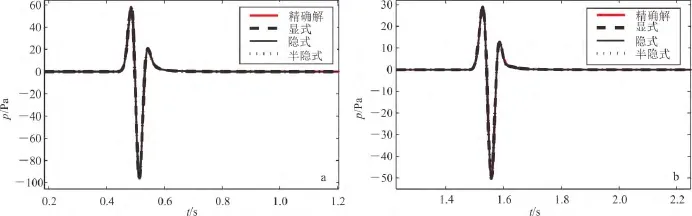
圖4 顯式、隱式和半隱式更新ADE－PML輔助變量條件下在檢波器1（a）和檢波器2（b）處得到的地震記錄Fig.4 Seismograms calculated using the explicit，implicit and semi－implicit update scheme for the ADE－PML auxiliary variables at receiver 1（a）and receiver 2（b）

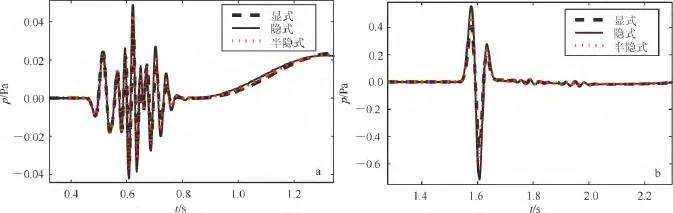
圖5 顯式、隱式和半隱式更新ADE－PML輔助變量條件下在檢波器1（a）和檢波器2（b）處得到的測試解同精確解的差異Fig.5 Differences between the test and reference solution calculated using the explicit，implicit and semi－implicit update scheme for the ADE－PML auxiliary variables at receiver 1（a）and receiver 2（b）

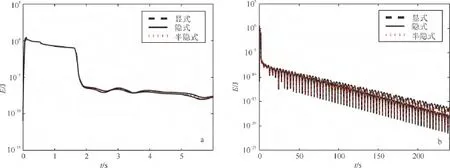
圖6 波場總能量衰減Fig.6 Total energy decay of the wavefield

如前文式（15）中所示，對于ADE－PML輔助變量的計算可使用顯式、隱式、和半隱式更新格式，這里分別對3種輔助變量的更新格式下的ADE－PML吸收效果進行了檢驗。如前述復頻移拉伸算子可以改善吸收效果，因此在復頻移ADE－PML邊界條件下計算。從圖4中可見，3種更新格式得到的地震記錄均無虛假反射振動，因為復頻移拉伸算子的作用，在檢波點2處也與精確解吻合良好。圖5中繪出了3種更新格式同精確解的差異曲線，用于細微比較三者的差異。從圖中差異曲線的擺動幅度可見，由于數值頻散效應在遠偏移矩的積累，圖5b的差異曲線比圖5a中的擺動大，無論是垂直入射的檢波點1還是高角度入射的檢波點2處，顯式格式比隱式和半隱式格式同精確解的吻合程度好。

圖6為3種更新格式在長時間數值模擬中（這里進行了2×105時間步，共240s的模擬計算）的波場總能量變化情況，從波場能量的變化情況可檢驗 ADE－PML吸收邊界的穩定性［7，13］。求解區域Ω中（不包括吸收邊界區域）的總能量E通過下式計算：

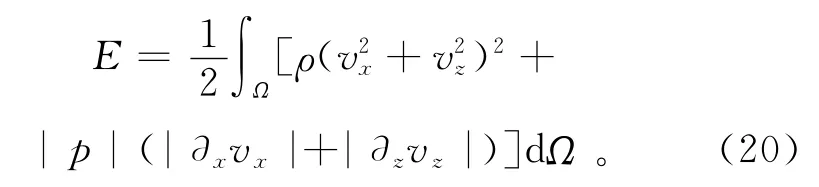
從圖6a可見：當數值模擬開始時（約0.1s左右），震源將能量注入介質使得總能量急劇上升；之后由于吸收邊界作用，波場能量開始逐漸下降。在約1.7 s時能量出現一個陡降，因為這時聲波完全離開求解區域，理論上講該時刻之后求解區域中的能量為虛假能量。由圖6b可見，在數值模擬后期（6s之后），波場總能量持續下降至10－20J數量級，說明顯式、隱式和半隱式記憶變量更新格式都具有長時間穩定性，并且仔細觀察可發現3種更新格式的能量衰減速度存在差異，隱式情況下能量衰減最快。

3 結論和討論

數值模擬表明，使用復頻移拉伸坐標算子的ADE－PML比使用非復頻移拉伸算子（即傳統拉伸坐標算子）的ADE－PML更能有效消除高角度入射情況下的虛假反射。對ADE－PML輔助變量的3種更新格式的檢驗說明，3種格式在吸收效果上不存在明顯差異，但顯式條件下可以獲得相對較好的吸收效果；長時間的能量衰減計算表明，3種更新格式條件下的ADE－PML都穩定至2×105時間步，說明ADE－PML在數值模擬中具有長時間穩定性。由于ADE－PML技術具有非分裂場格式，降低了編程難度，且由于適應高階精度時間格式，可以進一步推廣到波動方程高精度偏移成像中。

（Reference）：

［1］Clayton R，Engquist B.Absorbing Boundary Conditions for Acoustic and Elastic Wave Equations［J］.Bulletin of the Seismological Society of America，1977，67（6）：1529－1540.

［2］Liao Z P，Wong H L，Yang B P，et al.A Transmitting Boundary for Transient Wave Analysis［J］.Scientia Sinica，1984，27（10）：1063－1076.

［3］Higdon R.Absorbing Boundary Conditions for Difference Approximations to the Multidimensional Wave Equation［J］.Mathematics of Computation，1986，47（176）：437－459.

［4］Bérenger J P.A Perfectly Matched Layer for the Absorption of Electromagnetic Waves［J］.Journal of Computational Physics，1994，114（2）：185－200.

［5］Chew W C，Weedon W H.A 3－D Perfectly Matched Medium from Modified Maxwell’s Equations with Stretched Coordinates［J］.Microwave and Optical Technology Letters，1994，7（13）：599－604.

［6］Drossaert F H，Giannopoulos A.A Nonsplit Complex Frequency Shifted PML Based on Recursive Integration for FDTD Modeling of Elastic Waves［J］.Geophysics，2007，72（2）：9－17.

［7］Komatitsch D，Martin R.An Unsplit Convolutional Perfectly Matched Layer Improved at Grazing Incidence for the Seismic Wave Equation［J］.Geophysics，2007，72（5）：155－167.

［8］Ramadan O.Auxiliary Differential Equation Formulation：An Efficient Implementation of the Perfectly Matched Layer［J］.IEEE Microwave and Wireless Components Letters，2003，13（2）：69－71.

［9］Moerloose J D，Stuchly M A.Behavior of Berenger’s ABC for Evanescent Waves［J］.IEEE Microwave and Wireless Components Letters，1995，5（10）：344－346.

［10］Moerloose J D，Stuchly M A.Reflection Analysis of PML ABC’s for Low－Frequency Applications［J］.IEEE Microwave and Guided Wave Letters，1996，6（4）：177－179.

［11］Kuzuoglu M，Mittra R.Frequency Dependence of the Constitutive Parameters of Causal Perfectly Matched Anisotropic Absorbers［J］.IEEE Microwave and Guided Wave Letters，1996，6（12）：447－449.

［12］Collino F，Tsogka C.Application of the PML Absorbing Layer Model to the Linear Elastodynamic Problem in Anisotropic Heterogeneous Media［J］.Geophysics，2001，66（1）：294－307.

［13］Festa G，Vilotte J P.The Newmark Scheme as Velocity－Stress Time－Staggering：An Efficient PML Implementation for Spectral－Element Simulations of Elastodynamics［J］.Geophysical Journal International，2005，161（3）：789－812.

［14］Zhang W，Shen Y.Unsplit Complex Frequency－Shifted PML Implementation Using Auxiliary Differential Equations for Seismic Wave Modeling［J］.Geophysics，2010，75（4）：T141－T154.

［15］周輝，謝春臨，王尚旭，等.復雜地表地震資料疊前深度偏移成像［J］.吉林大學學報：地球科學版，2012，42（1）：262－268.Zhou Hui，Xie Chunlin，Wang Shangxu，et al.Prestack Depth Migration for Geological Structures with Complicated Surface［J］.Journal of Jilin University：Earth Science Edition，2012，42（1）：262－268.

［16］孟慶生，樊玉清，張珂，等.高階有限差分法管波傳播數值模擬［J］.吉林大學學報：地球科學版，2011，41（1）：292－298.Meng Qingsheng，Fan Yuqing，Zhang Ke，et al.Tube Wave Propagation Numerical Simulation Based on High Order Finite－Difference Method［J］.Journal of Jilin University：Earth Science Edition，2011，41（1）：292－298.