多組數據方差分析模型：以殺蟲劑藥效為例

陳 維

(天津職業技術師范大學，中國 天津300222)

0 前言

在試驗法研究調查中，我們常常采取最傳統的方法，分為試驗組和對照組兩組進行研究。然而，在實際生活中由于研究問題的復雜性，往往需要研究多于兩組的研究對象之間的差異，其中多組數據位置的比較就是最基本的問題，我們正是通過方差分析來解決這一問題。在參數統計中，常常需要數據符合正態分布假定[1-3]，但是，當先驗信息不滿足或者不足以支持正態分布時，就要采取非參數方法解決。

1 方差分析法的說明

根據試驗設計的不同，我們采取不同的方差分析方法

1.1 完全隨機設計

當影響因素只有一個時，如例1，分析這樣的數據的方法就叫做單因素方差分析，這是最簡單的實驗設計。

例1：對三個工廠生產的燈泡進行壽命測試，每品牌隨機試驗，結果得如下數據（單位：天）

表1

完全隨機設計必須具備的兩個條件：

（1）試驗材料（材質，地質，動植物）是同質

（2）每種處理（溫度，照明）要隨機安排試驗材料

假設檢驗H0∶μ1=μ2=μ3H1∶?i，j，i≠j，i，j=1，2，3，μi≠μj（至少有一種處理的均值不等）

1.2 完全隨機區組設計

假設需要對A,B,C三種處理的車（在這里三種處理就相當于三種品牌，車包括自行車，摩托車和汽車）油耗設計比較試驗，每種處理方法重復觀測5次。也就是說，將15輛車分為五組，每組三輛，分別接受三種不同的處理，共生成3×5=15份報告，供三種處理方法進行比較。而實際中，我們知道，由于每輛車自身的不同，油耗的差異可能比較大，若剛好油耗少的分配到較好的處理方法，而油耗大的分配到較差的處理方法，結果可能測不到哪種處理方法更好。這是由于在該實驗中，不同的車自身構成除了處理之外的另一個因素，稱為區組。如果只取汽車，這就是完全隨機區組設計，如例2，其中汽車為區組。

例2：下表是世界三大汽車公司的五種不同的車型某年產品的油耗

表2

完全區組的實驗設計的需具備的條件：

（1）試驗材料不同應根據需要分成幾組，幾個性質相近的實驗單位為一區組，從而減小區組內個體差異，增大區組間差異。

（2）每個區組內的試驗個體隨機的全部參加各種處理。

（3）每個區組內的試驗數等于處理數。

假設檢驗H0∶μ1=μ2=μ3H1∶μi≠ μj，?i，j

1.3 均衡的不完全區組設計

因為不能保證每個區組都有對應的樣本出現，這就產生了不完全區組設計。如處理組很大，但同一組的樣本數又不允許太大，在一個區組中可能不能完全包含所有的處理，則只能在一個區組內安排部分處理，也就是說不是所有區組的處理都被用于各組的試驗中[4]，稱這種區組設計為不完全區組設計，其中最常用的就是均衡不完全區組設計。

均衡區組設計，記為BIB（k，b，r，t，λ），需具備以下條件：

（1）在同一區組中每個處理最多出現一次。

（2）每個區組的樣本數為t，t小于處理個數k。

（3）每個處理出現在同樣多的r個區組中。即：b≥r或kffgt;t

（4）在同一區組中，每兩個區組相遇次數一樣（λ次）。

即：（1）kr=bt

（2）λ(k-1)=r(t-1) （1.1）

（3）b≥r或kffgt;t

特別的：t=k,r=b,則為完全隨機區組設計

2 方差分析的檢驗方法

2.1 Cochran檢驗

對于一個完全區組設計，如果觀測值只有“是”或“否”，“同意”或“不同意”，“1”或“0”等等，這些二元定性數據。因為重復的數據太多，秩方法受到了限制，這就要使用Q檢驗法，來分析多數據之間的差異是否存在。

假設有k個處理和m個區組，樣本為計數數據，如表3。

假設檢驗

H0：k個總體分布相同（或各處理發生概率相等）

H1：k個總體分布不相同（或各處理發生概率不相等）

表3

分析：

n.j為第j個處理中1的個數，即之間的差異可以顯示出各個處理之間的差異。ni.為每一個區組中1的個數表示每格成功概率。

H0成立時，每一區組i內的成功概率Pi，j相等，對?j=1,2,…,k,?I,Pi1=Pi2=…=Pik=Pi.,nij服從兩點分布b(1,Pi.)。

一般n.j之間并非相互獨立，但是當n.j足夠大時，認為n.j近似獨立，得到自由度為v=k-1的近似χ2分布，即Cochran值為

結論：當檢驗統計量的值Q＜χ2

0.05，k-1，不能拒絕H0，反之接受H1。

2.2 Durbin不完全區組分析法

由前面提到，數據組很大，但是區組允許的樣本量有限，一個區組中很難包含所有處理。較常見的就是BIB設計，這里我們介紹一種秩檢驗，能夠應用于均衡不完全區組設計。

分析：

Xij表示第j個處理第i個區組中的觀測值，Rij為第i個區組中第j個處理的秩，Ri.=Rij，i=1,2,…,b。

H0成立時,k個處理的秩和非常接近，反之，當某處理效應大時，秩和與總體平均之間的差異也較大，于是統計量為

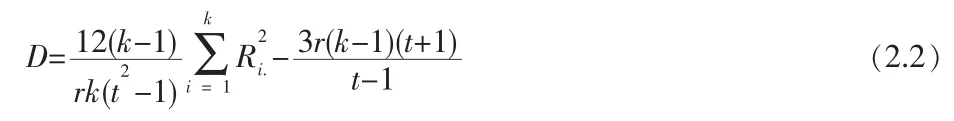
結論：對于顯著性水平α，如果D很大，比如大于或等于D1-α，D1-α為最小滿足PH0(D≥D1-α)=α的值，就可以拒絕零假設。在零假設下，對于固定的k和t，當r→∞時，D→χ2(k-1)。

3 實際應用

試驗一：現有A,B,C,D四種殺蟲劑，在南方四個地區試用，由于試驗用蚊子不足，故每種藥劑只能使用于三個地方，每一次試驗使用400只蚊子，其死亡數如下。如何檢驗四種藥劑的藥效是否不同？

表4

分析數據：得到下表，括號內的數，為各組內按4種處理觀測值大小。

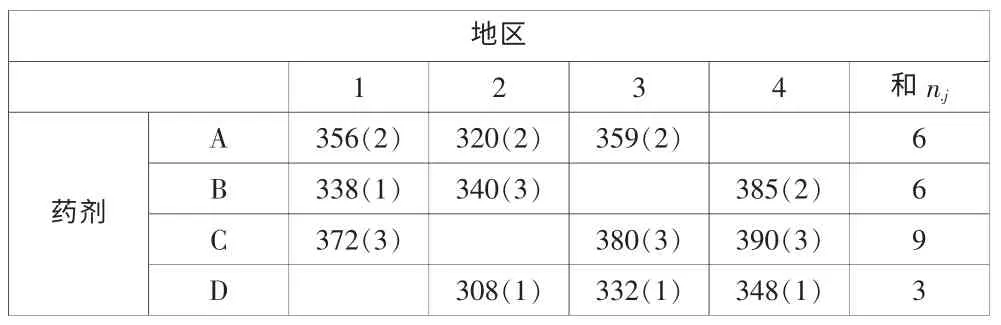
表5

假設檢驗問題為

H0：四種藥劑的藥效相同

H1：四種藥劑的藥效不同

統計分析：

t=3,k=4,r=3,自由度v=4-1=3，由（1.1）可知此設計為不完全區組設計。要采用Durbin不完全區組分析法，由（2.2）則：

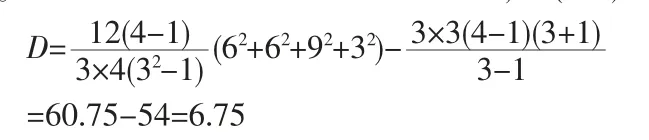
結論：實際測得D=6.75＜χ20.05，3=7.82，不能拒絕H0，沒有明顯的跡象表明四種藥劑藥效之間存在差異。

實驗二：為了考察其中三種殺蟲劑的殺蟲能力，又設計了一個實驗[5]，選取12位使用者，對產品投票，若使用者認為滿意，則給1分，否則給0分，所得結果如下，分析三種產品效果是否相同。

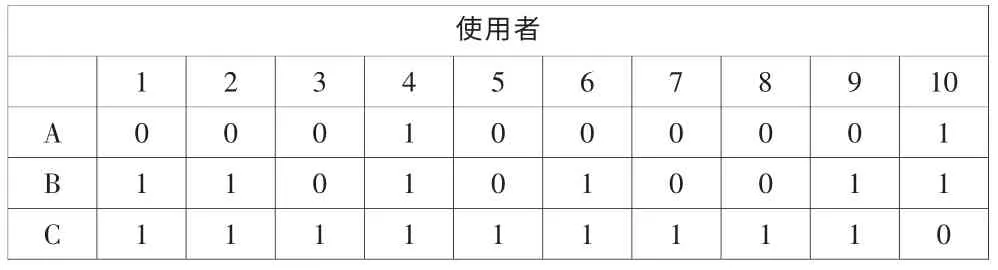
表6

分析數據，得到下表，分別求出每一區組，和每種處理的得分和

表7

假設檢驗問題為

H0：三種產品滿意程度相同

H1：三種產品滿意程度不同

統計分析：

由于各使用者每人殺蟲的手法和使用習慣的不同，對藥劑的殺蟲效果也有差異，故應以使用者為區組，由（2.1），則

結論：實際測得Q=8.2222＞χ20.05，2=5.991，接受H1，表明三種殺蟲劑滿意程度不同，即表明三種藥劑殺蟲效果不同，C比較受歡迎。

實際上，我們也可以計算一下三種藥劑的概率點估計

由計算可得p^.,1=0.12，p^.,2=0.35，p^.,3=0.53也支持了這一結論。

通過以上兩種試驗設計，第一組試驗并沒有表明四種藥劑的藥效區別，依然無法決策。而第二組試驗，則分析出了其中三種之中C產品的滿意度最好，即藥效最好，這就方便了我們做決策。同樣的道理，我們還可以分別將三種藥劑進行試驗，最終得到四種藥劑中效果最好的產品。

［1］Rice J.Mathematical Statistics and Date Analysis[M].3rd ed.Boston:Duxbury Press India 2007：22-57.

［2］Vapnik V N.Statistical Learning Theory[M].New York:Wiley-Interscience 1998：8-27.

［3］張堯庭.高等數理統計[M].北京:北京大學出版社，1998：4-34.

［4］劉勤，金丕煥.分類數據的統計分析及SAS編程[M].上海:復旦大學出版社，2002：57-75.

［5］David Hand，等.數據挖掘原理[M].張銀奎，等，譯.北京:機械工業出版社，2003：173-183.