求方陣初等因子的一種新方法及其數值實現

杜翠真，尹瀟瀟

（1.淮北師范大學 數學科學學院，安徽 淮北 235000；2.云南財經大學 統計與數學學院，云南 昆明 650221）

0 引言

矩陣理論的相當一部分內容都能看作是Jordan標準形的應用，所以Jordan標準形的求法受到了國內外學者的關注.利用λ-矩陣的初等變換化A的特征矩陣為標準形或對角形，再計算初等因子，或根據行列式因子、不變因子和初等因子的關系計算初等因子是求Jordan標準形常用的方法，如文獻[1].而對階數較高的矩陣，文獻[1]給出的方法計算量很大.

鑒于此，本文先求出冪零矩陣A的初等因子λj的個數hj，再利用n階矩陣A的特征值λi的秩指數求出A的初等因子(λ-λi)j的個數 hj(i=1,2,…,s).

1 基礎知識

定義 1.1[2]設A∈Cn×n，若存在正整數 k，使得Ak=0.稱A是冪零矩陣.滿足等式Ak=0的最小正整數k稱為A的冪零指數.

定義 1.2 設 A∈Cn×n，λi是 A的特征值(i=1,2,…,s)，若 r((λiE-A)ki)=r((λiE-A)ki+1)，則稱 ki是 A的特征值 λi(i=1,2,…,s)的秩指數.

引理1.1[1]每個n級復數矩陣A都與一個若當形矩陣J相似，這個若當形矩陣除去其中若當塊的排列次序外是被矩陣A唯一確定的，J稱為A的若當標準形.

即對任意 A∈Cn×n，則存在可逆矩陣 P∈Cn×n，使得

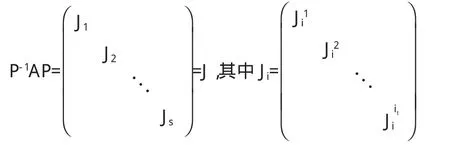
Jij是主對角線元素均是λi的若當塊(j=1,2,…,it).

若當形矩陣J是對角形矩陣的區別在于它的下對角線（與主對角線平行的下方第一條對角線）的元素是1或是0，因此 是一個特殊的下三角形矩陣.

2 主要結論

引理2.1 設A是冪零矩陣，那么r(A)>r(A2)>r(A3)>…>r(Ak)=r(Ak+1)=0.

證明 由引理1.1可知，對冪零矩陣A，存在可逆矩陣P，使得

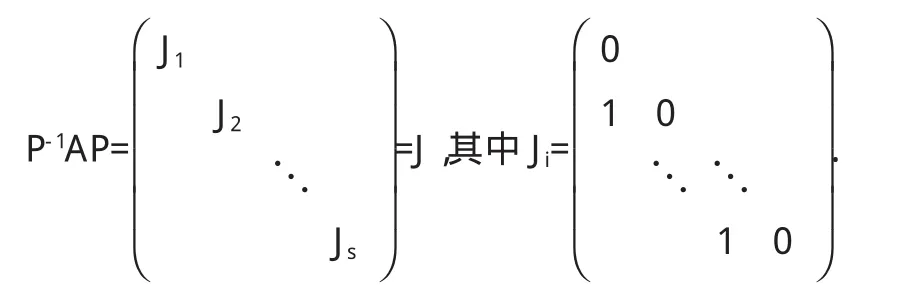
因為r(J)>r(J2)>r(J3)>…>r(Jk)=r(jk+1)=0，

r(Ji)=r(Ai)(i=1,2,…)，

所以r(A)>r(A2)>r(A3)>…>r(Ak)=r(Ak+1)=0.

引理2.2[3]對矩陣A,B,C，有r(ABC)>r(AB)+r(BC)-r(B).

因為r(A3)>r(A2)+r(A2)-r(A),r(A)-r(A2)>r(A2)-r(A3).

所以 △i=r(Ai)-r(Ai+1)(i=0,1,…,k-1)遞減，hi=△i-1-△i≥0(i=1,2,…,k).

對冪零指數為k的矩陣A，A的最后一個不便因子是λk，所以 A的初等因子為 λj(j∈{1,2,…,k})，且至少有一個初等因子λk.

定理2.1 設A是冪零指數為k的冪零矩陣，那么A有

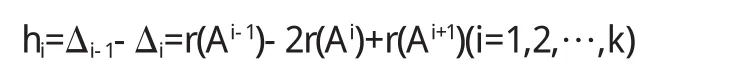
個初等因子λi.

證明 設A的Jordan標準形為J，存在可逆矩陣P，使得P-1AP=J.

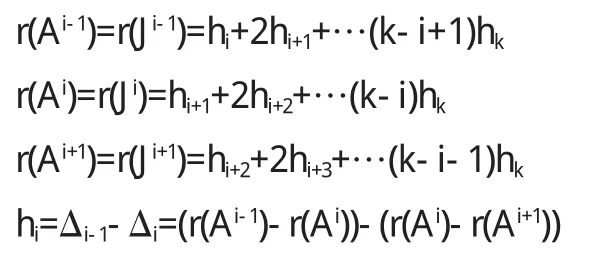
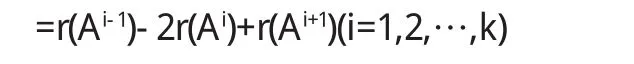
所以A有hi=r(Ai-1)-2r(Ai)+r(Ai+1)(i=1,2,…,k)個初等因子

定理 2.2 設 A∈n×n，λi(i=1,2,…,s)是 A的特征值，那么

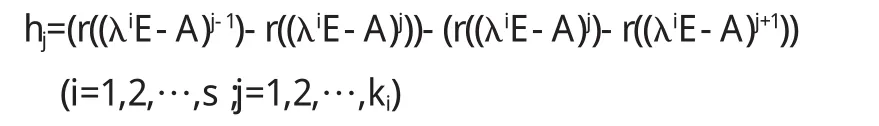
為A的初等因子(λ-λi)j個數，若λi為單根，那么A的初等因子(λ-λi)的個數是 1.

證明 設A的Jordan標準形為J，存在可逆矩陣P，使得P-1AP=J.

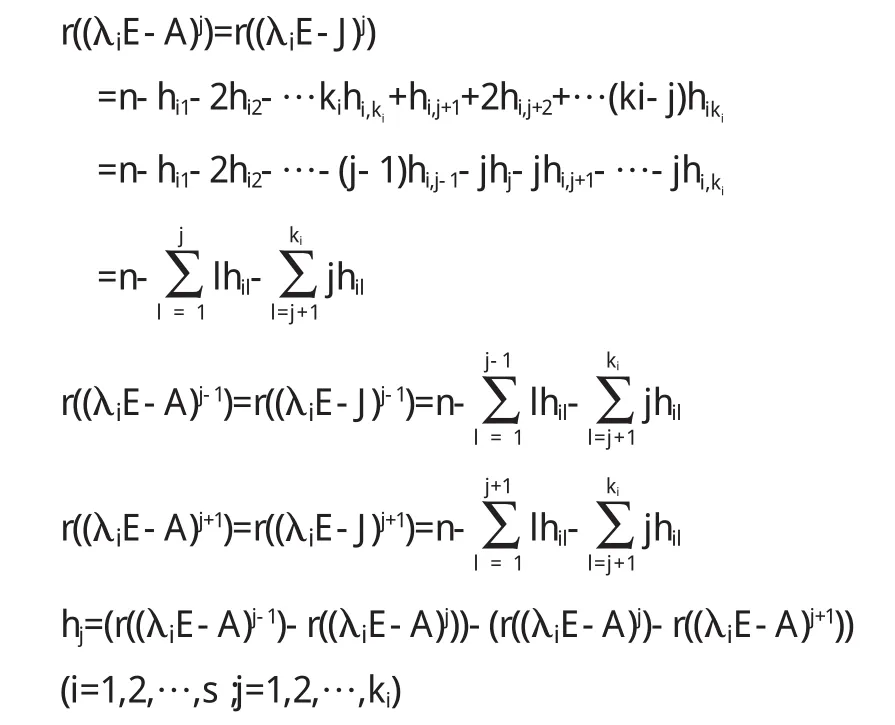
所以A有hj個初等因子(λ-λi)j.

3 應用舉例及其數值實現

由定理2.2可知，對任意一個n階矩陣A，按照定理2.2中的公式可唯一求出A的初等因子(λ-λi)j的個數hj.下面給出實例及其Matlab程序實現.

解 |λE-A|=(λ-1)2(λ+1)，所以 λ1=1(2重）,λ2=-1.

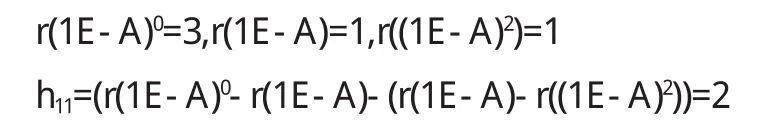
所以A的初等因子為λ-1,λ-1,λ+1.

Matlab編程如下

4 結論

本文利用矩陣A的特征值λi的秩指數給出初等因子(λ-λi)j的個數，避開繁瑣的λ-矩陣的初等變換，化A的特征矩陣為對角形，求出初等因子.該方法降低了計算難度和計算量，簡單易行，程序性強，易于編程.

〔1〕北京大學數學系幾何與代數教研室代數小組.高等代數[M].第三版.北京:高等教育出版社,2003.

〔2〕張禾瑞,郝炳新.高等代數[M].第四版.北京:高等教育出版社,2007.

〔3〕趙禮峰.高等代數解題法[M].合肥:安徽大學出版社,2004.