一種風險型決策的效用模型及其應用
毛春華
(湖南財政經濟學院,湖南 長沙 410205)
0 引言
風險型決策的最基本的決策準則是期望值準則,其基本原理是決策者應該選擇行動空間中期望值最大的行動.期望值準則也是最直觀處理風險決策的方法,但它不是一個很合理的準則,像著名的Petersburg悖論指出的那樣,利用期望值準則可以導致不理性的決策.為解決Petersburg悖論,Bernouli在1738年提出了效用函數的概念并論述效用函數的可能形式.但是,期望效用理論在其形成與發展過程中,也遇到了一些新的挑戰.最大期望效用準則在某些實際問題中顯示出了偏差.如在1952年,法國數學家、諾貝爾經濟獎獲得者Allias就提出了著名的悖論.本文試圖引進決策行動的風險,和期望效用一起作為另一個決策變量,在作出決策行動時綜合考慮每一行動方案的期望效用與風險大小,該模型能很好地解釋決策悖論,是對期望效用理論的完善與發展.
1 模型的建立
風險型決策問題G=(Θ,A,u),每一決策行動對于決策人來說,既具有一定的期望效用,但也面臨一定的風險.所以,決策人在作出決策行動時,必須同時考慮以上兩個方面的因素.因此,我們把它們作為兩個決策變量,引入到同一個決策函數f[Eu,Hu]中.為此,我們首先構造一個評價決策行動優劣的決策函數f[Eu,Hu].
定義1 給出風險型決策問題G=(Θ,A,u),且行動空間中至少存在兩個行動方案,如果行動方案a∈A使存在,則行動a的效用決策函數定義為
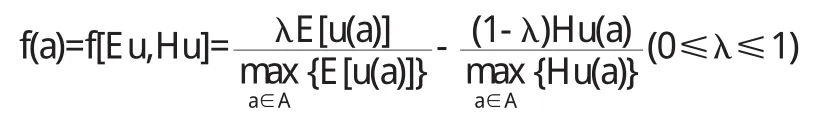
其中,E[u(a)]表示行動a的期望效用,Hu(a)表示行動a的效用風險熵,而λ表示決策者對于所面臨的決策問題的期望效用和風險大小的平衡系數,它隨著決策著的不同而不同,也隨著決策行動空間的變化而變化.不妨稱λ為決策行動的效用—風險平衡系數,一般來說,當決策者比較重視決策行動的期望效用而不重視風險大小時,λ接近于1,當λ=1時,則該決策函數就是決策行動的期望效用.反之,當決策者特別關注決策行動的風險時,λ相對較小.
顯然,該效用決策函數只是一個比較性定義,它只具有相對性的含義.由決策行動空間中的各個決策行動的期望效用和每個行動本身的效用風險熵決定,它既考慮了每一決策行動對決策者所具有的主觀期望效用,也考慮了每一行動所具有的不確定性大小給決策者帶來的效用風險.
定義2 風險型決策問題(Θ,A,u),a1,a2∈A,如果f(a1)>f(a2),則我們稱行動 a1優于 a2,即 f(a1)>f(a2)圳a1>a2.
如果存在行動a*∈A,使得,則稱行動方案a*為在效用決策模型下的最優方案.
利用效用模型的決策方法可以將行動空間中的每一行動方案按其函數值的大小進行排序,從而找出其中的最優方案.
2 模型的性質
定義1風險型決策的效用模型有如下一些性質:
定理1 決策函數f[Eu,Hu]是關于期望效用E[u(a)]的增函數,是關于效用風險熵Hu(a)的減函數.且對于a1,a2∈A,如果有
E[u(a1)]≥E[u(a2)],且 Hu(a1)≤Hu(a2),則 f(a1)≥f(a2).
證明 由定義1中效用決策函數表達式

容易得出結論.
定理2 對于風險型決策問題(Θ,A,u),有
(1)若決策行動A中的所有行動方案的期望效用E[u(a)]都相同,則效用風險熵Hu(a)最小的行動是最優行動.
(2)決策行動A中的所有行動方案對應的效用風險熵Hu(a)都相同,則期望效用E[u(a)]最大的行動即為最優行動.
證明 因為每一決策行動的期望效用E[u(a)]都相同,決策函數f[Eu,Hu]是關于效用風險熵Hu(a)的減函數,從而效用風險熵最小的行動決策函數值最大,根據定義2,它是最優行動.
同理,若每一決策行動效用風險熵Hu(a)相同,決策函數是關于期望效用E[u(a)]的增函數,從而期望效用E[u(a)]最大的行動決策函數值也最大,即它是最優行動.
由以上可知,若所有決策行動的期望效用E[u(a)]相同,則只要比較它們的效用風險熵Hu(a)的大小即可,效用風險熵最小的即為最優行動;如果所有行動方案的效用風險熵Hu(a)的相同,則只要比較它們的期望效用E[u(a),期望效用最大的即為最優行動.特別地,我們有:
定理3 對于風險型決策問題(Θ,A,u),當行動空間中只有行動a1和a2時,若行動方案a1和a2的期望效用E[u(a)]相同,則效用風險熵Hu(a)小的行動即為最優行動;如果它們的效用風險熵Hu(a)相同,則期望效用E[u(a)]大的即為最優行動.
更進一步,如果兩個決策行動a1和a2中,a1是確定性行動,a2為風險行動,則還有如下結論:
定理4(1)若兩行動a1和a2有相同的期望效用E[u(a)],則確定性行動a1即為最優行動.(2)若兩行動有相同的均值,假設決策者是風險厭惡型的,則確定性行動a1為最優行動.
證明 (1)很顯然,由效用風險熵的性質可知Hu(a1)=0,Hu(a2)>0,且它們的期望效用值E[u(a)]相同,根據定理2,有f(a1)>f(a2),即a1為最優行動.
(2)設風險型行動a2的概率分布為

表1 風險行動a2的概率分布
令a1和a2的期望值為c,由于決策者為風險厭惡型的,于是其效用函數局部為上凸的,由Jesen不等式,可以得到
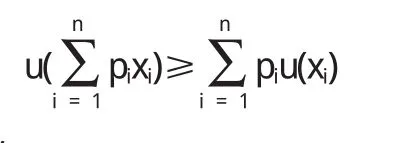
于是有

行動a1和a2的效用風險熵有Hu(x,a1)=0,Hu(x,a2)>0,因而,根據定理3有f(a1)>f(a2),即a1為最優行動.
對于如上的決策問題,如果用期望效用準則來進行決策,同樣可以得出行動a1優于行動a2.即對于該決策問題,用效用決策方法與期望效用理論得到的結果相一致.由此可見,在某些情況下,兩個準則得到的結論是相容的.同時,上述定理得到的結論與一個風險厭惡型的決策者憑直覺作出的決策一致.由此也可以說明,對于該決策問題,效用—風險決策模型既可以作為決策的規范化模型,也可以作為決策的描述性模型.
如果決策者為風險中性的,我們還有如下的結論:
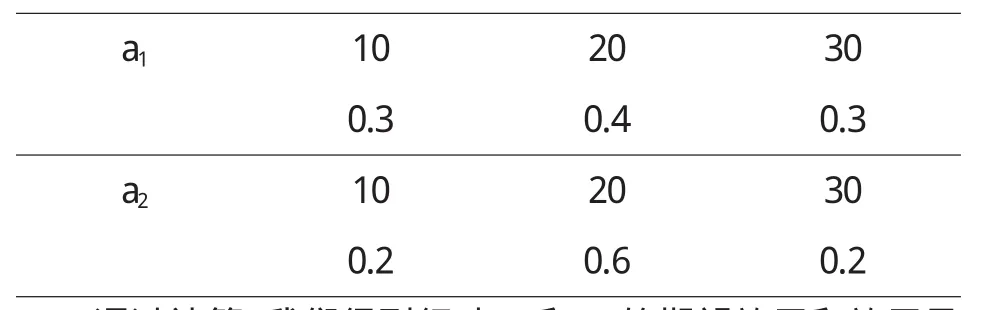
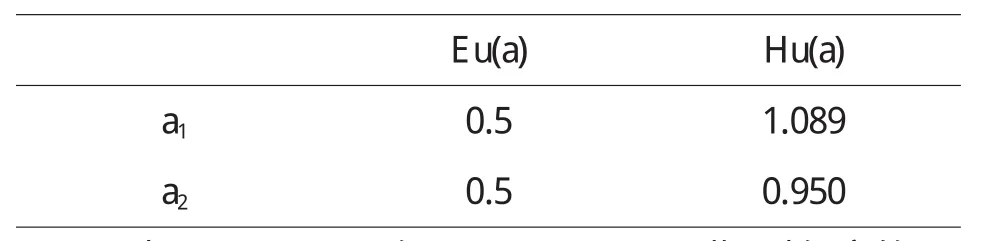
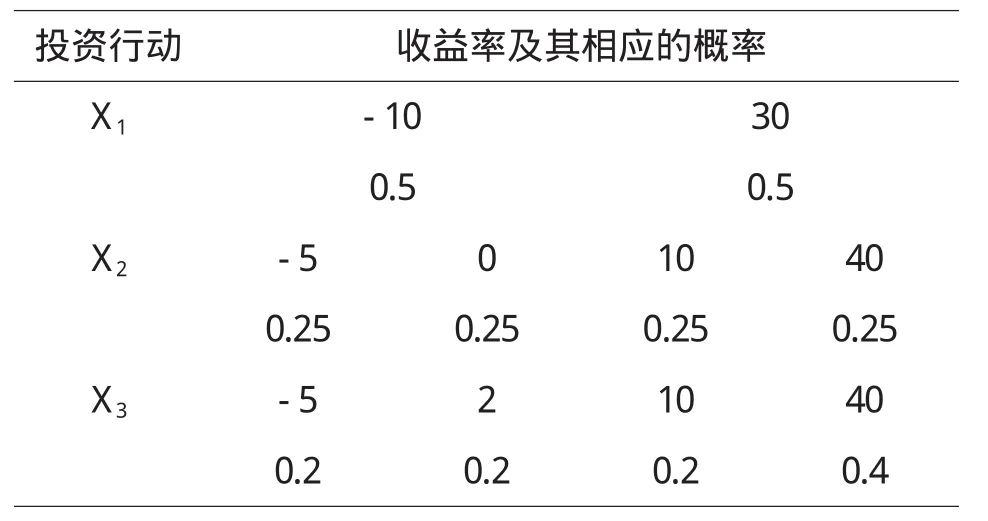
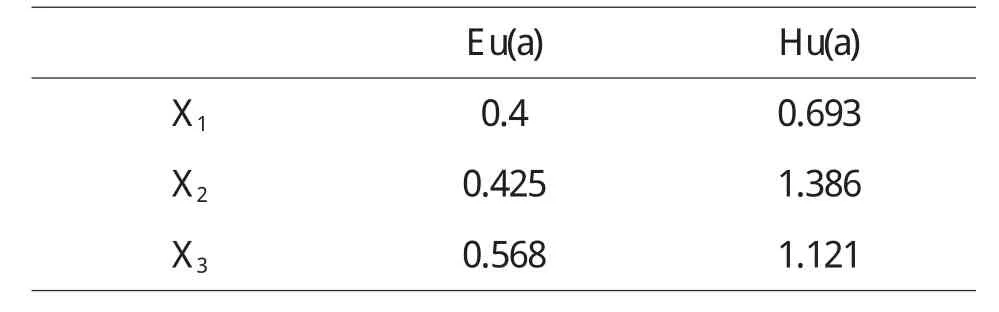
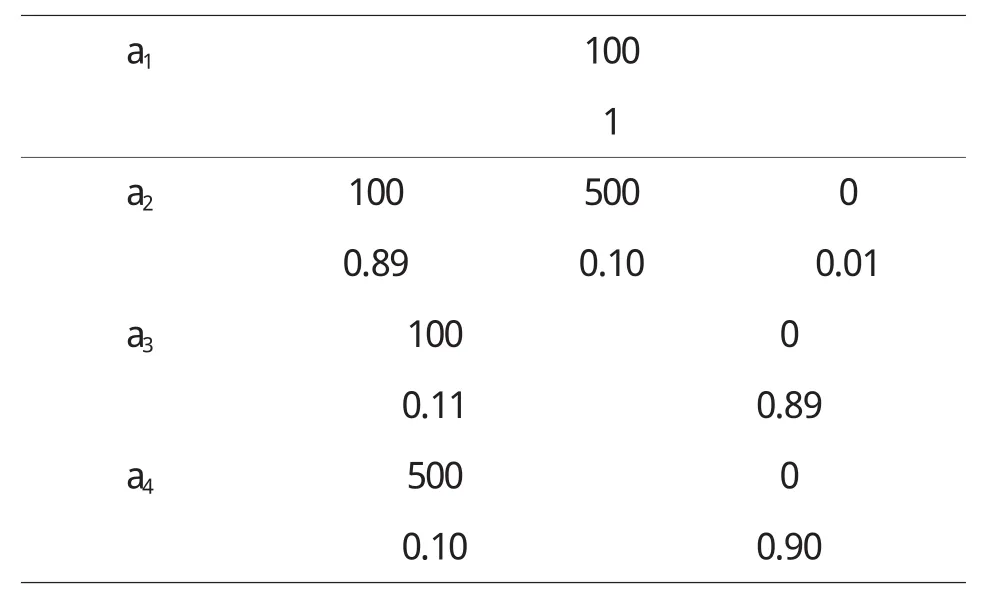
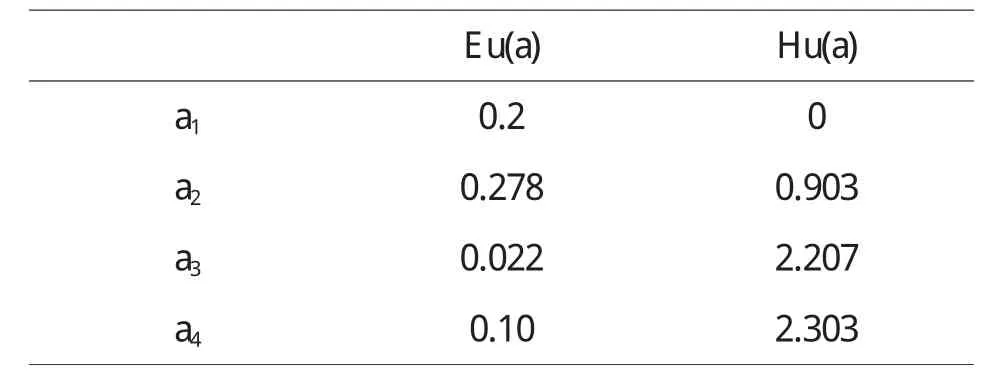
定理5 對于風險型決策問題(Θ,A,u),假定決策者是風險中性的,具有線性的效用函數,設對于行動空間中的行動a1和a2具有相同的均值,即E[u(a1)]=E[u(a2)],如果Hu(x,a1) 證明 由于決策者具有線性的效用函數,且行動a1和a2有相同的期望值,從而它們有相同的期望效用,又Hu(x,a1) 在以下實例中,假設決策者是風險中性的(其它風險情形,模型的應用方法亦相同),有線性的效用函數u(x)=,其中xmax和xmin分別表示最大的和最小的損益值.例1 設風險型決策只有兩個行動a1和a2,它們分別如下 a1:以0.3的概率得到10元,以0.4的概率得到20元,以0.3的概率得到30元; a2:以0.2的概率得到10元,以0.6的概率得到20元,以0.2的概率得到30元.列表如下: 表2 風險型行動a1和a2的收益及其概率 通過計算,我們得到行動a1和a2的期望效用和效用風險熵于下表: 表3 行動a1和a2的期望效用和效用風險熵 因為 Eu(a1)=Eu(a2),但 Hu(a1)>Hu(a2),因此,對任意的 λ,由定理 3,都有 f(a1) 例2 現有三個風險型投資決策X1,X2,X3其收益率(%)及其相應的概率如下表所示 表4 風險投資行動X1,X2,X3 通過計算,我們可以得到三個行動X1,X2,X3的期望效用和效用風險熵,對其列表如下 表5 行動X1,X2,X3的期望效用和效用風險熵 很明顯,由于Eu(X3)>Eu(X2),且Hu(X3) 再來分析X3與X1,假設決策者的期望效用-效用風險熵平衡系數為λ,則X3與X1的效用函數值分別 X3優于X1的充要條件為 即當且僅當0.511<λ≤1時,投資者的決策行動X3優于X1.同理,我們可以討論X2與X1之間的優劣關系. 接下來我們進一步分析X1,X2,X3之間的隨機占優關系,不難得到它們的分布函數分別為 容易驗證,X1和X2之間,X1和X3之間不具有一階隨機占優關系,而對任何x,均有F3(x)≤F2(x),且至少存在一個x0,使得 F3(x0)≤F2(x0),于是 X3一階隨機占優于 X2,這與效用決策模型得到的結論一致. 例3 Allias悖論的解釋,Allias決策悖論的損益值及其相應的概率可列表如下: 表6 Allias悖論的決策行動 計算它們的期望效用和效用風險熵于下表: 表7 行動a1,a2,a3,a4的期望效用和效用風險熵 于是,它們的效用決策函數值分別為 由效用決策模型,我們有 利用本文構造的決策模型比較合理的解釋了Allias悖論,同時也可以看出,人的決策行為不只是考慮期望效用,其實還要考慮決策的風險因素,因此在解決風險型決策問題時,同時考慮期望效用和風險兩個因素更加科學,也更符合決策者的決策行為機理. 〔1〕陳廷.決策分析[M].北京:科學出版社,1987.70~78. 〔2〕姜青舫.現代效用理論 [M].貴州:貴州人民出版社,1990.15~24. 〔3〕張堯庭,陳慧玉.效用函數及優化[M].北京:科學出版社,2000.39~42. 〔4〕Bell,D.E,One-Switch Utility Function and a Measure of risk,Managent Science,1988(34):1416~1424. 〔5〕姜丹.效用風險熵[J].中國科學技術大學學報,1993,82(2):159~168.3 模型的應用
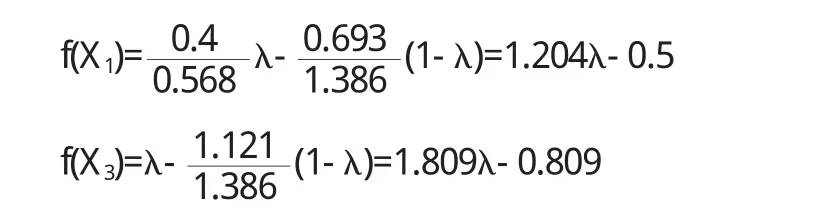
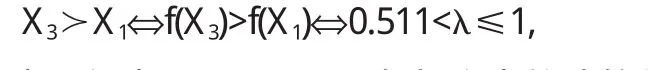
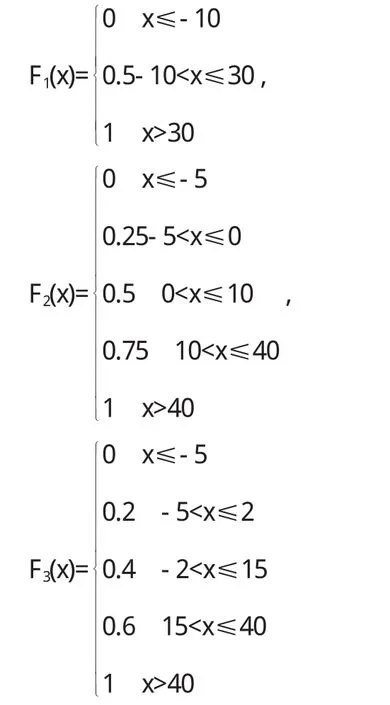
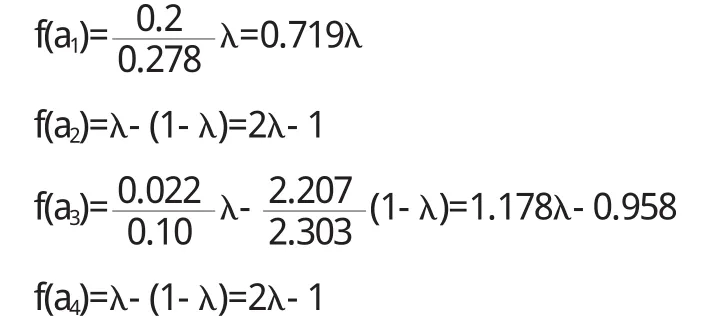
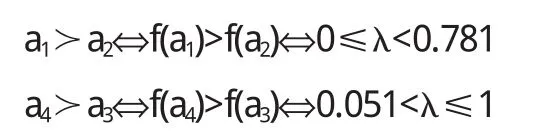
4 結束語

