帶三角形骨架加強結構機匣的剛度特性分析

洪宇，常宇博，肖雙強，廖華琳

(中國燃氣渦輪研究院，四川成都610500)

帶三角形骨架加強結構機匣的剛度特性分析

洪宇，常宇博，肖雙強，廖華琳

(中國燃氣渦輪研究院，四川成都610500)

對帶三角形骨架加強結構的航空發動機機匣的主要結構參數進行分析，以機匣質量和剛度作為目標函數，建立了研究的變量和約束條件，并采用相似準則將其無量綱化。采用均勻試驗設計方法生成樣本建立試驗組，并設立傳統板殼機匣作為對比組，分別開展有限元數值試驗。運用逐步回歸法分析試驗結果，形成了表征機匣剛度和質量的擬合公式，比較了該類機匣與傳統板殼機匣的剛度特性，給出了各主要結構參數對機匣剛度的影響規律。

航空發動機；機匣；骨架加強結構；剛度；回歸分析；數值試驗

1 引言

航空發動機機匣作為薄壁筒體，其剛度、強度、屈曲、振動等力學性能均較差，通常根據力學環境需要，設計相應的加強結構，增強其力學性能[1]。自20世紀80年代以來，以美國F119、F135和英國EJ200發動機為代表的先進戰斗機發動機，在外涵和加力筒體上大量應用帶三角形骨架加強結構的機匣(以下簡稱骨架機匣)。近年來，國內發動機制造行業開展的化學銑削工藝研究[2]，適用于該類結構的高效加工、制造，從而初步具備了在國內發動機上應用該結構的條件。

骨架機匣由一層較薄的機匣筒體和三角形分布的加強結構共同承擔載荷，一般認為其具有結構效率高、力學穩定性好等優勢。但由于其結構較傳統板殼機匣復雜，在機匣方案設計初期沒有形成可用于有限元分析的實體模型之前，難以準確預估其質量和剛度，從而影響機匣的設計效率，容易造成不必要的設計反復。為解決設計初期預估機匣剛度的問題，本研究探求該類機匣的剛度特性，及其主要結構參數對機匣剛度的影響，為參數選取提供依據。

2 研究內容與模型

由于機匣在工作中承受著內壓、彎剪、拉壓、扭轉等的聯合作用，故本研究重點考察機匣在抗拉、抗扭和抗彎三方面的特性。

骨架機匣結構形式復雜，設計參數眾多，難以得到剛度與結構參數之間的解析關系，且其解析關系呈現強烈的非線性。因此綜合文獻[3]、[4]中對復雜結構力學特性的分析方法，為尋找機匣剛度相對骨架結構參數的變化規律，分別建立機匣實體模型和有限元模型，得到數值分析結果。在計算數據基礎上，近似擬合得到機匣各結構參數對機匣抗拉、抗彎、抗扭剛度影響的數學關系，從而實現研究目標。

為簡化研究，選取圖1所示簡化后的機匣實體模型為研究對象，其具有結構與剛度都相同的安裝邊，進出口直徑一致，骨架均勻、無安裝座、線彈性，且各向同性。機匣的加強結構(筋梁)，可看作展開投影如圖2所示結構在機匣表面重復排列后的結果。機匣主要結構參數包括機匣內直徑D0、骨架區域長度l0、骨架單元周向分布數量Nr、骨架單元軸向分布數量Nx、筋梁厚度t、筋梁寬度d和筒體厚度h。

圖1 骨架機匣簡化模型Fig.1 The simplified model of the case with skeleton ribs

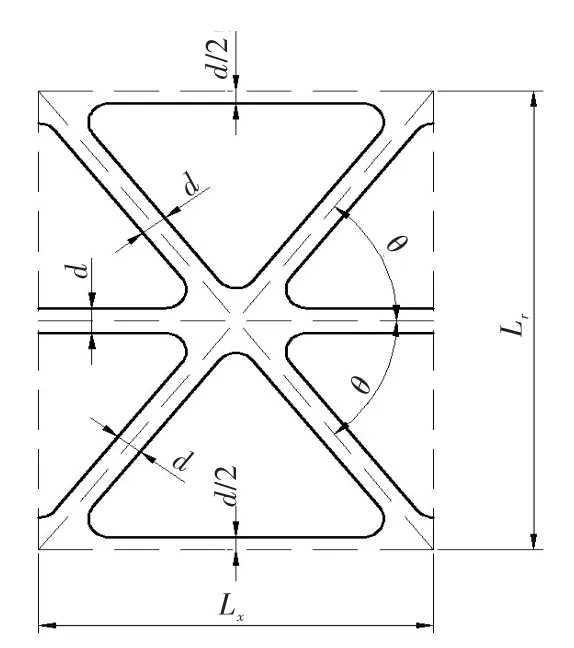
圖2 骨架單元投影Fig.2 The projection of a skeleton unit

為消除機匣尺寸影響，根據相似準則，對以上7個參數進行無量綱化，得到表征骨架區域形狀的6個無量綱參數：機匣長徑比x1，骨架單元軸向相對寬度x2，骨架方向角的正弦x3，筋梁相對厚度x4，相對寬度x5和機匣筒體厚度比x6。

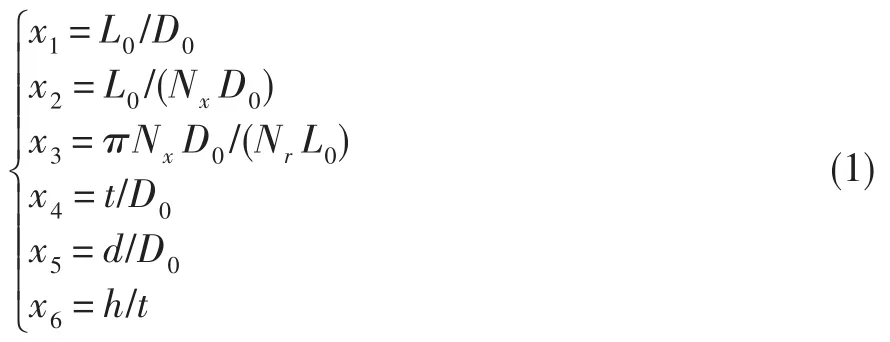
目標函數為機匣的抗拉剛度、抗彎剛度和抗扭剛度，為對比機匣質量影響，增加機匣骨架區域質量為另一個目標函數。無量綱化后，表征機匣骨架區域質量和剛度的參數，主要包括質量系數Rm、抗拉剛度系數RI、抗扭剛度系數RII和抗彎剛度系數RIII。

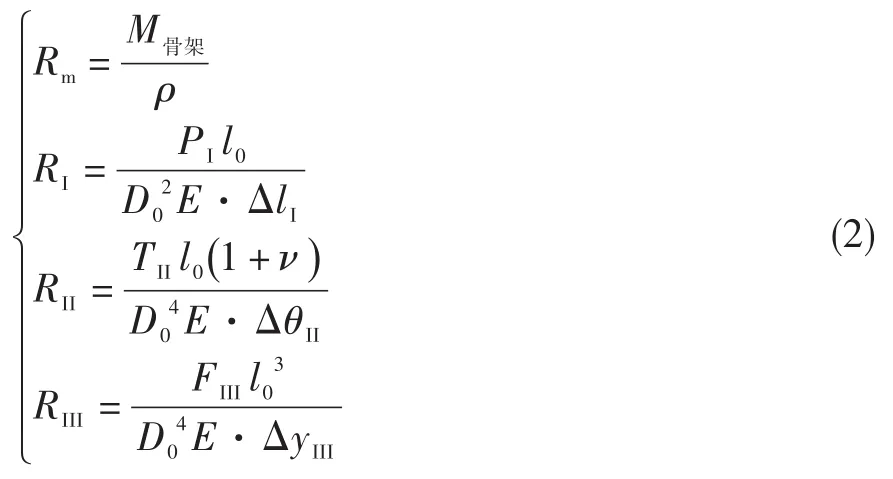
式中：ρ為機匣密度，E為機匣彈性模量，ν為機匣泊松比，PI為機匣承受的拉力，ΔlI為拉力作用下機匣的伸長量，TII為機匣承受的扭矩，ΔθII為扭矩作用下機匣的扭轉角，FIII為懸臂狀態下機匣自由端承受的剪切力，ΔyIII為剪切力作用下機匣自由端撓度。

3 樣本設計

運用均勻性試驗設計原則，以x1～x6為變量，開展試驗設計。根據6個變量在機匣設計中實際出現的范圍大小和頻次，分別按照4、6、8、6、6和6個參數水平，采用文獻[5]中方法，設計生成試驗樣本；然后剔除不滿足機匣設計邊界條件的樣本，最終得到用于數值分析的試驗組樣本共186個。

同時，為與板殼機匣對比分析，設置對比組樣本32個，由與試驗組樣本D0和l0對應相同但機匣厚度不同的機匣組成。

數值計算時，對所有試驗組樣本和對比組樣本，施加相同的軸向力、扭矩和剪切力，分別計算出各自的Rm、RI、RII和RIII。

4 結構建模與數值計算

按照圖3所示順序，對試驗組、對比組每個樣本進行結構建模和數值計算。計算中，統一選取ρ= 4 500 kg/m3，E=114 GPa，ν=0.3；固定模型機匣一端，在另一端分別施加PI=10 kN，TII=10 kN·m和FIII=10 kN，并記錄自由端變形量。

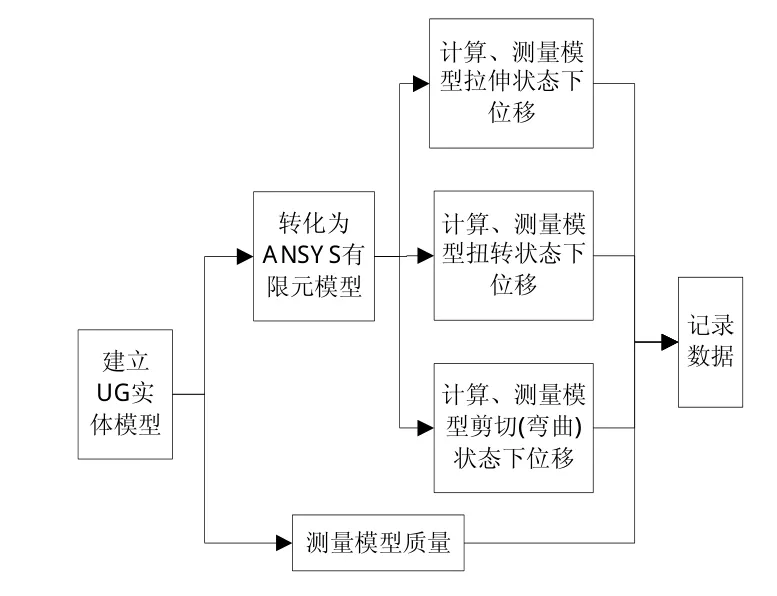
圖3 結構建模和數值計算的主要步驟Fig.3 The main process of structural and numerical modeling

以一模型機匣實體模型為例，其主要結構參數D0=308 mm，l0=96 mm，Nr=15，Nx=2，d=2 mm，t=2 mm，h=0.8 mm，則在有限元分析中，該實體模型在受拉(PI=10 kN)、受扭(TII=10 kN·m)和受剪(彎，FIII=10 kN)狀態下機匣位移分別如圖4～圖6所示。

根據數值計算結果無量綱化后，可得Rm=3.21× 10-3，RI=9.83×10-3，RII=1.21×10-3，RIII=1.71×10-3。

5 結果與分析

按照上述方法，完成試驗組和對比組所有樣本機匣計算，得到各自的Rm、RI、RII和RIII后，參考文獻[6]，運用分步回歸分析法進行擬合，得到Rm、RI、RII和RIII與各變量間的關系。分析可得，骨架機匣與等質量的板殼機匣相比，抗拉、抗彎、抗扭剛度均較差。各結構參數對機匣質量和剛度的影響為：①機匣長徑比與機匣質量近似成正比，機匣抗彎剛度隨長徑比的減小而急劇增大；②機匣筒體厚度比與機匣質量和抗拉、抗彎、抗扭剛度呈近似正比關系；③機匣質量、剛度與筋梁相對厚度或相對寬度的增加正相關，但斜率小于與筒體厚度比的關系；④骨架方向角不變時，骨架單元軸向相對寬度增加，機匣質量減小，骨架單元軸向相對寬度不變時，骨架方向角增加(骨架單元周向數量增加)，機匣質量先減小再增加。

常見機匣設計參數取值范圍中，與等質量板殼機匣相比，骨架機匣的相對抗拉剛度隨筋梁相對厚度的增加而降低，隨筋梁相對寬度的增加先降低后增加；相對抗扭剛度隨筋梁相對寬度的增加而降低；相對抗彎剛度隨筋梁相對厚度的增加而降低。

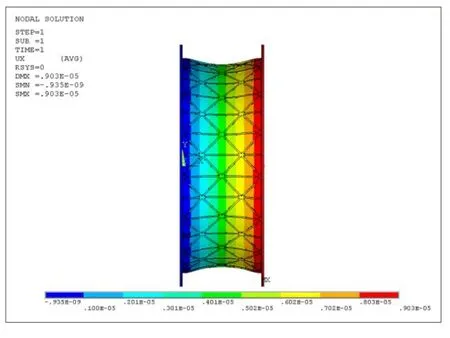
圖4 PI=10 kN下的機匣位移Fig.4 The case displacement atPI=10 kN

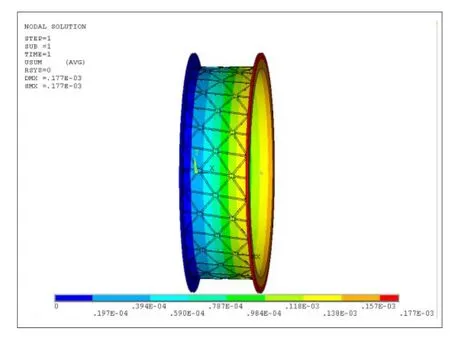
圖5 TII=10 kN·m下的機匣位移Fig.5 The case displacement atTII=10 kN·m

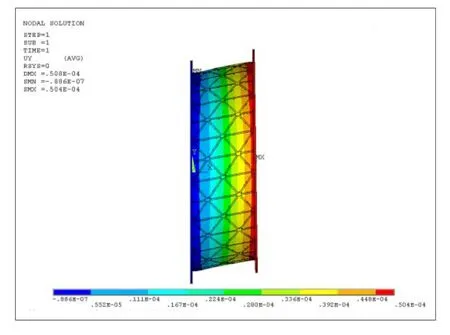
圖6 FIII=10 kN下的機匣位移Fig.6 The case displacement atFIII=10 kN

其他參數一定時，x2與x3中參數Nr、Nx等價。Nx一定時，Nr越小，骨架方向角越小，傾斜筋梁越接近軸向，機匣的抗拉剛度越好；Nr一定時，Nx越大，軸向單元數量增加，骨架傾斜角越大，抗拉剛度越好，如圖7所示。

骨架單元大小和形狀對機匣抗扭與抗彎剛度的影響如圖8、圖9所示。可見，Nr一定時，機匣抗扭、抗彎剛度隨Nx的增大而先增大后減小，在方向角為45°時達到最大值；Nx一定(單元長度一定)時，隨著Nr的增大，抗扭、抗彎剛度單調遞增，但在方向角小于45°時增長較快(斜率較大)，方向角大于45°后增長迅速放緩(斜率較小)。

常見機匣設計參數取值范圍中，與等質量板殼機匣相比，骨架機匣的相對抗拉剛度隨骨架方向角的減小而增大，在方向角接近0°時可與板殼機匣剛度一致；機匣方向角為45°時，相對抗扭剛度與相對抗彎剛度最大。

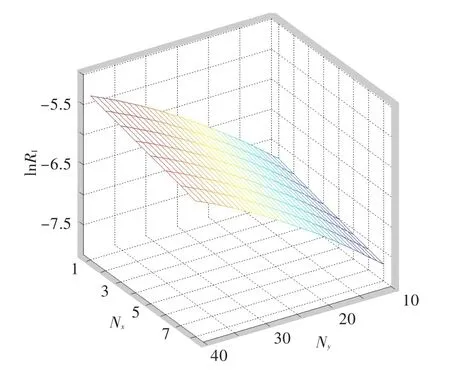
圖7 骨架單元大小和形狀對抗拉剛度的影響Fig.7 The effects of skeleton unit size and shape on the tensile stiffness

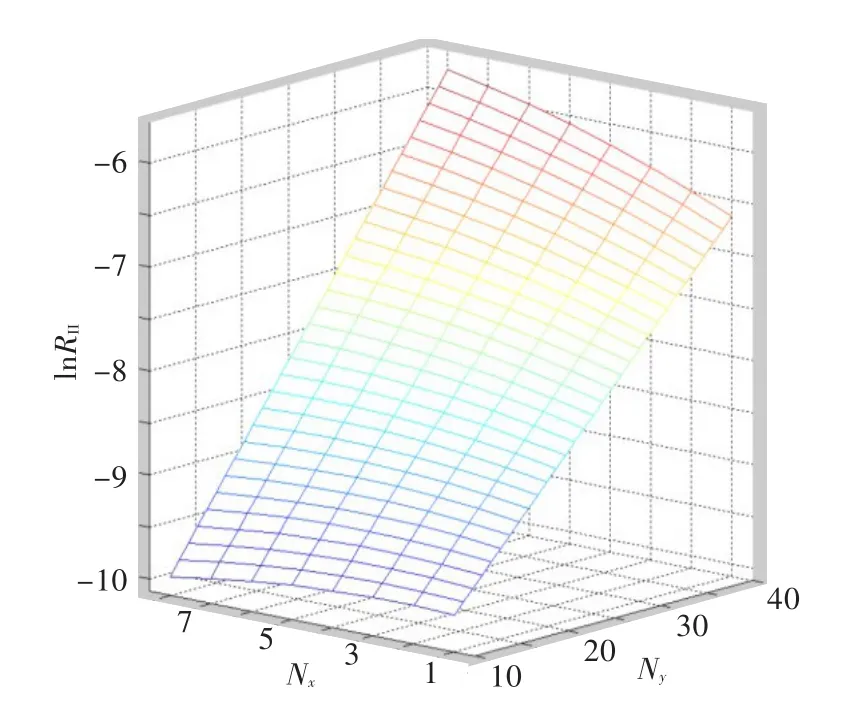
圖8 骨架單元大小和形狀對抗扭剛度的影響Fig.8 The effects of skeleton unit size and shape on the torsion stiffness

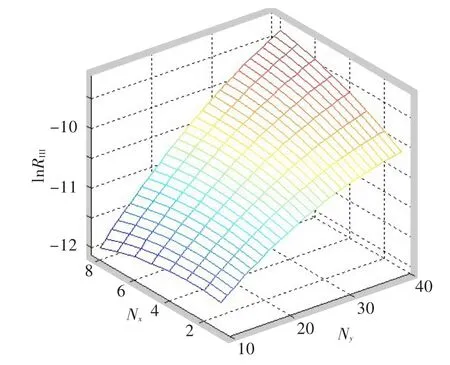
圖9 骨架單元大小和形狀對抗彎剛度的影響Fig.9 The effects of skeleton unit size and shape on the bending stiffness

6 結論

(1)在單一的簡單載荷(純拉力、扭矩和剪力載荷)條件下，與等質量的板殼機匣相比，帶三角形骨架加強結構機匣的整體剛度較差，僅在局部剛度增強上有優勢。長度和直徑相同時，帶三角形骨架加強結構機匣在抗拉、抗扭和抗彎剛度上，均低于同質量的板殼機匣。

(2)機匣剛度對筋梁厚度、寬度和密度的敏感性低于質量，所以排除工藝等因素，依靠增加筋梁截面積或筋梁密度提升剛度，不如增加筒體厚度效果明顯。

(3)筋梁方向角接近0°時，機匣的抗拉剛度最大；筋梁方向角為45°時，機匣的抗扭剛度和抗彎剛度最大。

(4)下一階段研究中，將進一步建立模型試驗件并開展相關試驗，對數值模型和計算結果進行驗證，并在此基礎上分析其他結構參數、機匣材料及制造工藝等因素對骨架機匣剛度的影響。

[1]張衛紅，章勝冬，高彤.薄壁結構的加強筋布局優化設計[J].航空學報，2009，30(11)：2126—2131.

[2]趙永崗，張春剛，王輝，等.化學銑切在鈦合金加工中的研究與應用[J].表面技術，2009，38(6)：83—86.

[3]謝永和，韋加礎.大型結構抗彎剛度優化設計研究[J].機械科學與技術，2009，28(2)：262—264.

[4]杜春江，錢林方，牟淑志.基于自適應參數的漸進結構優化方法[J].機械科學與技術，2009，28(1)：117—120.

[5]王巖，隋思漣.試驗設計與MATLAB數據分析[M].北京：清華大學出版社，2012：92—152，208—216.

[6]吳石林，張玘.誤差分析與數據處理[M].北京：清華大學出版社，2010：137—173.

Stiffness characteristic analysis of case with triangle skeleton ribs

HONG Yu，CHANG Yu-bo，XIAO Shuang-qiang，LIAO Hua-lin
(China Gas Turbine Establishment，Chengdu 610500，China)

The major structural parameters of aero-engine case with triangle skeleton ribs are analyzed. Taking the case mass and stiffness as objective functions,the variables and constraint conditions have been established,and made them dimensionless by using the similar criteria.The test group was built with de?signing samples from uniform design experiments.Taking the traditional plate shell case as the comparison group,the FEM numerical experiments are carried out for the two groups.The experimental results are ana?lyzed using the stepwise regression method,and the fitting formula to represent the mass and stiffness of case is gained.The comparison for the stiffness characteristics between the case with triangle skeleton ribs and the traditional plate shell case is made,and the influence of each structural parameter on the case stiff?ness is given.

aero-engine；case；skeleton ribs；stiffness；regression analysis；numerical experiment

V231.9

A

1672-2620(2016)01-0017-04

2014-05-19；

2014-11-19

洪宇(1990-)，男，四川廣安人，助理工程師，主要從事航空發動機總體結構設計技術研究。