基于參數(shù)敏感性的渦輪平面葉柵多目標(biāo)優(yōu)化設(shè)計(jì)

賴巍，李劍白，張劍

(中國(guó)燃?xì)鉁u輪研究院，四川成都610500)

基于參數(shù)敏感性的渦輪平面葉柵多目標(biāo)優(yōu)化設(shè)計(jì)

賴巍，李劍白，張劍

(中國(guó)燃?xì)鉁u輪研究院，四川成都610500)

渦輪葉片平面葉柵優(yōu)化方法借鑒已有研究成果，綜合考慮了造型方法、性能評(píng)估方法、優(yōu)化方法三個(gè)關(guān)鍵環(huán)節(jié)，在iSIGHT平臺(tái)下完成了葉柵優(yōu)化過(guò)程集成，建立了適合工程應(yīng)用的渦輪葉柵多目標(biāo)優(yōu)化設(shè)計(jì)系統(tǒng)。以高壓渦輪導(dǎo)葉中截面為例，從參數(shù)敏感性、反設(shè)計(jì)及多目標(biāo)優(yōu)化三個(gè)方面，對(duì)優(yōu)化方法進(jìn)行了較為深入的分析。結(jié)果表明，該方法可快速有效地優(yōu)化渦輪葉柵流場(chǎng)和性能。

渦輪葉片；參數(shù)敏感性；反設(shè)計(jì)；多目標(biāo)優(yōu)化；優(yōu)化算法；工程應(yīng)用

1 引言

傳統(tǒng)的渦輪葉片平面葉柵設(shè)計(jì)，首先根據(jù)初始葉片進(jìn)行流場(chǎng)計(jì)算，分析計(jì)算結(jié)果，然后按照經(jīng)驗(yàn)修改葉型設(shè)計(jì)參數(shù)，不斷重復(fù)該過(guò)程，直至得到滿意葉型，故其設(shè)計(jì)周期長(zhǎng)、工作量大。近年來(lái)，平面葉柵設(shè)計(jì)借助數(shù)值優(yōu)化方法大大縮短了設(shè)計(jì)周期，提高了設(shè)計(jì)效率。

國(guó)內(nèi)外專家、學(xué)者在平面葉柵優(yōu)化方面進(jìn)行了大量研究，并取得豐碩成果。如Janus等[1]采用基于步長(zhǎng)的氣動(dòng)敏感性分析新方法，對(duì)渦輪葉型局部進(jìn)行優(yōu)化。Jha[2]采用13個(gè)控制點(diǎn)的Bezier曲線進(jìn)行渦輪葉片造型設(shè)計(jì)，并采用Kreisselmeier-Steinhaus?er(K-S)算法進(jìn)行優(yōu)化。尚仁超等[3]采用參數(shù)造型法和Bezier曲線進(jìn)行葉片初步造型，并利用多目標(biāo)遺傳算法和序列二次算法組合優(yōu)化算法進(jìn)行優(yōu)化。Li等[4-5]研究了渦輪葉片的反設(shè)計(jì)優(yōu)化方法，該方法將基于控制理論的形狀優(yōu)化設(shè)計(jì)作為一種基于梯度的優(yōu)化方法。

葉柵優(yōu)化包括造型方法、性能評(píng)估方法和優(yōu)化方法三個(gè)關(guān)鍵環(huán)節(jié)，而上述成果都只偏重于其中某一環(huán)節(jié)的方法研究。本文借鑒已有研究成果，綜合考慮上述關(guān)鍵環(huán)節(jié)，葉柵造型采用更適合工程應(yīng)用的Bezier曲線參數(shù)化造型方法[6]，性能評(píng)估使用可靠的葉柵流場(chǎng)分析工具S1IC[7]，優(yōu)化方法綜合考慮了正問(wèn)題和反問(wèn)題，最終在iSIGHT平臺(tái)下對(duì)葉柵優(yōu)化過(guò)程進(jìn)行集成，建立適合工程應(yīng)用的渦輪葉柵多目標(biāo)優(yōu)化設(shè)計(jì)系統(tǒng)，并在此基礎(chǔ)上從工程應(yīng)用角度對(duì)優(yōu)化方法進(jìn)行了較為深入的討論。

2 渦輪平面葉柵數(shù)值方法

2.1 葉柵參數(shù)化造型方法

采用三條Bezier曲線控制葉柵型線，葉盆一條，葉背兩條。三段Bezier曲線除去端點(diǎn)外，需要6個(gè)葉柵型線控制參數(shù)，如圖1所示。除此之外，基本的葉柵幾何參數(shù)共12個(gè)，包括進(jìn)口結(jié)構(gòu)角、前緣直徑、尾緣直徑、有效出氣角、尾緣折轉(zhuǎn)角、前楔角、后楔角、安裝角、弦長(zhǎng)、葉片數(shù)、截面半徑、尾緣調(diào)節(jié)系數(shù)等。

圖1 葉柵參數(shù)示意圖Fig.1 The schematic diagram of cascade parameters

該葉柵參數(shù)化設(shè)計(jì)方法精確控制了葉柵喉部尺寸，保證了吸力面喉部型線的曲率連續(xù)。與傳統(tǒng)的造型曲線(如雙扭線、拋物線等)相比，這種方法可更有效地調(diào)節(jié)型線，非常適合渦輪葉柵造型設(shè)計(jì)。

2.2 平面葉柵繞流計(jì)算方法

采用S1IC程序包進(jìn)行流場(chǎng)計(jì)算。在該程序包中，利用ICEM CFD生成高質(zhì)量的三維網(wǎng)格，通過(guò)輸入y+控制附面層網(wǎng)格，分別控制葉型各個(gè)位置的網(wǎng)格數(shù)量及分布；根據(jù)給定的邊界條件和求解控制參數(shù)，自動(dòng)導(dǎo)入CFX中進(jìn)行前處理、求解和后處理等操作，輸出等熵馬赫數(shù)分布、性能參數(shù)、速度矢量圖、馬赫數(shù)等值線圖等。

S1IC程序包的計(jì)算網(wǎng)格如圖2所示，具有葉柵壁面附近網(wǎng)格正交性好、網(wǎng)格中不存在畸形點(diǎn)等優(yōu)點(diǎn)，流場(chǎng)計(jì)算易收斂，且具有較高的計(jì)算精度。

圖2 S1IC程序包計(jì)算網(wǎng)格Fig.2 The calculation mesh of S1IC

利用高壓渦輪導(dǎo)葉根截面葉柵對(duì)S1IC程序的計(jì)算精度進(jìn)行校核。圖3為計(jì)算與試驗(yàn)的表面等熵馬赫數(shù)對(duì)比，性能參數(shù)對(duì)比見(jiàn)表1，可見(jiàn)二者吻合較好，計(jì)算所得損失系數(shù)與試驗(yàn)值接近。

3 渦輪平面葉柵優(yōu)化設(shè)計(jì)集成

圖4為平面葉柵優(yōu)化設(shè)計(jì)流程圖。首先選定優(yōu)化策略，根據(jù)優(yōu)化策略給定優(yōu)化樣本。其次，根據(jù)給定樣本進(jìn)行葉片參數(shù)化造型，判斷造型結(jié)果是否滿足約束條件；滿足約束后，進(jìn)行流場(chǎng)計(jì)算，得出葉片表面等熵馬赫數(shù)分布及性能參數(shù)；對(duì)葉面等熵馬赫數(shù)分布與理想分布曲線進(jìn)行比對(duì)，評(píng)估差異，并與性能參數(shù)進(jìn)行綜合，獲得優(yōu)化目標(biāo)函數(shù)。最后，待滿足收斂條件后，終止迭代，得到最優(yōu)結(jié)果。據(jù)此流程，集成葉片造型程序，葉柵繞流計(jì)算程序及反設(shè)計(jì)模塊后的平面葉柵優(yōu)化平臺(tái)見(jiàn)圖5。

4 渦輪平面葉柵優(yōu)化方法研究

渦輪平面葉柵優(yōu)化過(guò)程，主要涉及設(shè)計(jì)變量、葉柵參數(shù)約束、優(yōu)化算法及優(yōu)化目標(biāo)的選取。在優(yōu)化變量選取上，不同優(yōu)化設(shè)計(jì)變量變化范圍對(duì)優(yōu)化結(jié)果影響不同，總存在某些變量，優(yōu)化結(jié)果對(duì)其非常敏感；還需要對(duì)葉柵參數(shù)進(jìn)行約束，以滿足結(jié)構(gòu)、強(qiáng)度設(shè)計(jì)要求，同時(shí)保證不出現(xiàn)畸形葉片；渦輪葉柵的氣動(dòng)優(yōu)化設(shè)計(jì)是典型的非線性、多峰值優(yōu)化設(shè)計(jì)問(wèn)題，不同優(yōu)化算法其優(yōu)化設(shè)計(jì)收斂過(guò)程不同，故需選取最佳優(yōu)化設(shè)計(jì)算法。能量損失系數(shù)是葉柵性能的重要衡量指標(biāo)，同時(shí)考慮到葉柵反設(shè)計(jì)通過(guò)約束葉面等熵馬赫數(shù)分布來(lái)優(yōu)化葉柵，較為適合工程應(yīng)用，所以將兩者綜合，作為優(yōu)化目標(biāo)。因此，需要研究渦輪平面葉柵優(yōu)化設(shè)計(jì)過(guò)程中的參數(shù)敏感性、優(yōu)化設(shè)計(jì)算法、多目標(biāo)優(yōu)化方法等，為渦輪平面葉柵優(yōu)化設(shè)計(jì)提供最佳的優(yōu)化方法。

以高壓渦輪導(dǎo)葉中截面(高跨聲速葉柵)為例，對(duì)上述方法進(jìn)行具體分析。葉柵主要參數(shù)見(jiàn)表2。

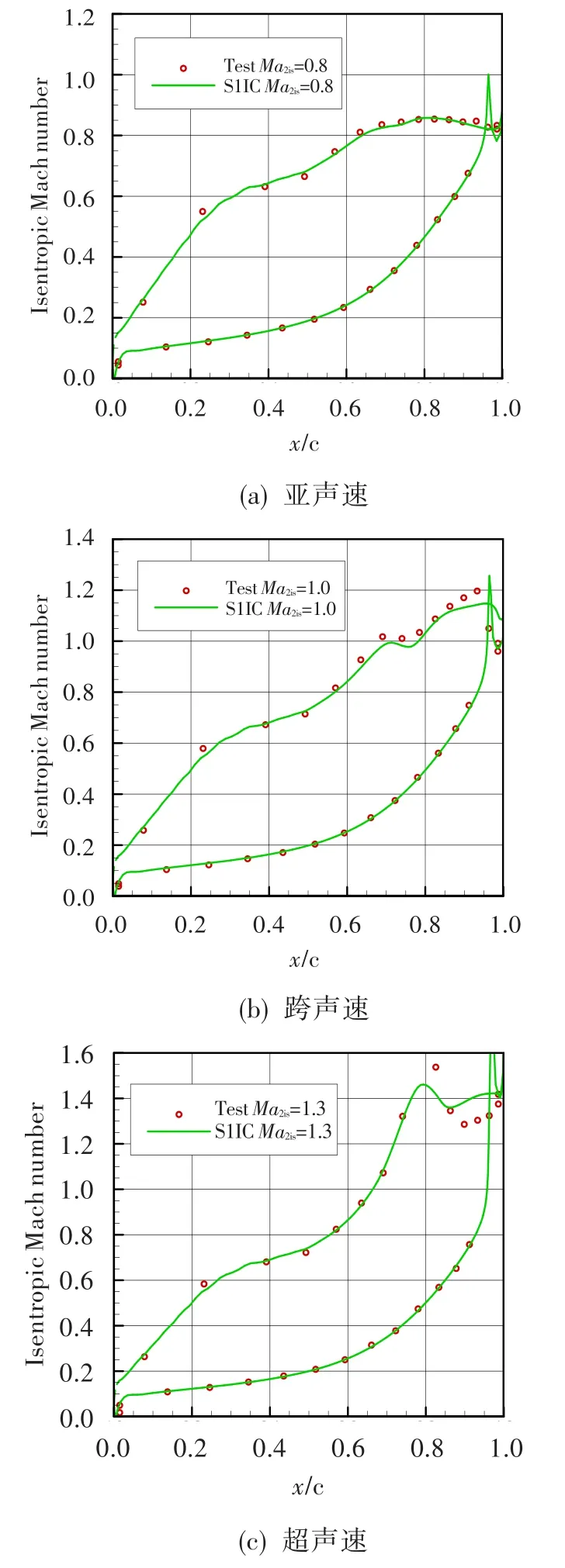
圖3 不同工況葉面表面馬赫數(shù)分布對(duì)比Fig.3 The comparison of the isentropic Mach number atdifferent operating conditions

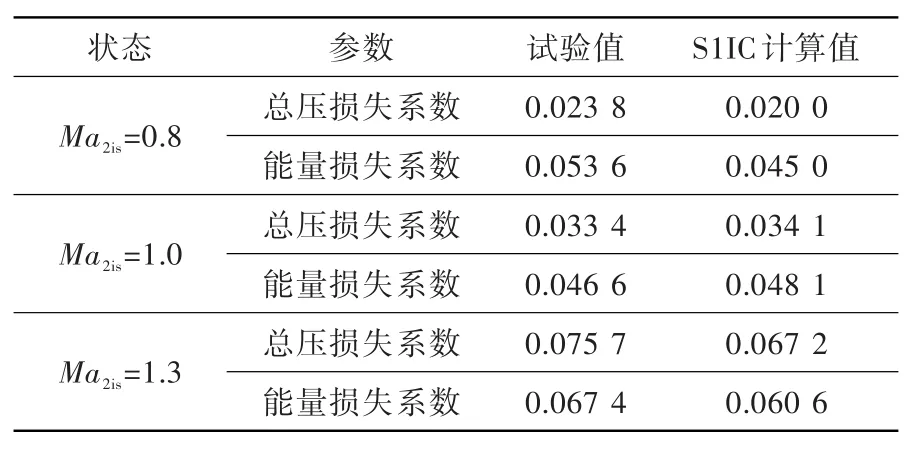
表1 性能參數(shù)對(duì)比Table 1 The comparison of performance parameters

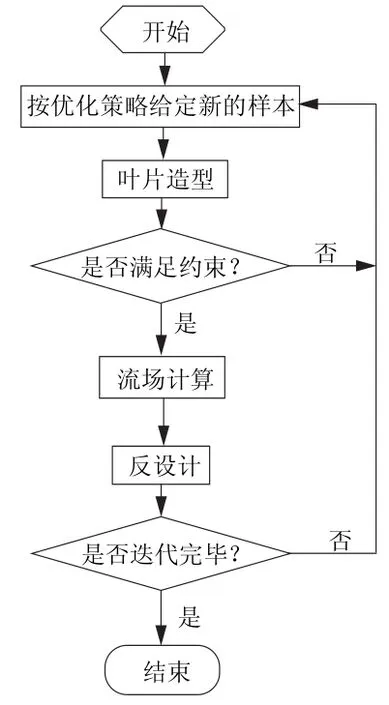
圖4 平面葉柵優(yōu)化設(shè)計(jì)流程Fig.4 The flow chart of cascade optimization design

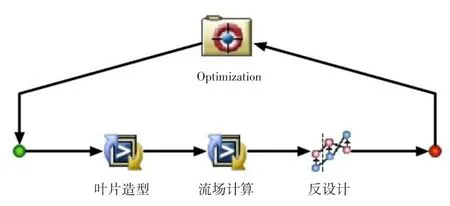
圖5 平面葉柵優(yōu)化設(shè)計(jì)平臺(tái)Fig.5 The platform of cascade optimization design

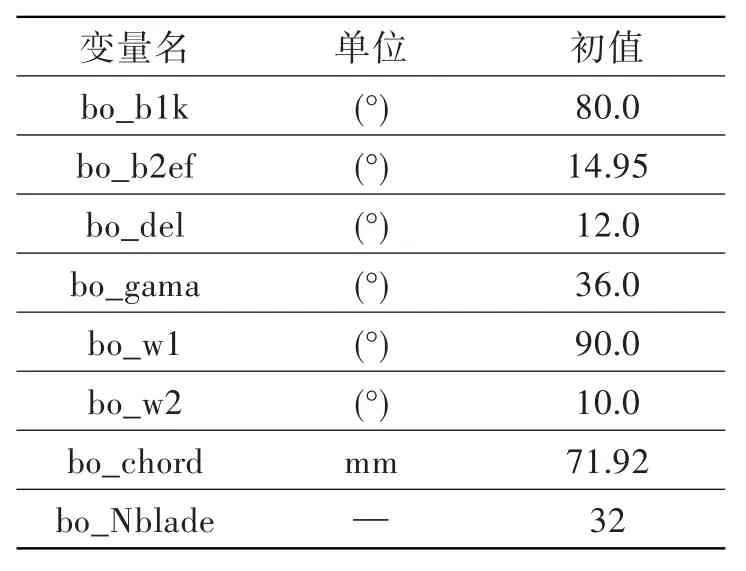
表2 葉柵主要參數(shù)Table 2 The dominating parameters of cascade

4.1 參數(shù)敏感性分析

平面葉柵優(yōu)化設(shè)計(jì)參數(shù)多(18個(gè))，故在優(yōu)化設(shè)計(jì)方案時(shí)需選適當(dāng)?shù)脑O(shè)計(jì)變量。如果對(duì)葉片幾何與流動(dòng)性能的關(guān)系分析不徹底，將導(dǎo)致優(yōu)化變量多、工作量大，難以實(shí)現(xiàn)有效的優(yōu)化設(shè)計(jì)。因此，需要開展參數(shù)敏感性分析，剔除敏感性相對(duì)較差的變量。首先，葉柵優(yōu)化會(huì)選擇適當(dāng)?shù)慕孛婧腿~片數(shù)，而尾緣調(diào)節(jié)系數(shù)用于保證葉背兩條型線連接時(shí)曲率連續(xù)，因此不做優(yōu)化考慮。應(yīng)用優(yōu)化平臺(tái)先對(duì)剩余葉柵參數(shù)進(jìn)行試驗(yàn)設(shè)計(jì)，獲得各設(shè)計(jì)參數(shù)對(duì)葉柵性能的貢獻(xiàn)率。

圖6示出了葉柵各設(shè)計(jì)參數(shù)的貢獻(xiàn)率。可見(jiàn)，尾緣直徑和有效出氣角對(duì)損失的貢獻(xiàn)率最高，6個(gè)型線控制參數(shù)對(duì)損失的影響也較大，接下來(lái)是尾緣折轉(zhuǎn)角、尾緣楔角和安裝角。尾緣直徑直接影響尾緣損失，有效出氣角則關(guān)乎葉柵喉部尺寸，所以損失對(duì)它們的敏感性很高；尾緣折轉(zhuǎn)角控制葉柵通道喉部位置之后的吸力面葉型曲率，從而影響葉片尾緣位置通道收斂性，特別是對(duì)高出口馬赫數(shù)葉柵的尾緣激波強(qiáng)度有很大影響；尾緣楔角影響著速度場(chǎng)的不均勻度及葉柵出口總壓差，對(duì)性能影響較明顯；安裝角受進(jìn)出口氣流角和稠度影響，存在最佳值，對(duì)葉片負(fù)荷有重要影響。考慮到尾緣直徑受加工工藝及冷卻要求的限制，而有效出氣角用于匹配調(diào)節(jié)，所以不把這兩個(gè)參數(shù)作為優(yōu)化變量。因此，本文以控制點(diǎn)參數(shù)(bo_sl1、bo_sl2、bo_st1、bo_st2、bo_p1、bo_p2)，尾緣折轉(zhuǎn)角(bo_del)，安裝角(bo_gama)，后楔角(bo_w2)等9個(gè)變量作為設(shè)計(jì)變量。

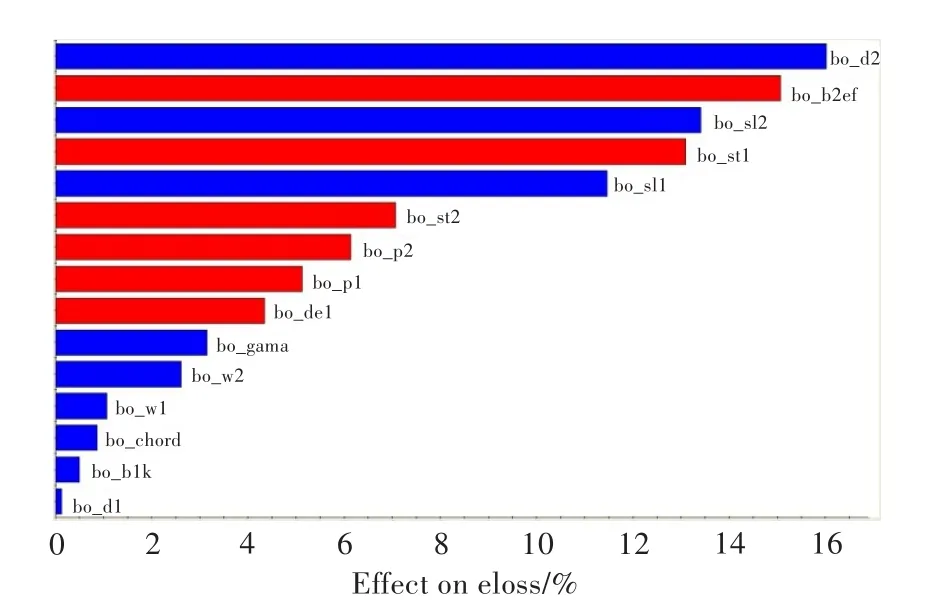
圖6 葉柵各設(shè)計(jì)參數(shù)貢獻(xiàn)率Fig.6 The contribution of cascade parameters

4.2 優(yōu)化算法分析

渦輪平面葉柵氣動(dòng)優(yōu)化設(shè)計(jì)是典型的非線性、多峰值優(yōu)化設(shè)計(jì)問(wèn)題，因此，優(yōu)化算法必須具有優(yōu)秀的魯棒性和搜索效率。iSIGHT平臺(tái)的優(yōu)化算法，包括數(shù)值型優(yōu)化算法、探索型優(yōu)化算法、專家系統(tǒng)技術(shù)三類，但是數(shù)值型優(yōu)化算法一般都假定參數(shù)空間是單峰的、凸的和連續(xù)的，因此僅考慮其他兩種典型算法。

選取多島遺傳算法(MIGA)、自適應(yīng)模擬退火算法(ASA)及優(yōu)化專家(Pointer)算法進(jìn)行測(cè)試對(duì)比，為渦輪平面葉柵優(yōu)化算法的選取提供依據(jù)，圖7為各優(yōu)化算法的收斂史。可見(jiàn)：只要時(shí)間足夠，三種算法都能找到全局最優(yōu)解。由于MIGA算法在每次探索時(shí)檢查一組設(shè)計(jì)點(diǎn)(由子群、島數(shù)和代數(shù)決定)，故需要很大的計(jì)算量才能找到最優(yōu)解；Pointer算法對(duì)初始點(diǎn)的依賴較多，容易陷入局部最優(yōu)解；ASA算法在初始點(diǎn)附近就有小幅波動(dòng)，即目標(biāo)函數(shù)值上升的點(diǎn)也可能被接受，從而避免陷入局部最優(yōu)點(diǎn)，且收斂速度較其他兩種算法快。綜合考慮三種優(yōu)化算法的優(yōu)劣，優(yōu)化設(shè)計(jì)采用ASA算法。

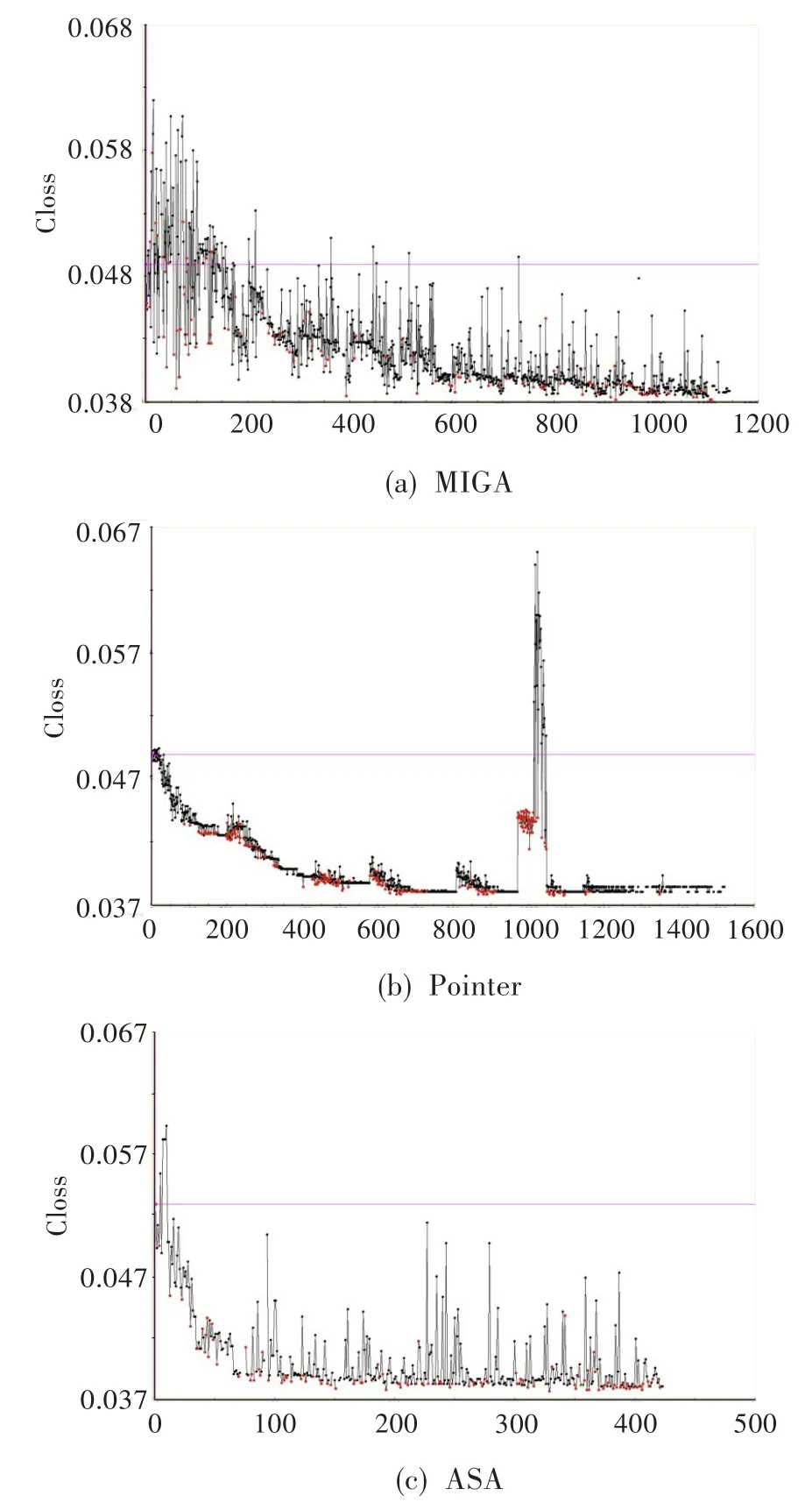
圖7 各優(yōu)化算法的收斂史Fig.7 The convergence history of the various methods

4.3 反設(shè)計(jì)方法

葉柵反設(shè)計(jì)，即通過(guò)壓力或馬赫數(shù)分布，反推葉柵參數(shù)。通過(guò)對(duì)原始葉柵的流動(dòng)分析，可得到一個(gè)可能的理想馬赫數(shù)分布曲線，這樣就可對(duì)每次迭代運(yùn)算后的葉柵馬赫數(shù)分布加以約束，使其接近理想曲線分布。具體方法為，只考慮吸力面馬赫數(shù)分布，如圖8所示，給定理想馬赫數(shù)分布曲線(Target)與計(jì)算所得馬赫數(shù)分布曲線(Calculation)，同一相對(duì)弦長(zhǎng)位置上馬赫數(shù)值差的平方和作為一個(gè)優(yōu)化目標(biāo)，那么當(dāng)該值趨于最小時(shí)，葉柵馬赫數(shù)分布最接近目標(biāo)曲線分布。

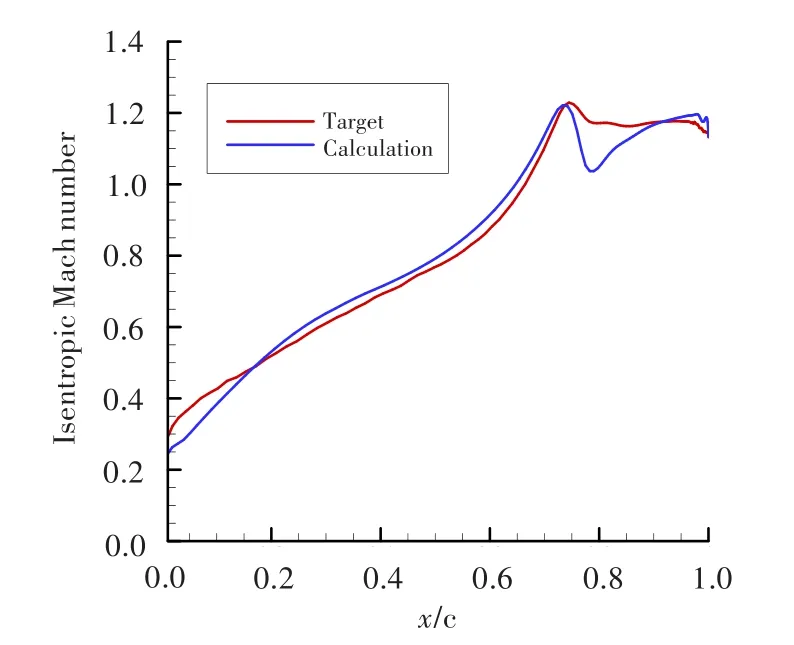
圖8 馬赫數(shù)分布曲線優(yōu)化示意圖Fig.8 The schematic diagram of the isentropic Mach number optimization

4.4 多目標(biāo)優(yōu)化方法

將能量損失和馬赫數(shù)分布曲線約束作為優(yōu)化目標(biāo)，并采取權(quán)重法進(jìn)行處理，即把多個(gè)目標(biāo)轉(zhuǎn)化成單一目標(biāo)進(jìn)行優(yōu)化。

4.5 優(yōu)化結(jié)果分析

采用上述方法對(duì)該葉柵進(jìn)行優(yōu)化設(shè)計(jì)，設(shè)計(jì)變量設(shè)置詳見(jiàn)表3，給定進(jìn)口氣流角(10°)和壓比(0.48)，對(duì)葉型面積進(jìn)行約束(600 mm2＜area＜800 mm2)，給定優(yōu)化目標(biāo)最小，權(quán)重系數(shù)都設(shè)置為0.5。

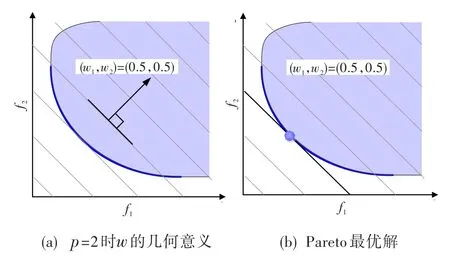
圖9 兩個(gè)優(yōu)化目標(biāo)時(shí)權(quán)重的幾何意義和Pareto最優(yōu)解Fig.9 The geometric significance ofwand the Pareto optimal solution

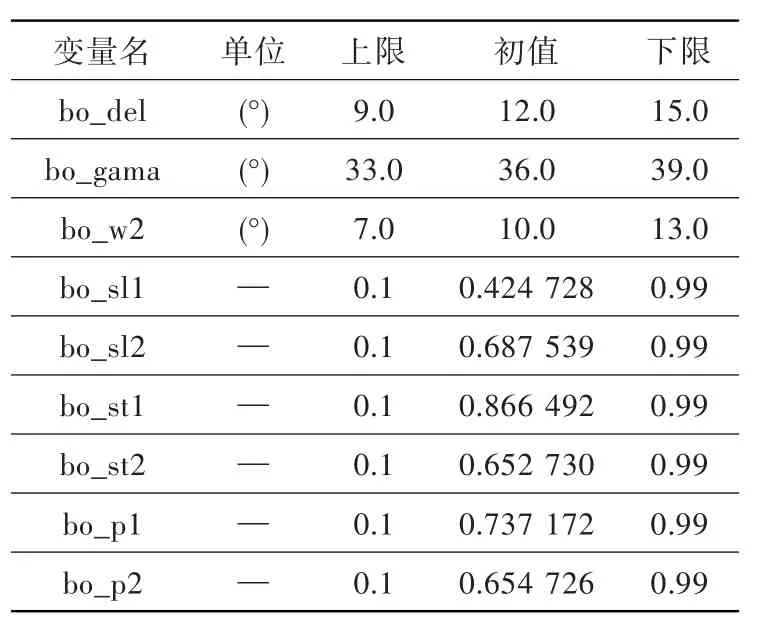
表3 參數(shù)設(shè)置Table 3 The parameters setting

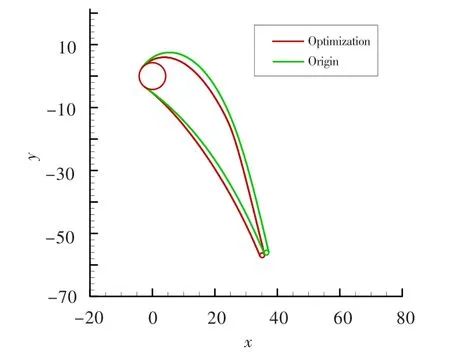
圖10 優(yōu)化前后葉型對(duì)比Fig.10 The comparison of cascade before and after optimization

優(yōu)化前后葉型對(duì)比見(jiàn)圖10，葉柵表面等熵馬赫數(shù)對(duì)比見(jiàn)圖11。從圖11中可看出，優(yōu)化后的葉柵很大程度上降低了尾緣處的逆壓梯度，吸力面葉柵馬赫數(shù)從峰值很平穩(wěn)地過(guò)渡到出口狀態(tài)，大大改善了葉柵性能，且使吸力面壓力分布的變化更為平緩。優(yōu)化前后性能參數(shù)對(duì)比見(jiàn)表4，可見(jiàn)優(yōu)化前后出口馬赫數(shù)及出口氣流角并未有太大變化，但葉柵性能大大改善，能量損失與壓力損失相對(duì)于初始值有16%左右的降幅。

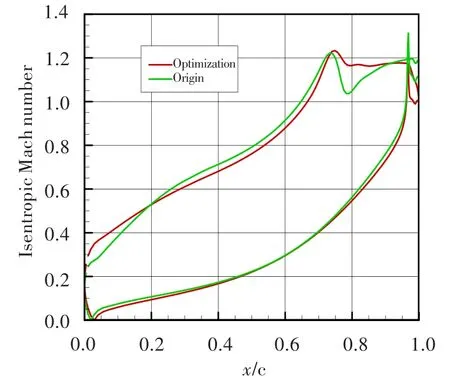
圖11 優(yōu)化前后表面等熵馬赫數(shù)對(duì)比Fig.11 The comparison of the isentropic Mach number before and after optimization

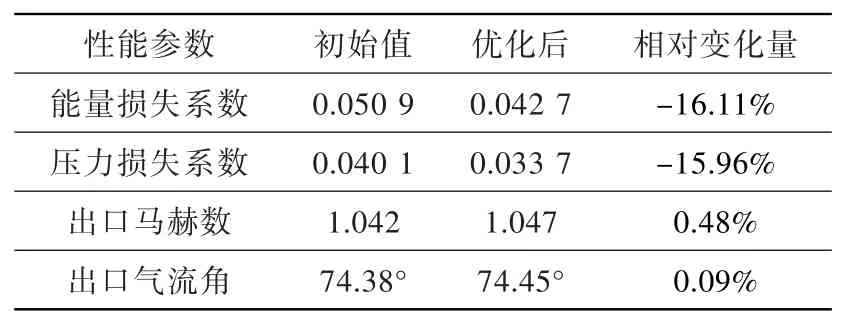
表4 優(yōu)化前后性能參數(shù)對(duì)比Table 4 The comparison of performance parameters before and after optimization

5 結(jié)論

本文闡述的渦輪平面葉柵優(yōu)化方法基于iSIGHT平臺(tái)，采用一定的優(yōu)化策略，將成熟的渦輪葉柵造型軟件和葉柵性能評(píng)估軟件集成，形成渦輪平面葉柵優(yōu)化系統(tǒng)。優(yōu)化之初，首先開展參數(shù)敏感性分析，明確對(duì)葉柵優(yōu)化較為重要的參數(shù)，剔除貢獻(xiàn)率小的參數(shù)，以提高優(yōu)化效率。對(duì)優(yōu)化算法的考核表明，自適應(yīng)模擬退火方法較為適用于渦輪葉柵優(yōu)化。優(yōu)化目標(biāo)將葉柵設(shè)計(jì)的正、反問(wèn)題有機(jī)結(jié)合，使得渦輪葉柵的優(yōu)化工作更加靈活。實(shí)踐證明，該方法可快速有效地對(duì)渦輪葉柵流場(chǎng)和性能進(jìn)行優(yōu)化，較為適合工程應(yīng)用。

[1]Janus J M，Newman IIIJ C.Aerodynamic and thermal de?sign optimization for turbine airfoils[R].AIAA 2000-0840，2000.

[2]Jha R.Development of multidisciplinary optimization pro?cedure for smart composite wings and turbomachinery blades[D].Arizona：Arizona State University，1999.

[3]尚仁超，喬渭陽(yáng).基于參數(shù)法和貝塞爾曲線的渦輪葉片造型及其優(yōu)化[J].機(jī)械設(shè)計(jì)與制造，2007，(8)：16—18.

[4]Li Ying-chen，Yang Dian-liang，F(xiàn)eng Zhen-ping.Inverse problem in aerodynamic shape design of turbomachinery blades[R].ASME GT2006-91135，2006.

[5]Li Ying-chen，F(xiàn)eng Zhen-ping.Aerodynamic design of turbine blades by using adjoint-based method and N-S equation[R].ASME GT2007-27734，2007.

[6]李劍白，卿雄杰，周山，等.渦輪葉片氣動(dòng)設(shè)計(jì)軟件BladeDesign[J].燃?xì)鉁u輪試驗(yàn)與研究，2011，24(3)：12—13.

[7]卿雄杰.渦輪全三維計(jì)算軟件深度開發(fā)[C]//.中國(guó)航空學(xué)會(huì)第十七屆學(xué)術(shù)交流會(huì)議論文集.2013.

Turbine cascade multi-objective optimization design based on the parameter susceptibilities

LAI Wei，LI Jian-bai，ZHANG Jian
(China Gas Turbine Establishment，Chengdu 610500，China)

Based on the existing research results,a new turbine cascade optimization method was devel?oped,which was synthesized with the three key points:the cascade geometry design,performance assess?ment and optimization method.The integration of the optimization process was achieved in the iSIGHT plat?form.A multi-objective optimization design system of turbine cascade was established,which was suitable for the engineering application.Taking the middle section of a high pressure turbine cascade as an example, the further analysis was made in three ways:the parameter susceptibilities the inverse design of cascade and multi-objective optimization.The results indicate that the new method is able to optimize the flow field and performance of cascade quickly and efficiently.

turbine cascade；parameter susceptibilities；inverse design；multi-objective optimization；optimization method；engineering application

V231.3

A

1672-2620(2015)01-0054-06

2014-06-23；

2015-02-05

賴巍(1981-)，男，滿族，河北廊坊人，工程師，碩士，主要從事渦輪氣動(dòng)設(shè)計(jì)和試驗(yàn)研究。