基于Berreman 4×4矩陣對膽甾相液晶Bragg反射帶寬的模擬研究

趙 靜?,李慶麗,許利軍

(張家口學院,河北張家口075000)

基于Berreman 4×4矩陣對膽甾相液晶Bragg反射帶寬的模擬研究

趙 靜?,李慶麗,許利軍

(張家口學院,河北張家口075000)

利用Berreman 4×4矩陣和Matlab編程模擬了膽甾相液晶的反射光譜,分析了螺旋數(液晶厚度)、基板的折射率、雙折射、折射率色散、固定螺距、梯度螺距和入射角等因素對反射光譜帶寬的影響。結果表明,要得到理想的Bragg反射帶寬,液晶層的厚度即螺旋數N需達到N≥10;基板折射率會影響最大反射率,基板折射率ng與尋常光折射率no相比, ng＜no時,最大反射率比較低,ng越小越影響明顯,當ng≥no時,具有很好的反射率;折射率的色散和大的入射角會使帶寬變窄,而大的雙折射Δn和螺距P可以得到較寬的反射帶寬,但拓寬效果有限。通過梯度螺距的函數表達式,理論模擬了具有螺距梯度的膽甾相液晶的反射帶寬,其對于膽甾相液晶寬波反射的實驗研究具有一定的意義。

膽甾相液晶;Berreman 4×4矩陣;Bragg反射;帶寬;螺距梯度

Key words:cholesteric liquid crystal;Berreman 4×4 matrix;Bragg reflection;bandwidth;pitch gradient

1 引 言

膽甾相液晶大致可分為含膽固醇基環的膽固醇衍生物和把光學活性添加劑加入向列相液晶使液晶分子排列轉變形成的膽甾相液晶。在空間上膽甾相液晶的指向矢n并不一致,而是沿著螺旋軸盤旋而上,因此液晶分子的指向矢在螺旋軸上具有周期性。將指向矢旋轉360°的間距稱為一個螺距,一般用P表示。由于n和-n的不可區分性,所以膽甾相液晶的空間周期L是其螺距P的一半。螺旋狀的分子排列,使膽甾相液晶具有獨特的光學性質,其中最重要的特性之一就是Bragg反射。近些年來,膽甾相液晶的Bragg反射是人們研究的熱點問題。尤其是將膽甾相液晶應用反射式顯示,反射式偏振片,濾光片,光學增亮膜,節能玻璃及涂料等方面[1-4],但其也存在一個很大的缺點就是Bragg反射光譜帶寬的寬度不夠,一般只有幾十納米,遠遠不能覆蓋整個可見光區域,這就給膽甾相液晶的實際應用帶來一些不利影響,例如在顯示方面,這樣就容易形成單色,而顏色與視角的相依性又很高。從而有許多研究以試圖增加膽甾相液晶反射光譜的帶寬,Broer等人利用紫外光可聚合的膽甾相液晶單體與向列相液晶單體作為偏光材料,通過紫外光照射產生的濃度擴散效應使螺距產生梯度變化來拓展反射帶寬[5],Kralik等人和美國中央弗羅里達大學的Yu hua Huang等人通過多層單一螺距疊加的方法使反射光覆蓋可見光區域[6-7],黃子強等人通過在液晶中引入納米粒網絡來展寬反射光譜[8]。在這些研究中,目前最常用的方法是通過某種方式(紫外線誘導、溫度梯度等)使膽甾相液晶產生螺距梯度,從而反射帶寬隨著螺距的變化而加寬。

本文利用Berreman 4×4矩陣和Matlab編程模擬了膽甾相液晶的反射光譜,分析了影響反射帶寬的因素,如螺旋數、基板的折射率、折射率色散、梯度螺距和入射角等,對拓展Bragg反射帶寬進行了深入闡述,計算模擬結果對于膽甾相液晶寬波反射的實驗研究具有一定的意義。

2 理論分析

2.1 反射率計算

光在膽甾相液晶中傳播如圖1所示,假設入射光在x-z平面入射。根據麥克斯韋方程可以得到:

圖1 光在膽甾相液晶中傳播的坐標示意圖Fig.1 Coordinate diagram of light propagation in cholesteric liquid crystal

Δ矩陣被稱為Berreman4×4矩陣[9],其依賴于膽甾相液晶的介電常數并且為z的函數,在z附近有一個微小的變動h,若h足夠小,可將其看作一個常數時,方程(1)的解可寫成:

假設整個液晶盒中的液晶分為M層,根據式(2)可以得到:

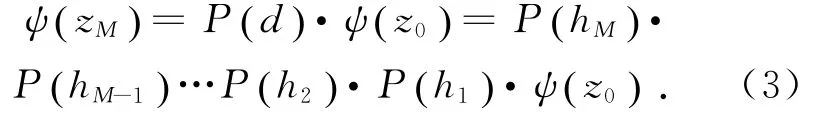
在z＝0和z＝d處,由電磁場邊界條件,其電磁場在邊界的切線分量是連續的,可得:

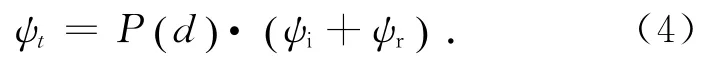
假設膽甾相液晶夾在兩個折射率為ng的基板之間,則入射光、反射光和透射光的Berreman矢量可分別表示為:

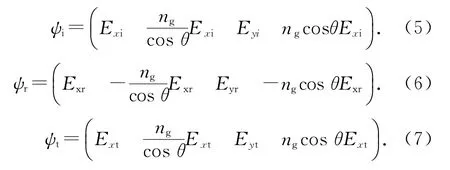
只要給出了入射光的Berreman矢量ψi,就可以通過解(4)式求得ψr和ψt中兩個未知的變量Ex、Ey。

反射率的計算公式為[9]:

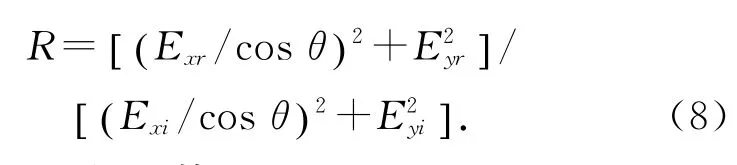
2.2 Bragg反射計算

當光正入射時,Bragg中心反射波長和反射光譜帶寬分別為:

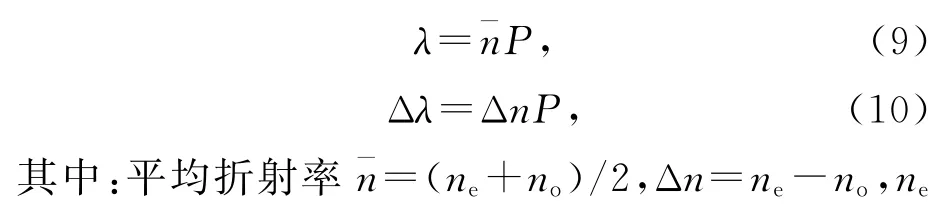
和no分別為液晶的非尋常光和尋常光折射率。

當光斜入射時,Bragg中心反射波長和反射帶寬為:

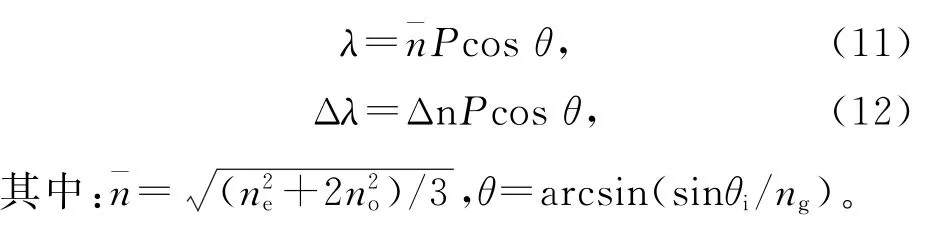
當螺旋軸與基板法線有夾角φ時,Bragg中心反射波長和反射帶寬為:

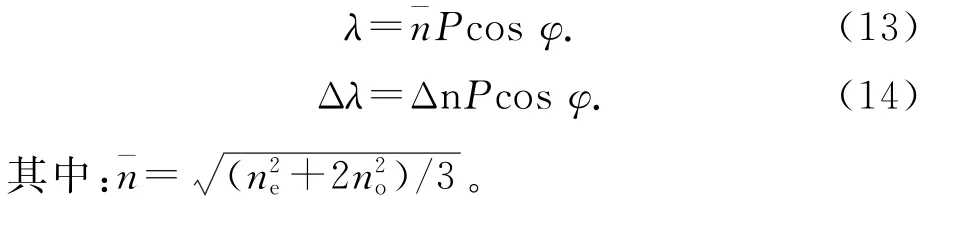
3 結果與討論

在模擬中,入射光為圓偏振光且螺旋性與膽甾相液晶相同,只考慮光從基板進入膽甾相液晶,基板的折射率為ng。假設兩邊基板材質相同,則在圖1中θt＝θr＝θi＝θ0。膽甾相液晶的折射率和螺距參數設置隨模擬情況的不同而不同。下面具體分析螺旋數、基板折射率等參數對膽甾相液晶Bragg反射帶寬的影響。

3.1 螺旋數N的影響

由于Bragg反射靠的是光在周期性結構內多重反射所形成的加強干涉,因此膽甾相液晶中周期性結構的數量就成了很重要的參數。通過定義一個螺旋數N來表示此參數。假設膽甾相液晶的螺距為定值P,因此液晶盒的厚度成了離散的分布。螺旋數N與液晶盒厚度d由下式定義:

圖2為不同螺旋數的模擬結果(ne＝1.75, no＝1.52,ng＝1.52,P＝0.37μm,θi＝0°,N＝1、3、5、8、10、12、14)。從圖中可以看出,當N＝1 時,Bragg反射的峰值并不明顯且反射率非常低; N＝3時,出現明顯反射峰值,但其反射帶寬非常窄并且中心反射波長的反射率較低;N＝8時,具有很好的反射峰值和帶寬,具有很高的反射率,但是其帶寬邊緣不太明顯;當N≥10時,反射帶寬和帶寬邊緣非常明顯,且接近于全反射。因此,要得到具有明顯帶寬的反射光譜,膽甾相液晶的厚度需要達到一定的螺旋數。將ne、no、P的值帶入Bragg反射公式(9)和(10),中心反射波長和帶寬分別為604.95 nm和85.1 nm,在具有明顯反射峰值和帶寬的情況下,其與圖2模擬的結果有很好的吻合度。

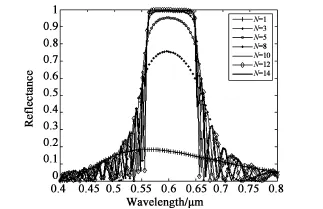
圖2 不同螺旋數N的Bragg反射Fig.2 Bragg reflections with different pitch number N

3.2 基板折射率的影響

從圖3可以看出當ng＜n0時,最大反射率比較低,ng越小越影響明顯,但其不影響反射光譜的帶寬;當ng≥n0時,具有很好的反射率和反射帶寬,ng對反射率和反射光譜基本沒有影響。膽甾相液晶兩側基板的折射率雖然對反射光譜的帶寬沒有影響,但其會影響反射光譜的最大反射率。

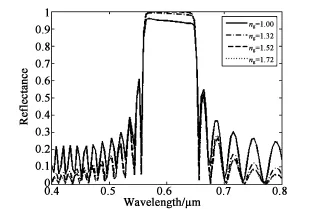
圖3 不同基板折射率的Bragg反射Fig.3 Bragg reflections with different substrate refractive index

3.3 折射率色散的影響

在實際的液晶材料中,折射率一般會存在色散,它與波長的關系如下[10]:

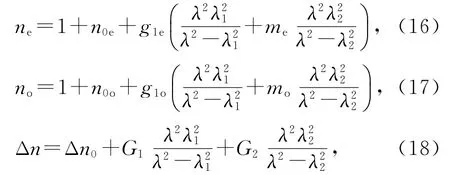
其中:Δn0＝n0e－n0o,G1＝g1e－g1o,G2＝g2e－g2o, me＝0.5,mo＝1,n0e＝0.455,n0o＝0.405,g1e＝1.830,g1o＝1.313,λ1＝200 nm,λ2＝282 nm。則液晶的折射率與波長的關系如圖4所示。

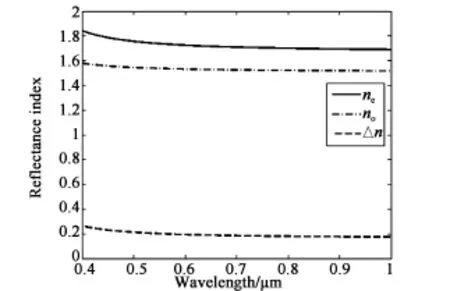
圖4 折射率的色散Fig.4 Dispersion of refractive index

從圖4中可以看出,液晶的折射率隨波長的增加而減小,這將會導致在短波區域液晶的折射率相對較高,反射會向長波方向移動,在長波區域液晶的折射率相對較低,反射會向短波方向移動,從而造成反射光譜帶寬變窄。同時由于液晶的雙折射隨著波長的增加而減小,在長波區域反射帶寬會變窄,所以在長波區域的Bragg反射一定要考慮膽甾相液晶材料的色散對反射帶寬的影響。

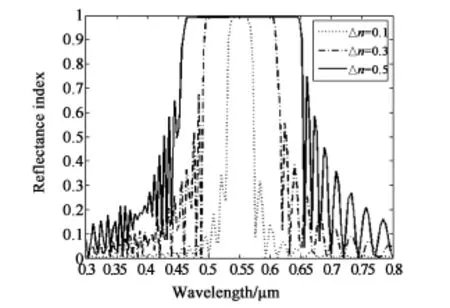
圖5 不同雙折射Δn的Bragg反射Fig.5 Bragg reflections with different birefringenceΔn

3.4 雙折射的影響

從式(10)可以看出,在螺距固定的情況下,膽甾相液晶反射光譜的帶寬與雙折射Δn成正比關系,隨著Δn的增加,反射帶寬也隨之變寬。圖5給出了正入射情況下,反射帶寬隨Δn的變化。在模擬過程中保持中心反射波長不變,P＝0.34 μm,d＝16P,Δn分別取0.1,0.3,0.5。將P和Δn的值帶入(10)式,可得帶寬分別為34 nm、102 nm、170 nm,對比圖5和式(10)的結果,兩者吻合得很好。從圖5中可以看出,大的Δn可以拓展反射帶寬。但由于受到液晶分子自身的限制,Δn是不能任意增加的,其值一般不超過0.3。同時,即使具有很高Δn(0.5)的液晶,其反射帶寬僅有170 nm,遠不足以覆蓋整個可見光區域。因此,盡管具有高雙折射率的液晶可以被用來拓展帶寬,但簡單的增加Δn并不能得到滿足液晶顯示設備所需的帶寬。

3.5 螺距的影響

實際上，在1970年代末創作出《蕨類植物》和《放射性的貓》后，斯各格蘭德已經走上了專屬于她的獨特藝術道路，滿足了她對繪畫、電影和攝影多種藝術形式的熱愛。現在的她已成功集編劇、舞臺設計師、畫家、雕塑家、導演以及攝影師等身份與一體。

改變膽甾相液晶的Bragg反射帶寬,除了改變液晶的折射率外,還可以通過改變其螺距來實現。通過式(10)可以看出,Δn固定的情況下,大的螺距P也可以拓展反射帶寬。但在實際應用中,多數是通過具有梯度變化的螺距來拓展反射帶寬的。下面分兩種情況來分析。

3.5.1 Δn固定,不同的固定螺距

從圖6可以看出,在正入射情況下,Δn(ne＝1.75,no＝1.52)固定,螺距P分別為0.28μm、0.34μm、0.40μm。隨著螺距的增大,反射帶寬也增大,反射中心波長也向長波方向移動,產生紅移并且其中心反射波長和帶寬與(9)、(10)的計算結果相符。但從增加帶寬以使其覆蓋可見光區域并應用于顯示設備的方面考慮,并且根據Bragg反射和螺距數的關系,大螺距要想產生很好的Bragg反射也需要較厚的液晶盒,增加生產成本,故此種方法并不可取。

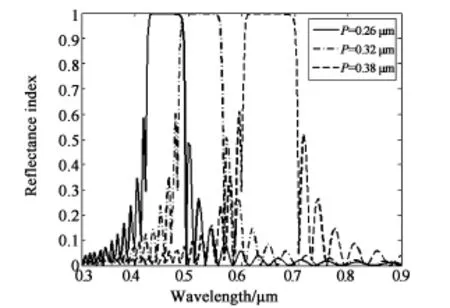
圖6 不同螺距的Bragg反射Fig.6 Bragg reflections with different pitch

3.5.2 螺距梯度

1995年Broer等學者引入了螺距變化概念,通過某種方法使膽甾相液晶的螺距產生梯度變化,而反射帶寬由于螺距的變化而加寬,其反射帶寬可以用式(19)表示: Δλ＝n//Pmax－n⊥Pmin, (19)其中:Pmax和Pmin分別為最大螺距和最小螺距,反射帶寬由與位置相關的螺距與雙折射而定。螺距梯度結構可以用數學式來表示。

假設螺距梯度變化為線性函數,可以有兩種描述方式[11]:

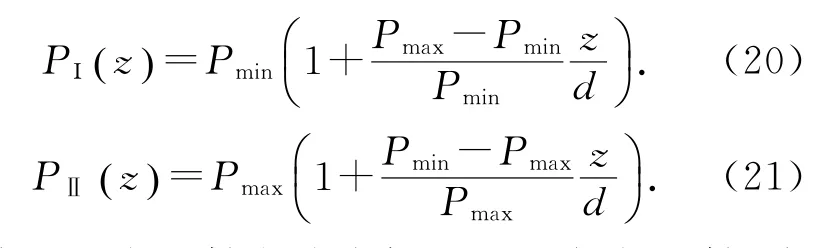
式(20)為入射光從小螺距Pmin方向入射,式(21)表示入射光從大螺距Pmax方向入射。圖7給出了螺距變化按式(20)表示的膽甾相液晶的反射光譜,其中Pmin＝0.24μm,Pmax＝0.40,ne＝1.82,no＝1.52,ng＝1.52,d＝12Pmin。將以上各數值帶入(19)式得反射帶寬為363.2 nm,其結果與圖7對比相吻合。

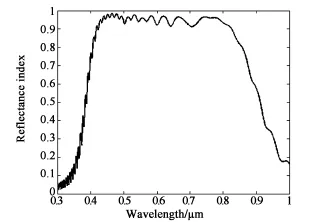
圖7 PⅠ的Bragg反射對比Fig.7 Bragg reflections with PⅠ

從圖7可以看出,具有線性變化螺距的膽甾相液晶的反射帶寬幾乎可以覆蓋整個可見光區域。如果適當向長波方向拓寬,可以補償由于入射角不同而引起的藍移。與等螺距膽甾相液晶在反射光譜上的另一個差別就是在反射帶邊緣的輪廓沒有劇烈振蕩,主要是因為螺距梯度的周期變化不如等螺距的周期變化那么嚴格,也可說螺距梯度結構實際上根本沒有周期可言,只是螺距的變化有規則而已,因此在反射上因介電常數周期交錯所產生的干涉現象并不會很劇烈。

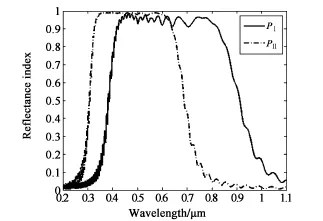
圖8 PⅠ和PⅡ的Bragg反射對比Fig.8 Comparsion of Bragg reflections between PⅠand PⅡ

具有PⅠ和PⅡ兩種線性螺距梯度的膽甾相液晶的Bragg反射會存在很大差異。取與圖7相同的參數進行模擬,結果如圖8所示。從圖中發現,PⅡ的反射光譜要比PⅠ的平滑,向短波方向移動且Bragg反射帶寬變窄。

3.6 入射角的影響

隨著入射角的增大,膽甾相液晶的Bragg反射中心波長會向短波方向移動,產生藍移現象,如圖9所示(ne＝1.75,no＝1.52,ng＝1.52,P＝0.37μm,d＝12P,θi＝0°、10°、20°)。從圖9中可以看出反射光譜的帶寬也稍微變窄,中心波長和反射帶寬隨入射角的變化滿足Bragg反射公式(11)和(12)。

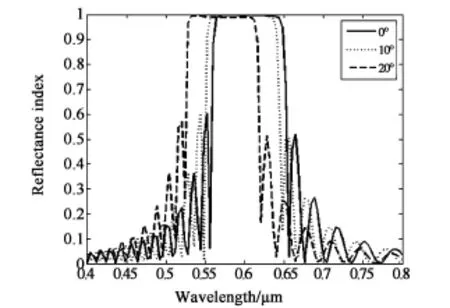
圖9 不同入射角的Bragg反射Fig.9 Bragg reflections with different incident angle

假設膽甾相液晶的螺旋軸與基板的法線有夾角φ。在正入射情況下,其中心反射波長與反射帶寬可以用(13)和(14)式來表示。所以隨著螺旋軸與基板夾角的增大,中心反射波長向短波方向移動,反射帶寬也變窄。因此在實際應用中,如果膽甾相液晶的螺旋軸不垂直于基板,則會產生藍移現象,并且使反射帶變窄。

4 結 論

利用4×4矩陣法并通過Matlab對膽甾相液晶反射光譜進行模擬,分析了影響反射光譜帶寬的因素,如螺旋數N、基板折射率、雙折射、固定螺距和梯度螺距等。從模擬結果發現:膽甾相液晶Bragg反射的光譜帶寬和峰值與螺旋數有很大的關系,要得到完美的反射光譜,液晶層要有一定的螺旋數(厚度),在本文模擬中螺旋數N滿足N≥10,反射光譜才有明顯的反射帶寬及帶寬邊緣,所以在實際應用中一定要注意液晶盒的厚度和反射帶寬的關系;液晶兩側基板的折射率雖然不會影響反射光譜的帶寬,但會對最大反射率產生一定的影響,當基板折射率和液晶折射率滿足ng≥no時,這種影響將會被消除,所以實際應用時一定要考慮基板的折射率和液晶的折射率的匹配關系;實際中液晶的折射率存在色散,即ne、no、Δn都是波長的函數,這將在一定程度上導致反射帶寬變窄;隨著入射角或螺旋軸和基板法線之間夾角的增大,反射帶寬會變窄并向短波方向移動,產生藍移現象;大的雙折射Δn和螺距P可以得到較寬的反射帶寬,但其拓寬效果有限,而具有梯度變化的螺距對反射帶寬的拓寬效應非常明顯,可以使反射光譜很容易的覆蓋整個可見光區域,其理論計算模擬的拓展效果與已有的實驗結果相符,這對具有寬波反射的膽甾相液晶的實驗研究具有一定的意義。

[1] 張天翼,許軍,董佳垚.膽甾型液晶顯示技術和產業發展[J].液晶與顯示,2011,26(6):741-745.Zhang T Y,XU J,Dong J Y.Overview of technology and industry for cholesteric liquid crystal display[J].Chinese Journal of Liquid Crystals and Displays,2011,26(6):741-745.(in Chinese)

[2] 李樂,李建峰,范炳生,等.反射式膽甾相液晶偏振片及其應用[J].現代顯示,1998,4(18):29-35.Li L,Li J F,Fan B S,et al.Reflective cholesteric liquid crystal polarizers and their applictions[J].Advanced Display,1998,4(18):29-35.(in Chinese)

[3] 張大勇,李劍鋒,劉倉理,等.手性液晶濾光片研究[J].應用激光,2005,25(5):316-317.Zhang D Y,Li J F Liu C L,et al.Study of cholesteric liquid crystals filter[J].Applied Laser,2005,25(5):316-317.(in Chinese)

[4] Moriya T N,Uchida,Matsushima K.用膽甾液晶制備的新型寬視角透過式彩色濾光片[J].現代顯示,2004,1 (41):42-44.Moriya T N,Uchida,Matsushima K.Novel transmissive color filter using cholesteric liquid crystal with wide viewing angle[J].Advanced DI,2004,1(41):42-44.(in Chinese)

[5] Broer D J,Lub J,Mol G N.Wide-band reflective polarizers from cholesteric polymer networks with a pitch gradient[J].Nature,1995,378(6556):467-469

[6] Kralik J C,Fan B,Vithana H,et al.Backlight output enhancement using cholesteric liquid crystal films[J].Mol.Cryst.Liq.Cryst.,1997,301:798-794

[7] Huang Y,Zhou Y,Wu S T.Broadband circular polarizer using stacked chiral polymer films[J].Opt.Express, 2007,15(10):6414-6419.

[8] 黃子強,楊文君,王繼敏.納米網絡對手性液晶反射光譜的展寬效應[J].液晶與顯示,2006,21(1):1-5.Huang Z Q,Yang W J,Wang J M.Bragg reflective spectrum broadened by nano-particle-network in chiral liquid crystals[J].Chinese Journal of Liquid Crystals and Displays,2006,21(1):1-5.(in Chinese)

[9] Berreman D W.Optics in stratified and anisotropic media:4x4 matrix formulation[J].Opt.Soc.Am.,1972,62 (2):502-510.

[10] Wu S T.A Semiempircial model for liquidcrystal refractive index dispersion[J].J.Appl.Phys.,1991,69(4): 2080-2087

[11] Hong T X,Wu S T.Optical wave propagation in a cholesteric liquid crystal using the finite element method[J].Liq.Cryst.,2003,30(3):367-375.

Simulation research on Bragg reflection bandwidth of cholesteric liquid crystal based on Berreman 4×4 matrix

ZHAO Jing,LI Qing-li,XU Li-jun

(Zhangjiakou University,Zhangjiakou 075000,China)

This research simulates the reflection spectrum of cholesteric liquid crystal by Berreman 4× 4 matrix and Matlab program,and analyses the factors that affect the bandwidth of reflection spectrum,such as pitch number(thickness of liquid crystal),refractive index of substrate,birefringence, dispersion of refractive index,fixed pitch,pitch gradient,incident angle and so on.The result illustrates that in order to get an ideal Bragg reflection bandwidth,the thickness of the liquid crystal,the pitch number N,must reach N≥10;The substrate refractive index can impact the maximum reflection,which will be relatively low when the substrate refractive index ngis smaller than the common light reflection and the affection is more obvious as the ngbecomes smaller when ng≥no,a pefect reflection can be attained.The dispersion reflection and big incident angle will make the bandwidth become narrow,while large birefringenceΔn and pitch P lead to broader bandwidth,but the broadening effects is finite.The reflection bandwidth of the pitch gradient cholesteric liquid crystal was simulated theoretically by giving the function expression of pitch gradient,which makes sense for the experimental study of broadband reflection of cholesteric liquid crystal.

O753.2

A

10.3788/YJYXS20153005.0777

1007-2780(2015)05-0777-07

趙靜(1982－),女,河北崇禮人,碩士研究生,講師,研究方向為液晶物理。E-mail:yaya821010＠sohu.com

2015-02-05

:2015-05-08.

?通信聯系人,E-mail:yaya821010＠sohu.com