一類變系數分數階微分方程組的數值解法

李寶鳳，王東華，宗 鵬

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

數學與應用數學

一類變系數分數階微分方程組的數值解法

李寶鳳，王東華，宗 鵬

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

給出了基于Haar小波求解變系數分數階微分方程組的數值方法。首先構造Haar小波得到分數階積分的算子矩陣，利用積分算子矩陣把分數階微分方程組轉換為代數方程組；其次解此代數方程組求得原方程組的數值解；最后舉例說明了所給出的方法的有效性和可行性。

分數階微分方程；Haar小波；算子矩陣；Block Pulse函數

1 Introduction

Fractional calculus is an old mathematical concept dating back to 17th century and involves integration and differentiation of arbitrary order. In 1695, L’ Hospital wrote to Leibniz asking him:“ What if n be 1/2?”. In the following centuries fractional calculus developed significantly within pure mathematics. However the applications of fractional calculus just emerged in last few decades. During the past decades, the field of fractional differential equations has attracted the interest of researchers in several areas including physics, chemistry, engineering and even finance and social sciences[1]. Compared to integer order differential equation, fractional differential equation has the advantage that it can better describe some natural physics processes and dynamic system processes[2]. But mostly fractional differential equations don’t have analytical solutions; there has been significantly interest in developing numerical schemes for their solution. Kai Diethelm has analyzed the fractional differential equations theoretically[3]and mainly studied Volterra integral equations; Changpin Li has studied the numerical algorithm for fractional calculus[4]. All of them, Haar method is the easier one to calculate. Because Haar method can transform the fractional differential equations into a linear system of algebraic equations and there are many zero elements in the coefficient matrix. By now, most of the relevant literatures are about the numerical solution of the fractional differential equations[5-13]and the existence and uniqueness of the solutions for system of fractionaldifferential equations[14], while the research about the numerical solution of the system of fractional differential equations is relatively few.

In the present paper, we intend to use the Haar wavelet method to solve a class of linear system of fractional differential equations as following:

wheret∈［0,T ],0<α,β<1,a,b,canddare known constants, f1( t),f2( t),g1( t) andg2( t)is the functions in the Hilbert spaceL2［0,T ],is fractional derivative of Caputo sense.

The paper is organized as follows. In Section 2, we introduce some necessary definitions and mathematical preliminaries of fractional calculus. In Section 3, after describing Haar wavelet, we derive Haar wavelet operational matrix of the fractional differential equation. In Section 4, the method is defined for approximate solution of the fractional problem (1). In Section 5, a numerical example is given to demonstrate the validity of Haar wavelet method in solving a class of linear system of fractional differential equation. Section 6 comments on the result.

2 Def nitions and notations

We give some necessary definitions and mathematical preliminaries of the fractional calculus theory which are used further in this paper.

Definition 1 The Riemann–Liouville fractional integral operator Iαof order α>0on usual Lebesgue space L1[a,b] is given by

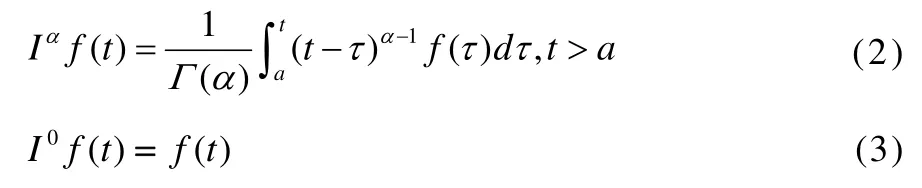
and its fractional derivative of orderα>0 is normally used:

where n is an integer. For Riemann–Liouvilles definition, one has

The Riemann–Liouville derivative has certain disadvantages when trying to model real-world phenomena with fractional differential equations. Therefore, we shall introduce now a modified fractional differential operator D*αproposed by Caputo.

Definition 2 The Caputo definition of fractional differential operator is given by

where n is an integer.

It has the following two basic properties for n-1<α≤n and f∈L1[a,b]

and

3 Haar wavelet and the related operational matrix

3.1 Haar wavelet

The Haar wavelet is the function defined in the Hilbert spaceL2［0,T ]

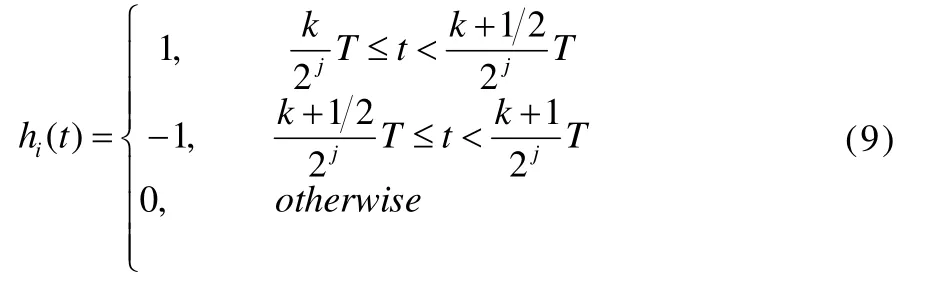
where

andJis a positive integer, thus i=0,1,2,…,m-1, m=2J+1.

Any functionf(t)defined on the interval ［0,T ] can be expanded into Haar wavelet by

where

Iff(t)is approximated as piecewise constant during each subinterval, It may be terminated after m terms, that is

whereCmand H(t)mare m-dimensional column vectors given by

Taking the collocation points as following

We define

3.2 Operational matrix of the fractional integration

The integration of the vectorH(t)

mdefined in Eq. (13)can be obtained as

wherePis the m×moperational matrix for integration[15].

Our purpose is to derive Haar wavelet operational matrix of the fractional integration. For this purpose, we rewrite Riemann–Liouville fractional integration, as following

Now, iff(t)is expanded in Haar wavelets, as showed in Eq.(15), the Riemann–Liouville fractional integration becomes

Thus if tα-1*f(t) can be integrated, then expanded in Haar wavelets, the Riemann–Liouville fractional integration is solved via Haar wavelets.

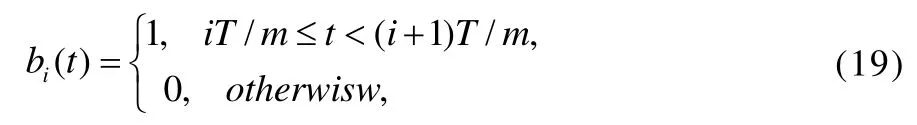
wherei=0,1,2,…,m -1.

The functionsb(t)iare disjoint and orthogonal. That is

From the orthogonality property of BPF, it is possible to expand functions into their Block Pulse series; this means that for every f(t)∈[0,1) we can write

where

so that fifor i=0,1,2,…,m -1are obtained by

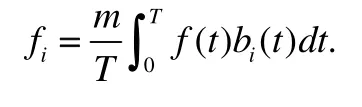
Similarly, Haar wavelet may be expanded into an m-term block pulse functions (BPF) as

We derive the Block Pulse operational matrix of the fractional integrationαFas following

where

with ξ=(2k+1)α-(2k-1)α,k=1,2,…,m -1.

k

Next, we derive Haar wavelet operational matrix of the fractional integration. Let

where matrixαPm×mis called Haar wavelet operational matrix of the fractional integration.

Using Eqs. (23) and (24), we have

From Eqs. (26) and (27) we get

Then, Haar wavelet operational matrix of the fractional integrationis given by

4 Application of Haar wavelet in systemof fractional differential equations

The aim of this paper is to present the numerical solution of the system of fractional differential equations as Eq.(1).

Let

by using Eqs.(8) and (29), we have

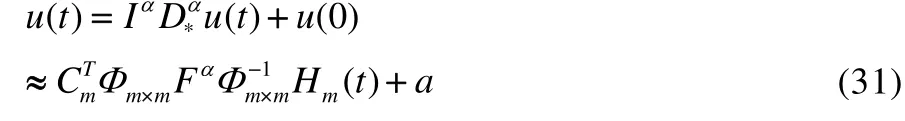
Similarly,

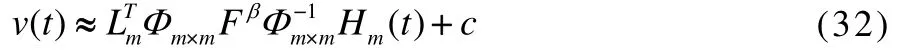
Substituting Eqs.(30), (31) and (1), we have

Thus Eq.(1) has been transformed into a system of algebraic equations. Discrete Eq.(33) at the collocation points defined in Eq.(14), then we have

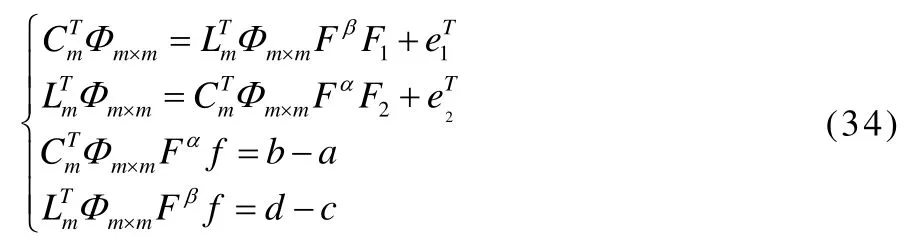
where

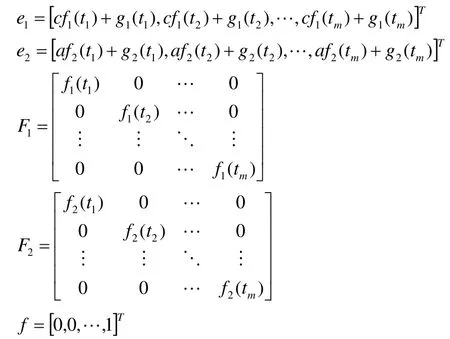
then Eq.(34) can be written as

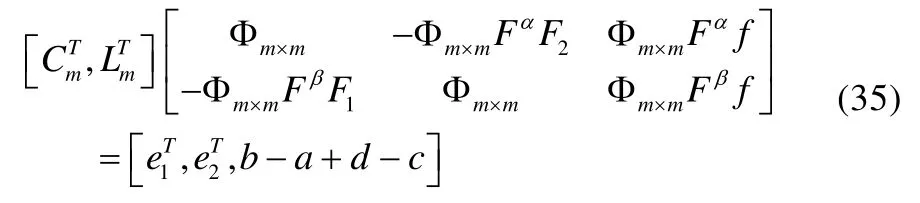
The solutions of the above system which calculated by MATLAB programs can get,. Substituting the values

of the coefficients into Eqs.(31) and (32), we get the approximate solutions of u(t) and v(t).

5 Numerical examples

Consider the following system of linear fractional differential equations

The exact solutions are u(t )=t2-t,v( t)=t2+1. The comparisons between approximate and exact solutions for J=6, T=1 are shown in Fig.1 and for different values of J are shown in Table 1. In the table we can see the accuracy improved when increasing the level of resolution J.

Fig1. The comparison between approximate and exact solutions of Example

Table 1 The comparisons between approximate and exact solutions for different values of J

6 Conclusions

This article adopts Haar wavelet method to solve a class of linear system of fractional differential equations by combining wavelet function with operational matrix of fractional integration. In order to reduce the computation, we transform the initial equations into a linear system of algebraic equations.

Fortunately，there are many zero elements in the coefficient matrix. Efficiency of this method is demonstrated by a numerical example. It is obvious that the accuracy improves when we increase the level of resolution J. Usually, the greater J can reach the higher precision.

[1] Garrappa R, Popolizio M. On the use of matrix functions for fractional partial differential equations[J]. Math. Comput Simulation, 2011, 81(5): 1045-1056.

[2] W Chen, D Baleanu, J A Tenreiro Machado. Preface: Special issue of computers and mathematics with applications on fractional differentiation and its applications[J]. COMPUTMATH APPL, 2010, 59(5): 1585- 1585.

[3] Kai Diethelm, Neville J Ford. Volterra integral equations and fractional calculus: Do neighboring solutions intersect?[J]. Journal of Integral Equations Applications, 2012, 24(1): 25-37.

[4] A Chen, C P Li. Numerical Algorithm for Fractional Calculus Based on Chebyshev Polynomial Approxi- mation[J]. Journal of Shanghai University (Natural Science Edition), 2012, 18(1): 48-53.

[5] Yuste S B. Weighted average finite difference methods for fractional diffusion equations[J]. Comput Phys, 2006, 216(1): 264-274.

[6] Ford N J, Joseph Connolly A. Systems-based decom- position schemes for the approximate solution of multi-term fractional differential equations[J]. Comput Appl Math, 2009, 229(15): 382-391.

[7] Sweilam N H, Khader M M, Al-Bar RF. Numerical studies for a multi-order fractional differential equation. Phys Lett A, 2007, 371(1-2): 26-33.

[8] Rawashdeh E A. Numerical solution of fractional integrodifferential equations by collocation method[J]. Appl Math Comput, 2006, 176(1): 1-6.

[9] Xiuxiu Li. Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method [J]. Commun Nonlinear Sci Numer Simulat, 2012, 17(10): 3934-3946.

[10] Momani S, Odibat Z. Numerical approach to differential equations of fractional order[J]. Comput Appl Math, 2007, 207(1): 96-110.

[11] S Saha ray. On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley Torvik equation[J]. Applied Mathematics and Computation, 2012, 218(9): 5239- 5248.

[12] ü Lepik. Solving fractional integral equations by the Haar wavelet method[J]. Applied Mathematics and Computation, 2009, 214(2): 468- 478.

[13] Yuanlu Li, Weiwei Zhao. Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations[J]. Applied Mathematics and Computation, 2010, 216(8): 2276-2285.

[14] Junsheng Duan, et al. Solution for system of linear fractional differential equations with constant coefficients[J]. J. of Math, 2009, 29(5): 599-603.

[15] Kajani M, Vencheh A. The Chebyshev wavelets operational matrix of integration and product operation matrix[J]. Int J Comput Math, 2008, 86(7): 1118–1125.

（責任編輯、校對：趙光峰）

A Numerical Method for a Class of Linear System of Fractional Differential Equations with Variable Coefficients

LI Bao-feng, WANG Dong-hua, ZONG Peng

(Department of Mathematics and Information Science, Tangshan Normal University, Tangshan 063000, China)

Haar wavelet method is presented for solving a class of linear system of fractional differential equations with variable coefficients. We first construct Haar wavelet and then derive the operational matrix of fractional integration. The operational matrix of fractional integration is utilized to reduce the system of fractional differential equations to a system of algebraic equations. Thus, we get required numerical solutions by solving corresponding system of algebraic equations. In addition, an example is presented to demonstrate the efficiency and accuracy of the proposed method.

fractional differential equations; Haar wavelet; operational matrix; Block Pulse Function

O175.8

A

1009-9115(2015)02-0001-05

10.3969/j.issn.1009-9115.2015.02.001

唐山師范學院科學研究基金項目（2014D09）

2014-03-23

李寶鳳（1971-），女，河北唐山人，碩士，副教授，研究方向為計算數學、運籌學、概率論。 -1-