FV520B不銹鋼銑削穩(wěn)定葉瓣圖的構(gòu)建及實驗*

李宏坤，趙鵬仕，李精忠，董 雷（大連理工大學機械工程學院 大連，116023）

FV520B不銹鋼銑削穩(wěn)定葉瓣圖的構(gòu)建及實驗*

李宏坤，趙鵬仕，李精忠，董 雷
（大連理工大學機械工程學院 大連，116023）

為了提高壓縮機葉輪的加工效率，研究了解析法構(gòu)建銑削穩(wěn)定性葉瓣圖的方法，并利用該方法實現(xiàn)對FV520B材料加工的參數(shù)優(yōu)化。通過該方法可以選取合適的加工轉(zhuǎn)數(shù)和切削深度，避免顫振，使加工后的工件達到要求的精度及表面質(zhì)量，并能夠保護刀具和機床的安全、可靠度。通過實驗數(shù)據(jù)分析，獲取構(gòu)建葉瓣圖的所需參數(shù)，構(gòu)建穩(wěn)定性葉瓣圖，并在所構(gòu)建的葉瓣圖中選取不同測試點，對葉瓣圖進行正確性驗證。研究表明，該方法在實際葉輪加工制造中具有重要意義。

銑削顫振；穩(wěn)定域；模態(tài)分析；FV520B

1 問題的引出

由于葉輪材料的難加工特性，使得加工制造高精度、高質(zhì)量的葉輪成為難題，因此在銑削加工過程中選取合適的切削參數(shù)對于提高加工精度及質(zhì)量具有重大意義。葉輪機械中葉輪是重要的核心工作件，由于要承載工作載荷并適應其較惡劣的工作環(huán)境（高溫高壓），故葉輪的材料選擇條件較為苛刻。FV520B鋼材經(jīng)過熱處理后，可以達到1 100～1 300 MPa的耐壓強度，對大氣及稀釋酸或鹽都具有良好的抗腐蝕能力。這種材料已經(jīng)廣泛用于葉輪制造、航天工業(yè)及其他軍事工業(yè)。圖1為FV520B在五軸加工中心進行葉輪加工。

圖1 五軸加工中心加工葉輪Fig.1 Five-axis center milling impeller

FV520B雖然可以滿足葉輪的要求，但存在難加工的問題。高強度、硬度使得切削過程中切削力大；切削區(qū)局部溫度高，刀具易磨損；韌性和塑性較高，切屑不易折斷分離；它和其他材料親和性強，易產(chǎn)生粘附現(xiàn)象。必須選擇良好的切削參數(shù)才能使加工表面達到精度及質(zhì)量要求。

在切削加工葉輪的時候會因為刀具懸伸量大、精度要求高等因素引發(fā)切削顫振，而避免顫振發(fā)生最有效的方法是使用顫振穩(wěn)定性葉瓣圖。文獻［1］建立了基于切削厚度再生效應的動態(tài)銑削了模型，首先提出了零階解析法（zero-order analytical，簡稱ZOA）。劉強等［2］采用ZOA方法獲得了車削及銑削過程，平頭刀、球頭刀和R刀的穩(wěn)定性葉瓣圖，討論了切削參數(shù)和模態(tài)參數(shù)等對穩(wěn)定性葉瓣圖的影響。

筆者對FV520B的顫振穩(wěn)定域分析進行研究，以獲取最佳的轉(zhuǎn)速，提高切削效率。對動力學模型的優(yōu)化進行了分析，在構(gòu)建葉瓣圖后對其進行實驗驗證，為FV520B加工效率的提高提供技術(shù)支撐。

2 穩(wěn)定性葉瓣圖的構(gòu)建原理

銑削系統(tǒng)可以簡化為二自由度系統(tǒng)，如圖2所示。銑削過程動力學方程［3］可以表示為

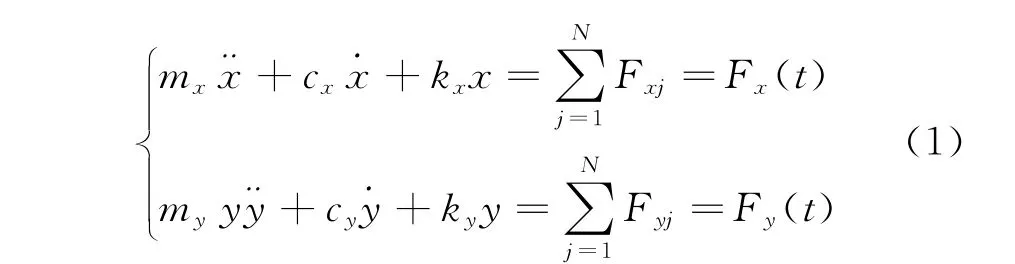
其中，mx，my，cx，cy，kx，ky分別為x，y方向上機床-刀具系統(tǒng)的質(zhì)量、阻尼和剛度；Fxj和Fyj分別為作用在銑刀刀齒j上的切削力在x和y方向上的分量。

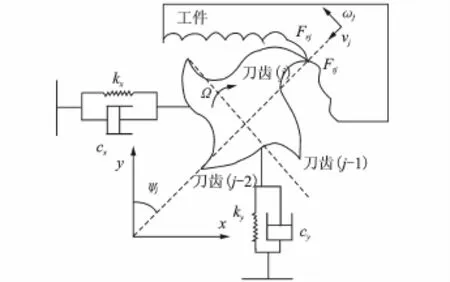
圖2 二自由度銑削系統(tǒng)Fig.2 Two-degree of freedom milling system

在銑削加工中，只考慮再生顫振的動態(tài)切削厚度表達式為

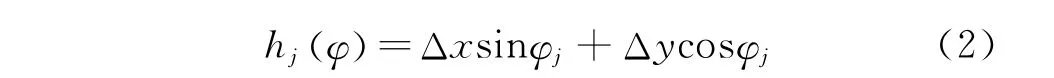
基于Tlusty［4］提出正交切削理論的模型當瞬時角位移為時，作用在刀齒j上的切向和徑向動態(tài)切削力可以表示為

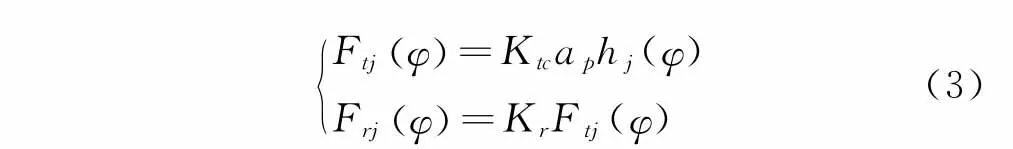
其中：Kr為系數(shù)比，Kr=Krc/Ktc。

將式（2）代入式（3），對各方向上的力求和得到

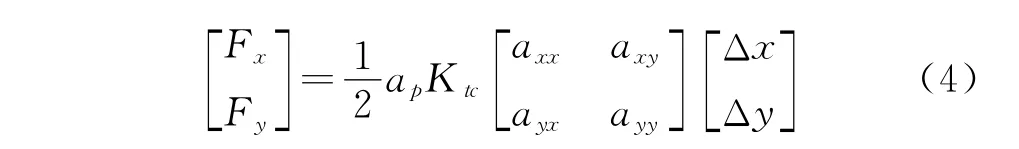
其中：axx，axy，ayx，ayy為方向系數(shù)式。

式（4）可以改寫成矩陣的形式

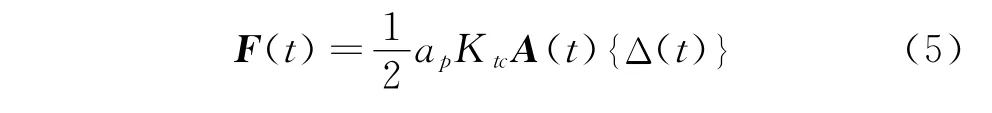
其中：A（t）為與瞬時角位移φj相關(guān)的周期函數(shù)；其角頻率ω=Nn/60；周期T=2π/ω。

對A（t）進行Fourier級數(shù)展開并保留第1項，

則式（5）改寫為

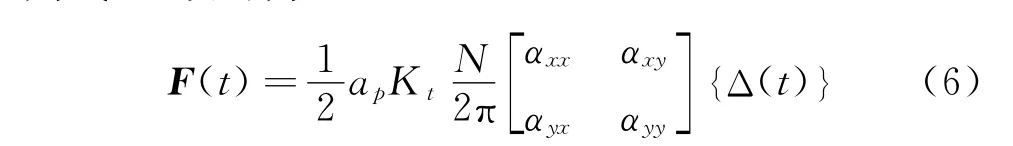
其中：axx，axy，ayx，ayy為平均方向系數(shù)。

通過對式（1）進行整理并進行拉氏變換，其傳遞函數(shù)［3］可表示為

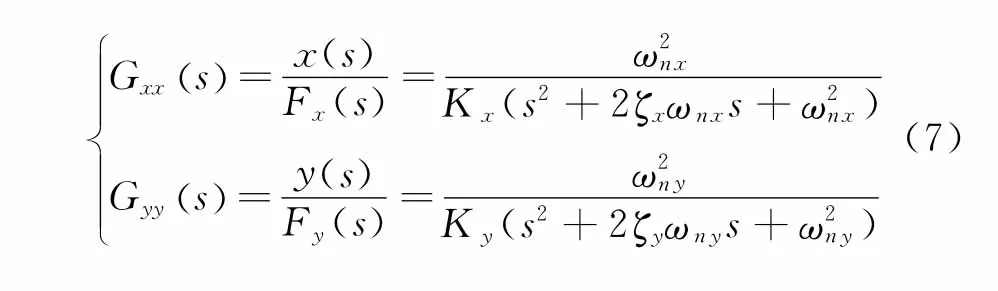
其中：ζx，ζy為阻尼比；ωnx，ωny為系統(tǒng)固有頻率。

系統(tǒng)穩(wěn)定的充要條件是傳遞函數(shù)G（s）特征方程的根均具有負的實部。頻域中切削力可以表示為

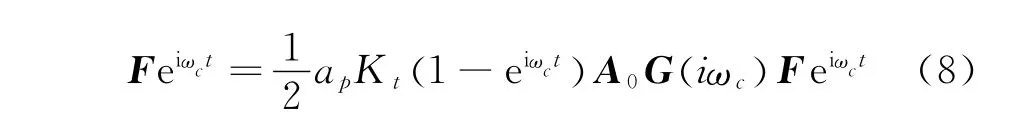
其中：ωc為顫振頻率［5］。

銑削再生顫振頻率下的閉環(huán)反饋系統(tǒng)的特征方程為

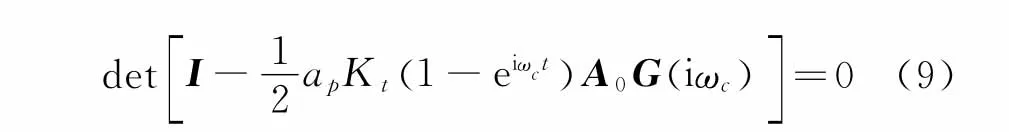
Λ為方程的特征值，其表達式［6］為

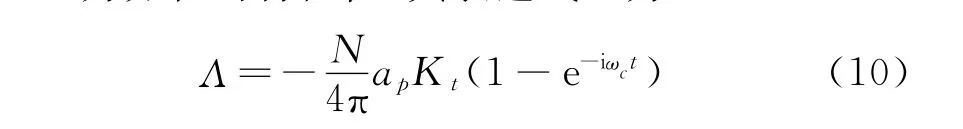
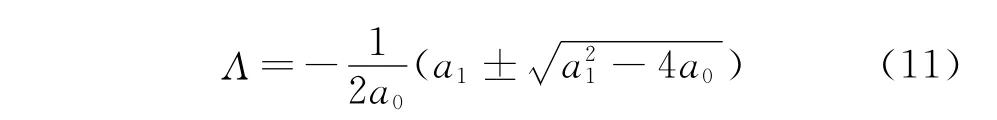
其中：a0=Gxx（iωc）Gyy（iωc）（αxxαyy-αxyαyx）；a1=αxxGxx（ iωc）+αyyGyy（iωc）。

由于G（iωc）中存在虛數(shù)，而切深為實數(shù)，故令Λ =ΛR+iΛI，e-iωct=cosωcT-isinωcT，代入式（10）并令虛部等于零，得

其特征值解析法表示為

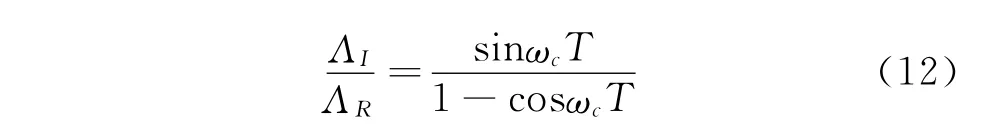
由式（12）和式（10）得到臨界軸向切深［6］為

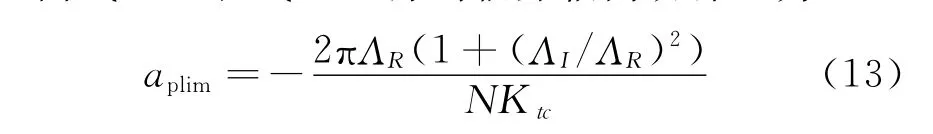
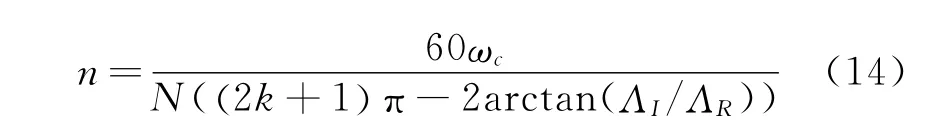
其中：k為葉瓣圖中的葉瓣數(shù)。

從式（13），（14）可知，對于一個給定的機床-刀具-工件系統(tǒng)，只要知道顫振頻率（系統(tǒng)固有頻率附近）、銑刀齒數(shù)、刀具切削系數(shù)和切削系統(tǒng)頻率響應函數(shù)，就能夠計算出軸向臨界切深和相對應的主軸轉(zhuǎn)速，進而可以構(gòu)建出顫振穩(wěn)定性葉瓣圖［7］。

由式（12）得到主軸轉(zhuǎn)速為

3 實驗數(shù)據(jù)采集及分析

3.1 模態(tài)實驗

模態(tài)實驗是通過振動測試來確定系統(tǒng)的固有頻率、阻尼比、剛度和模態(tài)振型，是一種用來分析機構(gòu)動力學特性的方法。模態(tài)實驗在大連理工大學模具所東昱精機CMV-850A加工中心上進行。實驗用刀具為英國斯特拉姆（ATI Stellram）公司生產(chǎn)的7792VXD型牛鼻銑刀（刀片型號為ATI stellram-X500，基質(zhì)為硬質(zhì)合金），刀具直徑為32 mm，懸伸長為200 mm，刀片數(shù)為3個。模態(tài)實驗設備包括：沖擊力錘；加速度傳感器，靈敏度為93 m V/g；NI USB-9234型4通道數(shù)據(jù)采集卡；北京東方振動與噪聲技術(shù)研究所Coinv DASP V10多通道信號采集和實時分析軟件。圖3為模態(tài)實驗的測試裝置示意圖。

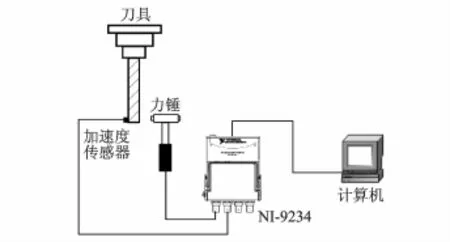
圖3 模態(tài)實驗的測試裝置示意圖Fig.3 Modal experiment test device schematic

采樣參數(shù)設置：采樣頻率為5 120 Hz，采樣點數(shù)為54 576。為了提高模態(tài)測試精度，采用三次錘擊激勵然后求取平均值。圖4為x，y方向的刀具頻率響應曲線。

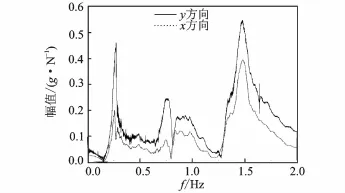
圖4 x，y方向刀具頻響函數(shù)曲線Fig.4 x，y direction frequency response function curve of tool

通過DASP模態(tài)分析軟件提供的Poly LSCF算法，這是一種采用離散時間頻域模型的方法，通過選取合適的階數(shù)和總體擬合，達到所需精度。Poly LSCF算法對于第1階模態(tài)具有特別高的精度，抗干擾能力強，穩(wěn)態(tài)圖清晰，并且易于區(qū)分虛假模態(tài)，運算速度快。由于后n階模態(tài)最后的處理方法相同，影響因子小，并且在最后處理中所得到的穩(wěn)定性葉瓣圖也是取曲線下穩(wěn)定區(qū)域的交集，這里僅以第1階模態(tài)的計算做分析處理。刀具的x，y方向的模態(tài)參數(shù)如表1所示。

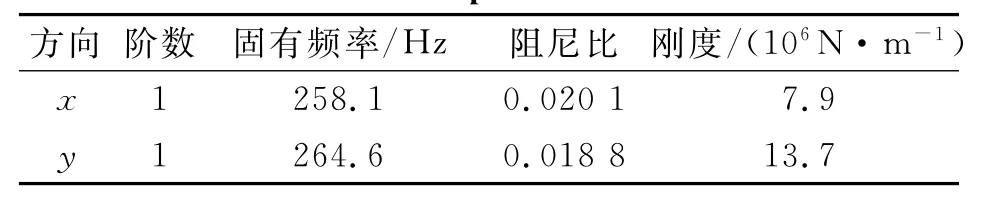
表1 刀具模態(tài)參數(shù)Tab.1 modal parameters of tool

3.2 銑削力實驗

銑削力系數(shù)辨識實驗在大連理工大學模具所東昱精機CMV-850A加工中心上進行，材料為FV520B鋼，刀具型號與模態(tài)實驗相同，測力儀為大連理工大學傳感測控研究所YDX-III97型三向銑削力測試平臺，采樣頻率為20 k Hz。圖5為銑削力測量裝置示意圖。

圖5 銑削力測量裝置示意圖Fig.5 Milling force measuring devices schematic

切削實驗考慮三因素（主軸轉(zhuǎn)速n、切深ap和進給速度f），每個因素3個水平方向按正交表L9（33）設計實驗。正交實驗具有均勻分散、整齊可比的特點，通過交互安排影響實驗因素的參數(shù)進行實驗，達到高質(zhì)量、高精度的實驗結(jié)果，并可以有效節(jié)省實驗的人力、物力和財力［8］。3個因素初步認為影響因子相同，確定的切削參數(shù)見表2。

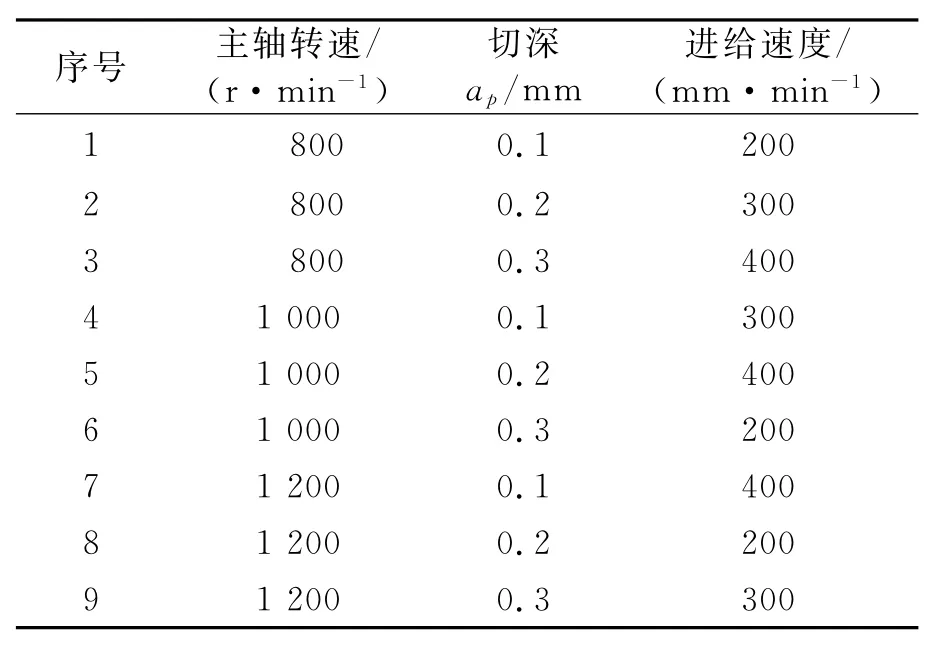
表2 切削參數(shù)Tab.2 Milling parameters

通過Matlab編程計算，將切削力在x，y，z 3個方向上計算平均銑削力大小，其平均切削力測試結(jié)果如表3所示。

通過切削力系數(shù)計算理論及回歸分析，可以計算出6個銑削力系數(shù)［9］。銑削力系數(shù)如表4所示。

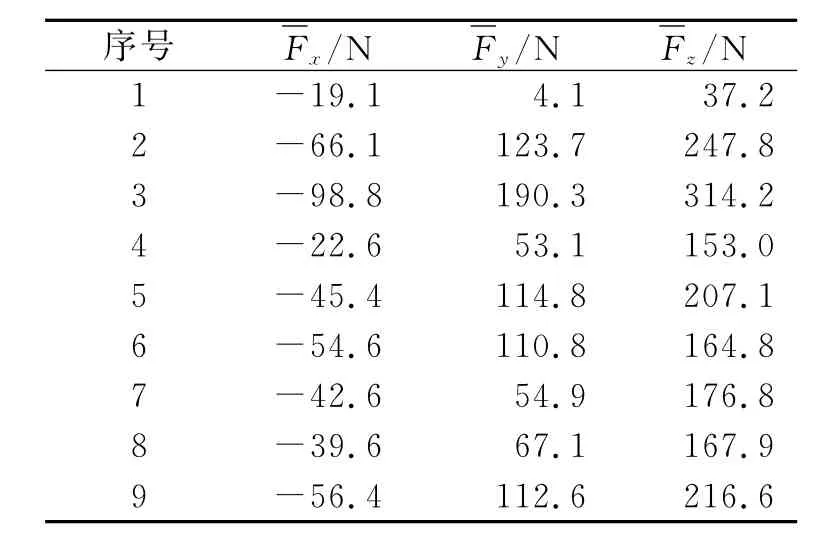
表3 實驗測量平均銑削力Tab.3 Average force from experiment measuring

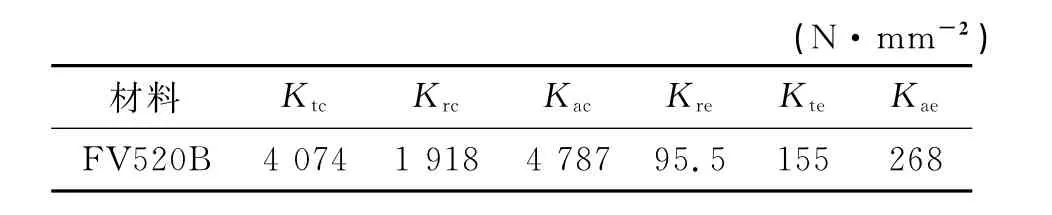
表4 切削系數(shù)Tab.4 Milling coefficient

4 構(gòu)建葉瓣圖及驗證

4.1 葉瓣圖的構(gòu)建

利用模態(tài)分析所得數(shù)據(jù)進行Matlab編程，繪制FV520B鋼材的穩(wěn)定性葉瓣圖如圖6所示。從圖6中可以看出，選擇曲線下方的切削參數(shù)進行加工為穩(wěn)定加工區(qū)域，其中選擇虛線以下部分的切削參數(shù)為絕對穩(wěn)定區(qū)，選擇曲線以上部分的切削參數(shù)進行切削為容易發(fā)生顫振的顫振區(qū)域。根據(jù)葉瓣圖選取合理的加工參數(shù)可以避免顫振，獲得比較高的加工效率、良好的加工表面及精度，并且保護機床與刀具。圖6中在主軸轉(zhuǎn)速500～1 500 r/min之間有較大的穩(wěn)定區(qū)域，在制定切削參數(shù)時優(yōu)先選在該區(qū)域選取，并盡量避免靠近葉瓣圖曲線。

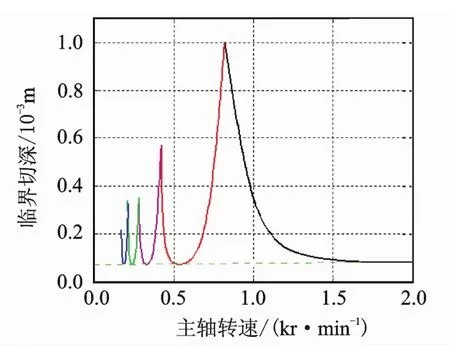
圖6 FV520B鋼銑削穩(wěn)定性葉瓣圖Fig.6 Milling stability lobes of FV520B

4.2 穩(wěn)定性葉瓣圖的驗證

選擇A，B兩點不同的切削參數(shù)進行驗證，圖7中，A處在葉瓣圖的穩(wěn)定區(qū)域，B處在葉瓣圖的顫振區(qū)域，C點處在穩(wěn)定區(qū)域。其中：A，B，C三點的切削參數(shù)如表5所示。

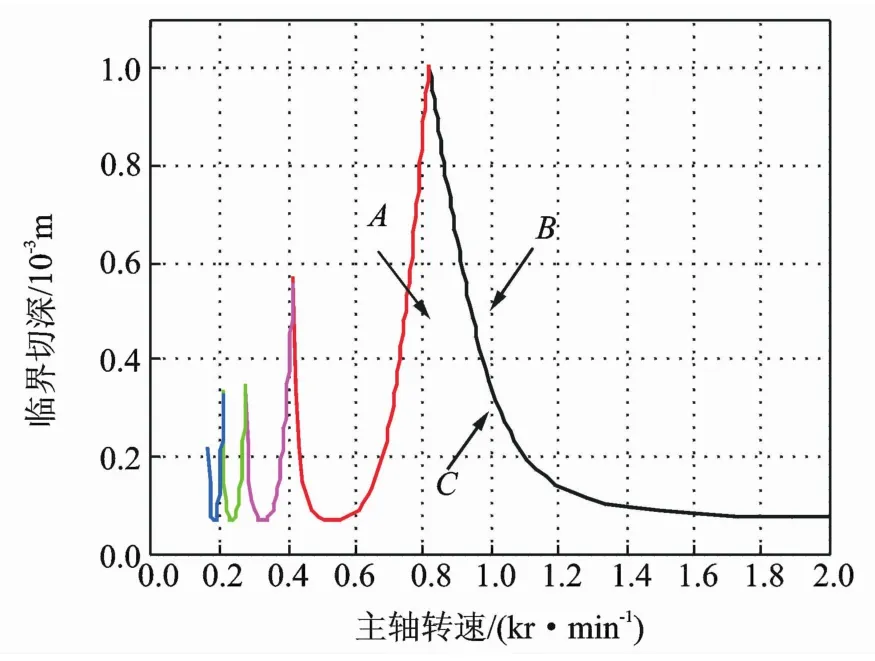
圖7 葉瓣圖中驗證點的選取Fig.7 Verification points selection from lobes

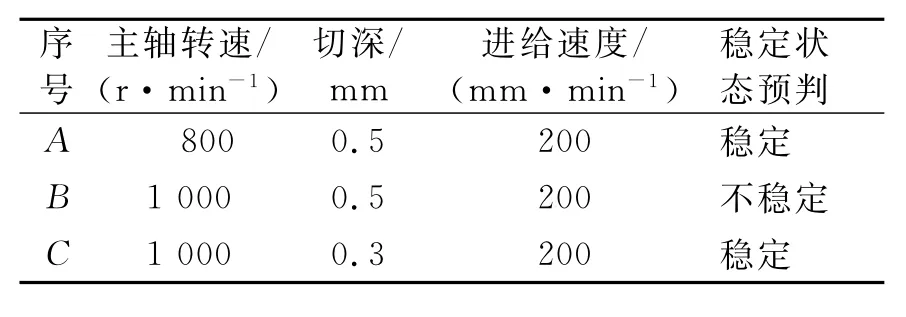
表5 驗證實驗切削參數(shù)Tab.5 Verification experiment milling parameters

穩(wěn)定性的驗證可以通過分析處理力信號來檢測，也可以通過觀察所加工表面的精度及質(zhì)量來區(qū)分。表面質(zhì)量及精度沒有國家標準來區(qū)分是否發(fā)生顫振，而是通過所采集的力信號的分析處理。采用快速傅里葉變換觀察其時域信號及頻域信號的特征，很容易判斷是否發(fā)生顫振［10］。A點力信號數(shù)據(jù)如圖8所示。A點的時域信號平穩(wěn)可靠；頻域信號中，由于刀齒數(shù)N=3，轉(zhuǎn)數(shù)為800 r/min，對應主軸轉(zhuǎn)頻為13.3 Hz，切削頻率為39.8 Hz（13.3 Hz× 3）。振動幅值最大的對應頻率為轉(zhuǎn)頻和切削頻率，沒有出現(xiàn)顫振相關(guān)頻率。B點力信號數(shù)據(jù)如圖9所示。B點的時域信號不好做判斷；在頻域信號中，其主軸轉(zhuǎn)速為1 000 r/min，對應主軸轉(zhuǎn)頻為16.6 Hz，切削頻率為49.8 Hz（16.6 Hz×3）。頻譜圖中幅值最大的頻率為268.6 Hz，與切削系統(tǒng)的固有頻率接近。顫振發(fā)生時，顫振頻率在切削系統(tǒng)固有頻率附近，故選擇在B點切削參數(shù)進行切削，已發(fā)生顫振。

C點力信號數(shù)據(jù)和A點類似，沒有出現(xiàn)顫振相關(guān)頻率，銑削過程是穩(wěn)定切削，與預判斷的結(jié)果一致。證明了筆者所構(gòu)建的銑削穩(wěn)定性葉瓣圖正確可靠。

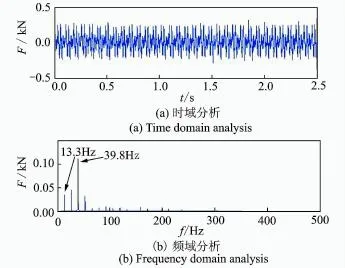
圖8 A點的銑削力信號分析（800 r/min，0.5 mm）Fig.8 Cutting force analysis at A（800 r/min，0.5 mm）

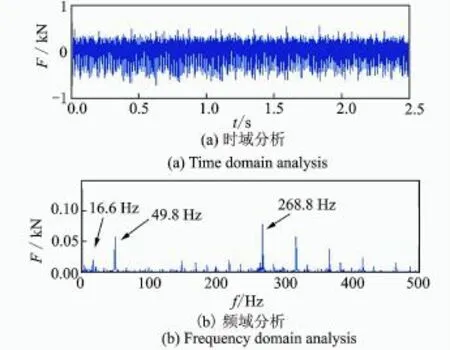
圖9 B點銑削力信號分析（1 000 r/min，0.5 mm）Fig.9 Cutting force analysis at B（1 000 r/min，0.5 mm）

5 結(jié)束語

通過解析法構(gòu)件加工穩(wěn)定性葉瓣圖，對難加工葉輪材料FV520B的實際切削優(yōu)化了切削參數(shù)，使切削顫振現(xiàn)象得到了控制。這也驗證了該方法的正確性和可靠性，提高了加工精度、效率和表面質(zhì)量，保護了刀具及機床的安全。可見，ZOA解析法構(gòu)建葉瓣圖可以避開顫振區(qū)域，簡潔方便，可靠性好，可以推廣應用于其他材料工件的實際加工應用當中。

［1］ Budak A Y.Analytical prediction of stability lobes in milling［J］.CIRP Annals-Manufacturing Technology，1995，44（1）：357-362.

［2］ 劉強，李忠群.數(shù)控銑削加工過程仿真與優(yōu)化-建模、算法與工程應用［M］.北京：航空工業(yè)出版社，2011：70-90.

［3］ 丁燁.銑削動力學-穩(wěn)定性分析方法與應用［D］.上海：上海交通大學，2011.

［4］ Tlusty J，Ismail F.Basic non-linearity in machining chatter［J］.CIRP Ann-Manufacture Technology，1981，30：299-304.

［5］ 李忠群.復雜切削條件高速銑削加工動力學建模、仿真與切削參數(shù)優(yōu)化研究［D］.北京：北京航空航天大學，2008.

［6］ Budak E，Altintas Y.Analytical prediction of chatter stability in milling.part 1：general formulation［J］.Proceedings of the ASME，Dynamics System and Control Division，1995，57（1）：545-556.

［7］ Altintas Y，Ko J H.Chatter stability of plunge milling ［J］.CIRP Annals，2006，55（1）：361-364.

［8］ Xu Zhongan，Wang Tianbao.Brief introduction to the orthogonal test design［J］.Science/Tech Information Development＆amp；Economy，2002，12（5）：148-150.

［9］ Minis I，Yanushevsky T.A new theoretical approach for the prediction of machine tool chatter in milling ［J］.Journal of Engineering for Industry，1993，115：l-8.

［10］吳石，劉獻禮，王艷鑫.基于連續(xù)小波和多類球支持向量機的顫振預報［J］.振動、測試與診斷，2012，32（1）：46-50.Wu Shi，Liu Xianli，Wang Yanxin.Chatter prediction based on continuous wavelet features and multi-class spherical support vector machine［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（1）：46-50.（in Chinese）

TG502.14；TH17

10.16450/j.cnki.issn.1004-6801.2015.04.020

李宏坤，男，1974年9月生，教授。主要研究方向為顫振穩(wěn)定域分析、動態(tài)系統(tǒng)測控和故障診斷。曾發(fā)表《基于KPCA-SCM的柴油機狀態(tài)識別研究》（《振動、測試與診斷》2009年第29卷第1期）等論文。

E-mail：lihk@dlut.edu.cn

*遼寧省科技創(chuàng)新重大專項基金資助項目（201303002）

2013-07-30；

2013-10-09