基于DBNs 的車輛懸架減振器異響鑒別方法

黃海波， 李人憲， 楊 琪， 丁渭平， 楊明亮

(1. 西南交通大學機械工程學院，四川 成都610031;2. 西南交通大學信息科學與技術學院，四川 成都610031)

國內外對減振器異常噪聲的鑒別方法研究較少，還處于起步階段.文獻［1-2］將臺架試驗減振器活塞桿頂端相鄰加速度峰值衰減量作為減振器異響的鑒別指標，取得了一定的效果，但該方法的鑒別準確率不高.文獻［3-4］將臺架試驗減振器活塞桿頂端加速度信號做了功率譜變換，找到減振器異響的主要頻率范圍，以此范圍內的功率譜均方根值作為異響鑒別指標，提高了辨識的準確度，但異響頻段的截取難以準確界定.文獻［5-6］根據減振器工作的特點，將活塞桿頂端加速度信號經過小波變換求出換向沖擊瞬間的特征能量，聚合了減振器異響的信息，鑒別準確度較高，但該方法前期的數據預處理與計算十分復雜，影響了其廣泛應用.

以上減振器異響鑒別方法都是依靠人工經驗提取異響的主要特征，要求工程師對減振器的構造及原理要有深層次的認識，往往需要長時間積累和反復摸索，這是一個不可擴展的途徑［7］. 基于統計模型的BP(back propagtion)神經網絡、邏輯回歸與支持向量機等［8-11］可從訓練樣本中學習獲得統計規律，這些模型雖然可以將原始信號數據作為輸入，但是模型本質上是屬于無隱含層或單隱含層的淺層結構，對數據富含的內在信息提取有限，并且在樣本特征維數較高或者含有大量噪聲的情況下應用受限，所以在多數情況下仍以人工提取特征作為輸入.若能在保證準確率的情況下直接根據傳感器收集的信號對減振器異響進行辨識，這將使鑒別工作變得更加容易，深度學習［12-14］(deep learning，DL)即為此思想奠定了基礎.

深度學習從仿生學的角度模擬人腦進行分析，本質上是含有多層隱含層的神經網絡，但有別于傳統的淺層模型，其實質是通過“逐層初始化”來克服深度模型在訓練上的難度，通過多隱含層來逐級學習數據當中的有用信息，從而提升預測或者分類的正確率.本文開展了減振器整車試驗以及減振器臺架試驗，得出減振器整車與臺架試驗之間的一致性規律，并基于深度學習提出了減振器異響鑒別的新方法.

1 減振器異響試驗分析

1.1 減振器整車試驗

減振器是否異響需要經過專業評審團評價將其量化.首先進行減振器整車道路試驗. 由于減振器異響具有隨機性，常常在車輛低速駛于不平路面時產生，經過大量的整車道路試驗，并考慮消除發動機的噪聲干擾，最終選擇車輛在坡度約為8%的坑洼下坡路面以15 ～20 km/h 的速度熄火空擋滑行.同時，專業評審團隨車進行減振器異響的評價，并測量車內乘員的右耳噪聲和減振器活塞桿頂端振動加速度信號，采樣頻率分別為44 100、2 048 Hz，分辨率為1 Hz，試驗示意如圖1 所示.

圖1 減振器整車道路試驗示意Fig.1 Schematic diagram of shock absorber in the vehicle road test

常用的噪聲評價方法主要有等級評分法和成對比較法.等級評分法根據減振器異響的程度，確定不同的評分等級，將評價人員的全部評分加和求平均的值作為評價指標，其關鍵是評分刻度的確定.由于減振器異響的特殊性，評價選擇3 分制的等級評分法. 將減振器異響分為嚴重異響(評價1 分)、輕微異響(評價2 分)和無異響(評價3 分)3 類，由專業評審團進行評分. 圖2 為減振器活塞桿頂端振動加速度頻譜曲線.由圖2(a)可知，嚴重異響減振器的頻譜曲線在300 ～500 Hz 范圍內幅值最大，輕微異響件次之，無異響件最小，由此可知，減振器異響的強弱可由減振器活塞桿頂端振動加速度信號來刻畫.

1.2 減振器臺架試驗與整車試驗的一致性規律

減振器整車試驗的目的是獲得減振器異響主觀評價，但其存在一致性和可重復性較差的缺點.為了獲得具有統計意義上的結果，并且節約大量的時間和成本，進行了減振器臺架試驗，圖3 為減振器臺架試驗示意. 為了模擬減振器的實際工作狀況，減振器在臺架上的安裝方式與整車相同，并且通過迭代加載實際的路譜作為激振信號，同時采集減振器活塞桿頂端和臺架作動頭的振動加速度信號，采樣設置同減振器整車試驗.

比較圖2(a)、(b)可見，3 種異響程度的減振器樣件都在300 ～500 Hz 范圍內有較好的區分度，其中嚴重異響件的頻譜曲線明顯高于輕微異響件與無異響件，由此可知，減振器異響對于整車試驗與臺架試驗具有一致性規律，即可用臺架試驗代替整車試驗對減振器異響進行鑒別.

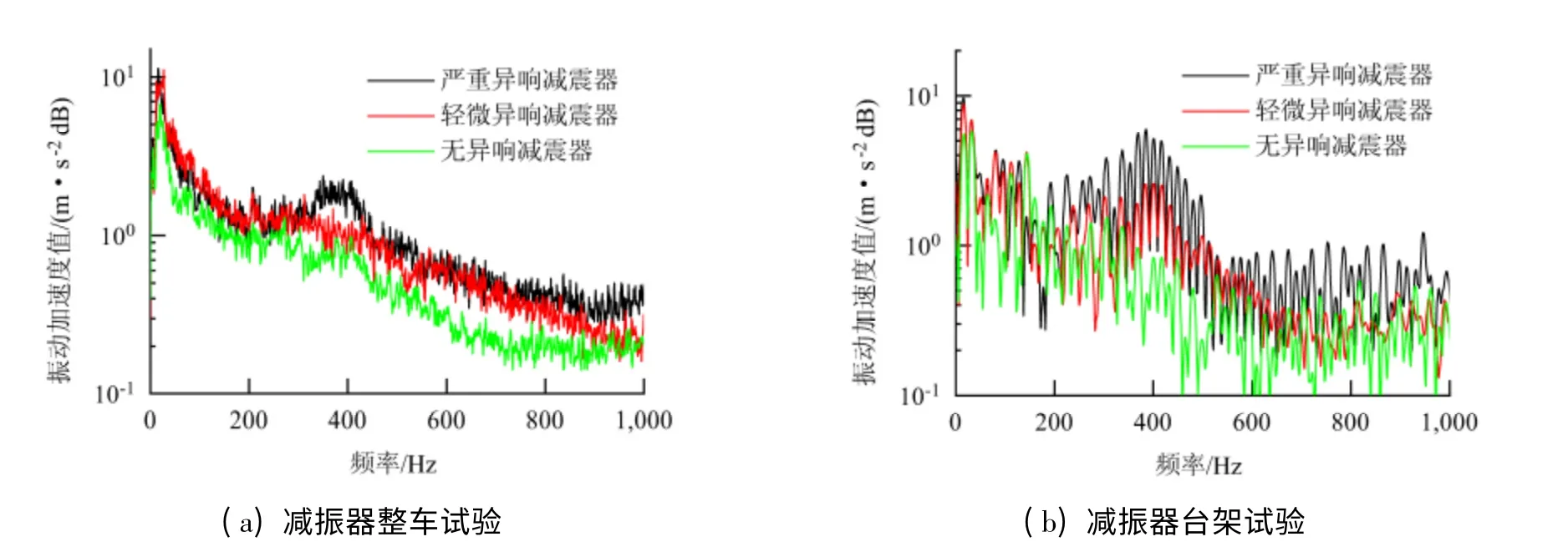
圖2 減振器活塞桿頂端振動加速度頻譜Fig.2 Spectra of piston rod vibration acceleration

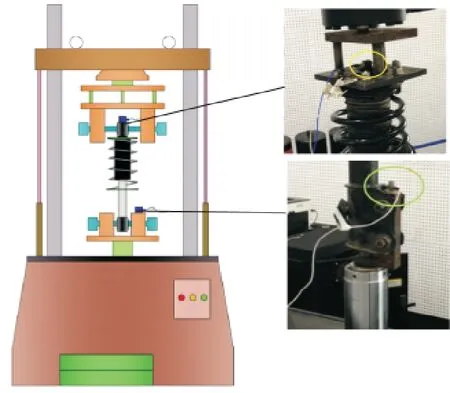
圖3 減振器臺架試驗示意圖Fig.3 Schematic diagram for shock absorber test rig

2 基于深度學習的減振器異響鑒別

2.1 深度學習模型選取及數據樣本采集與預處理

深度學習是機器學習(machine learning)當中的一個新領域［12］，深度學習有兩大經典模型:深度信念網絡(deep belief networks，DBNs)與卷積神經網絡(convolutional neural networks，CNNs). 其中，深度信念網絡的研究和應用最為廣泛，也是本文所采取的方法，具體理論與方法見文獻［12-17］.

減振器異響的鑒別首先采集樣本并建立樣本數據庫.對經過整車試驗的130 支減振器(嚴重異響件21 支，輕微異響件31 支，無異響件78 支)分別進行臺架試驗，收集減振器活塞桿頂端振動加速度信號與臺架作動頭激勵信號，其中，減振器活塞桿頂端加速度信號作為異響鑒別的原始數據，臺架作動頭激勵信號作為后期調整活塞桿頂端加速度信號相位差的輔助信號. 根據深度信念網絡理論［12］可知，樣本的預訓練是一個無監督的特征提取過程，在這樣的條件下適當增加樣本的數目可以更好地提取出減振器異響的本質特征，所以對進行臺架試驗的每一只減振器分別采集10 組信號，每次采集時間為1 s，所采集的這10 組信號評價與其在整車路試中評價得分相同. 然后，根據臺架作動頭激勵信號作為修正相位差的輔助信號，將活塞桿頂端振動加速度信號截斷為同觸發激勵，同相位，長度約為0.2 s(400 個采樣點)的振動信號. 由于深度信念最后的輸出為樣本的聯合概率分布，其值在［0，1］之間，需要對輸入的樣本進行標準化處理，按式(1)對樣本數據進行［0，1］歸一化處理.這樣，樣本數據庫由1 300 個長度為400 個點的歸一化減振器活塞桿頂端加速度信號組建而成.

式中:Xi為樣本數據;

Xmin、Xmax分別為樣本數據的最小值與最大值;

2.2 基于DBNs 的減振器異響鑒別模型

根據深度信念網絡的理論可知，樣本的輸入數據為傳感器收集的信號，為了使結果具有一般性，從樣本數據庫中隨機選取訓練數據和測試數據，并進行深度信念網絡的建模，具體步驟如下:

(1)樣本的選取

構建模型的訓練樣本集{(Xi，Yi)}與測試集{(Xj，Yj)}，其中:Xi為從樣本數據庫中隨機抽取的1 000 個樣本;Xj為剩下的300 個樣本;Yi、Yj分別為每個樣本對應的評價得分.

(2)DBNs 的建立

DBNs 由多個玻爾茲曼機(restricted Boltzmann machine，RBM)堆積而成，由于采用“逐層貪婪訓練方法”進行網絡的訓練，則計算復雜度是線性的，并且DBNs 的深度越深，對原始數據的表達就越抽象.根據數據量的規模和網絡復雜度的影響，將3 個玻爾茲曼機堆積形成的DBNs 作為深度學習模型，如圖4 所示，圖中:可見層V 的輸入是訓練樣本集;h1、h2、h3分別表示第1、第2、第3 隱含層;W 為相鄰的兩層神經元連接權值，并且相鄰兩層神經元與其連接權值構成一個玻爾茲曼機.

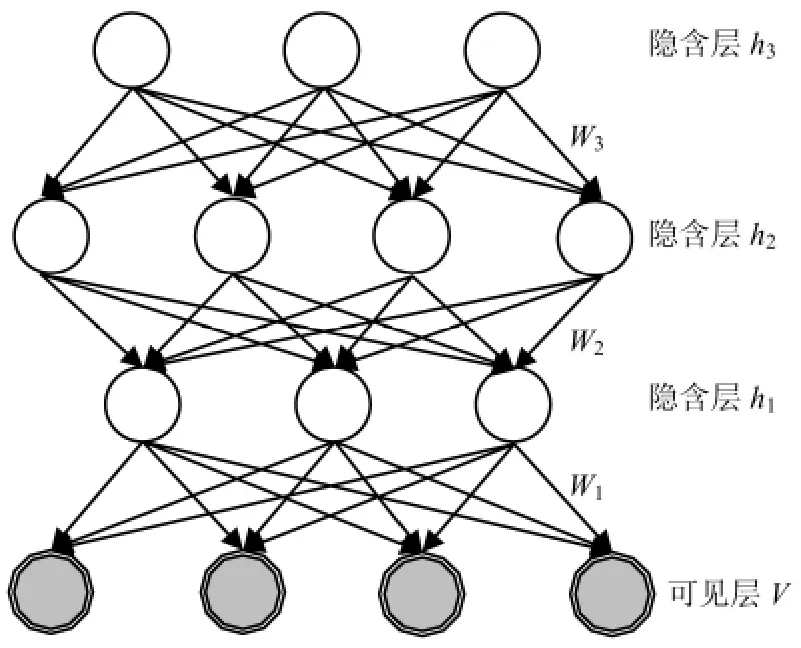
圖4 深度信念網絡拓撲結構Fig.4 Topology of DBNs

由于每一個輸入樣本的長度是400 個點，即樣本為400 維，將可見層V 的神經元個數取為nV=400.隱含層神經元的個數關系到DBNs 的訓練速度與準確度，特別是最頂層的隱含層直接關系到最終的鑒別準確率.但對于隱含層神經元個數的選取尚無理論上的指導，也沒有統一的經驗公式，據目前大量試驗經驗來看，可取nh1=300、nh2=200、nh3取［50，55，…，150］其中之一，因為原始樣本含有大量的噪聲信號，而每一個隱含層又是原始樣本的另外一種表達，逐漸減少隱含層神經元個數的目的就是為了能將減振器異響的主要特征信息逐步提取出來.RBM 重構特征與原始信號的誤差用“重構誤差”來表示，“重構誤差”是根據RBM 的分布進行一次吉布斯采樣后所得到的新特征與原始數據的差異，可用式(2)來表示. 重構誤差能在一定程度上反映RBM 對輸入數據的似然度.

式中:v 為原始數據;

T 為進行重構的迭代次數.

圖5 為訓練數據的重構誤差曲線，可見當nh3取110 時，重構誤差最小，因此，最終建立的DBNs的拓撲結構為400-300-200-110.

(3)DBNs 的訓練

使用的DBNs 模型是在Hinton 所構建的框架［11］下 經 過 次 修 改 而 成，運 行 環 境 為MATLAB2013b.在進行模型訓練之前，需要對模型各參數進行初始化，由于DBNs 可調參數過多，本文僅列出主要參數的設置. DBNs 的主要可調參數有:RBM 學習率、動量項、RBM 初始權重與偏置、RBM 小批量數據容量、RBM 重構迭代次數、DBNs微調次數以及每一層神經單元數目.

圖5 訓練樣本重構誤差隨nh 3 節點數目變化曲線Fig.5 Change of training sample reconstruction error with node number nh 3

RBM 學習率包括權值學習率lw，可見層偏置學習率lbv以及隱含層偏置學習率lbh，學習率過大，將導致重構誤差急劇增加，權重會變得很大，一般取0.005 ～0.200 之間，這里令lw=0.050，lbv=0.100，lbh=0.100.為了彌補學習率過大或過小帶來的問題，引入了動量項，該項可使本次參數更新的方向不完全由當前的梯度方向決定，還結合了上一次參數的更新方向，在某些情況下，可以避免算法在早期陷入局部極值.更新公式為

式中:m 為動量項，在迭代初期令m=0.5，中后期令m=0.9;

wij為可見層單元與隱含層單元的連接權值;

t 為迭代次數.

一般地，連接權重可初始化為正態分布N ～(0，0.1)上的隨機數，可見層單元偏置bi和隱含層單元偏置bj初始化為0.

RBM 使用對比散度［15］進行權重與偏置的更新，若每次基于全部訓練樣本進行，則整體計算量很大，將訓練集和測試集事先分為若干個“小份”，采用分塊的方式來學習可加快計算速度，現將訓練集和測試集設為50 個樣本一份進行分塊計算.RBM 進行1 次權值更新即迭代1 次，設置每層RBM 迭代的次數為100 次.RBM 權值更新完畢后，DBNs 進入微調學習階段，微調是一種監督學習的過程，利用反向傳播算法對整個網絡的權值進行更新，這樣在每一次迭代中，網絡中所有的權重值都可被進一步優化，并且用交叉熵［11］來衡量輸入和輸出概率分布的相似性，交叉熵的定義為

式中:q、p 分別為輸入和重構樣本的概率分布;H(q，p)為交叉熵.

由式(4)可知，交叉熵的值越小，重構的概率分布越接近輸入的概率分布，則隱含層提取的特征越近似原始輸入數據的特征，這里設置DBNs 的微調次數為200 次. 由于每一層神經元的數目在DBNs 建模時已確定，之后可在設置好的參數下對DBNs 進行訓練，所得的交叉熵曲線如圖6 所示.

從圖6 可以看出，在微調達到140 次以后，交叉熵的值基本趨于穩定，表明輸出特征已經是原始數據的另外一種表達.

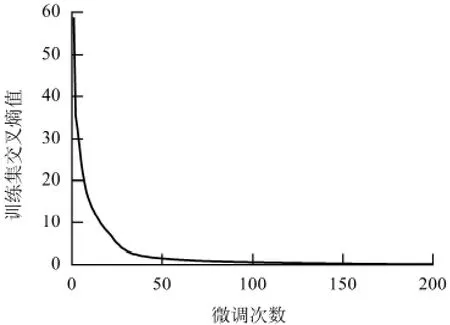
圖6 原始數據逐級特征提取曲線Fig.6 Layer-wise feature extraction curve of original data

圖7 為原始數據DBNs 逐級特征提取曲線，圖中縱坐標為隱含層重構特征.

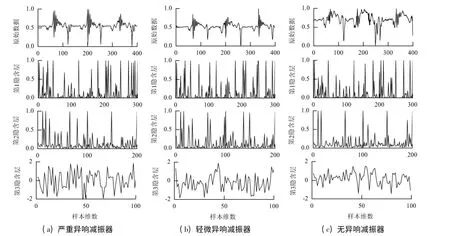
圖7 原始數據DBNs 逐級特征提取曲線Fig.7 Layer-wise feature extraction curve of original data in DBNs

由圖7 可知:(1)隨著隱含層深度的增加，提取的減振器異響特征越來越抽象;(2)嚴重異響減振器的第3 隱含層重構特征比輕微異響減振器第3 隱含層重構特征粗糙，即數據信息變化快速、陡峭，并且輕微異響減振器的第3 隱含層重構特征又比無異響減振器的粗糙，這是由于第3 隱含層數據點中包含了減振器異響的細節信息.最終得到的第3 隱含層重構特征就是原始減振器活塞桿頂端振動加速度信號在低維新空間中的特征表達，并且模型將以此作為減振器異響鑒別的基礎.

2.3 分析結果與對比

利用上述建立好的深度信念網絡模型對樣本數據庫中的測試數據進行鑒別，為了減少隨機選取樣本所帶來的誤差，計算結果取程序運行10 次后的平均值. 圖8 為測試集誤判樣本個數曲線. 由圖8 可知，在微調200 次時，測試樣本最終的誤判數為10 個，并將此結果與經過參數優化的BP 神經網絡、支持向量機及文獻［1-5］中所提的方法進行比較，結果見表1. 表1 中:訓練集中，嚴重異響件樣本149 個，輕微異響件樣本263 個，無異響件樣本588 個;測試集中在嚴重異響件樣本59 個，輕微異響件樣本66 個，無異響件樣本175 個.

由表1 可見，在輸入僅為減振器活塞桿頂端振動加速度信號原始數據的條件下，深度信念網絡模型的異響鑒別準確率達96.7%，并且對于每類異響減振器都有較高的鑒別準確度，而BP 神經網絡和支持向量機模型的鑒別結果不理想.這主要是因為深度信念網絡通過對輸入數據逐級提取從底層到高層的特征，能很好的建立從底層信號到高層特征的映射關系，從而能有效地對減振器異響進行鑒別.然而原始數據的維數較高并且含有大量的噪聲信號，BP 神經網絡和支持向量機很難從中提取出異響的主要特征信息，導致辨識準確度不高. 作為人工特征提取的方法，時域峰值衰減量計算簡單、方便，但鑒別準確率受外界干擾敏感，辨識準確度不高;功率譜均方根值法從頻域的角度對減振器異響信息進行了提取，取得了一定的效果，但鑒別準確率仍不理想;小波特征能量法把焦點集中在減振器活塞桿頂端換向沖擊的瞬間，提取出了異響的主要特征信息，鑒別準確率較高. 以上3 種人工特征提取方法的鑒別效果都不及深度信念網絡方法，然而，由于深度信念網絡模型隱含層較多，所以運行時間相對較長.

圖8 測試集誤判樣本個數曲線Fig.8 Curve of misclassified sample number in the test set

表1 6 種方法鑒別效果對比Tab.1 Comparison of identification results of the six methods

3 結 論

以深度信念網絡為基礎，建立了減振器異響鑒別模型，該模型訓練只需要減振器活塞桿頂端振動加速度信號作為輸入，無需進行人工特征提取，便能逐級提取原始信號當中的有用信息，并且可以較好的適應各種不同的樣本分布，實現了較為一般意義上的異響鑒別. 分析結果表明，當原始信號維數較高且含有大量噪聲的情況下，BP 神經網絡和支持向量機模型效果欠佳，但深度信念網絡模型仍然能夠獲得很高的減振器異響鑒別準確率，并且比傳統的人工特征提取方法效果好，說明了其可行性與實用性.由于該方法具有抗干擾能力強和鑒別準確率高的優點，可為今后大批量、不同型號減振器異響鑒別以及提高鑒別準確度提供新途徑，具有廣泛的工程應用前景.

致謝:西南交通大學研究生創新實驗實踐項目基金資助(YC201402104).

［1］ 舒紅宇，王立勇，吳碧華，等. 液力減振器結構異響發生的微過程分析［J］. 振動工程學報，2005，18(3):

282-287.SHU Hongyu，WANG Liyong，WU Bihua，et al.Analysis on the abnormal structure noise yielding processofhydraulic shock absorber［J］. Journal of Vibration Engineering，2005，18(3):282-287.

［2］ BENAZIZ M，NACIVET S，DEAK J，et al. Double tube shock absorber model for noise and vibration analysis［J］. SAE International Journal of Passenger Cars Mechanical Systems，2013，6(2):1177-1185.

［3］ 宋睿. 汽車雙筒式減振器異響的產生機理與控制方法研究［D］. 成都:西南交通大學，2012.

［4］ 么鳴濤，顧亮，管繼富. 雙筒式減振器異響試驗分析［J］. 工程設計學報，2010，17(3):229-235.YAO Mingtao，GU Liang，GUAN Jifu. Test analysis on the noise of automobile shock absorber［J］. Journal of Engineering Design，2010，17(3):229-235.

［5］ 丁渭平. 汽車底盤系統NVH 及異響控制技術研究［C］∥汽車NVH 控制技術國際研討會. 成都:［s.n.］，2013:93-106.

［6］ 黃海波，李人憲，丁渭平，等. 基于臺架試驗的懸架減振器異響辨識研究［J］. 振動與沖擊，2015，34(2):191-196.HUANG Haibo，LI Renxian，DING Weiping，et al. Rig test for identifying abnormal noise of suspension shock absorber［J］. Journal of Vibration and Shock，2015，34(2):191-196.

［7］ 余凱，賈磊，陳雨強，等. 深度學習的昨天、今天和明天［J］. 計算機研究與發展，2013，50(9):1799-1804.YU Kai，JIA Lei，CHEN Yuqiang，et al. Deep learning:yesterday，today，and tomorrow［J］. Journal of Computer Research and Development，2013，50(9):1799-1804.

［8］ 張建平，胡明華，吳振亞，等. 基于BP 網絡的空中交通管制運行品質評價［J］. 西南交通大學學報，2013，48(3):553-558.ZHANG Jianping，HU Minghua，WU Zhenya，et al.An improved integrated evaluation method on operation performance of air traffic control based on BP network［J］. Journal of Southwest Jiaotong University，2013，48(3):553-558.

［9］ 吳志周，范宇杰，馬萬經. 基于灰色神經網絡的點速度預測模型［J］. 西南交通大學學報，2012，47(2):285-290.WU Zhizhou，FAN Yujue，MA Wanjing. Spot speed prediction model based on grey neural network［J］.Journal of Southwest Jiaotong University，2012，47(2):285-290.

［10］ YOON J，YANG I，JEONG J，et al. Reliability improvement of a sound quality index for a vehicle HVAC systemusing a regression and neural network model［J］. Applied Acoustics，2012，73:1099-1103.

［11］ 秦娜，金煒東，黃進，等. 基于EEMD 樣本熵的高速列車轉向架故障特征提取［J］. 西南交通大學學報，2014，49(1):27-32.QIN Na，JIN Weidong，HUANG Jin，et al. Feature extraction of high speed train bogie based on ensemble empirical mode decomposition and sample entropy［J］.Journal of Southwest Jiaotong University，2014，49(1):27-32.

［12］ HINTON G E，SALAKHUTDINOV R. Reducing the dimensionality of data with neural network［J］.Science，2006，313:504-507.

［13］ BENGIO Y. Learning deep architectures for AI［J］.Foundations and Trends in Machine Learning，2009，2(1):1-127.

［14］ AREL I，ROSE D C，KARNOWSKI T P. Deep machine learning: a new frontier in artificial intelligence research［J］. IEEE Computational Intelligence Magazine，2010，5(4):13-18.

［15］ HINTON G E. Training products of experts by minimizing contrastive divergence［J］. Neural Computation，2002，14(8):1771-1880.

［16］ GRAVES A，MOHAMED A R，HINTON G E. Speech recognition with deep recurrent neura inetworks［C］∥Acoustics，Speech and Signal Processing (ICASSP)，IEEE International Conference. Santa Clara:［s. n.］2013:6645-6649.

［17］ HINTON G E. Training products of experts by minimizing contrastive divergence［J］. Neural Computation，2002，14(8):1771-1880.