列車荷載作用下矮塔斜拉橋索梁振動的相關性

李小珍， 劉楨杰， 辛莉峰， 劉德軍

(西南交通大學土木工程學院，四川 成都610031)

斜拉索作為斜拉橋的主要受力構件，具有剛度小、阻尼較低的特點. 由于斜拉橋主梁質量遠大于斜拉索，在列車或風荷載作用下，主梁、橋塔振動作為激勵將導致斜拉索大幅振動，這種振動稱為索梁相關(耦合)振動［1-2］. 隨著斜拉橋技術的進步，作用在斜拉橋上的車輛荷載越來越大，而列車荷載作為一個長期的動力荷載，若由于橋梁本身特性的原因，使其在車橋動力作用下發生明顯的索梁相關振動，從而導致拉索長期大幅振動，將嚴重影響拉索的耐用性，并對橋梁的安全性造成威脅.

車輛荷載作用下斜拉橋索梁振動的相關性已越來越受到關注，取得了一些研究成果［3-6］. 如Yang Fuheng 等考慮斜拉索振動過程中大位移及索力變化的非線性特性，采用離散索單元建立斜拉索模型，研究了移動荷載作用下主跨150 m 的斜拉橋拉索的非線性振動［3］;張鶴等采用有限元法，通過車橋耦合振動分析，獲得了主梁、橋塔的振動響應，并采用子結構方法提取拉索端點的振動時程研究拉索振動，討論了梁、塔與拉索振動的相關性［4］.研究表明，對于大跨斜拉橋，在斜拉索主要自振頻率范圍內，梁、塔端支點和拉索中點振動頻譜沒有明顯的相關性，在車輛荷載作用下索橋耦合振動的可能性不大［4］.然而，拉索振動響應均包含端部位移響應成分，對斜拉索非線性振動的上述分析并未從斜拉索局部振動特性出發，探討列車通過時斜拉索局部振動與橋梁整體振動之間的相關性.

本文基于列車-線路-橋梁耦合振動理論與動力學模型，以某主跨115 m+95 m 的鐵路矮塔斜拉橋為工程背景，考慮斜拉索與橋梁整體結構之間的相互作用，通過數值積分得到梁體、橋塔振動響應以及斜拉索局部振動響應，探討了不同列車速度下拉索與橋梁整體振動之間的相關性.

1 列車-線路-橋梁耦合振動模型

按照一定的輪軌、橋軌作用關系，將車輛、軌道和橋梁三大子系統組合而成的耦合大系統稱為列車-線路-橋梁耦合振動系統，見圖1.

圖1 列車-軌道-橋梁耦合振動模型Fig.1 Dynamic model of train-track-bridge coupling system

1.1 車輛動力學模型

車輛為二系懸掛四軸車輛(35 個自由度的質量-彈簧-阻尼系統)，包括1 個車體、2 個轉向架和4 個輪對共7 個剛體，每個剛體均考慮橫移、沉浮、側滾、點頭和搖頭5 個自由度，剛體與剛體之間通過彈簧-阻尼元件連接［7-8］. 根據D'Alembert 原理，可推導出車輛各自由度的動力平衡方程，表達式詳見文獻［9］.車輛子系統的運動方程為

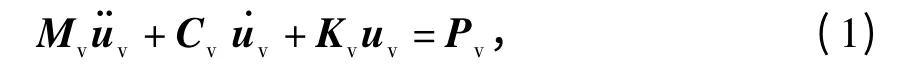
式中:Mv、Cv和Kv分別為車輛子系統的質量、阻尼和剛度矩陣;¨uv、˙uv和uv分別為車輛各自由度的加速度、速度和位移列向量;Pv為軌道子系統作用在車輛子系統上的荷載.

1.2 軌道動力學模型

采用文獻［10］介紹的板式軌道模型模擬無碴軌道結構.橋上板式軌道中，軌道振動主要體現在鋼軌和軌道板的振動上，混凝土底座的作用以參振質量的形式在橋梁動力學模型中加以考慮.考慮鋼軌振動的邊界條件影響后，可將鋼軌的無限長Euler 梁模型簡化為有限長簡支梁模型. 軌道板垂向振動按彈性地基上的等厚度矩形薄板考慮，而橫向可視為剛體運動.軌道子系統的運動方程為

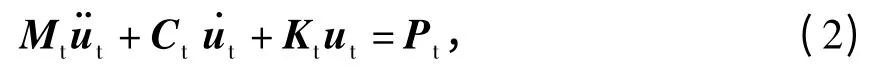
式中:Mt、Ct和Kt分別為軌道子系統的質量、阻尼和剛度矩陣;¨ut、˙ut和ut分別為軌道各自由度的加速度、速度和位移列向量;Pt為車輛和橋梁子系統作用在軌道子系統上的荷載.

1.3 橋梁動力學模型

鐵路矮塔斜拉橋采用空間梁-桿系有限元模型模擬，其中橋塔、主梁采用空間梁單元模擬，斜拉索用空間桿單元模擬.為探討矮塔斜拉橋索梁振動的相關性，分析列車-線路-橋梁耦合振動時，需考慮斜拉索振動的非線性.斜拉索單元的模擬采用與文獻［3］相同的方法，將單根斜拉索離散為多段桿單元，相鄰桿單元鉸接. 斜拉索因自重垂曲引起的非線性效應(采用Ernst 公式)通過折減其彈性模量來考慮;恒載初始內力對結構剛度的影響通過在桿單元剛度矩陣的基礎上疊加幾何剛度矩陣實現［7］.

橋梁邊界條件的模擬方法:墩梁之間的聯結采用主從關系模擬，承臺底采用點彈簧支撐，以模擬承臺底總的基樁約束.橋面二期恒載按均布質量分配于主梁單元.橋梁子系統的運動方程為

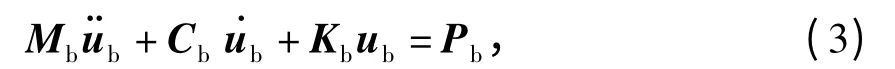
式中:Mb、Cb和Kb分別為橋梁子系統的質量、阻尼和剛度矩陣;¨ub、˙ub和ub分別為橋梁結構各自由度的加速度、速度和位移列向量;Pb為車輛作用在橋梁各自由度上的荷載.

1.4 輪軌、橋軌相互作用關系

若輪軌、橋軌相互作用關系確定，即可由式(1)～(3)用數值積分方法求得各子系統的動力響應.輪軌關系是車輛與軌道子系統聯系的紐帶，包括輪軌接觸幾何關系和輪軌間力的關系. 計算中，假設輪軌剛性接觸，并允許發生脫離，其法相接觸力采用Hertz 非線性彈性接觸理論求解，切向作用力采用Kalker 線性蠕滑理論求解，并通過Johnson-Vermeulen 理論進行非線性修正［8］.橋軌關系是軌道與橋梁子系統聯系的紐帶，包括橋枕間的幾何相容和靜力平衡條件.軌道板位移通過橋梁節點位移插值得到，并由軌道板位移求出作用在其上的橫向力和垂向力.

2 計算條件

2.1 結構概況

以某主跨為115 m +95 m 的客運專線鐵路矮塔斜拉橋為工程背景，總體布置見圖2. 主橋結構為獨塔雙索面預應力混凝土矮塔斜拉橋.橋塔為墩梁塔固結形式，邊跨引橋為簡支梁形式. 索塔在主梁頂面以上結構高27.8 m，實心截面，橫橋向寬2.0 m;斜拉索橫向為雙索面，立面半扇形布置，索塔兩側各9 對斜拉索，塔上索距1.1 m，梁上索距8.0 m，斜拉索在塔頂通過鞍座，兩側對稱錨于梁體;主梁為變高度預應力混凝土連續梁，截面為直腹板單箱雙室結構，中支點梁高7.6 m，跨中及端支點梁高5.0 m;主墩墩身為板式墩，支座為球形支座;塔墩基礎為樁徑2.0 m 的鉆孔灌注樁基礎，邊墩采用樁徑1.5 m 的鉆孔灌注樁基礎.

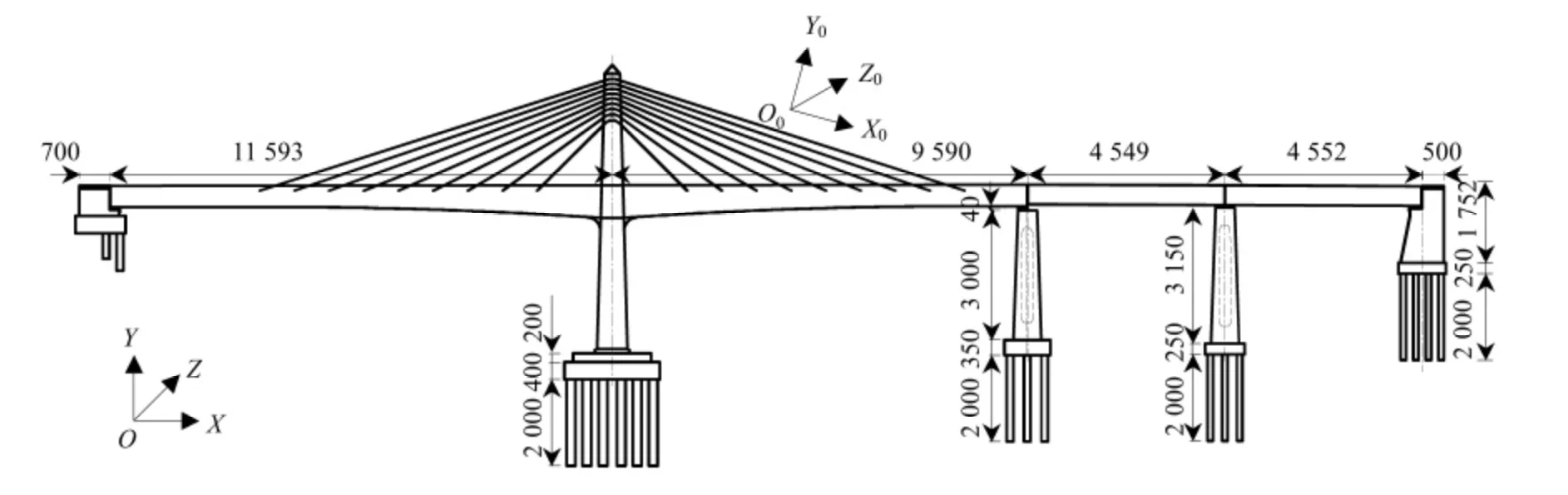
圖2 主橋總體布置(單位:cm)Fig.2 General layout of main bridge (unit:cm)

2.2 計算參數

為研究不同列車速度下索梁振動的相關性，列車模型采用CRH3 動車組，車輛編組為重聯(動車+拖車+動車+動車+動車+動車+拖車+動車)，共16 節，速度分別為225、250、275、300、325 和350 km/h(設計時速范圍).

橋梁阻尼采用瑞利阻尼模式，結構阻尼比取2%，參考頻率分別考慮第1 階和第20 階［11］.

計算時，列車、軌道和橋梁動力響應均不濾波，積分時間步長為0.000 1 s.

3 算 例

3.1 自振特性

根據文獻［12-13］，通過對比全橋振動與拉索振動的計算結果，可初步判斷拉索發生索梁相關振動的可能性.針對全橋整體和斜拉索分別進行自振特性分析，為方便起見，對斜拉索進行編號，見圖3(斜拉索從左至右編號，即橋塔兩側最長的分別為1 號索和18 號索). 表1 和表2 分別給出了全橋(整體)自振頻率和部分斜拉索的自振頻率，圖4為1 號斜拉索的典型模態.

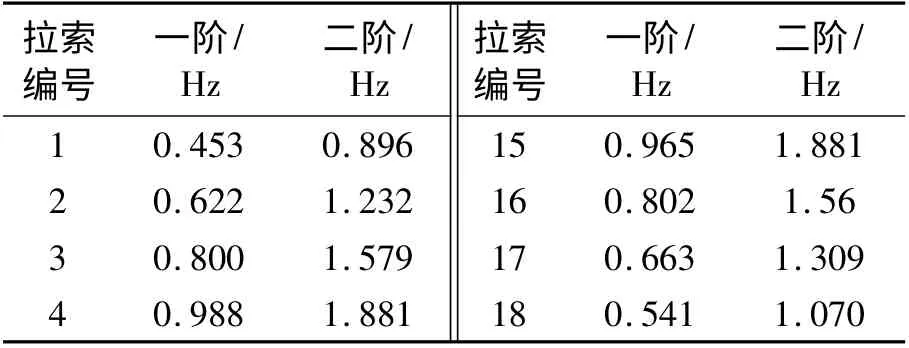
表2 部分斜拉索的自振頻率Tab.2 Vibration frequency of some cables

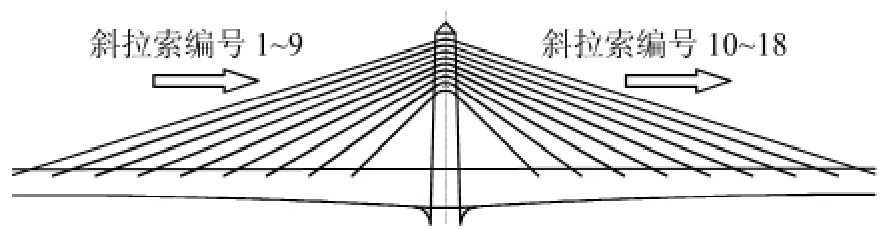
圖3 斜拉索編號Fig.3 The serial number of cables

圖4 1 號斜拉索的典型模態Fig.4 The typical modals of No.1 cable

3.2 斜拉索局部振動

斜拉索兩端點分別連接在橋塔和主梁上，在列車荷載作用下，主梁和橋塔發生振動，從而激勵斜拉索振動，而斜拉索局部振動直接引起拉索索力變化.故對斜拉索在列車荷載作用下的響應，應重點關注其局部振動.

圖2 中，OXYZ 為總體坐標系，O0X0Y0Z0為斜拉索局部坐標系(X0方向與各拉索軸向平行).由式(3)，采用Newmark-β 法可求得橋梁系統的動力響應，即可得到拉索在整體坐標系下的位移響應.而要得到其局部振動響應，可將扣除端點位移后的斜拉索響應向Y0和Z0方向投影(程序中通過坐標轉換矩陣得到拉索局部振動響應).

在列車荷載作用下，梁體、橋塔主要在XY 平面內振動，斜拉索也主要受到X0Y0面內的端點激勵.經計算，拉索在Z0方向的局部振動位移幅值遠小于Y0方向，故分析列車荷載作用下索梁振動的相關性時，主要分析OXY 面內的橋梁振動響應，并取斜拉索中間節點的響應作為拉索局部振動分析對象.

3.3 不同列車速度下橋梁的動力響應

考察CRH3 動車組以225 ～350 km/h 的速度通過橋梁時梁體、橋塔的動力響應規律. 圖5 為CRH3 動車組以350 km/h 的速度通過橋梁時主梁第1 跨跨中位移響應時程及其位移響應頻譜曲線，表3 給出了不同列車速度下梁體、橋塔位移響應幅值和位移頻譜的分析結果.

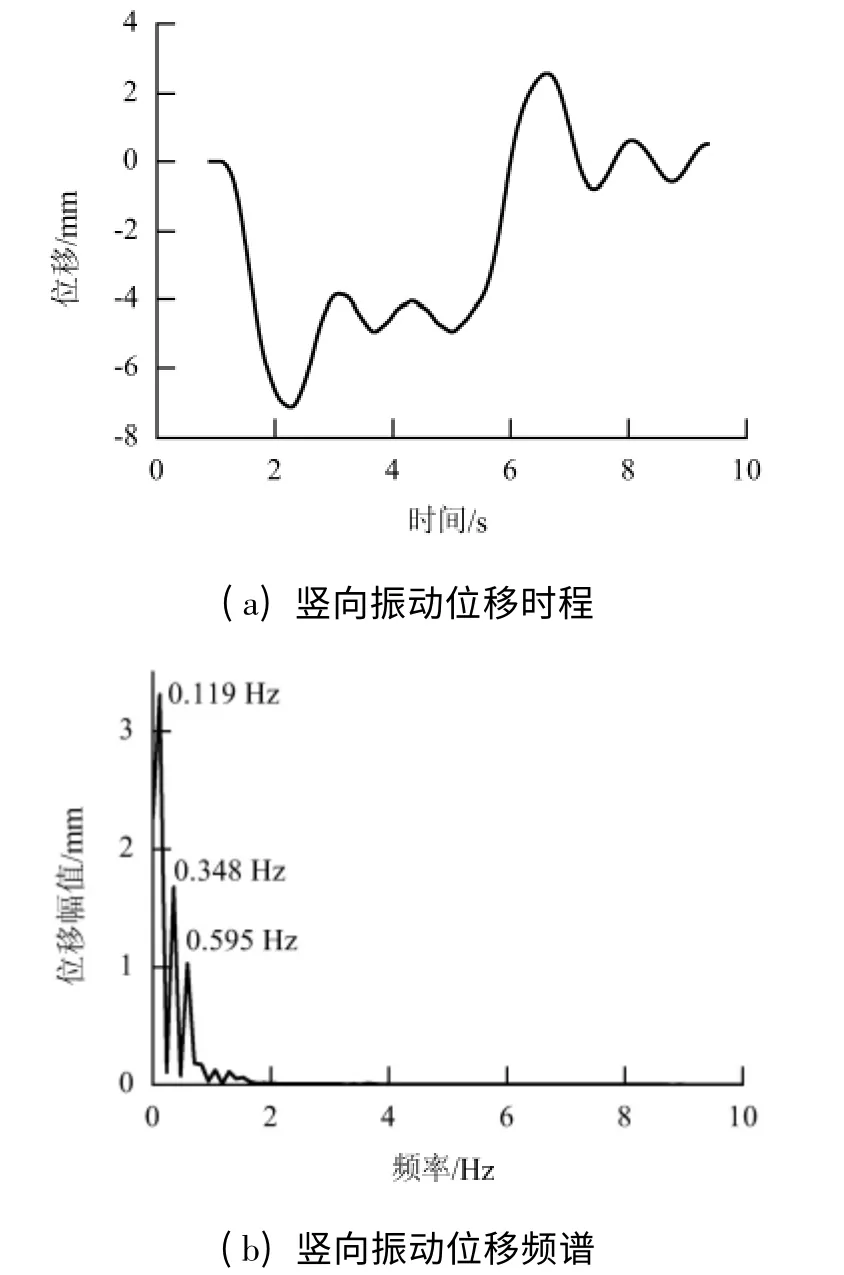
圖5 主梁第1 跨跨中位移時程和頻譜Fig.5 Displacement time history and frequency spectrum of the first span

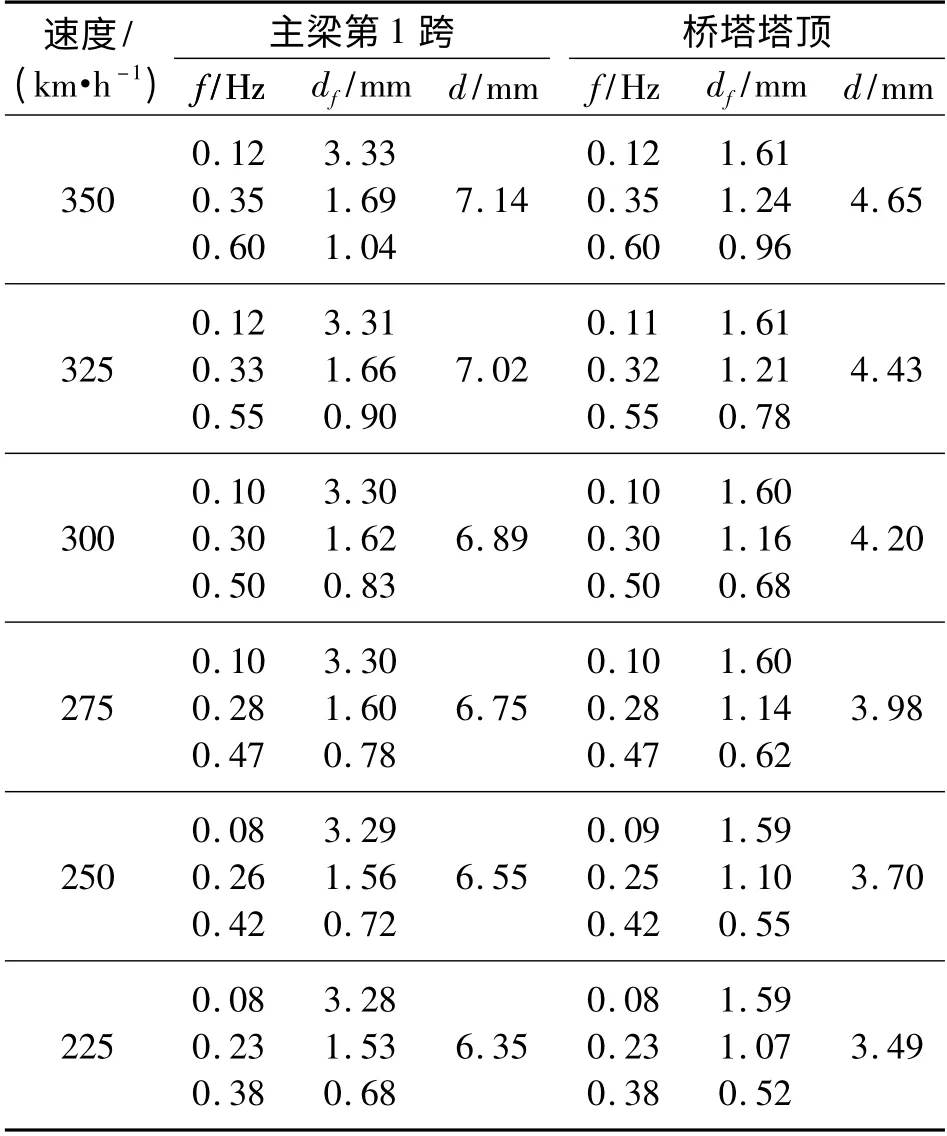
表3 不同列車速度下主梁、橋塔的動力響應Tab.3 Dynamic responses of main beam and pylon vs. train running speed

從 圖5 和 表3 可 見，CRH3 動 車 組 以225 ～350 km/h 的速度運行時，主梁、橋塔振動包含的主要頻率以低頻為主. 隨主要頻率值增大，其對應的位移幅值減小，且主要頻率值均小于全橋整體一階自振頻率(0.78 Hz)，表明主梁、橋塔振動包含的主要頻率為列車經過橋梁時的等效激勵頻率;主梁、橋塔位移響應和響應幅值包含的主要頻率及其對應的位移幅值均隨列車速度提高而增大. 其中，位移響應對列車速度不如頻率敏感，這主要是由于位移響應受振動頻率對應的位移幅值控制.

從表3 可見，頻率對應的位移幅值越大(頻率值占振動頻率的比重越大)，受列車速度影響越小.

圖6 為CRH3 動車組以225 ～325 km/h 的速度經過橋梁時1 號斜拉索的局部振動位移時程和位移響應頻譜曲線，表4 給出了不同列車速度下斜拉索的局部振動位移響應和位移頻譜的分析結果.

從圖6 和表4 可見，與主梁和橋塔相比，斜拉索局部振動頻率分布更集中，且其振動位移響應和響應幅值包含的主要頻率和頻率幅值均對列車速度較敏感.

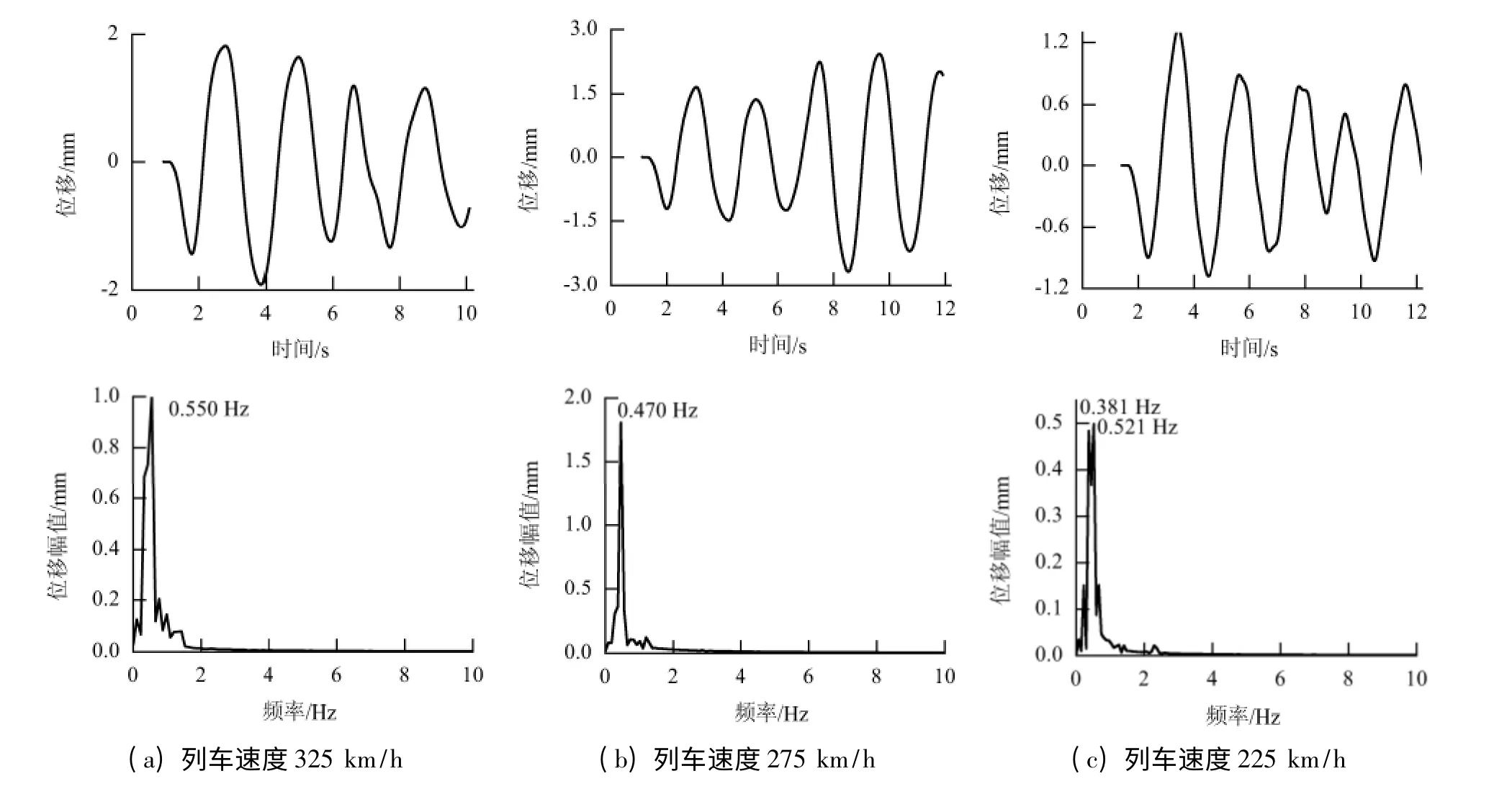
圖6 1 號斜拉索局部振動位移時程和頻譜Fig.6 Displacement time history and frequency spectrum of No.1 cable

比較表3 和表4 中振動主要頻率與拉索自振頻率可知，斜拉索局部振動包含的主要頻率是與拉索自振頻率最接近的斜拉索端點位移激勵頻率——梁體、橋塔振動包含的頻率成分(列車速度為225 ～275 km/h 時，2 號和17 號斜拉索局部振動包含的主要頻率也為端點激勵頻率，因所占比重小，表3 中未給出).

從主梁和橋塔動力響應的分析結果可知，位移響應受列車速度影響較小，而拉索局部振動位移響應對車速較敏感(表4).這主要是由于斜拉索振動源于拉索端部梁體、橋塔的位移激勵，而梁體、橋塔激勵頻率主要由列車速度控制，且當激勵頻率與拉索自身基頻非常接近時，將引起斜拉索共振，從而導致拉索振動位移增大. 如CRH3 動車組以275 km/h 的速度運行時，1 號拉索局部振動位移響應大于列車以325 ～350 km/h 的速度運行時.而比較頻率幅值，列車速度275 km/h 時的頻率值0.47 Hz 對應的梁體、橋塔激勵頻率幅值小于列車速度325 ～350 km/h 時的頻率值0.60、0.55 Hz 對應的梁體、橋塔激勵頻率幅值. 由此可判定1 號斜拉索產生了共振(與列車速度225 和325 km/h 相比，列車速度275 km/h 時斜拉索的局部振動響應幅值并未迅速衰減，反而增大，見圖6). 當拉索長24 ～85 m，直徑118.71 ～129.87 mm 時，在列車荷載作用下，其局部振動位移幅值小于3 mm.

目前，斜拉索振動控制要求的容許振幅等于拉索直徑或等于索長的1/1 700 ～1/300［14］.可見，雖然部分拉索產生了共振，但振動位移幅度較小. 實際上拉索產生索梁相關振動導致大幅共振的現象較少見［1］，這主要受拉索阻尼的影響［2，15］.

表4 不同列車速度下斜拉索的局部振動響應Tab.4 Local vibration responses of cables vs. train running speed

4 結 論

基于列車-線路-橋梁耦合振動理論與動力學模型，以某主跨115 m+95 m 的鐵路矮塔斜拉橋為工程背景，考慮索與橋梁整體結構之間的相互作用，研究了列車以不同速度(CRH3 動車組，速度為225 ～350 km/h)通過橋梁時，斜拉索振動與橋梁整體振動之間的相關性. 研究表明，當列車在設計時速范圍內通過橋梁時:

(1)全橋振動包含的主要頻率為列車的等效外激勵頻率，其值小于全橋一階振動頻率，未引起全橋發生一階及一階以上大幅振動.

(2)全橋振動包含的主要頻率和振動位移幅值均隨列車速度提高而增大.振動位移響應幅值受各振動頻率對應的位移幅值控制，其對列車速度的變化不如頻率敏感;在列車荷載作用下，斜拉索局部振動源于拉索端部主梁、橋塔位移激勵(全橋振動)，故斜拉索局部振動位移響應和響應幅值包含的主要頻率和頻率幅值均對列車速度較敏感.

(3)斜拉索局部振動包含的主要頻率為與拉索自振頻率最接近的斜拉索端點位移激勵頻率，說明列車荷載作用下索梁振動的相關性問題實質上是一個能量傳遞過程，當拉索端點位移激勵頻率與其自振頻率接近時，能量易于在索梁間傳遞.

(4)當列車荷載的等效外激勵頻率與斜拉索自振頻率接近時，斜拉索在外激勵作用下會發生共振，但共振幅值不大(斜拉索局部振動位移幅值小于3 mm).

致謝:西南交通大學揚華之星資助項目.

［1］ 王濤，沈銳利，李洪. 斜拉橋索-梁相關振動概念及其研究方法初探［J］. 振動與沖擊，2013，32(20):29-34.WANG Tao， SHEN Ruili， LI Hong. Primary exploration for concept and studying method of cablebeam vibration in a cable-stayed bridge［J］. Journal of Vibration and Shock，2013，32(20):29-34.

［2］ 龍俊賢，熊濤. 斜拉橋索梁耦合振動研究［J］. 交通科技，2012(5):27-30.LONG Junxian，XIONG Tao. Research on cable-beam coupled resonance of cable-stayed bridge［J］.Transportation Science and Technology，2012(5):27-30.

［3］ YANG Fuheng，FONDER G A. Dynamic response of cable-stayed bridges under moving loads［J］. Journal Engineering Mechanics，1998，124(7):741-747.

［4］ 張鶴，謝旭. 車輛荷載作用下大跨度斜拉橋鋼和CFRP 拉索的非線性振動［J］. 工程力學，2009，26(8):123-130.ZHANG He，XIE Xun. Nonlinear vibration of steel and CFRP cables of long span cable-stayed bridge under vehicular loads［J］. Engineering Mechanics，2009，26(8):123-130.

［5］ DAS A，DUTTA A，TALUKDAR S. Efficient dynamic analysis of cable-stayed bridges under vehicular movement using space and time adaptivity［J］. Finite Elements in Analysis and Design，2004，40(4):407-424.

［6］ 謝旭，朱越峰，申永剛. 大跨度鋼索和CFRP 索斜拉橋車橋耦合振動研究［J］. 工程力學，2007，24(增刊):53-61.XIE Xu，ZHU Yuefeng，SHEN Yonggang. Study on vibration of long-span cable-stayed bridge with steel and CFRP cables due to moving vehicles［J］. Engineering Mechanics，2007，24(Sup.):53-61.

［7］ 李小珍，劉德軍，晉智斌. 大跨度鐵路懸索橋車-線-橋耦合振動分析［J］. 鋼結構，2010，25(12):6-12.LI Xiaozhen，LIU Dejun，JIN Zhibin. Analysis of traintrack-bridge coupled vibration of a railway long-span suspension bridge［J］. Steel Construction， 2010，25(12):6-12.

［8］ 雷虎軍，李小珍，劉德軍. 地震作用下高墩剛構橋行車安全性分析［J］. 地震工程與工程振動，2014，34(5):87-93.LEI Hujun，LI Xiaozhen，LIU Dejun. Train running safety analysis of high-pier rigid frame bridge under earthquake action［J］. Earthquake Engineering and Engineering Dynamics，2014，34(5):87-93.

［9］ 翟婉明，夏禾. 列車-軌道-橋梁動力相互作用理論與工程應用［M］. 北京:科學出版社，2011:32-43.

［10］ 王橋川. 大跨度鋼桁拱橋行車安全性分析［D］. 成都:西南交通大學土木工程學院，2011.

［11］ 李小珍，雷虎軍，朱艷. 車-軌-橋動力系統中Rayleigh阻尼參數分析［J］. 振動與沖擊，2013，32(21):52-57.LI Xiaozhen，LEI Hujun，ZHU Yan. Analysis of Rayleigh damping parameters in a dynamic system of vehicle-track-bridge［J］. Journal of Vibration and Shock，2013，32(21):52-57.

［12］ 成水生. 大跨度斜拉橋拉索的振動及被動、半主動控制［D］. 杭州:浙江大學建筑工程學院，2002.

［13］ 楊素哲，陳艾榮. 超長斜拉索的參數振動［J］. 同濟大學學報:自然科學版，2005，33(10):1303-1308.YANG Suzhe，CHEN Airong. Parametric oscillation of super-long stay cables［J］. Journal of Tongji University:Natural Science，2005，33(10):1303-1308.

［14］ 曾智勇. 橋面激勵下斜拉索振動及其抑振研究［D］. 哈爾濱:哈爾濱工業大學土木工程學院，2010.

［15］ 陳丕華，王修勇，陳政清，等. 斜拉索面內參數振動的理論和試驗研究［J］. 振動與沖擊，2010，29(2):50-53.CHEN Pihua，WANG Xiuyong，CHEN Zhengqing，et al. Theoretical and experimental study on parametric oscillations in a stayed-cable［J］. Journal of Vibration and Shock，2010，29(2):50-53.