M型流量計的數值模擬與數字化標定
崔配配 賈清泉 劉 博 李寶寬
(1.東北大學材料與冶金學院,沈陽 110819;2.遼寧聚焦科技有限公司,沈陽 110041)
目前,流量測量技術在工業領域中得到了廣泛應用。但在非標準流量計的研究中,由于管道或工況復雜,急需一種測量精度高、儀表系數線性度穩定的流量計,因此M型差壓式流量計作為一種在穩定性及測量精度等方面表現良好的流量計,成為了應用極為廣泛的流量計之一。在此,筆者建立了M型流量計的數學模型,仿真計算了不同管徑管道下M型流量計的各壓力參數,研究其在復雜管道中的應用情況和穩定性,以提高M型流量計在實際管道應用中的防堵塞性能。
M型流量計屬于差壓式流量計的一種。對于差壓式流量計,節流件的選取直接影響流量計的性能[1]。M型流量計主要由迎流面和背流面兩組取壓管道組成(圖1)。在裝置的上游產生高壓區,下游產生負壓區,從而產生穩定的壓差。

圖1 M型流量計的幾何結構
2 數值模擬計算
計算介質采用可壓縮空氣,應用Gambit軟件對幾何模型進行網格劃分,使用基于有限體積方法的Fluent軟件進行計算。利用 Fluent數值仿真指導流量計的設計與優化已經成為研究流量儀表的一種很好的方法[2]。計算所采取的湍流模型為標準k-ε模型,采用Simple算法對壓力和速度進行耦合[3]。同時,為了更加貼近實際工況,考慮了粘度及密度等物性的變化。
2.1 數學模型
2.1.1主要控制方程
連續性方程為:

動量方程為:

能量方程為:
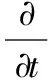
2.1.2湍流模型
標準k-ε湍流模型的魯棒性非常好,適用于一般情況下的流場模擬,是應用最廣泛的湍流模型之一,其包括了渦粘度系數、湍動能及其耗散率等因素,對湍流的長度、尺度和湍流速度進行計算求解,是渦粘性發展起來的最簡單和完備的二方程模型[4]。
湍動能k和耗散率ε的輸運方程為:
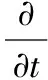
Gk+Gb+ρε-YM+Sk

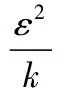
湍流粘度求解方程為:
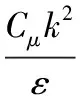
模型常數C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3。
2.2 網格劃分與計算分組
使用Gambit軟件對流體域進行網格劃分,網格為結構化網格和非結構化網格的組合,網格量約150萬。網格劃分情況如圖2所示。
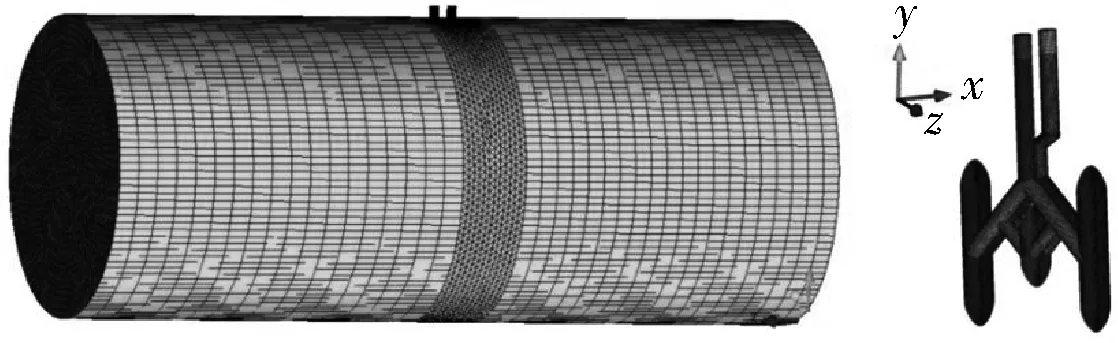
圖2 網格劃分情況
分別計算直徑為500、600、700、800mm的管道,并且每組分別計算速度v=3i+3,Δv=3m/s(i=0,1,2,…,9)的工況。
2.3 結果分析
M型流量計為非標準流量計,其測量裝置系數K是流量計性能的重要參數[5],標定測量裝置系數K非常重要,其計算式為:

式中K——測量裝置系數;
Δp——壓差,Pa;
ρ——流體的密度。
通過數值模擬計算,分別讀出各組正壓p1、負壓p2和壓差值Δp,進而計算出4組不同管徑管道在不同速度下的測量裝置系數K及其相對誤差δ(表1~4)。觀察其線性度,4組管道的裝置系數K的相對誤差最大值分別為3.20%、1.17%、2.12%和1.38%,這表明裝置系數K在4組管道內均有良好的線性度,完全達到工程應用的要求。
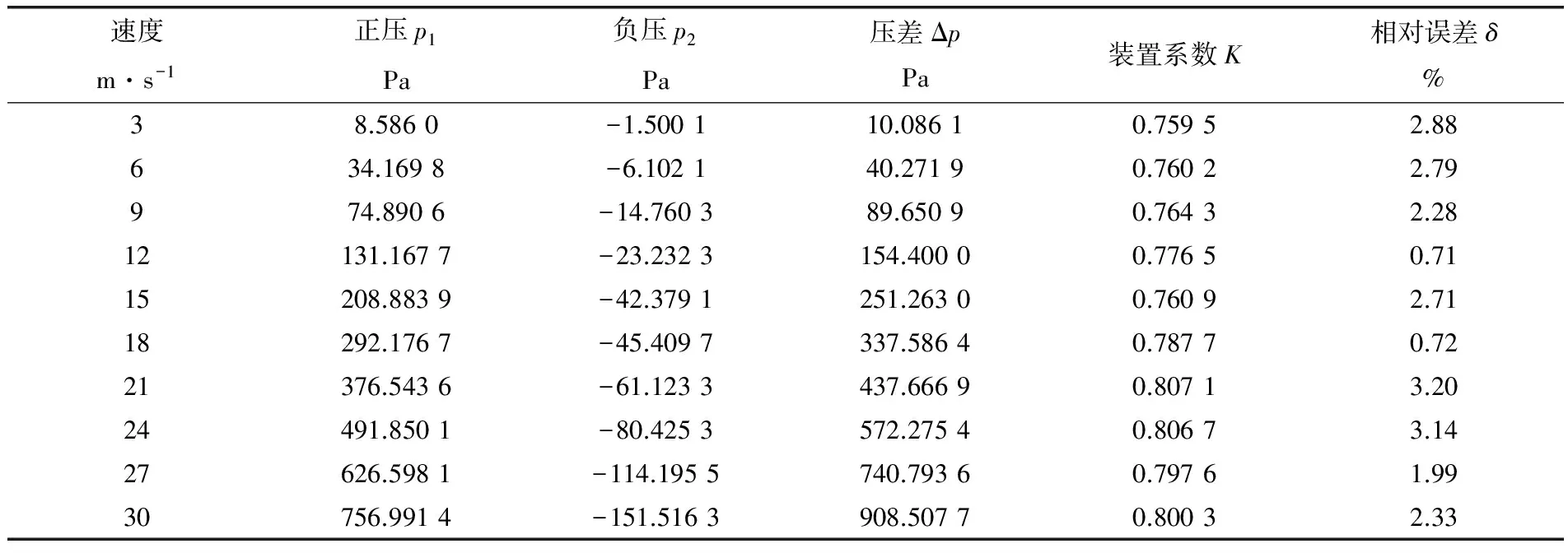
表1 D=500mm管道在不同速度下的性能參數
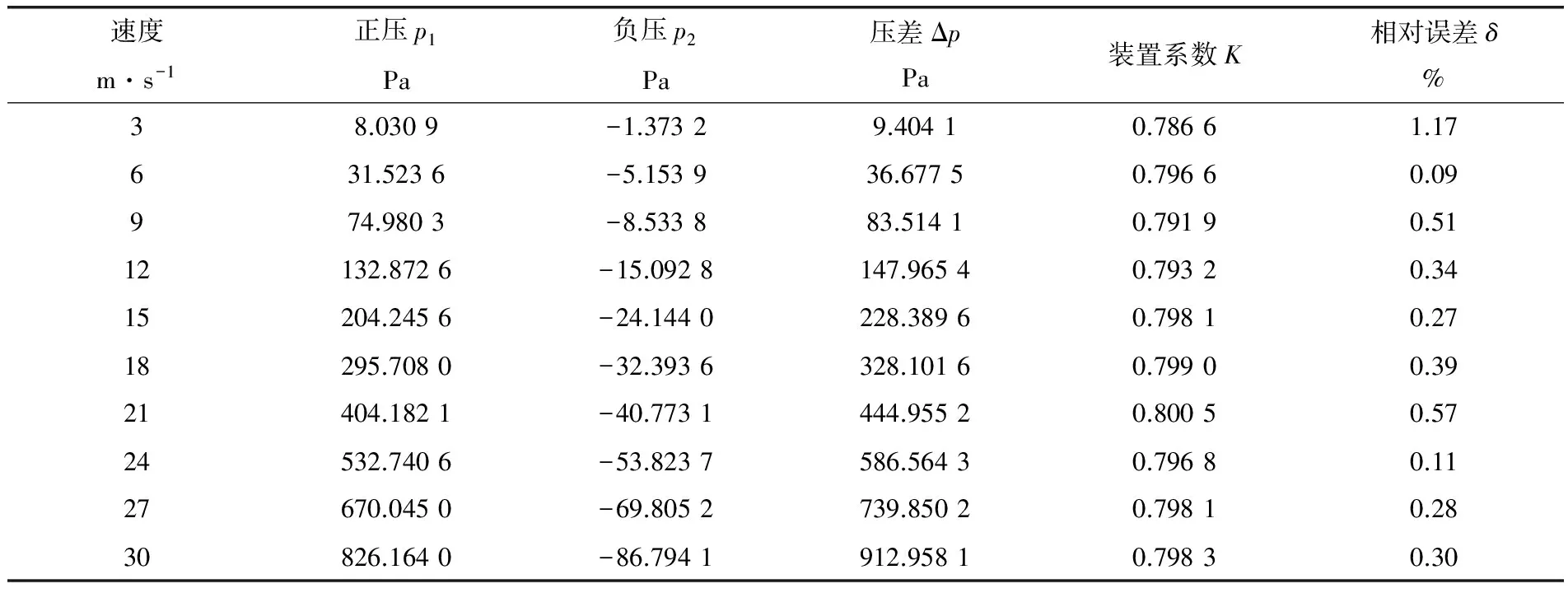
表2 D=600mm管道在不同速度下的性能參數
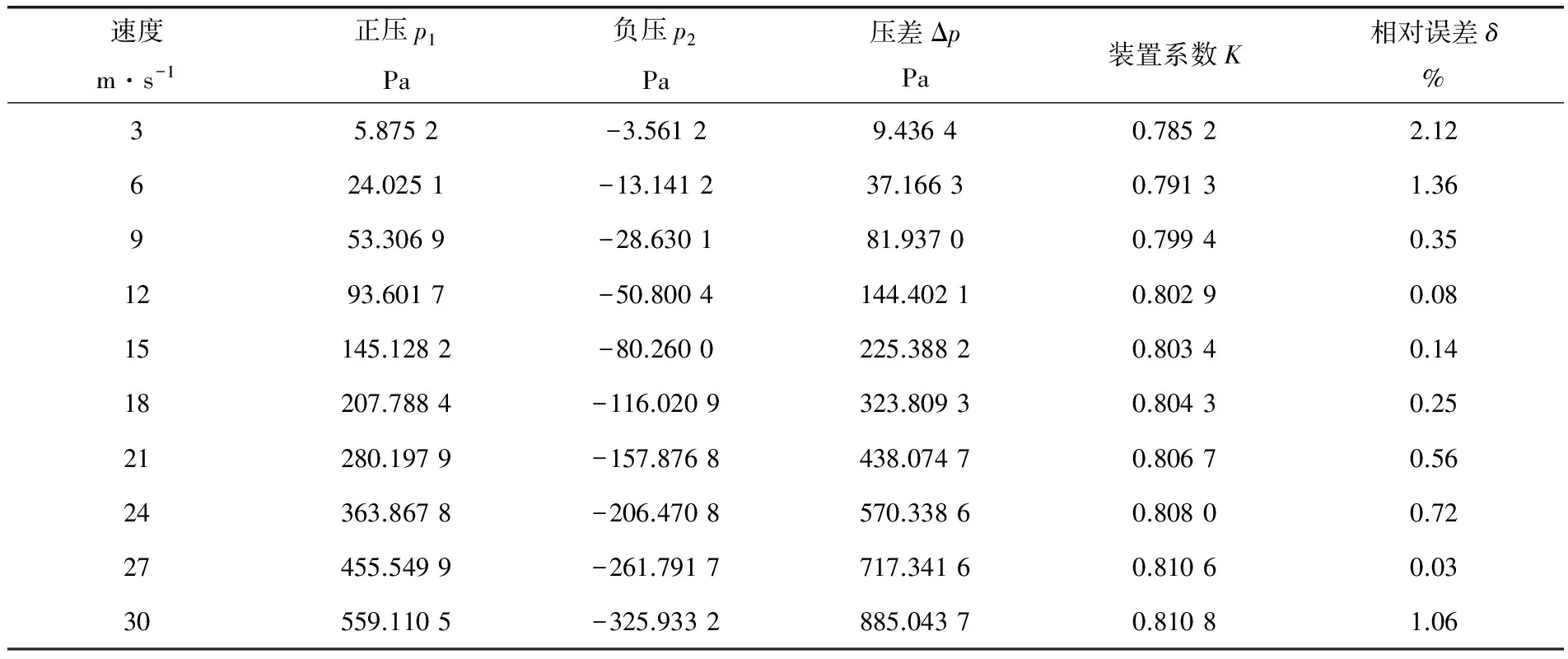
表3 D=700mm管道在不同速度下的性能參數
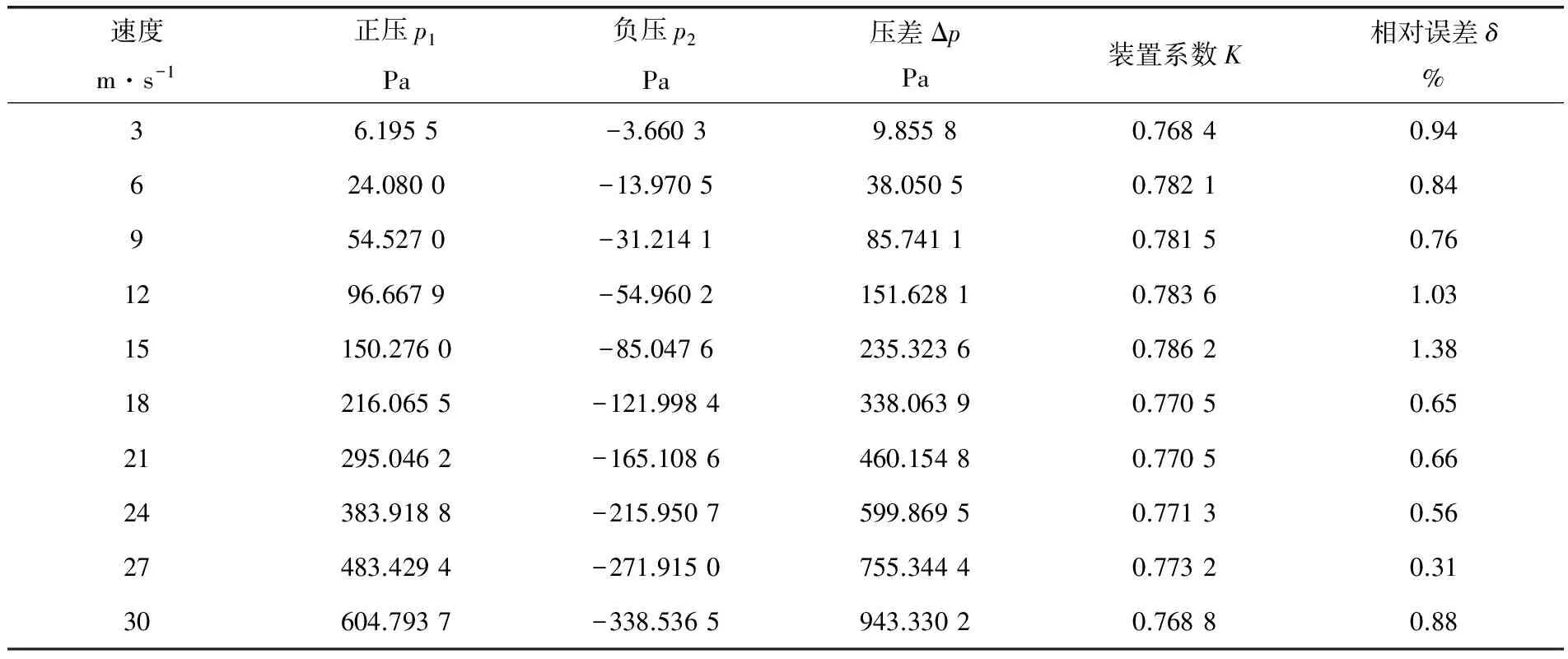
表4 D=800mm管道在不同速度下的性能參數
不同管徑管道的流量計壓力參數曲線如圖3所示,正負測壓點的曲線開度隨速度的增加而增加,即壓差隨速度的增加而逐漸變大。并且,隨著管徑的增加,壓差的增大也更加明顯,也就是說,此類M型流量計在大管徑管道中的應用性能更加突出。
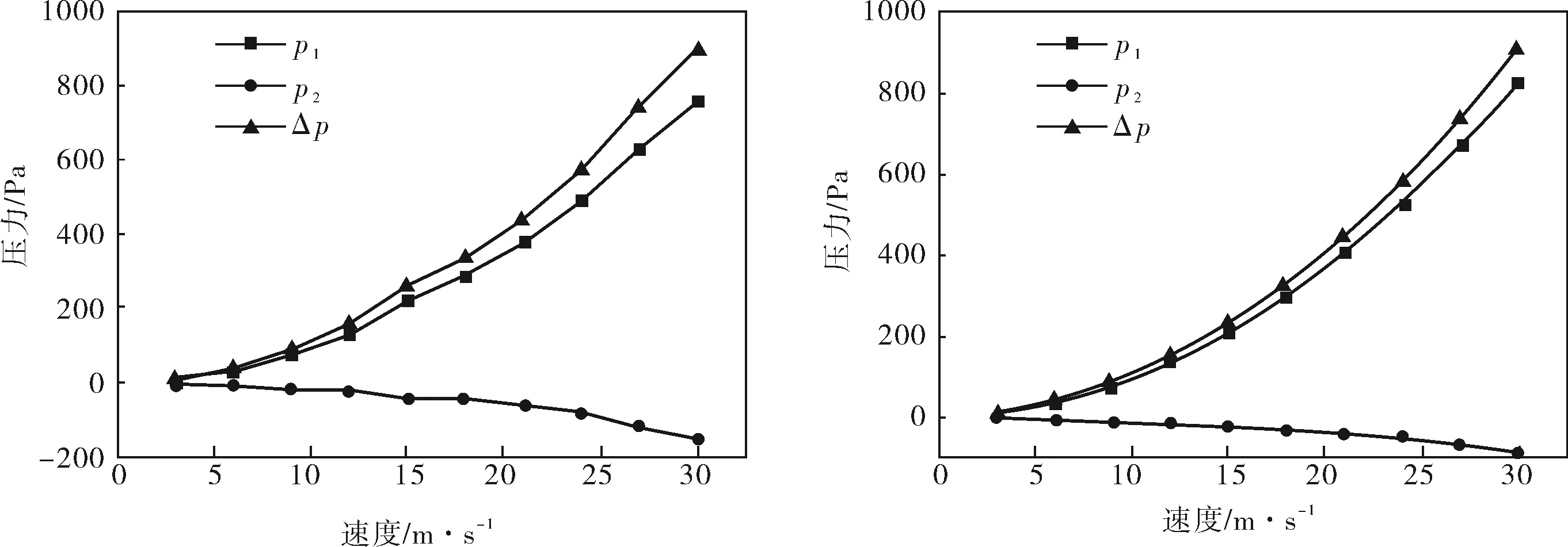
a. D=500mm b. D=600mm
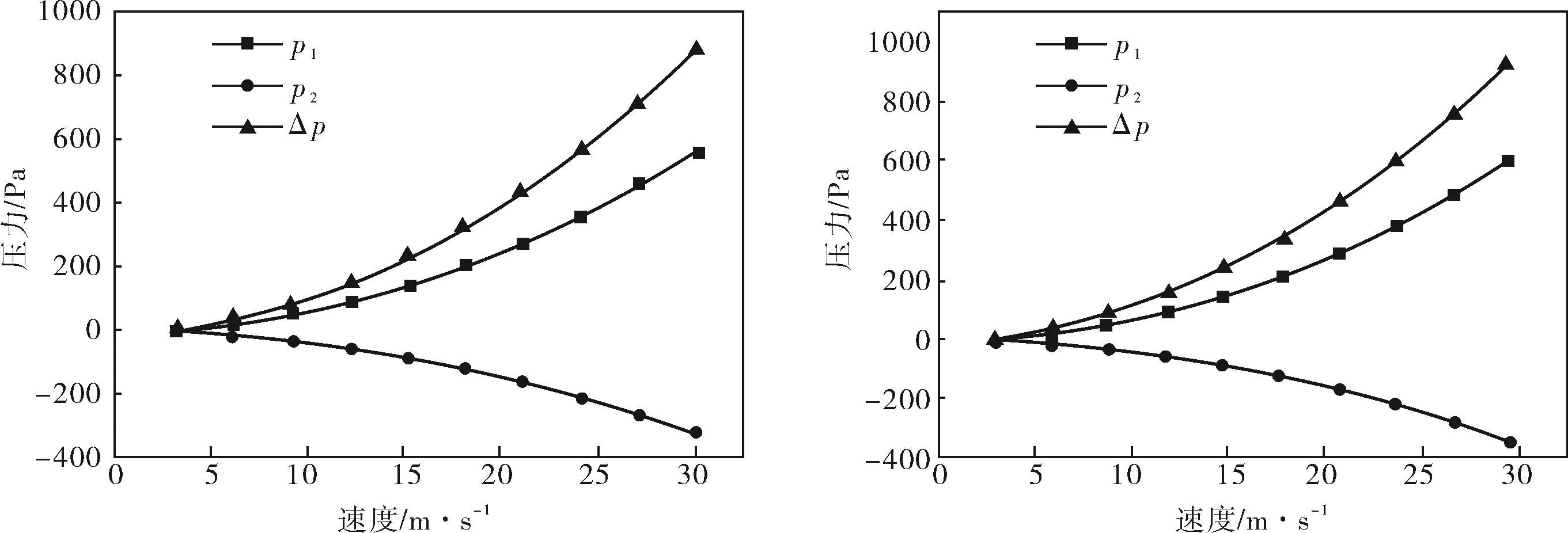
c. D=700mm d. D=800mm
不同管徑管道的測量裝置系數隨速度的變化曲線如圖4所示,圖中的直線表示各組的平均裝置系數,能夠更加直觀地反映各工況下裝置系數偏離平均裝置系數的程度。可以看出,管徑為500mm時裝置系數K的穩定性大不如其他管徑管道的裝置系數,但其穩定性足夠滿足工程應用,穩定性總體上較好,管徑為600mm時管道的測量裝置系數最穩定。

a. D=500mm b. D=600mm
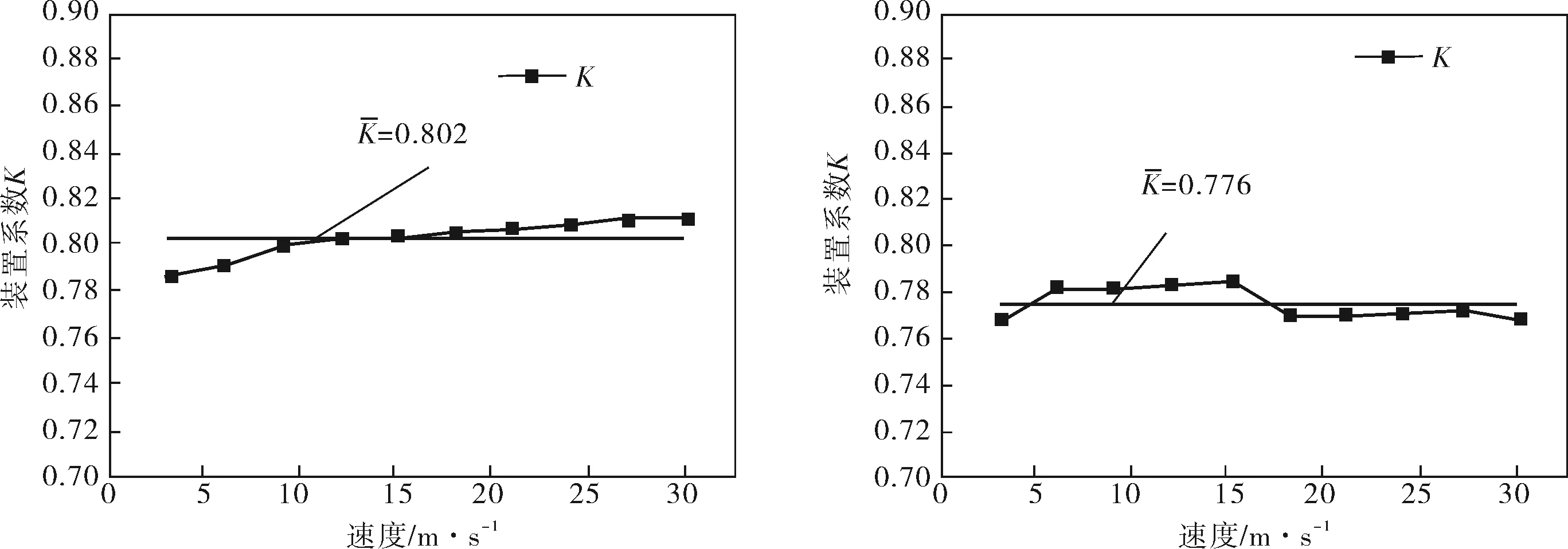
c. D=700mm d. D=800mm
3 結束語
采用Fluent數值模擬軟件對M型流量計進行計算分析,得出不同管道管徑下流量計的性能參數和速度分布,隨著速度的增加,壓差增加,性能更加穩定。仿真結果表明:M型流量計在所計算的幾種工況條件下均有良好的性能,測量裝置系數K線性度較好,其隨管徑的變化有所變化,
但幅度不大,滿足工程應用要求。后續需對管道內不同介質的流動狀態進行數值模擬分析,以使其更具有應用普遍性。
[1] 周云龍,張全厚,劉博,等.基于錐形孔板壓差脈動特性測量濕氣流量[J].化工機械,2013,40(1):22~25.
[2] 葉佳敏,張濤.水平式安裝金屬管浮子流量計的仿真與實驗研究[J].化工自動化及儀表,2005,32(2):67~70.
[3] 徐英,劉正先,張濤.浮子流量計三維湍流流場的數值研究[J].天津大學學報,2004,37(1):74~79.
[4] 王福軍.計算流體動力學分析——CFD軟件原理與應用[M].北京:清華大學出版社,2004:120~131.
[5] 程勇,汪軍,蔡小舒.低雷諾數的孔板計量數值模擬及其應用[J].計量學報,2005,26(1):57~59.

