多場耦合的電磁流量計傳感器感生電勢計算方法

李 波 張 濤 張皎丹

(天津大學電氣與自動化工程學院天津市過程檢測與控制重點實驗室，天津 300072)

電磁流量計是基于法拉第電磁感應定律制成的一種測量管道中導電液體體積流量的儀表，具有與被測液體溫度、粘度及密度等無關，測量范圍大，無壓力損失的優點，被廣泛應用于工業生產。電磁流量計由傳感器與轉換器組成，傳感器負責將管道中的流速信號轉換為電信號，通過電極兩端引入轉換器放大，并轉換成標準電信號輸出。傳感器由磁路系統及電極等組成，磁路系統負責產生工作磁場，電極負責引出電勢，該電勢極其微弱，一般是微伏級，無法直接測量。對于已經確定尺寸的傳感器如何得到它的靈敏度或者已知道傳感器要求的靈敏度如何去設計傳感器的尺寸就成了有待解決的問題。筆者采用有限元數值計算方法，分別從二維和三維角度來計算此問題，并與實驗數據進行對比，有較好的吻合度。三維計算相對于二維計算有更好的計算精度，驗證了筆者所提方法的科學性與合理性。

1 電磁流量計的基本方程①

假設管道中的被測流體是非磁性的，且流體中的位移電流可忽略，不考慮Hall效應及熱電效應等，流體的電導率均勻并滿足Ohm定律。Bevir利用場論中的Green公式推導出了感生電勢的積分形式[1]：

(1)

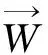
定義J(x,y)如下：

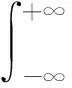
(2)

將式(1)沿直角坐標系分解得[3,4]：

(3)

由于權重函數隨著離開電極所在中心截面距離增大而迅速減小[5]，那些距離電極中心平面較遠的管內空間流體產生的感生電勢對電極間的輸出信號基本上沒有貢獻，因此對于式(3)也可用一個二維的表達式來計算感生電勢，即：

(4)

由于實際中By?Bx，為了計算簡便，式中BxWy項有時也可忽略不計。

2 多物理場的建模仿真

2.1 三維磁場的數值模擬

選取不帶極靴磁軛的馬鞍形線圈傳感器為研究對象，如圖1所示。電磁流量計一般為低頻方波勵磁，在方波勵磁的半個周期內可近似認為通入線圈的為直流電，因此可采用穩態仿真。設定線圈的勵磁電流為與方波信號峰峰值相等的直流電，記為Im。建立仿真模型時[6]，對于不同的口徑，馬鞍形線圈的尺寸會有較大的變化，為了后期能達到對線圈尺寸優化的目的，實現參數化輸入建模仿真，設計了如圖1所示的參數來確定線圈。

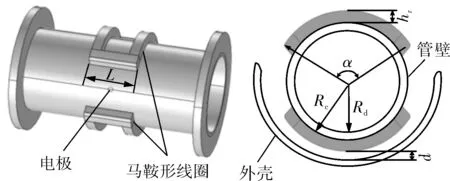
圖1 馬鞍形線圈傳感器及其幾何出參數

建立與實際尺寸完全一致的三維模型，線圈匝數N=800匝，勵磁電流Im=125mA，漆包線直徑Φ=0.38mm。管道橫向和縱向中心截面的磁通密度沿Y軸分布，如圖2所示。

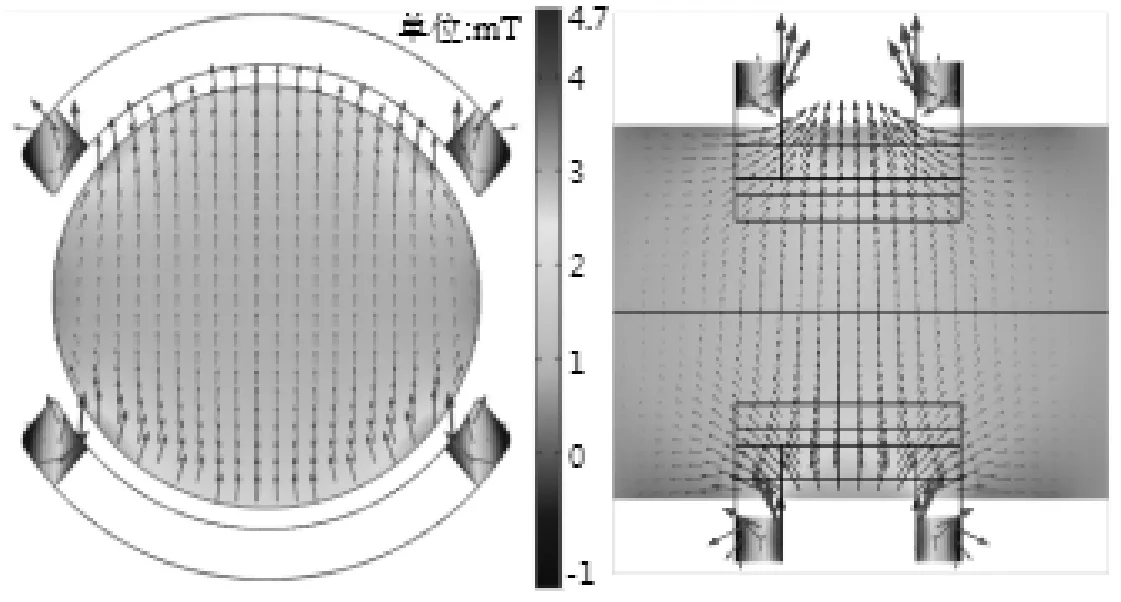
圖2 橫向和縱向中心截面磁通密度沿Y軸分布

2.2 基于“虛電流”定義求解權重函數

點電極下的二維權重函數分布早在上世紀60年代初時Shercliff就給出了數學解析表達式[7]。20世紀70年代，Bevir M K首次引入“虛電流”并將權重函數從二維發展到三維[1]。筆者從“虛電流”的定義出發采用有限元法對二維、三維權重函數建模求解。設定求解域和邊界條件劃分網格并選擇穩態求解器求解，得到點電極下二維權函數分布的數值解，并與Shercliff求得的解析解對比(圖3)。其結果與解析解基本吻合，同樣將此法應用于三維權重函數的求解，其結果如圖4所示。

假設線圈在測量域上產生的磁場均勻，即By=B0，那么無論是采用二維計算還是三維計算，其結果在數值上應該相差不多，即ΔU2d≈ΔU3d，因此再對照式(3)、(4)，不難發現權重函數二維和三維之間的聯系，即：

(5)

2.3 流體速度場分布

實際應用中，一般保證流體在流經電磁流量計時已充分發展，因此可借鑒Nikuradse的1/n冪次律分布來計算管道截面流場的速度分布[2]。湍流與層流的速度分布如圖5所示。

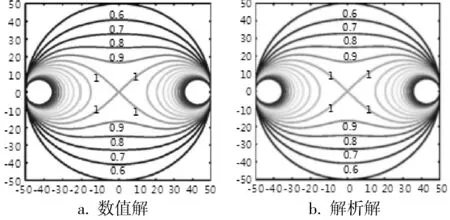
圖3 二維權重函數數值解與解析解對比

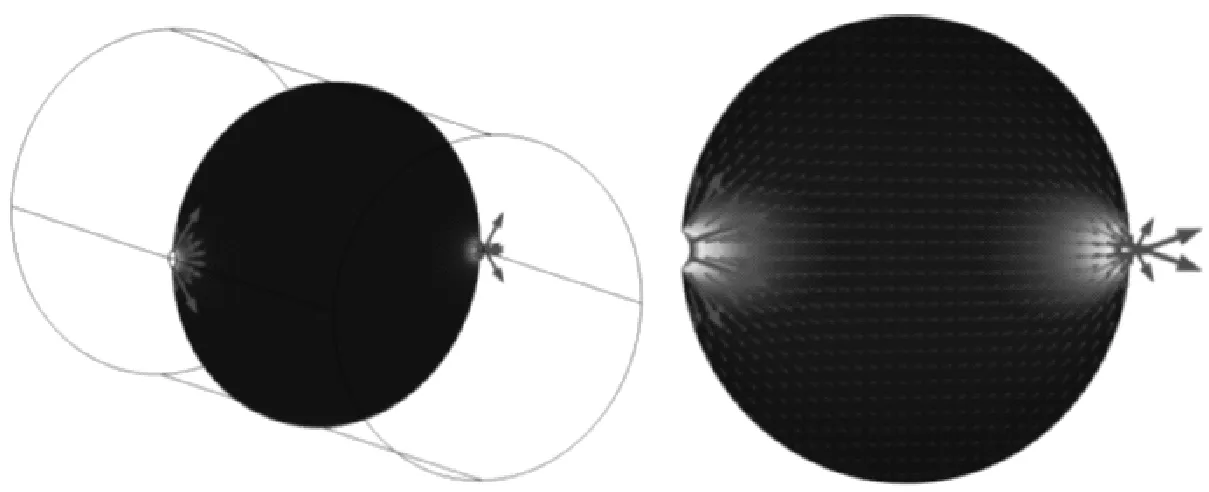
圖4 三維權重函數數值解與解析解對比

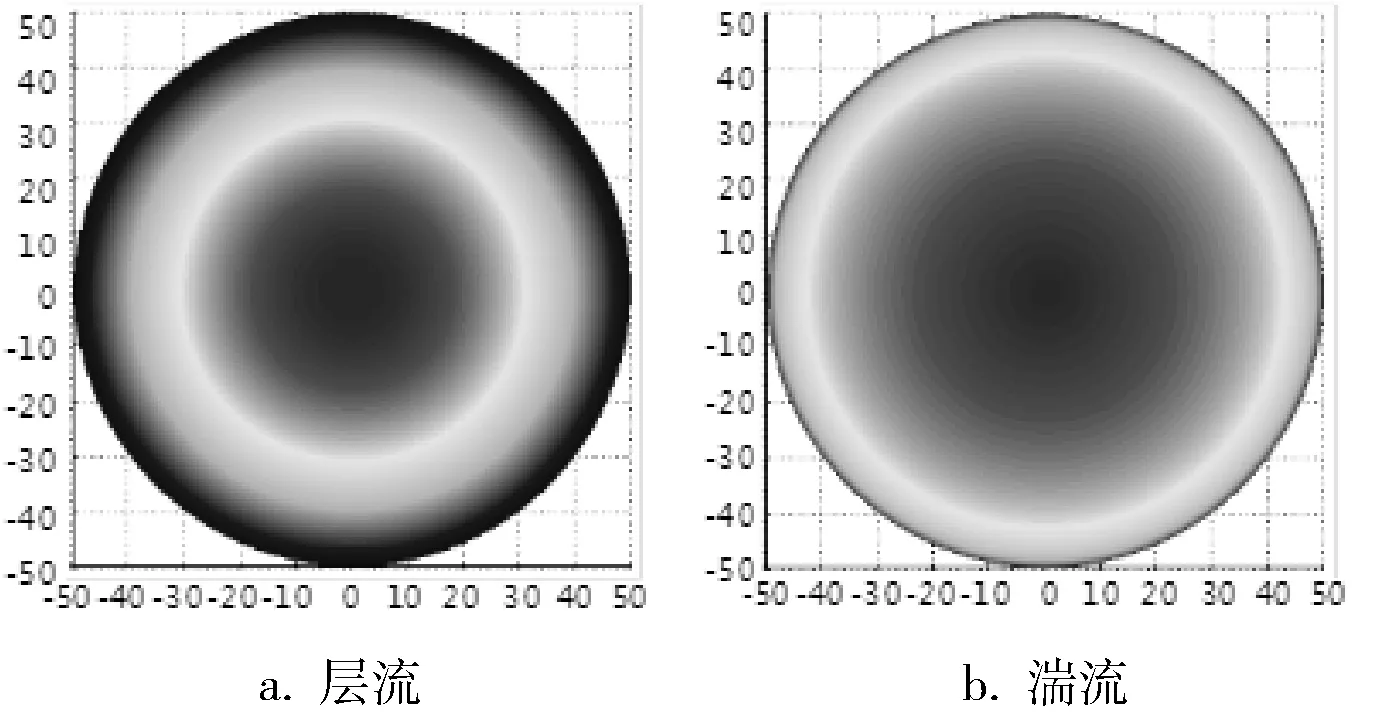
圖5 層流、湍流速度分布

3 多物理場耦合

3.1 二維計算

根據式(4)(電勢的二維計算式)可知，積分區域S即電極所在的中心平面，因此只需要獲得該平面上的磁通密度Bv的分布，采用二維權重函數的計算方法獲得權重函數Wx的分布，并根據公式即可求得該平面上速度Vz的分布情況。在整個中心平面S上，對圓面進行點劃分，每個點代表一個很小的流體微元。點劃分時可確定每一點的坐標(x,y)，前面已獲得了平面S上的Bv、Wx和Vz的分布，通過插值計算可獲得每一點的數值Bv(x,y)、Wx(x,y)和Vz(x,y)，三數相乘然后對整個平面上的各點進行積分即可獲得ΔU2d的數值。

3.2 三維計算

二維計算時忽略了仿真的物理場沿測量管軸向的分布，而這恰恰是三維計算時需要考慮的。在考慮軸向分布時，將測量管沿軸向進行面劃分，為了節省計算資源，在靠近電極的測量管劃分較密而在遠離電極的區域劃分稀疏一點。在劃分的每一個圓面上采用與二維計算時相同的方法確定每個點的物理量，然后代入式(2)中計算出J(x,y)，最后將獲得的J(x,y)代入式(3)即可求得ΔU3d。

3.3 計算方法的優劣

二維計算時只考慮了電極所在的中心平面而忽略其他，是一個面積分問題，難免會計算不精準，但不能否認這能節省大量的計算資源，減少計算時間。三維計算是一個體積分問題，更符合實際情況，對于計算精度也有一定的提高，但計算時間較長。

4 實驗對比

為了驗證仿真計算的準確性和合理性，選取DN100mm口徑的電磁流量計為研究對象，建立與實際尺寸完全相符的幾何模型進行仿真，并在稱重法水流量標準裝置中進行相關的實流實驗。水流量標準裝置管路和實物如圖6所示。該裝置流量穩定性為0.1%，流量范圍為0.005～550m3/h，不確定度為0.005%(k=2)，實驗管道包括50、100、200mm等7種不同口徑。

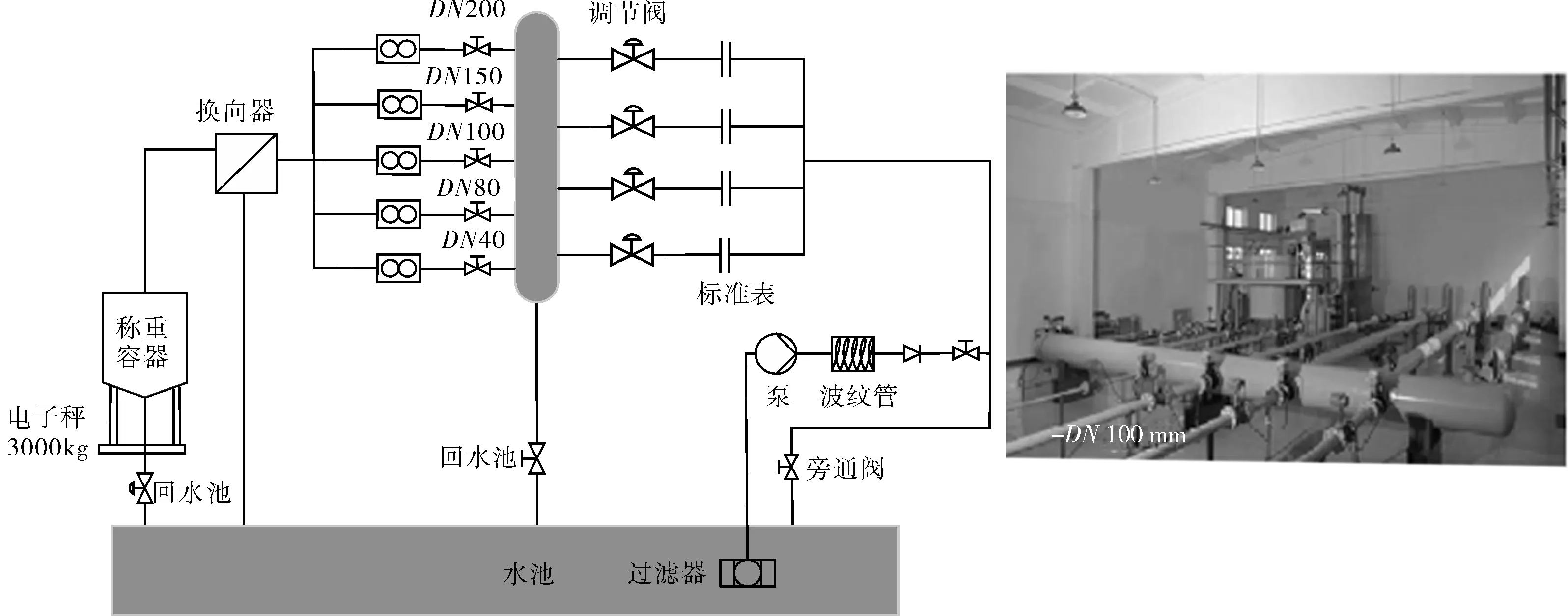
a. 管路圖 b. 實物圖

由于電極兩端能產生的電勢極其微弱，一般設計的靈敏度為μV/(m·s-1)，無法直接測量電極兩端的感生電勢，需要將該信號進行放大才能測量。實驗測量電路的放大倍數記為K。實驗時為方波勵磁，故電極兩端產生的感生電勢經過放大后也為方波，如圖7a所示。測量的流速范圍是0.5～6.0m/s，中間每間隔0.5m/s有一個測量點，每個點測量3次，取3次測量的平均值，記為Ua，即電極兩端感生電勢的實際值。采用前文二維、三維計算方法分別計算電極兩端的電勢，分別記為U2d、U3d。實驗值與仿真值的對比如圖7所示。

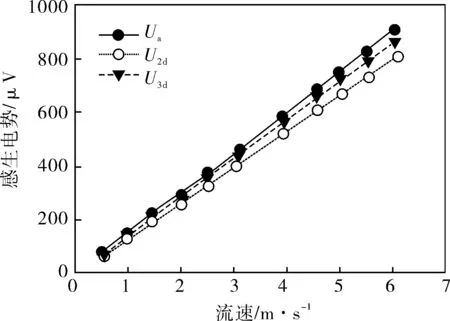
圖7 實驗值與仿真值的對比

從圖7中可以發現，三維計算比二維計算更接近于實際值，三維計算的平均相對偏差為-3.9%，而采用二維計算時平均相對偏差為-11.8%，具體數據見表1。

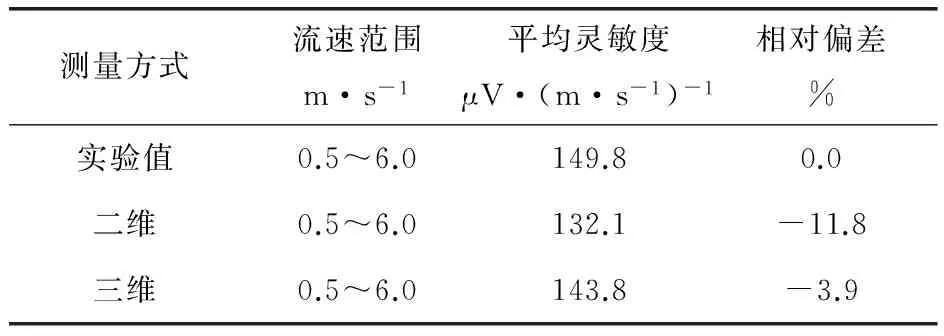
表1 實驗值與仿真值偏差

5 結束語

通過有限元數值計算方法對電磁流量傳感器進行多物理場建模仿真，最終計算出了電極兩端的感生電動勢。分別從二維和三維的角度對傳感器模型進行數值計算，并與實驗值進行對比，發現三維計算比二維計算有著更高的精度，一方面說明了筆者所采用的計算方法的科學性與合理性，另一方面說明了采用三維計算比二維計算有著更高的精度，更能符合實際，但需要耗費較長的時間。

[1] Bevir M K, O′sullivan V T, Wyatt D G. Computation of Electromagnetic Flowmeter Characteristics from Magnetic Field Data[J]. Journal of Physics D: Applied Physics,1981,14(3):373．

[2] 張小章．流動的電磁感應測量理論和方法[M].北京:清華大學出版社，2010．

[3] Michalski A, Starzynski J,Wincenciak S.Optimal Design of the Coils of an Electromagnetic Flow Meter[J].IEEE Transactions on Magnetics,1998,34(5):2563～2566．

[4] Michalski A,Wincenciak S.Method of Optimization of Primary Transducer for Electromagnetic Flowmeter[C].IEEE Instrumentation and Measurement Technology Conference.Brussels,Belgium:IEEE,1996:1350～1353．

[5] 蔡武昌，馬中元．電磁流量計[M].北京:中國石化出版社，2004．

[6] Zimmerman W B J．COMSOL Multi-physics有限元法多物理場建模與分析[M].北京:人民交通出版社,2007:282．

[7] Bevir M K.The Theory of Induced Voltage Electromagnetic Flowmeters[J].Journal of Fluid Mechanics,1970,43(3):577～590.