數學學習應重視讓學生親身體驗

湯海娟

[摘 要]數學知識不是通過教師簡單的講授，也不是通過反復的練習學生就能學會的，只有在課堂上實實在在地去感受才能真正獲得這種有價值的經驗和感受。在課堂上教師要注重學生的學習體驗，讓學生在體驗中感悟數學。

[關鍵詞]感悟 數學 價值

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）35-084

數學課程標準指出：“讓學生在學習活動中體驗和理解數學。”的確，學生只有在課堂上實實在在地去感受才能真正獲得。為此，在課堂上教師要注重學生的學習體驗，讓學生在“悟”中學數學。

一、經歷實踐操作，領悟抽象數學

戰國荀況曾說：“不聞不若聞之，聞之不若見之，見之不若知之，知之不若行之。”因此，在實踐操作的過程中，可讓學生通過自己熟悉的形象思維入手來體驗數學，從形象到抽象，慢慢領悟數學。這樣不僅降低了學習數學的難度，還鍛煉了學生動手操作的能力，發展了學生的手腦協調能力。

例如，比例的應用中有這樣一題：“學校要建一個長80m、寬60m的長方形操場，請畫出操場的平面圖。”教材中要求學生先定比例尺再換算出圖上距離，筆者認為這樣做對于學生來說十分抽象。因此筆者讓學生先動手在紙上畫一個和實際操場長寬比例相同的長方形。有的學生畫長為8cm、寬為6cm的長方形，再求出比例尺1∶1000;而有的畫長為12cm、寬為9cm的，在轉化成比例尺的時候覺得比較麻煩，于是又動手把圖上距離改成好換算的。這樣，學生在實踐操作的過程中領悟了抽象的數學，既保證了比例尺的準確性，又畫出了美觀的圖形。

心理學表明：“學”這一活動最好的方法就是“做”。這種能讓大腦和手真正動起來的學習，不僅能讓每個學生用自己內心的體驗去參與數學學習，感受和理解知識的產生和發展過程，還能在參與過程中學會學習、增強自信。學生通過自身的積極思維與主動參與“做”而獲得的數學知識，才是理解最深刻、掌握最牢固且最有使用價值的知識。

二、經歷合作探究，領悟理性數學

著名人本主義教育家羅杰斯說過：“只有學生自己發現、探究的知識，才是活的、有用的知識。”合作探究這一打破傳統模式的教學方法大多數一線教師都深有體會，但是目前一些形式化的合作探究不僅浪費課堂時間，還制約了學生對理性數學的理解。

例如，“位置與方向”中互換觀測點的問題“上海在北京南偏東30°方向，距離1067千米處;北京在上海北偏西30°方向，距離1067千米處。”筆者問：“這兩句話分別是以什么為觀測點？”“前者是北京，后者是上海。”“它們交換了觀測點，各自所在的位置也不同，這就是位置的相對性。那么互換觀測位置后的關于位置的描述有什么區別和聯系？”通過小組交流，學生很快發現了二者的區別和聯系。“如果交換了觀測點，你們能快速地寫出它們的位置關系嗎？”學生通過合作探究，找到兩地交換后位置的區別與聯系后，再將這個規律運用到實際的問題中去。在這個理論到實際的學習過程中，學生領悟到理性數學的魅力。

三、經歷數形結合，領悟魅力數學

正如華羅庚教授的名言：“數形結合百般好，隔離分家萬事非。”數形結合，是數學中代數與幾何學科的整合和互助，學生在用數形結合的方法解決抽象問題時，能感受到數學學科內代數與幾何之間的聯系，感受數學的魅力，而這種感受和經驗并不是教師說一說，習題做一做就能得到的。

例如，有這樣一道題：“天津到濟南的鐵路長357千米。一列快車從天津開出，同時有一列慢車從濟南開出，兩車相向而行，3小時后相遇。快車平均每小時行79千米，慢車平均每小時行多少千米？”筆者在學生思考之后，引導學生用數形結合的方法解答。如下圖：

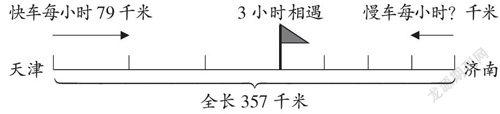
這樣直觀的線段圖不僅可以吸引學生，更重要的是可以幫助學生找到數量關系“快車走的路程+慢車走的路程=總路程”。在這個學習過程中，學生就能感悟到將數量與圖形結合的這種思想的方便之處，充分領悟到數學的魅力所在。

學習心理學表明：“學”這一活動最好的方法就是“做”。這樣不僅能讓每個學生用自己內心的體驗去參與數學學習，感受和理解知識的產生和發展過程，還能在體驗和參與過程中學會學習、增強自信。學生通過自身的積極思維與主動參與“做”而獲得的數學知識，才能是理解最深刻、掌握最牢固且最有使用價值的知識。

總之，新課標指出，人人學有價值的數學;人人都能獲得必需的數學;不同的人在數學上都能得到不同的發展。教師要注重確立學生的主體地位，引導學生經歷學習的全過程，讓學生在經歷中去體驗并得到發展，體驗到學習數學的樂趣，學生通過自己悟到的要比教師講授的體會更深，記憶更牢。

（責編 童 夏）