基于瞬時轉速的電機轉子故障診斷

呂躍剛 張文原 蔡騰潛

(1.華北電力大學控制與計算機工程學院，北京 102206；2.國網冀北電力有限公司秦皇島供電公司，河北 秦皇島 066000)

鼠籠型異步電機廣泛應用于工業生產，但該類電機啟停頻繁、運行時間長、故障多發。轉子斷條是最常見的故障之一，約占全部故障的10%。故障初期電機效率降低，振動增加，嚴重時導條連續斷裂，甚至有可能損壞定子結構，致使電機報廢[1,2]。學者們針對斷條故障提出了多種診斷方法。其中，振動頻譜技術憑借其原理簡單及起步較早等優勢，在國內得到了最為廣泛的應用。然而這種技術硬件成本高、信號干擾大，經濟性和有效性也受到一定的制約。近年來，定子電流分析技術(MCSA)已經引起國內的重視，如方瑞明等利用提取定子電流特定頻率成分的方法診斷轉子故障[3]。然而實際情況下，定子電流信號中被廣泛認可的故障特征頻率(1±2ks)f1成分與基頻成分相距很近，頻率分辨率低及頻譜泄漏等原因導致其極易被湮沒。而在許多以DSP或單片機為硬件核心的在線診斷系統中，數據存儲容量有限，難以通過增長采樣時間的方式提高分辨率。這一特點限制了定子電流分析技術的發展，同時也是一個有待解決的難題。

轉速是電機的重要運行參數，測量技術成熟，成本低廉且準確性高、響應快，目前已被應用于內燃機等旋轉機械故障診斷中[4]。筆者以異步電機瞬時轉速為分析對象，通過對瞬時轉速的時域、頻域分析，尋找其與斷條故障之間的聯系。

筆者依次分析了轉子斷條故障發生后電機內部磁場、轉矩及電流等參量的變化情況，最終得出故障在瞬時轉速中的表現。利用Maxwell軟件對故障電機進行有限元建模，分別對正常狀態下和不同程度故障狀態下的運行過程進行仿真，實驗表明轉速信號中的2sf1成分能良好地反映故障情況，易于識別。此外，轉速波動程度、平均轉速值還能有效反映故障的嚴重程度。與傳統的定子電流分析方法進行對比發現，轉速分析方法簡單易行、準確性高，而且可以降低信號采樣率，有利于有限存儲空間下頻譜分辨率的提高，是一種有實際應用價值的方法。

1 故障模型分析①

傳統定子電流分析方法中，將定子電流頻譜中的(1±2ks)f1頻率成分作為轉子斷條的依據。實際情況中，上述成分極易被基頻成分淹沒，故障提取具有一定的難度。事實上轉子斷條故障會通過磁場作用進一步影響轉速信號，使其在時域、頻域上出現一系列易于識別的故障信息。

1.1 定子電流中(1-2ks)f1成分的產生

假設異步電機定子接入頻率為f1的三相對稱交流電時，轉速為ω。此時轉子中感應出轉差頻率f2=sf1的電流，并產生相對于轉子轉速為ω2=2πf2/p的旋轉磁場。

斷條故障發生后，轉子出現電量不對稱。根據旋轉磁場理論，轉子的不對稱性會使氣隙中產生相對于轉子轉速±2πf2/p的兩個大小相等、方向相反的附加旋轉磁場。其中正向旋轉的磁場在轉速為ω的轉子的承載下，保持與定子電流旋轉磁場同速；而反向附加磁場相對于定子繞組的轉速ωb可由下式計算得到：

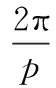
(1)

式中f——轉子轉頻；

f1——電網頻率；

p——電機的極對數；

s——電機轉差率。

可見，當異步電機出現轉子斷條等不對稱故障時，氣隙中會產生相對于定子轉速為ωb的附加旋轉磁場，此磁場會在定子繞組中感應產生頻率fb=(1-2s)f1的感應電流。許多研究將此分量作為定子電流中轉子斷條的故障特征，并通過在定子電流中提取該頻率成分的方式進行故障識別。然而，對于異步電動機，由于轉差率s的值很小(1%～5%),將導致轉子電量不對稱特征頻率(1±2s)f1與50Hz基頻成分相距很近，這樣一來，故障特征成分就極易被幅值強大的基頻成分覆蓋，影響故障識別的準確性。因此傳統的定子電流頻譜分析方法難以滿足故障診斷的要求。

1.2 轉子故障對轉速的影響

故障電機運行過程中，故障信息可以通過氣隙磁場的作用影響轉子轉矩，進而影響瞬時轉速。轉速信號是電機運行過程中的重要參數，其中包含大量電機運行狀態信息，此外，轉速信號可通過光電編碼器等傳感器方便地獲取，信號采集技術成熟，誤差小、響應快，造價低廉。因此，轉速信號適用于對電機進行狀態監測。

假設上述定子電流中故障附加電流分量瞬時表達式為：

ib1(t)=Ib1cos[(1-2s)ω1t-αb1]

(2)

其中，Ib1為此電流分量的幅值，αb1為其初相角。

此電流分量與基波磁通Φ=cos(ω1t-αΦ)作用，使電機電磁轉矩發生波動，頻率為2sf1，則有：

ΔT(t)=3pΦIb1sin[2sω1t-(αΦ-αb1)]

(3)

式中αΦ——定子基波磁通初相角；

Φ——定子基波磁通幅值。

由于轉矩的波動，導致轉速隨之發生相應變化，轉速變化量可由轉矩變化量的積分計算：

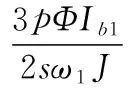
(4)

其中，J為發電機轉子轉動慣量。

可見，轉子斷條故障下，轉速受到轉矩脈動的影響，也出現頻率為2sf1的周期性波動，這表明故障電機瞬時轉速信號中將會包含相同頻率的特征成分。因此對瞬時轉速信號采樣后進行時域及頻域等角度分析，可以提取異步電機轉子斷條的故障信息。此外，穩態下，轉速信號低頻段中僅包含直流成分，頻譜相對簡單，易于故障識別和提取。

實際上，由于轉速出現了頻率為2sf1的周期性波動，靜止的定子繞組中的電流會受到頻率為2sf1的調制，導致其中生成(1±2ks)f1一系列特征頻率成分。

2 有限元故障建模與仿真

眾所周知，在故障狀態下電機三相不對稱，傳統交流電機數學模型不再適用，從數學模型的角度進行故障建模具有極大的難度，而對實體電機進行故障實驗成本高昂，因此對于電機故障研究來說，數據獲取方式始終是一個關鍵難題。Maxwell是一款針對于電磁場仿真的有限元分析軟件，廣泛應用于電機設計等領域，參數設置靈活，適用于故障分析，結果具有一定的可靠性。

圖1所示為鼠籠型異步電機有限元模型，電機極對數為2，額定功率為11kW，額定轉速為1 462r/min，定子36槽，轉子24槽，轉子機械轉動慣量為0.096 82N·m。可以通過減小指定導條的電導率來模擬轉子斷條。

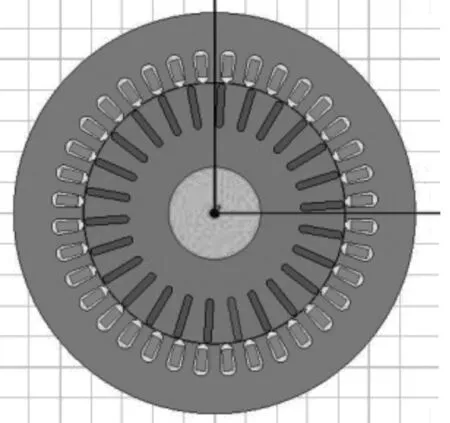
圖1 鼠籠型異步電機有限元模型

令電機在額定負載(80N·m)下運行，采樣率為200Hz。正常狀態下的電機轉速、電磁轉矩、電流信號及其頻譜如圖2所示。可見，正常狀態下，電機轉速和轉矩平穩無周期性波動，電流信號中僅包含50Hz基頻成分。

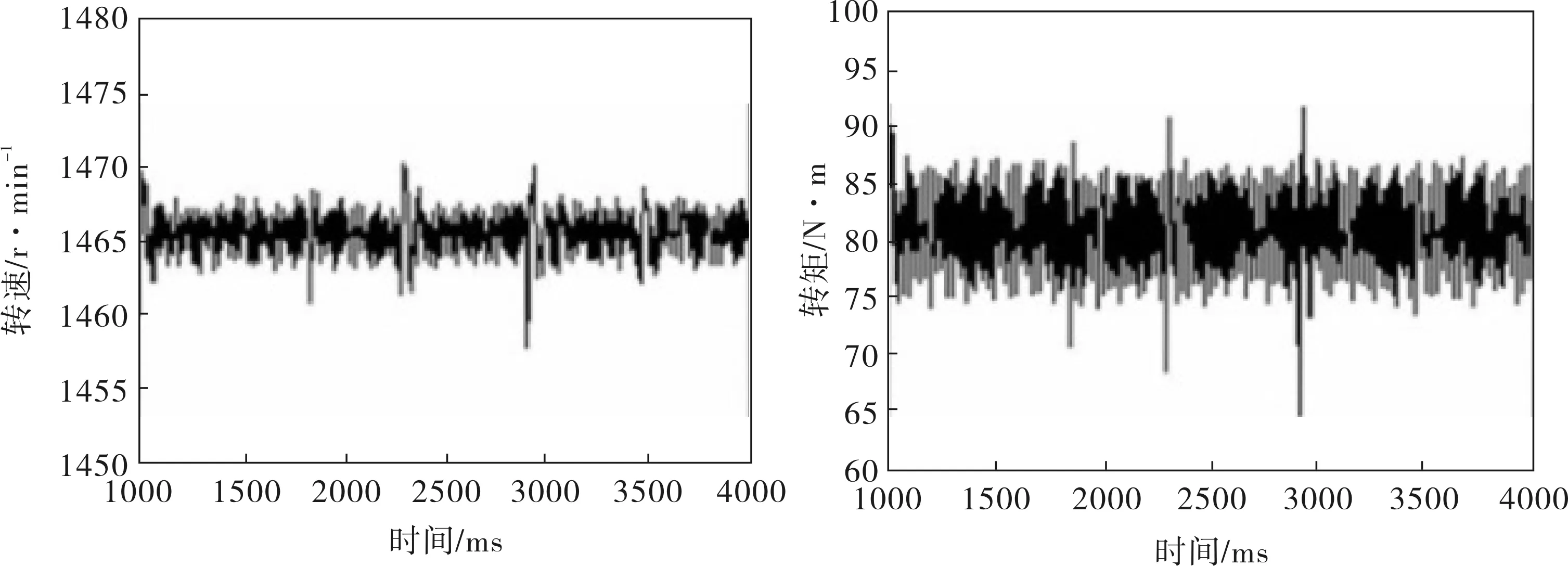
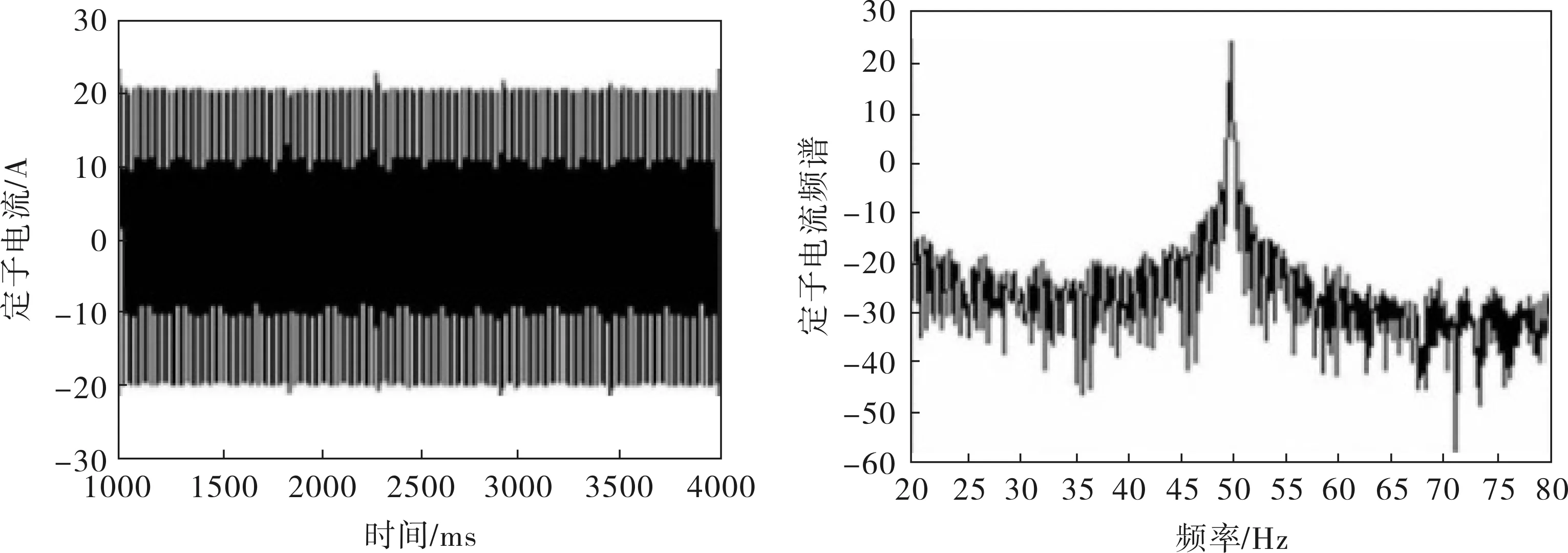
圖2 正常狀態下參數的仿真結果

圖3所示為瞬時轉速信號經去直流運算后FFT頻譜的低頻(0～30Hz)部分，可以看出，轉速信號中僅含直流成分，頻譜成分簡單清晰。

圖3 正常電機瞬時轉速去直流后的FFT頻譜

在相同的運行和采樣條件下，設置電機一根斷條，所得穩態下的仿真結果如圖4所示。由于斷條，轉速出現了周期性變化(s≈0.025，波動周期Tb=1/2sf1≈1/2.5≈0.4s=400ms)。從電流時域波形可見，在轉子故障的影響下，電流波形被調制而出現失真，然而由于頻譜泄漏等原因，其FFT譜上的故障特征頻率(1±2ks)f1成分并不明顯，只有在(1+4s)f1≈55Hz處出現了尖峰，與故障相對應，但與基頻相比，故障特征頻率幅值極小，難以分辨。

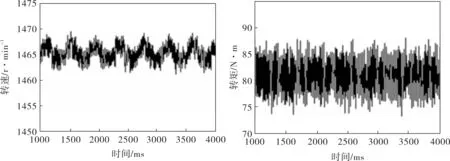
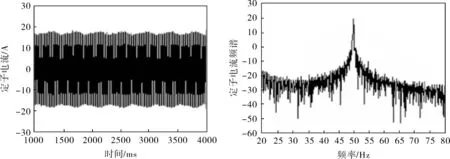
圖4 電機一根斷條時額定負載下仿真結果

將瞬時轉速信號經過去直流后，做FFT運算，得到如圖5所示的頻譜低頻部分，可清晰地看見包含的2sf1=2.5Hz成分及其倍頻4sf1=5Hz，證明轉速在以此頻率進行周期性波動。

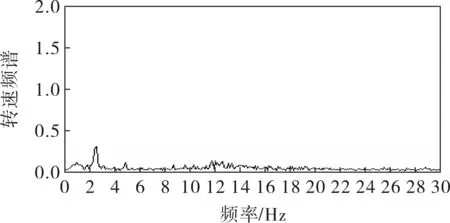
圖5 電機一根斷條時額定負載下轉速的FFT頻譜

值得一提的是，轉速信號中頻率成分簡單，特征頻率附近無干擾成分，非常易于故障的識別。此外，由于異步電動機轉差率很小(1%～5%)，故轉速中故障特征頻率一般小于5Hz，所以，在工程應用中，存儲空間有限時，可以大幅減小轉速信號的采樣率，進而延長采樣時間，將頻譜分辨率提高幾十倍，提高故障分辨的準確性。

3 故障程度對故障特征的影響

事實上，故障后由于相鄰導條電流及所受電磁力增大，通常故障會進一步發展為連續斷條的情況。現通過實驗，分析斷條根數對瞬時轉速等參數的影響程度。

在相同的運行和采樣條件下，為電機配置了1～3根連續斷條。不同故障程度下定子電流和瞬時轉速的頻譜對比如圖6所示。可以看出，隨著故障程度的增加，定子電流中的特征頻率成分幅值增大(如(1-2s)f1成分幅值由-6上升至2)，且諧波成分也趨于明顯。轉速的頻譜中，2sf1成分幅值同樣隨著斷條根數的增加而變大，且變化更為明顯(由0.4增大至8.0)。在轉子為3根斷條的情況下，由于故障嚴重導致轉速波動較大，導致0～1Hz低頻成分幅值增大，但2sf1成分仍可輕易分辨。

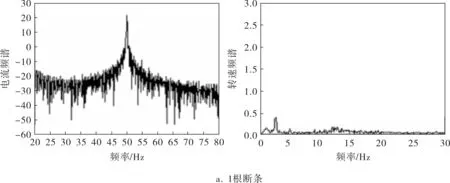
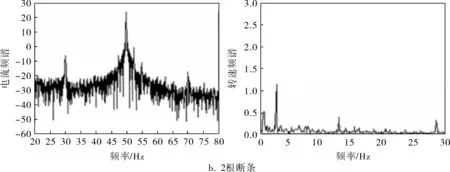
圖6 不同故障程度下定子電流和瞬時轉速頻譜對比

轉速原始信號高頻噪聲較大，而本方法關注的頻率范圍是5Hz以下的低頻帶，將3種情況下的轉速信號進行低通濾波后，所得曲線如圖7所示。可見，轉速的波動幅度隨著斷條根數的增加而增大，且穩態轉速的大小有著隨斷條根數的增加而下降的趨勢。

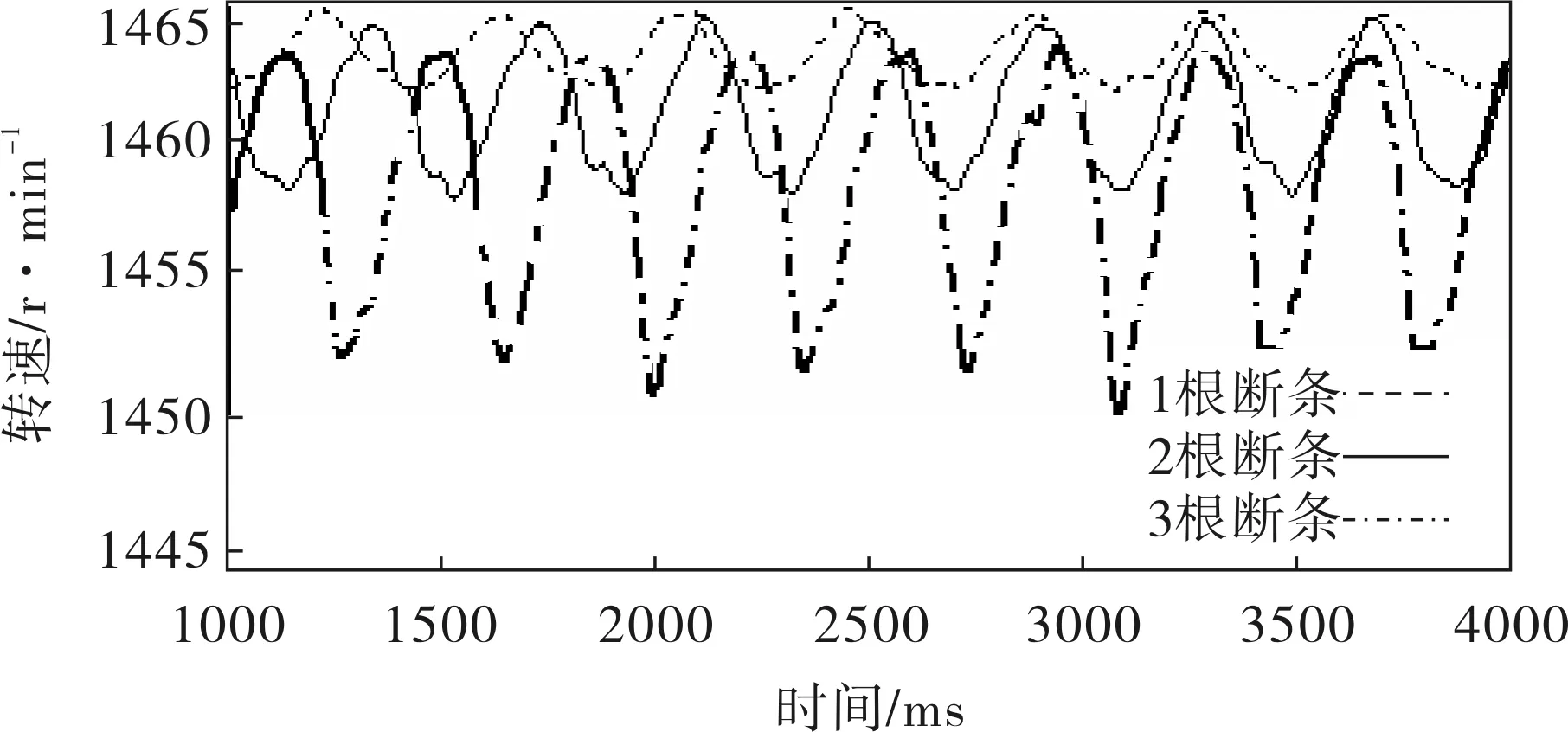
圖7 不同故障程度下的瞬時轉速

表1統計了3種故障狀態下由電機轉速信號計算而得的統計量，可見，隨著斷條根數的增加，電機穩態時的平均轉速有所下降，而電磁轉矩卻未發生變化，這種現象的主要原因為：斷條故障導致轉矩和轉速信號波動的增加，消耗了部分定子輸入的能量，導致轉速的下降。

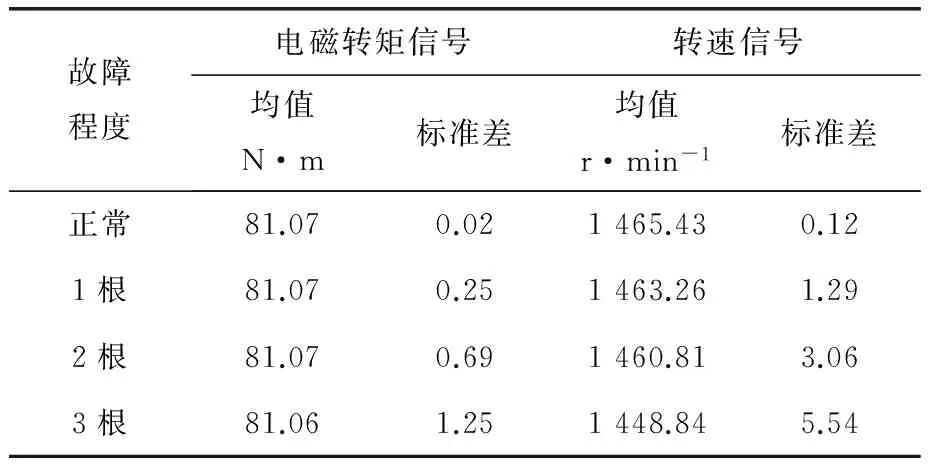
表1 不同故障程度下轉速和轉矩數據統計

4 結束語

筆者提出了一種基于轉速分析的異步電機轉子斷條診斷方法，通過利用Maxwell有限元分析軟件進行故障建模并仿真，從時域、頻域多個角度分析了轉速信號中的故障信息。實驗結果表明：瞬時轉速中2sf1成分能夠有效反映故障情況，頻率成分明顯，清晰易辨。此外，瞬時轉速波動程度、平均轉速值均受連續斷條根數的影響，可作為判斷故障嚴重程度的依據。與傳統的定子電流分析方法進行對比發現，轉速分析方法簡單易行、準確性高。特別地，這種方法降低了對信號采樣率的要求，有利于有限存儲空間下頻譜分辨率的提高，是一種有實際應用價值的方法。

[1] 宋軍艦，郝點，曹建強.高速轉子故障模擬實驗研究[J].化工機械，2011,38(4):417～419.

[2] 常穎，李聰，張風波.離心機轉子力學性能的有限元分析及測試[J].化工機械，2012,39(4):478～481,502.

[3] 方瑞明，鄭力新，馬宏忠，等.基于MCSA和SVM的異步電機轉子故障診斷[J].儀器儀表學報，2004，24(5)：115～119.

[4] 王維琨，江志農，張進杰.基于神經網絡和瞬時轉速的發動機失火故障研究[J].機電工程，2013，30(7)：824～827.