電動帆航天器谷神星探測任務軌跡優化

霍明英，彭福軍，趙 鈞，謝少彪，3，齊乃明

(1．哈爾濱工業大學航天學院，哈爾濱150006;2．上海宇航系統工程研究所，上海201108;3．上海航天技術研究院，上海201109)

0 引言

谷神星(Ceres)是太陽系內的一顆矮行星，同時也是位于小行星帶內最大的天體。目前，谷神星被很多學者認為是尚存的原行星(萌芽期的行星)之一，于45．7億年前在小行星帶中形成［1］。雖然太陽系內大多數的原行星不是和其他的原行星合并成為類地行星，就是被木星彈射到太陽系外，但是谷神星被認為是留存下來較為完整的一顆原行星［2］。因此，對谷神星的探測將非常有助于了解太陽系的起源。不僅如此，歐洲航天局已于2014年1月確認谷神星上有水蒸氣冒出。谷神星的紅外線光譜也顯示水合礦物非常廣泛的存在于谷神星上，這都證明在其內部可能存在著大量的水。甚至有天體生物學方面的科學家認為谷神星有可能是潛在的宜居性星球，因為其表面存在著生命需要的三個基本條件:液態水、能量來源和某些化學成分［3］。因此，對谷神星的探測不僅能夠對太陽系形成理論提供佐證，也可以對其地表是否存在水甚至是原始生命一探究竟。鑒于谷神星探測具有很大的科學意義和現實意義，美國航空航天局(NASA)于2007年9月發射了“黎明”號太空飛船，于2011年7月抵達灶神星(Vesta)，2015年3月抵達谷神星［4］。為了將來能更快更廉價地對谷神星進行探測甚至取樣返回，本文提出將電動太陽風帆(簡稱電動帆)推進技術應用于谷神星的探測任務中。

電動帆是由芬蘭航天專家Janhunen于2004年在磁帆［5］的基礎上提出的一種新興的無推進劑消耗的推進方式［6］。與更為人熟知的太陽帆相同，電動帆可以在不消耗任何推進劑的情況下產生連續的推力，因此非常適用于長期的空間探測任務;與太陽帆不同的是，電動帆的動力來源為太陽風中帶電粒子的動能沖力，而不是太陽光壓。電動帆原理示意圖如圖1所示，電動帆由許多根長而細的金屬鏈所組成，這些金屬鏈通過航天器自旋進行初始展開和形狀保持。航天器上的太陽能電子槍通過向外噴射電子使金屬鏈始終保持在高度的正電位。這些帶電金屬鏈會排斥太陽風中的正電粒子，從而最終利用太陽風的動能沖力為航天器產生連續的推力，并使航天器在飛行過程中不消耗任何推進劑。Janhunen對電動帆的推進效率與目前常規推進技術進行了對比分析。分析結果表明由于電動帆在工作過程中不損耗任何推進劑，因此能夠為飛行器提供持續不斷的推力，工作壽命很長。通過理論計算表明，在為期10年的任務中，同樣質量的電動帆所能產生的速度增量是同樣質量化學火箭發動機所能產生增量的1000倍左右，同樣質量電火箭發動機(SEP)所能產生增量的100倍左右［7］。同太陽帆對比方面，由于太陽帆產生的推力與相對太陽距離平方成反比關系，而電動帆產生的推力與相對太陽距離一次方成反比［8］。因此，在星際遠航任務中，電動帆的推力衰減速度相對于太陽帆的推力衰減速度較慢。而且由于電動帆利用正電場對太陽風質子流進行反射，減少了反射材料質量。在同等特征加速度要求下，電動帆比太陽帆質量更輕;在同等載荷比例的情況下，電動帆產生的加速度更大。

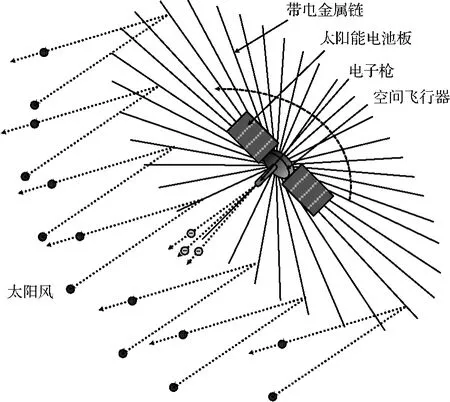
圖1 電動帆原理示意圖Fig．1 Conceptual sketch of an electric sail

鑒于電動帆在深空探測中的巨大潛力，歐盟于2010年12月組織召開了電動帆項目(項目編號:ESAIL EU FP7)啟動會議，資助“電動帆推進技術研究項目”170萬歐元資金。在“歐洲第七框架計劃”的資助下，歐洲各國相關學者對電動帆開展了一系列理論及實驗研究。Mengali和Quarta基于火星探測任務為背景采用間接優化算法對電動帆和太陽帆的運動軌跡進行了優化，并對比了電動帆與太陽帆的性能。通過對比可以看出，太陽帆產生的推力與相對太陽距離平方成反比關系，而電動帆產生的推力與相對太陽距離7/6次方成反比(Janhunen已通過實驗更正為電動帆產生的推力與相對太陽距離一次方成反比［8］)。因此，在星際遠航任務中，電動帆的推力衰減速度相對于太陽帆的推力衰減速度較慢［9］。他們還將電動帆應用于太陽系外探測任務，并通過間接優化算法對不同特征加速度電動帆的太陽系外探測軌跡進行了優化設計。軌跡優化結果表明，一個中等性能的電動帆完成太陽系外探測所用的時間為15年［10］，是旅行者1號的1/3左右。他們基于間接優化方法還對電動帆的各種空間飛行任務進行了軌跡優化，結果均表明電動帆在深空探測領域方面有很大的潛力［11－13］。

本文作者在前期的研究工作中，采用高斯偽譜法對電動帆自地球至火星的二維軌跡優化問題進行了研究［14］。在研究中忽略了火星軌道面與地球軌道面之間的傾角以及星歷約束，將實際的三維軌跡優化問題簡化為二維軌跡優化問題。由于谷神星公轉軌道的軌道傾角較大(10．585°)，所以這種簡化假設將不適用于谷神星探測任務分析中。本文在考慮星歷約束的情況下，對電動帆自地球至谷神星的三維軌跡優化問題開展研究。并提出一種基于高斯偽譜法和遺傳算法的混合優化算法，這種優化算法采用遺傳算法生成高斯偽譜法中所需的狀態變量及控制變量初值，既避免了單純高斯偽譜法初值猜測繁瑣的問題，也克服了Mengali和Quarta所采用的間接優化算法對協態變量初值敏感的問題。基于此優化算法，在不同特征推力加速度和發射時間的情況下，對電動帆航天器自地球至谷神星的過渡軌跡進行了優化，并分析了上述因素對飛行任務的影響。

1 轉移軌跡優化問題描述

由于太陽風粒子流在行星引力球內受到行星磁場的影響而變得較為復雜，所以本文中電動帆軌跡優化問題主要集中于以太陽為引力中心的二體問題。為了提高數值計算效率，引入參考距離和參考時間對整個軌跡優化問題進行無量綱化處理。參考距離為一個天文單位(1au)，參考時間為地球相對太陽的公轉周期。

圖2 參考坐標系及推進加速度特征角Fig．2 Reference frames and propulsive acceleration's characteristic angles

1．1優化性能指標

傳統航天器軌跡優化問題的性能指標大致可以分成三種，即燃料最優、時間最優和時間燃料混合最優。由于電動帆航天器在飛行過程中利用太陽風中帶電粒子的動能產生推力而不消耗任何推進劑，因此電動帆航天器軌跡優化問題中的優化性能指標通常選為時間最優［9－10］，優化性能指標如下:

其中，t0為任務初始時刻，tf為任務終端時刻。在電動帆軌跡優化問題中，終端時刻tf通常為一個未知變量，而初始時刻t0可以是一個已知變量，也可以當做一個未知變量來處理。當初始時刻t0為未知變量時，軌跡優化問題不僅要得出最優的過渡軌跡，還要得出使性能指標最優的任務開始時間。

1．2動力學微分約束

在描述電動帆動力學方程時主要涉及到兩個參考系，即日心黃道參考系T⊙(x，y，z)和軌道參考系TO(xo，yo，zo)。如圖2所示，日心黃道參考系的原點為太陽中心，正x軸指向歷元J2000．0時刻平春分點方向，正z軸垂直于J2000．0時刻黃道面并指向黃道北極方向，y軸與x軸和z軸構成右手系。軌道參考系的原點位于電動帆航天器質心，正zo軸為太陽－電動帆航天器的矢量方向，yo軸與zo軸和日心黃道參考系中的z軸垂直，方向指向飛行運動方向，xo軸與yo軸和zo軸構成右手系。電動帆航天器在日心黃道參考系下的動力學方程為:

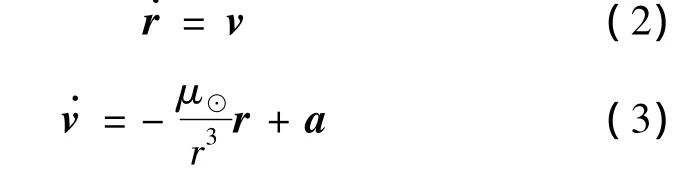
式中:μ⊙為太陽的引力常數;r=［rx，ry，rz］T為航天器在日心黃道參考系下描述的位置矢量;r=r為航天器與太陽的相對距離;v=［vx，vy，vz］T為航天器在日心黃道參考系下描述的速度矢量;a為電動帆的推進加速度矢量。

電動帆的推力是由太陽風粒子的速度、密度以及帶電金屬鏈的電壓、長度和根數所決定。當電動帆遠離(接近)太陽時，所能利用的太陽風粒子速度和密度將減小(增大)，Janhunen通過理論推導及實驗發現電動帆產生的推力與相對太陽距離一次方成反比［8］。另外，當電動帆金屬鏈長度和根數一定時，電動帆可以通過太陽能電子槍向外噴射電子調整金屬鏈的電壓，進而實現對推力的調整。參考Janhunen通過實驗獲得的電動帆推力模型［8，15］以及圖2，電動帆推力加速度矢量在日心黃道參考系下可以寫作:

式中:a⊕為電動帆的特征加速度，即電動帆距離太陽r⊕=1au處所能產生的最大加速度值;κ∈［0，1］為電動帆推力開關系數，可以通過電子槍調整金屬鏈的電壓來調整電動帆整體的推力，這一特性與太陽帆有很大的不同;當κ=0時，電子槍處于關閉狀態，電動帆無推力輸出;當κ=1時，電動帆以最大特征加速度進行工作;α∈［0，αmax］為推進錐角，即電動帆推進加速度矢量與zo軸之間的夾角，Janhunen通過實驗表明，電動帆航天器的推進錐角不能超過一個安全穩定閾值αmax，否則會造成電動帆航天器構型的不穩定;β∈［－π，π］為推進鐘角，即電動帆推進加速度矢量在xoyo平面投影分量與xo軸之間的夾角，逆時針為正;θ∈［0，π］和φ∈［－π，π］為電動帆的極角和方位角，與電動帆位置矢量在日心黃道系下坐標［r］T⊙?［rx，ry，rz］T的關系為

將式(3)和式(4)代入式(1)和式(2)，便可獲得電動帆航天器的動力學方程:

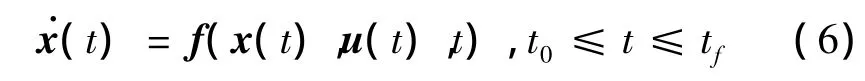
式中:狀態變量為電動帆的位置及速度，即x?［rx，ry，rz，vx，vy，vz］T;控制變量為影響電動帆推進加速度矢量的兩個推進角α，β和推力開關系數κ，即u?［α，β，κ］T;狀態微分函數f(x(t)，u(t)，t)簡記為［f1，f2，f3，f4，f5，f6］T。

1．3邊界約束

電動帆航天器軌跡優化問題中的邊界條件約束主要包括初始狀態約束和終端狀態約束。假設電動帆航天器在初始時刻位于地球逃逸拋物線軌跡上，且逃逸剩余能量為零，初始狀態約束可寫作:

其中rx⊕(t0)，ry⊕(t0)，rz⊕(t0)和vx⊕(t0)，vy⊕(t0)，vz⊕(t0)為地球t0時刻在日心黃道參考系下的位置和速度，可通過美國噴氣推進實驗室(JPL)發布的DE405星歷計算得出［16］。

為了完成電動帆自地球至谷神星的過渡，須在終點時刻tf時的狀態變量與谷神星狀態變量一致，所以終端約束條件可寫作:

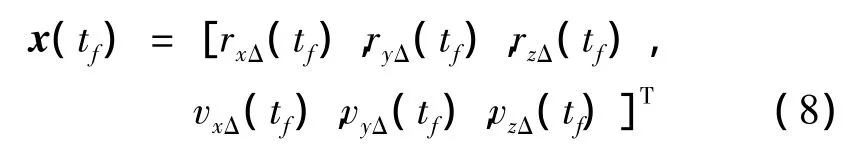
式 中:rxΔ(tf)，ryΔ(tf)，rzΔ(tf)和vxΔ(tf)，vyΔ(tf)，vzΔ(tf)為谷神星tf時刻在日心黃道參考系下的位置和速度，可通過谷神星的軌道根數計算得出。

1．4路徑約束

由于航天器距離太陽越近，電動帆帶電金屬鏈所接觸到太陽風高能粒子的溫度、速度和密度都會變得越大，電動帆的使用壽命會越短，所以為了保證電動帆中的金屬鏈能夠長期穩定地工作，要求電動帆在飛行過程中相對太陽的距離應大于電動帆航天器允許的最小距離rmin。若電動帆金屬鏈材質為鋁合金，一般假設rmin=0．5au。綜上所述，電動帆航天器在飛行過程中的路徑約束可寫作:

2 基于高斯偽譜法和遺傳算法的軌跡優化策略

針對單純高斯偽譜法［17］初值賦值繁瑣的問題，本文提出一種結合高斯偽譜法和遺傳算法的混合優化方法。混合優化算法的優化策略如下:首先以較少離散點進行高斯偽譜法離散化，并通過罰函數將有約束優化問題轉化成無約束優化問題，應用遺傳算法對此優化問題進行全局尋優，并對遺傳算法獲得的結果進行三次樣條插值;然后以較多離散點進行高斯偽譜法離散化，并以可行解插值結果作為最優解計算的初值，最后采用序列二次規劃算法在此初值基礎上計算得出最優解，基于混合優化算法的電動帆軌跡優化流程圖如圖3所示。

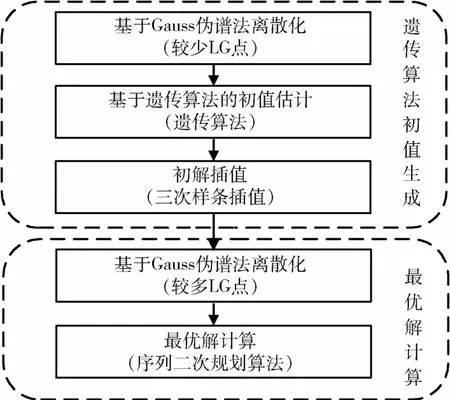
圖3 混合優化算法計算流程Fig．3 The flow chart of the hybrid optimization method

2．1基于高斯偽譜法離散化

最優控制問題的時間區間為［t0，tf］，而高斯偽譜法的離散點分布在區間［－1，1］之間［18］。所以需要通過引入一個新的時間變量τ，將上述定義在［t0，tf］區間上的最優控制問題轉化成定義在［－1，1］區間內，時間變換關系為:

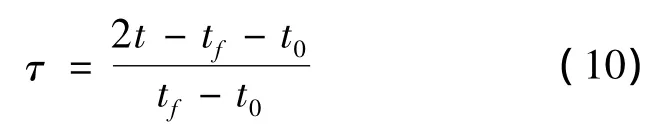
由于電動帆航天器軌跡優化問題中的性能指標函數不包含積分項，所以在離散化后的非線性規劃問題中仍可以寫成非常簡單的形式:

為了將原無限維的連續非線性最優控制問題轉化成有限維的非線性規劃問題，需要用N階Lagrange插值多項式對原問題中連續的狀態變量和控制變量進行插值:

式中:X(τ)和U(τ)分別為狀態變量和控制變量的N階近似多項式;Lk(τ)，k=1，2，…，N，為N階Lagrange插值多項式:

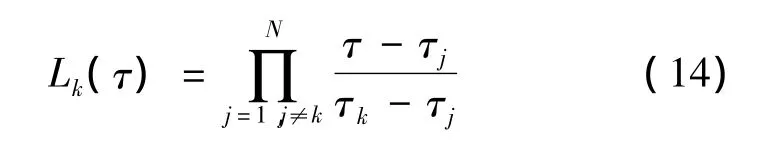
式中:τk，k=1，2，…，N為N個Legendre-Gauss(LG)點，狀態變量和控制變量是在這些非均勻分布的LG點上進行離散化的。這N個LG點是N次Legendre多項式的零點，N次Legendre多項式的表達式如下:

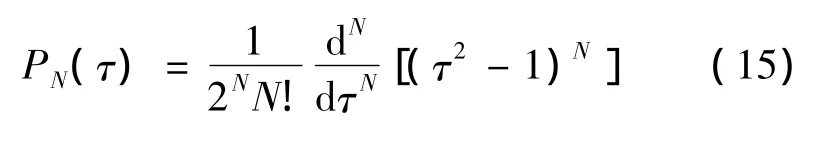
但是這些離散點未包括初始時刻及終端時刻所對應的點，所以定義τ0=－1和τN+1=1分別對應初始時刻和終端時刻。為了表達的方便，簡記狀態變量在離散點 τi，i=0，．．．，N+1上的值X(τi)為Xi，控制變量在離散點 τi，i=0，…，N+1上的值U(τi)為Ui，時間在離散點 τi，i=0，…，N+1上的值t(τi)為ti。

為了將連續的非線性最優控制問題轉化成非線性規劃問題，需要把狀態變量的微分約束轉化成等式約束。對式(11)求導可得:

式中:Dk，i，i=0，1，…，N，k=1，2，…，N是狀態微分矩陣D中的一個元素，可通過下式進行計算:

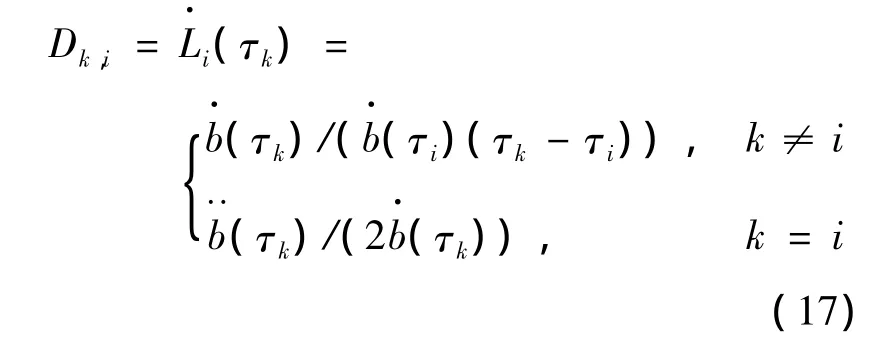
至此，便可將式(5)中描述的6個狀態變量微分約束轉化成下面所示的6N代數等式約束:

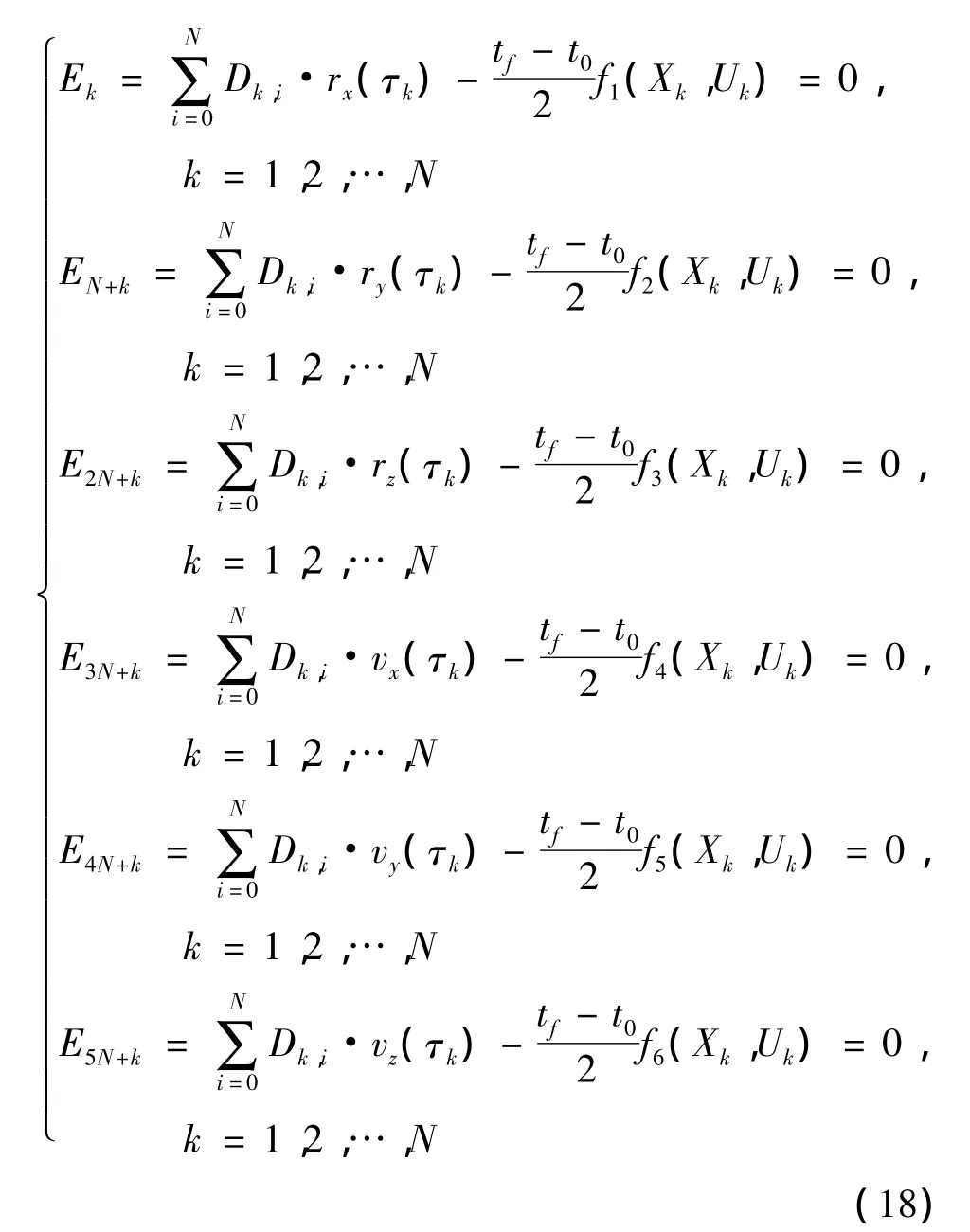
通過高斯積分可獲得電動帆航天器在終點時刻tf的狀態，進而將式(7)描述的邊界條件約束轉化為6個等式約束:

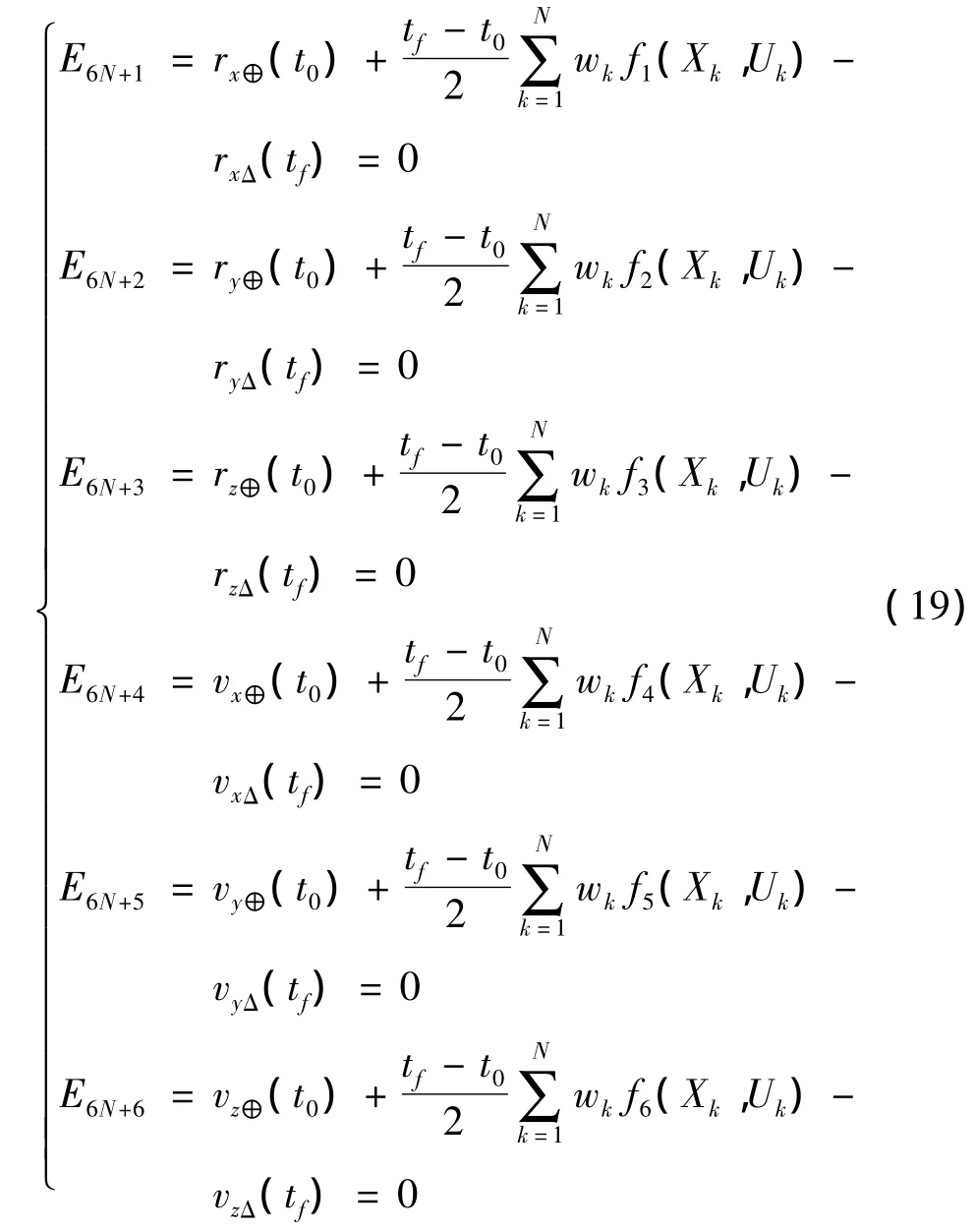
式中:wk，k=1，2，…，N，為高斯積分中的積分權重。

將路徑約束式(8)在LG點上進行離散化，便可得到離散化的路徑約束:

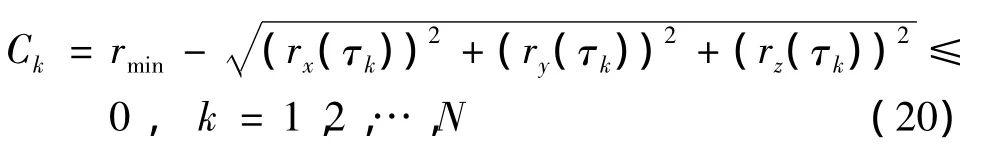
綜合式(10)和式(17)～(19)，便可將式(5)～(8)描述的連續最優控制問題轉化成下述的非線性規劃問題:

對于初始時間t0不固定的電動帆航天器軌跡優化問題，通過高斯偽譜法離散化所得到的非線性規劃問題中共有9N+2個設計變量，分別是6N個狀態變量，3N個控制變量，以及初始時間t0和終端時間tf。等式約束個數為6N+6個，不等式約束個數為N個。

2．2基于遺傳算法的初值生成

對于式(20)所描述的非線性規劃問題，序列二次規劃算法是最常用的參數化尋優方法，但是在實際應用中卻存在一定困難。當選取LG點個數N較多時，設計變量數目會比較龐大，為序列二次規劃算法給定設計變量初值會十分繁瑣，且在無先驗知識情況下有一定難度。假設LG點個數N=60，根據上一節討論的內容可知設計變量個數為542。對于如此多的設計變量，在序列二次規劃算法應用中給定設計變量初值的工作會比較繁瑣，且不恰當的初值會使問題收斂到不可行解。不僅如此，序列二次規劃算法不具備全局尋優的能力，所得到的解主要決定于所猜測的設計變量初值，所以多是靠近初值最近的局部最優解。

因此，本文提出采用遺傳算法全局尋優獲得高斯偽譜法中非線性規劃問題狀態變量及控制變量的初值。通常來說遺傳算法只能用于處理無約束的參數優化問題，然而本節中的非線性規劃問題是有等式約束及不等式約束的。因此，優化問題的目標函數將不只包括時間最優問題，也應該通過增加罰函數將等式約束考慮在內。基于遺傳算法優化問題的性能指標函數(適應度函數)可寫成:

式中:M為懲罰系數。

2．3基于序列二次規劃的最優解計算

序列二次規劃算法是目前應用最廣泛且適用性最好的一種基于梯度的非線性規劃問題求解方法。序列二次規劃法的優點是計算效率高、收斂速度快且所得解精度較高，缺點是需要提供初值猜測，且所得的解對設計變量初值猜測具有一定依賴性，非常容易得到局部最優解。因此，本文通過遺傳算法在無任何初值猜測的情況下通過全局搜索生成較少LG離散點的初解，然后通過插值得到序列二次規劃算法所需的初值猜測。這樣就實現了在無任何初始輸入的情況下，完成對電動帆航天器軌跡優化問題最優解的求解。避免了在無先驗知識的情況下，對初值進行猜測十分繁瑣且困難的情況。而且由于所使用的設計變量初值是通過全局搜索而生成的，所以所獲得的解更接近于全局最優解。本文中序列二次規劃算法所要處理的非線性規劃問題如式(15)所示，這類非線性規劃問題可通過非線性規劃求解器SNOPT［19－20］進行求解。

3 計算結果分析

3．1仿真算例

本節在電動帆航天器自地球至谷神星轉移軌跡優化中，假設電動帆航天器在初始時刻位于地球逃逸拋物線軌跡上，且逃逸剩余能量C3=0 km2/s2。谷神星的位置和速度通過軌道根數(如表1所示)計算得出，計算中忽略了谷神星軌道的章動影響。電動帆航天器的特征加速度為a⊕=1 mm/s2，最大推進錐角αmax=35°，最小允許相對太陽距離rmin=0．5au。飛行初始時刻的選擇范圍為2020年1月1日(JD2458849．5)到2030年12月31日(JD2462866．5)。在基于遺傳算法的初值計算中，LG離散點個數為10，種群大小為200，迭代次數為50，懲罰系數為100。在基于序列二次規劃算法的最優解計算中，LG離散點個數為60，約束允許誤差為10－7。

基于上述參數對電動帆航天器自地球－谷神星飛行軌跡進行了優化，數學仿真運行的環境為MATLAB(R2010a)，運行平臺為雙核2．7GHz主頻的個人計算機，初值生成所用時間為22分45秒，得出最優解所用時間為14分22秒。由于所采用的軌跡優化方法利用遺傳算法進行初值生成，其優化計算效率比單純的高斯偽譜法略低，但是對于離線軌跡優化來說仍在可接收的范圍之內。電動帆航天器自地球－火星飛行軌跡如圖4所示，若電動帆航天器于2030年8月3日離開地球影響球，將歷時879天于2032年12月29日抵達谷神星引力影響范圍。由電動帆航天器自地球至谷神星的控制變量－時間曲線(圖5)可以看出，混合優化算法得出的控制變量能夠滿足控制變量約束，且變化相對平緩，利于工程實現。

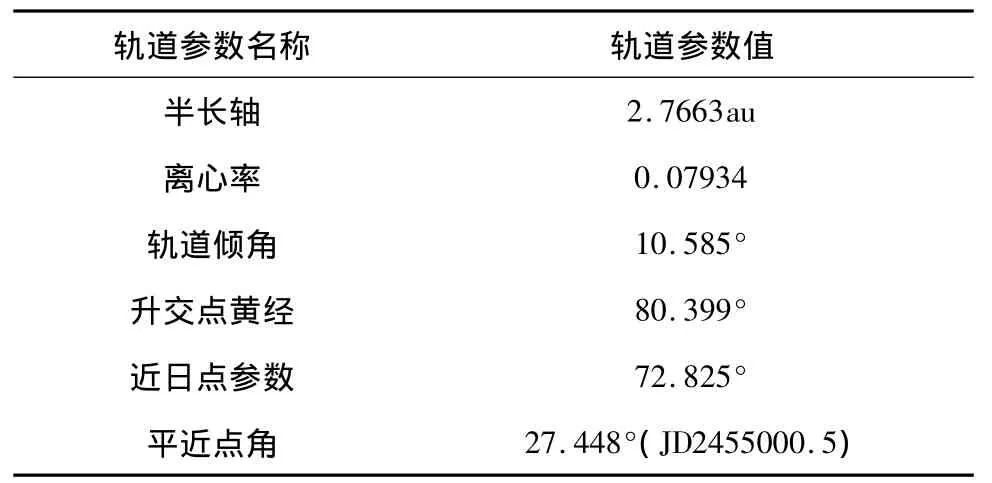
表1 谷神星軌道參數Table 1 Orbital parameters of Ceres

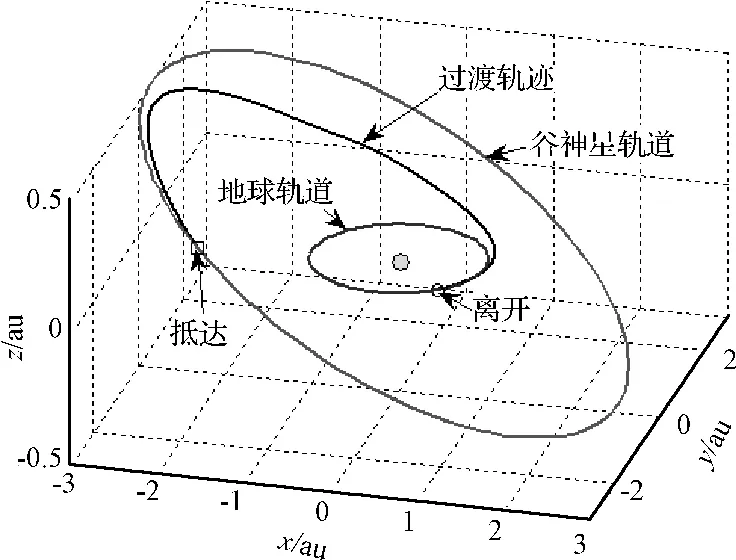
圖4 地球－谷神星過渡軌跡(a⊕=1 mm/s2)Fig．4 Earth－Ceres optimal transfer trajectory(a⊕=1 mm/s2)

為了驗證軌跡優化算法的精度，將所得到的控制變量插值后代入到控制模型中進行積分。積分公式為四階－五階龍哥庫塔積分公式，積分函數為ode45，積分相對精度為10－9，積分得出的狀態變量結果繪制于圖6和圖7。由這兩個圖可以看出，混合優化算法得到的軌跡與相同控制變量積分得到的軌跡差別較小(在圖6和圖7中兩條軌跡都已畫出，積分軌跡為實線，優化得出的原軌跡為虛線，但是兩者在圖中過于接近已經基本重合)。這是由于高斯偽譜法所采用的高斯積分公式具有較高的精度，這也正是高斯偽譜法近年來得到相關學者重視的一個原因。通過積分結果對交會處的相對位置和相對速度進行分析，位置終端誤差為35616 km，小于谷神星的引力球半徑(約為47000 km);速度終端誤差為23．526 m/s，相對谷神星的逃逸能量小于零，能夠實現與谷神星的交會。在真實的任務軌跡優化中，可通過增加高斯偽譜法的LG點個數來進一步提高交會精度。

圖5 控制變量－時間曲線(a⊕=1 mm/s2)Fig．5 Time histories of the control variables(a⊕=1 mm/s2)

圖6 位置矢量－時間曲線(a⊕=1 mm/s2)Fig．6 Time histories of the position vector(a⊕=1 mm/s2)

圖7 速度矢量－時間曲線(a⊕=1 mm/s2)Fig．7 Time histories of the velocity vector(a⊕=1 mm/s2)

3．2起始時間對探測任務的影響

為了進一步驗證混合優化算法的有效性以及考察起始時間t0對探測任務的影響，本節對不同起始時間情況下電動帆航天器自地球至谷神星的飛行軌跡進行優化。本節中起始時間t0不作為設計變量，而是自2020年1月1日(JD2458849．5)到2030年12月31日(JD2462866．5)每30天為兩個仿真的時間間隔進行指定起始時間的軌跡優化，共計134個軌跡優化算例，其余仿真參數均與上一節一致，飛行時間(tf－t0)總結在圖8中。

由圖8可以看出，電動帆航天器自地球至谷神星的飛行時間隨著起始時間的變化呈周期性波動，在3720天內共波動8次，平均變化周期為465天，這一數值與谷神星和地球的會合周期466．7天十分接近。出現這種現象的原因是當電動帆航天器從地球軌道到達谷神星軌道時，谷神星也必須同時達到，才能使航天器與谷神星實現交會。所以航天器發射時地球與谷神星的相對位置將直接影響飛行所需時間，而兩者相對位置近似成周期性變化，變化周期既是谷神星和地球的會合周期。這就是電動帆航天器自地球至谷神星飛行時間變化周期與交會周期相近的原因。另外，由于谷神星軌道傾角及偏心率等因素的影響，相鄰波動段內的飛行時間并不完全相等，而是存在一定差異。

圖8 不同起始時間情況下的最小飛行時間(a⊕=1 mm/s2)Fig．8 Minimum transfer time as a function of the starting date(a⊕=1 mm/s2)

3．3特征加速度對探測任務的影響

為了考察電動帆航天器特征加速度a⊕對所需飛行時間的影響，以不同特征加速度下電動帆自地球至谷神星的過渡軌跡進行了優化計算。考慮的特征加速度范圍為0．4 mm/s2～2 mm/s2，每個仿真之間的特征加速度間隔為0．1 mm/s2，其余仿真參數與第3．1節中一致。不同電動帆特征加速度下地球－谷神星過渡時間如圖9所示，電動帆航天器的特征加速度越小，完成過渡所需要的飛行時間越長。當特征加速度小于0．6 mm/s2時，飛行時間有顯著的增加。通過對軌跡的分析可知，航天器在自地球至谷神星的過渡過程中可粗略的劃分成兩個調整任務，即軌道半長軸的增大和軌道傾角的調整。電動帆特征加速度的大小對軌道半長軸調整所用時間影響較大，而對軌道傾角調整時間影響相對較小。當電動帆加速度大于0．6 mm/s2時，軌道半長軸調整任務先完成，影響任務完成時間的主要限制為軌道傾角的調整，所以過渡所用時間變化相對平緩。當電動帆加速度小于0．6 mm/s2時，軌道傾角調整任務先完成，影響任務完成時間的主要限制為軌道半長軸的增長，所以過渡所用時間變化相對較大。

考慮一個依據現有技術比較合理的電動帆特征加速度a⊕=0．6 mm/s2，電動帆航天器將歷時1014天完成自地球至谷神星的過渡，比采用電推進技術的黎明號空間探測器(歷時1388天完成自地球至灶神星的過渡，之后又歷時約920天完成自灶神星至谷神星的過渡)所用時間較短。不僅如此，由于電動帆在飛行過程中不消耗任何推進劑，所以在完成上述任務后仍可繼續進行其他飛行任務，如取樣返回和其他天體探測，甚至太陽系邊界探測等，減少飛行任務成本。

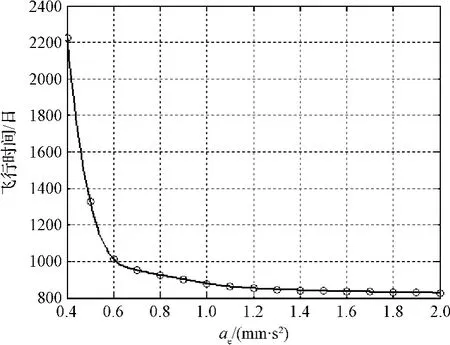
圖9 不同特征加速度情況下的最小飛行時間Fig．9 Minimum transfer time as a function of the characteristic acceleration

通過以上的軌跡優化算例可知，所提出的混合優化算法是有效的，能夠在無任何初值猜測的情況下完成電動帆航天器飛行軌跡的優化。另外，一個具有中等特征加速度的電動帆航天器便能在可接受的時間內完成自地球至谷神星的過渡，所以電動帆航天器是適用于谷神星探測任務的。

4 結論

為了將來能更快更廉價地對谷神星進行探測，提出將電動帆推進技術應用于谷神星探測任務中。并提出一種結合高斯偽譜法和遺傳算法的混合優化算法對電動帆自地球至谷神星的軌跡進行了優化。數學仿真結果表明:1)電動帆航天器自地球至谷神星的飛行時間隨著起始時間的變化成周期性波動，波動周期基本與地球－谷神星會合周期基本一致;2)電動帆航天器的特征加速度越小，完成過渡所需要的飛行時間越長，且一個具有中等特征加速度的電動帆航天器便能在可接受的時間內完成自地球至谷神星的過渡;3)所提出的混合優化算法是有效的，能夠在無任何初值猜測的情況下完成電動帆航天器飛行軌跡的優化，避免了單純高斯偽譜法初值賦值繁瑣的問題。

［1］Petit J，Morbidelli A．The primordial excitation and clearing of the asteroid belt［J］．Icarus，2001，153(2):338–347．

［2］McCord T B，Sotin C．Ceres:evolution and current state［J］．Journal of Geophysical Research，2005，110(E5):1－14．

［3］ZOL新聞中心．太陽系第二大“蓄水池”谷神星或存在外星生命［EB/OL］．2015－01－02［2015－01－02］．http://news．zol．com．cn/article/368722．html．

［4］Rayman M D，Mase R A．Dawn's operations in cruise from Vesta to Ceres［J］．Acta Astronautica，2014，103:113－118．

［5］Zubrin M，Andrews G．Magnetic sails and interplanetary travel［J］．Journal of Spacecraft and Rockets，1991，28(2):197–203．

［6］Janhunen P．Electric sail for spacecraft propulsion［J］．Journal of Propulsion and Power，2004，20(4):763–764．

［7］Janhunen P．Status report of the electric sail in 2009［J］．Acta Astronautica，2011，68(5－6):567－571．

［8］Janhunen P．The electric solar wind sail status report［C］．European Planetary Science Congress，Rome，Italy，Sep 19－24，2010．

［9］Mengali G，Quarta A A，Janhunen P．Electric sail performance analysis［J］．Journal of Spacecraft and Rockets，2008，45(1):122－129．

［10］Quarta A A，Mengali G．Electric sail mission analysis for outer solar system exploration［J］．Journal of Guidance Control and Dynamics，2010，33(3):740－755．

［11］Quarta A A，Mengali G，Janhunen P．Optimal interplanetary rendezvous combining electric sail and high thrust propulsion system［J］．Acta Astronautica，2011，68(5－6):603－621．

［12］Mengali G，Quarta A A，Janhunen P．Considerations of electric sailcraft trajectory design［J］．Journal of British Interplanetary Society，2008，61(8):326－329．

［13］Mengali G，Quarta A A．Escape from elliptic orbit using constant radial thrust［J］．Journal of Guidance Control and Dynamics，2009，32(3):1018–1022．

［14］ 齊乃明，霍明英，袁秋帆．電動帆軌跡優化及其性能分析［J］．宇航學報，2013，34(5):634－641．［Qi Nai-ming，Huo Ming-ying，Yuan Qiu-fan．The electric sail trajectory optimization and performance analysis［J］．Journal of Astronautics，2013，34(5):634－641．］

［15］Janhunen P．Increased electric sail thrust through removal of trapped shielding electrons by orbit chaotisation due to spacecraft body［J］．Annales Geophysica，2009，27(8):3089－3100．

［16］Standish E M．JPL planetary and lunar ephemerides，DE405/LE405［EB/OL］．2008［2008］．http://iau-com m4．jpl．nasa．gov/de405iom/de405iom．pdf．

［17］David B．A Gauss pseudospectral transcription for optimal control［D］．Cambridge:Massachusetts Institute of Technology，2005．

［18］ 唐國金，羅亞中，雍恩米．航天器軌跡優化理論、方法及應用［M］．北京:科學出版社，2011:149－151．

［19］Gill P E，Murray W，Saunders M A．User’s guide for SNOPT V7:software for large-scale nonlinear programming［EB/OL］．2008［2008］．http://ccom．ucsd．edu/～peg．

［20］Gill P E，Murray W．SNOPT:an SQP algorithm for large-scale constrained optimization［J］．SIAM Journal on Optimization，2002，12(4):979–1006．