考慮跟蹤制導的小天體著陸軌跡閉環優化方法

胡海靜，高 艾，朱圣英，崔平遠

(1．北京理工大學宇航學院，北京100081;2．深空自主導航與控制工信部重點實驗室，北京100081;3．飛行器動力學與控制教育部重點實驗室，北京100081)

0 引言

小天體探測作為人類了解太陽系形成與演化、生命起源與進化以及防御外來天體撞擊的重要途徑，是深空探測的重要內容之一。對小天體的近距離探測始于20世紀90年代，伴隨著空間技術水平的快速提高，探測方式也由飛越探測向繞飛、著陸和采樣返回發展。小天體著陸探測任務的開展有助于對目標星進行實地、長期考察，獲得更多精確可靠的數據;同時，小天體著陸技術是小天體采樣返回任務成功實施的基礎，有助于將小天體的土壤和巖石帶回地球進行深入研究［1－2］。

目前，人類已成功實施兩次小天體著陸探測任務。2001年，美國宇航局(NASA)的近地小行星交會任務(Near Earth Asteroid Rendezvous，NEAR)成功在Eros433著陸［3］。2005年，日本宇航局(JAXA)的隼鳥號成功在Itokawa小天體著陸，并首次實現從小天體采樣并返回地球［4］。另外，2014年，羅塞塔任務實現在彗星67P/Churyumov-Gerasimenko表面著陸。然而，由于錨定系統故障，著陸器Philae號與小天體表面碰撞，由于小天體引力非常弱，Philae號碰撞后發生彈跳，并最終穩定在陰影區，導致其太陽能電池板無法充電，從而處于休眠狀態。其著陸與彈跳過程如圖1所示，該過程顯示，僅僅1 m/s的速度誤差導致Philae號碰撞后兩個小時處于彈跳狀態，并引發無法正常啟動的嚴重后果，表明小天體著陸精度，尤其是著陸速度誤差對任務設計非常關鍵，需要盡可能提高小天體著陸精度。

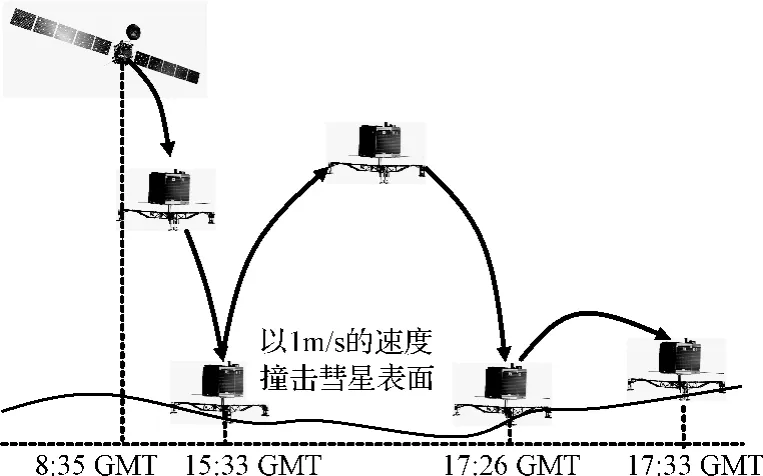
圖1 Philae號附著過程示意圖Fig．1 Illustration of the landing process of Philae

然而，著陸小天體動力學存在的參數不確定性(小天體自旋角速度及推力大小和方向偏差等)和探測器的初始狀態偏差對著陸誤差有不可忽視的影響。另外，小天體形狀不規則導致小天體附近的引力場也非常不規則，導致探測器運動規律較為復雜。以上兩方面因素導致在小天體表面成功實現精確著陸非常困難。Broschart等學者針對小天體著陸開環控制策略進行了研究，結果表明，在能對小天體進行精確建模以及對探測器狀態進行精確估計的基礎上，開環控制策略能夠用于小天體著陸任務［5－6］。然而，在任務設計階段往往無法完全確知目標天體參數及初始狀態存在的偏差，實施小天體著陸開環控制策略會引起較大的著陸誤差，存在較大任務風險。針對無法獲得精確動力學模型問題，文獻［7］給出一種利用Gauss-Markov過程的小天體著陸導航與制導算法，該方法采用一階Gauss-Markov過程近似著陸探測器軌道動力學中的無模型加速度，利用擴展卡爾曼濾波估計探測器的位置、速度及無模型加速度。另外，文獻［8］提出一種光學導航方案，利用光學相機實現特征點的提取和跟蹤，并采用激光測距儀實現矢量測量，達到提高探測器狀態估計精度的目標。在此基礎上，學者通過設計反饋制導律能夠降低跟蹤誤差［9－11］。然而，該過程忽略了著陸軌跡對跟蹤效果的影響，跟蹤不同著陸軌跡對著陸誤差有一定影響。研究表明，燃料最優著陸軌跡的推力呈現bang-bang形式［12－14］。在存在參數不確定性和初始狀態偏差的情況下，跟蹤bang-bang推力形式的最優著陸軌跡極易引起控制系統的飽和，從而影響著陸精度的提高。

針對參數不確定性和初始狀態偏差的影響，學者對航天器軌跡不確定性的非線性遞推方法進行了研究［15－16］，該方法有助于分析參數不確定性隨非線性動力學的變化過程，但因計算量大而難以在著陸軌跡優化中直接應用。文獻［17］針對星際轉移任務中初始狀態偏差的影響，在軌跡優化的過程中遞推了動力學模型的開環線性協方差，并作為優化問題的性能指標求解了最優軌跡，能夠降低初始狀態偏差的影響。文獻［18－19］分別從最優控制、軌跡優化角度推導研究了如何降低參數的敏感度。

本文以小天體著陸任務為背景，首先，建立了小天體著陸動力學模型，并分析了燃料最優著陸問題。為了更好跟蹤著陸軌跡，首先采用線性二次型調節器(Linear Quadratic Regulator，LQR)技術設計了反饋制導律，并在此基礎上推導了對不確定參數和初始狀態的閉環敏感度矩陣方程。該敏感度矩陣方程反映了閉環情況下動力學模型對參數和初始狀態的敏感程度。最后，構造了包含燃料消耗和敏感度的性能指標，并采用高斯偽譜法進行了求解。該方法綜合考慮了小天體著陸的燃料消耗和動力學模型對參數和狀態不確定性的敏感度，因而獲得的最優軌跡既能節省燃料，又能對參數和狀態偏差不敏感。

1 小天體著陸動力學與最優問題描述

1．1坐標系定義與著陸動力學

定義小天體固連坐標系Σa:坐標原點oa位于小天體的質心，za軸沿小天體自旋軸方向，xa軸沿小天體最小慣量軸方向，ya軸滿足右手系法則，如圖2所示。

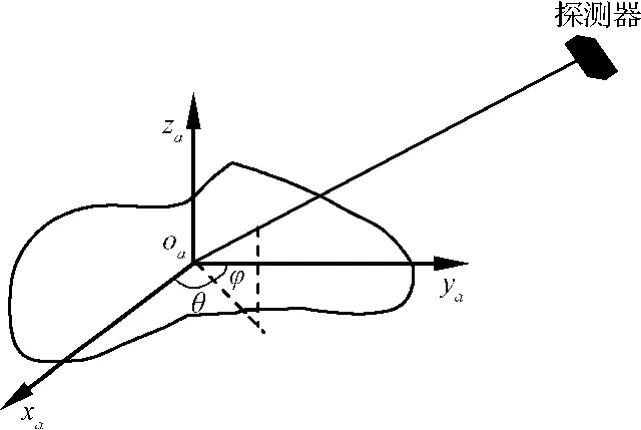
圖2 小天體固連坐標系示意圖Fig．2 Sketch map of the body-fixed coordinate frame

在小天體固連坐標系下，探測器著陸動力學方程可以表達為:

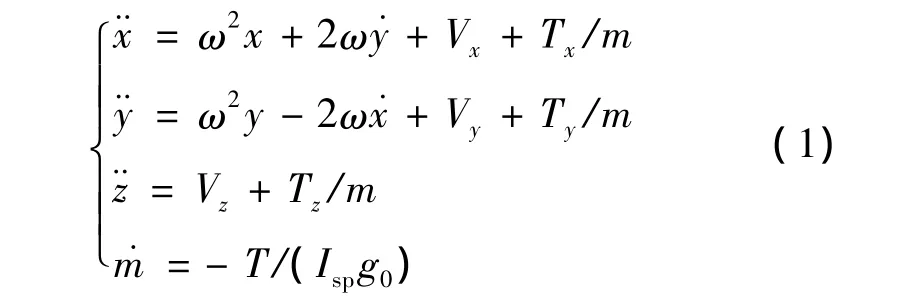
式中:x，y，z分別為探測器的三軸位置，m為探測器質量，ω為小天體的自旋角速度。Tx，Ty，Tz分別為三軸方向的控制力，其中，Tx=T cosφTcosθT，Tx=T cosφTsinθT，Tz=T sinφT，T為推力大小(Tmin≤T≤Tmax)，Tmin、Tmax分別為發動機最小和最大推力，φT和θT為推力方向角。Isp為發動機比沖，g0為地球海平面引力加速度。Vx，Vy和Vz分別為小天體引力勢函數的一階偏導數，V為小天體的引力勢函數，其四階球諧函數表達式為如下形式:

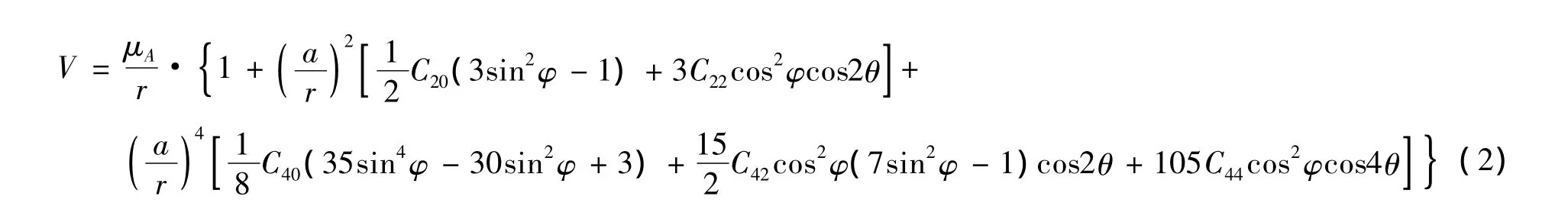
式中:μA=GM為小天體引力常數，a為小天體名義半徑，θ，φ，r分別為探測器所處經度、緯度和半徑。C20，C22，C40，C42和C44分別為引力勢函數的系數。

為了便于表達，可以將上述動力學方程寫成如下簡化形式:

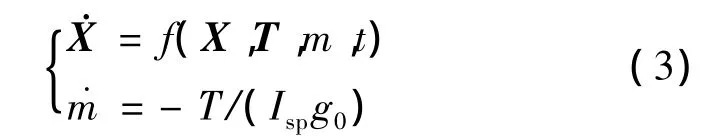
式中:X=［x y z˙x˙y˙z］T，T=［TxTyTz］T。

1．2小天體著陸優化問題描述

小天體軟著陸是探測器從初始探測軌道上某處，經一段時間減速以速度接近零到達目標點，從而實現成功著陸。小天體著陸軌跡優化是在滿足動力學約束、初始狀態約束、末端狀態約束以及路徑約束前提下，對探測器的控制力進行優化以滿足某項性能指標。其中，燃料消耗與探測任務成本直接相關，降低燃料消耗對對星際著陸任務有重要意義。

探測器的動力學約束即為式(1)。假設初始狀態為初始軌道的某一點，約束可表達為:

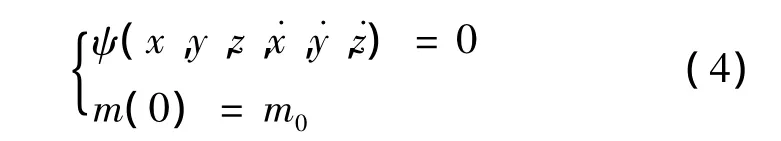
探測器終端約束為探測器終端狀態約束和終端質量約束。其中，終端狀態約束為探測器以接近為零的速度著陸到目標著陸點;終端質量約束為探測器的最終質量要超過其干重。

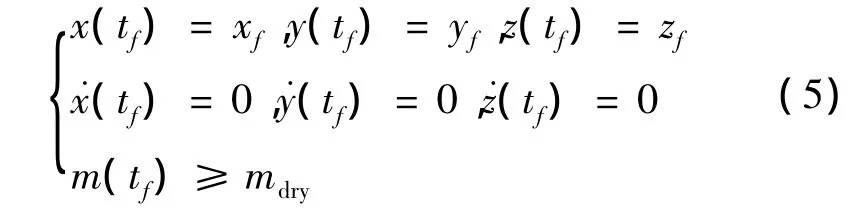
式中:tf為到達目標附著點的時刻，mdry為探測器干重，即全部燃料耗盡后的質量。

在探測器附著到小天體表面的過程中，探測器應避免與其發生碰撞，其路徑通過定義如圖3所示滑翔面約束能夠避免與小天體發生碰撞。

在滿足以上約束基礎上，對如下性能指標函數進行求解能夠獲得燃料最優著陸軌跡:

從小天體著陸動力學方程可以看出，探測器t時刻的狀態變量X(t)與其初始狀態、發動機推力加速度、小天體自轉角速度有關，即

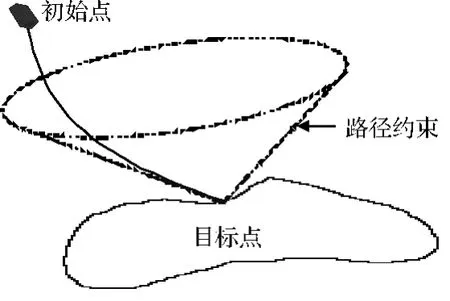
圖3 小天體著陸路徑約束Fig．3 Path constraint for landing on small bodies

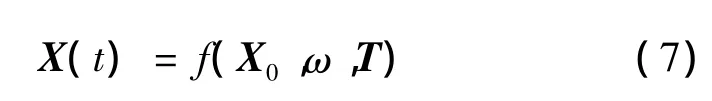
式中:X0為探測器初始狀態。然而在任務設計階段無法完全獲知小天體的動力學參數，另外，探測器實施著陸任務時的初始狀態及推力器的大小和方向均存在一定程度的偏差。如果忽略這些參數不確定性會對著陸誤差產生一定影響，其影響的大小取決于著陸軌跡對參數的敏感度及參數誤差的大小。為了提高著陸精度，需要在優化過程中通過設計閉環制導律抑制誤差的影響。

2 小天體著陸閉環優化方法

采用標稱模型能夠較為方便的求解燃料最優軌跡，然而，動力學的參數不確定性及探測器初始狀態的偏差對著陸誤差有一定影響。對此，本節提出了一種考慮跟蹤制導的小天體著陸閉環優化方法。首先，在設計的反饋制導律基礎上推導了閉環敏感度矩陣方程，并能根據該方程求解末端狀態對不確定參數的敏感度，反映了存在反饋制導律的情況下動力學對參數和初始狀態偏差的敏感程度。通過在構造性能指標時加權考慮燃料消耗與敏感度，有望實現在節省燃料的同時對參數和狀態偏差不敏感。

2．1反饋制導律設計

為了在優化過程中求解閉環的敏感度矩陣，首先需要設計跟蹤制導律。由于優化過程需要大量調用敏感度矩陣及制導律的求解函數，為了提高效率，此處采用LQR技術設計了反饋增益。

對于LQR制導策略，性能指標取如下形式:

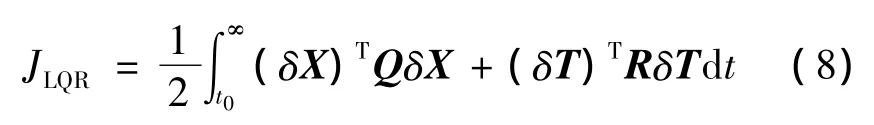
式中:δX=X－XN，δT=T－TN，下標N表示軌跡優化過程生成的標稱量。Q和R分別為正定的權重矩陣，根據Bryson原則可以取如下形式:

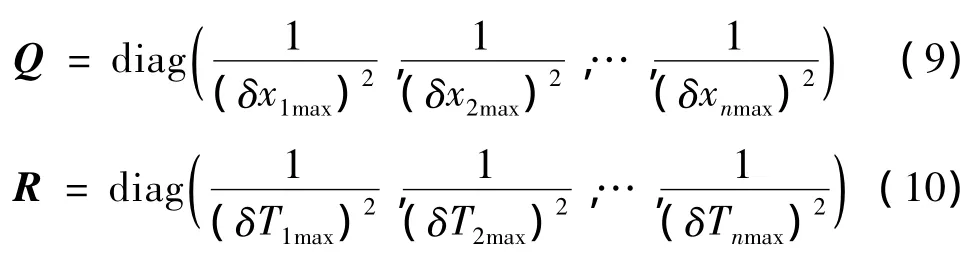
式中:δx1max，…，δxnmax和 δT1max，…，δTnmax分別為n維狀態和m維控制量的最大期望偏差。

沿標稱軌跡，可以將小天體著陸動力學做線性化處理:

式中:A和B分別為動力學的雅克比矩陣。

通過設計反饋制導律δT=－KδX可以使性能指標JLQR最小，其中，反饋控制矩陣K為:

式中P可通過求解代數黎卡提方程獲得:

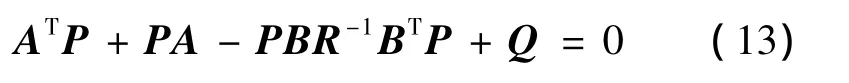
通過上述推導，反饋控制增益則可通過高效求解線性優化問題獲得。

2．2燃料/敏感度加權性能指標

在小天體著陸過程中，探測器的初始狀態、小天體的自旋角速度和推力的大小和方向的不確定性對著陸誤差有重要影響，因而，在優化過程中需要能夠降低動力學對這些參數的敏感度。

假設推力大小和方向的誤差為正態分布，則可根據隨機變量的性質將推力大小和方向的誤差轉化到三個軸方向:

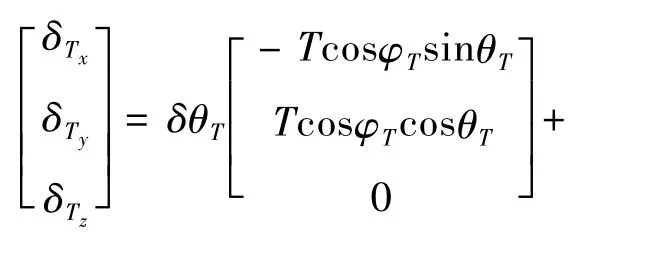
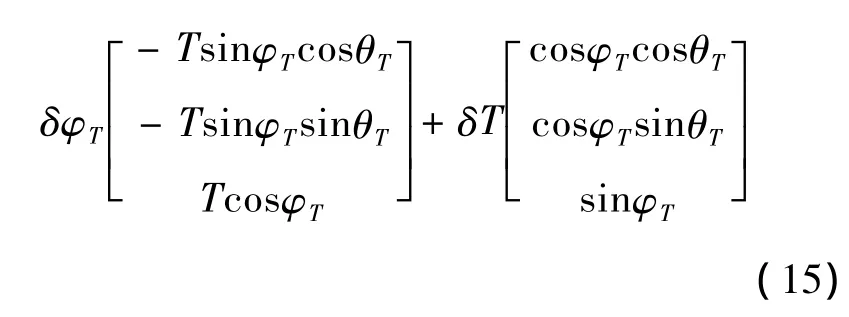
因而，小天體著陸動力學對推力偏差的敏感度向量可以表示為如下形式:

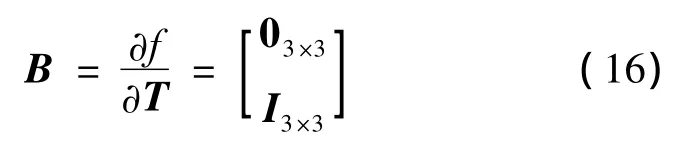
式(14)中:K為設計的反饋控制增益矩陣，η為調節系數，為實現優化過程中生成的推力避免處于最大和最小值。令T為推力向量T的大小，則η可定義為如下形式:

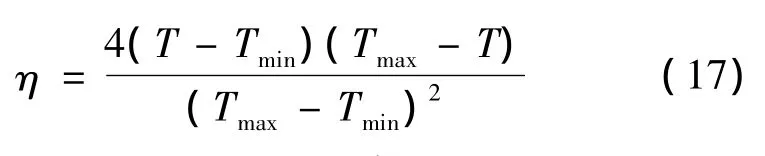
小天體著陸動力學對自旋角速度的敏感度向量如下所示:

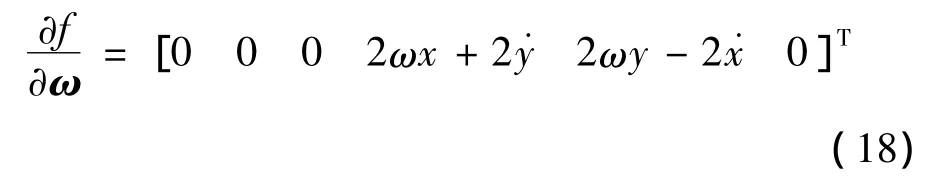
為了在優化過程中降低對參數的敏感度，需要建立含有敏感度的性能指標。本文選取如下形式的性能指標:

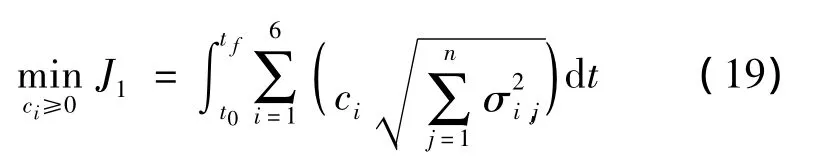
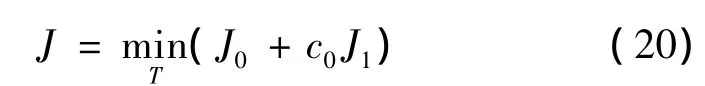
式中:c0≥0為調節敏感度和燃料的加權系數。至此，以J為性能指標進行優化，能在節省燃料的同時實現對參數不確定性不敏感。

3 仿真結果及分析

通過高斯偽譜法可以將上述軌跡優化問題轉化為非線性規劃問題，并采用SNOPT算法求解。仿真條件以Eros433小行星為目標著陸天體，其名義半徑為16 km，引力常數為4．4621×105m3/s2，密度為2．67 g/cm3，標稱自旋角速度為3．31 rad/s。選取探測器質量為300 kg，推力發動機的最大推力為

式中:n為敏感度矩陣的維數，σi，j為矩陣的第(i，j)個元素。ci，i=1，…，6為權重系數，用于平衡位置和速度的權重。

通過構建性能指標J1，則可將原燃料最優問題轉化基于燃料/敏感度加權的閉環優化問題:20 N，比沖為300 s。探測器的初始和末端條件分別如表1所示。給定條件下，采用高斯偽譜法求得小天體著陸的燃料最優軌跡如圖4所示，可以看出著陸軌跡能夠滿足初始和末端狀態以及路徑約束，其三軸速度變化過程如圖5所示，在無參數攝動情況下，著陸器能夠平穩著陸到小天體表面，到達目標點。在著陸過程中，著陸器三軸推力及其合理大小如圖6所示。從中可以看出，燃料最優著陸軌跡的合力大小為bang－bang形式。由于推力長時間處于最大邊界，在存在參數不確定性及初始狀態偏差的情況下，控制系統極易飽和，難以達到抑制偏差的目的。

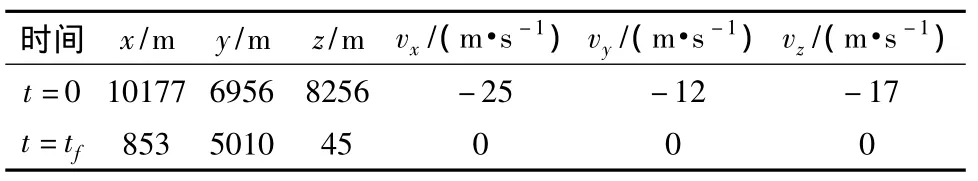
表1 邊界條件Table 1 Boundary conditions

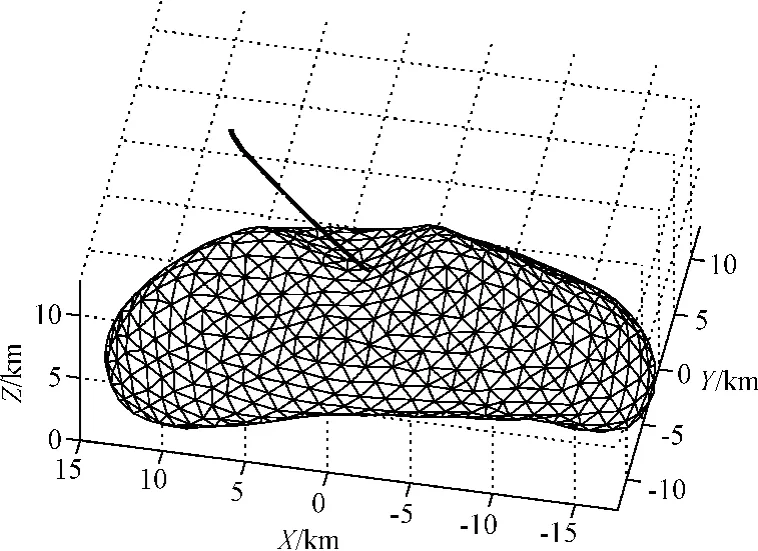
圖4 燃料最優著陸軌跡Fig．4 Fuel optimal landing trajectory

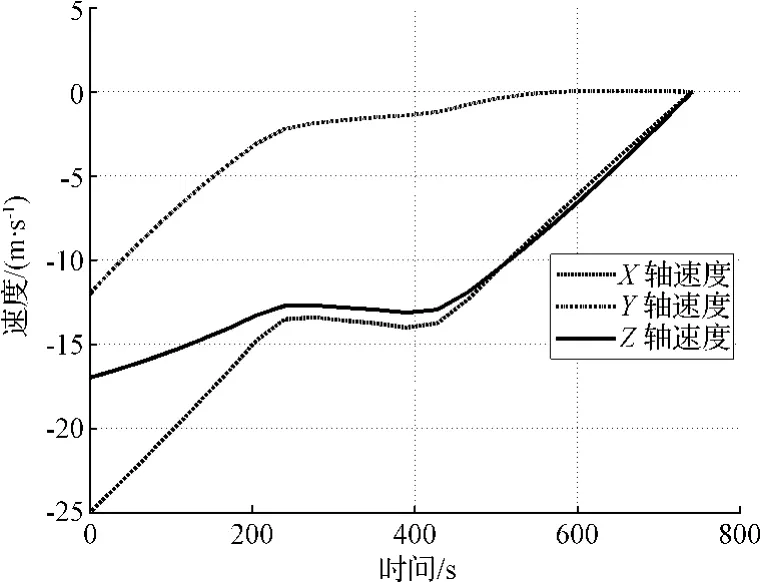
圖5 最優著陸軌跡的三軸速度Fig．5 Velocities of optimal trajectory in three axes direction

小天體著陸軌跡受參數不確定性及初始狀態偏差的影響在文獻［5］中進行了研究，著陸誤差受探測器狀態確定精度及推力器模型誤差影響較大。因而，在無法確切獲知目標天體參數及探測器狀態信息的情況下，執行開環著陸會引起非常大的著陸誤差，可能導致著陸任務的失敗。

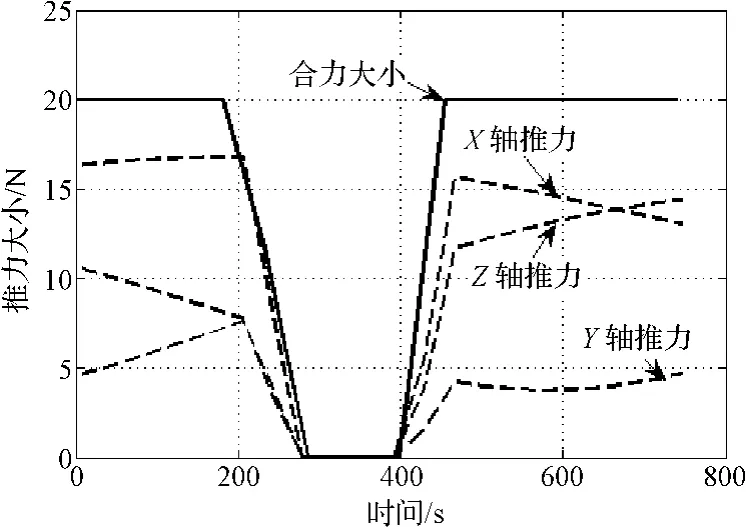
圖6 三軸推力及合力大小Fig．6 Thrust in three axes and its net thrust

引入閉環敏感度性能指標J1，則通過優化推力大小和方向能夠降低燃料消耗和敏感度，獲得的推力曲線如圖7所示，通過調節加權系數c0能夠調節敏感度性能指標J1的比重。當c0逐漸增大時，推力曲線逐漸接近遠離最大最小邊界，從而留有一定的控制余量用于抑制參數不確定性和初始狀態偏差的影響，能夠有效避免控制系統飽和，達到提高著陸精度的目標。在實際著陸任務中，需根據目標天體參數不確定性和初始狀態偏差范圍合理選取c0，達到既能節省燃料又能實現提高著陸精度的目標。

表2 狀態和參數不確定性范圍Table 2 Dispersions in states and parameters

為了校驗基于燃料/敏感度加權的閉環優化方法對參數不確定性和初始狀態偏差的抑制效果，另外進行了一組2000次Monte Carlo仿真。其中，小天體著陸動力學存在的參數不確定性及探測器初始狀態偏差范圍如表2所示。

在給定參數范圍下，最終著陸位置和速度誤差分別如圖8和圖9所示。其中，圖8為著陸位置誤差結果，其3σ 誤差橢圓為0．21 m×0．68 m，能夠滿足小天體精確著陸的位置精度要求。另外，小天體引力非常小，較大的速度與小天體表面碰撞可能使得達到小天體的逃逸速度，因而小天體著陸任務對著陸速度誤差有非常高的要求。圖9所示的著陸速度顯示最終的著陸速度均小于0．1 m/s，能夠滿足在小天體表面著陸的速度要求。

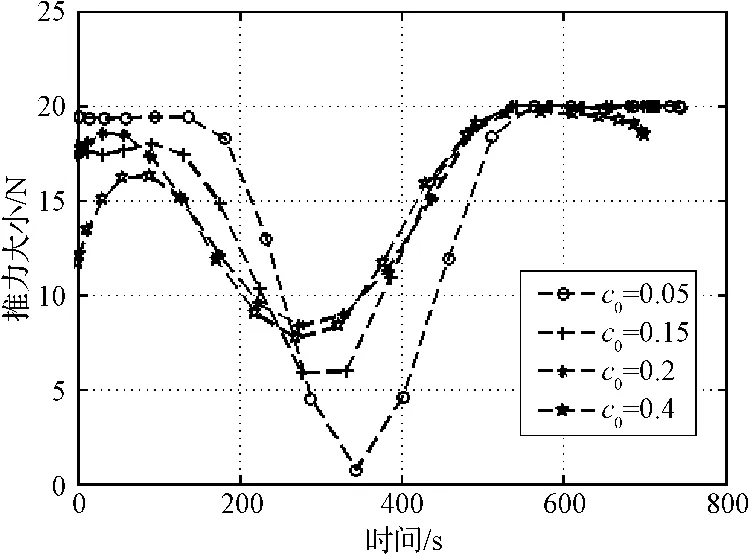
圖7 著陸軌跡的推力大小Fig．7 Thrust magnitude of optimal trajectory

圖8 著陸位置誤差及誤差橢圓Fig．8 Position error and its error ellipse

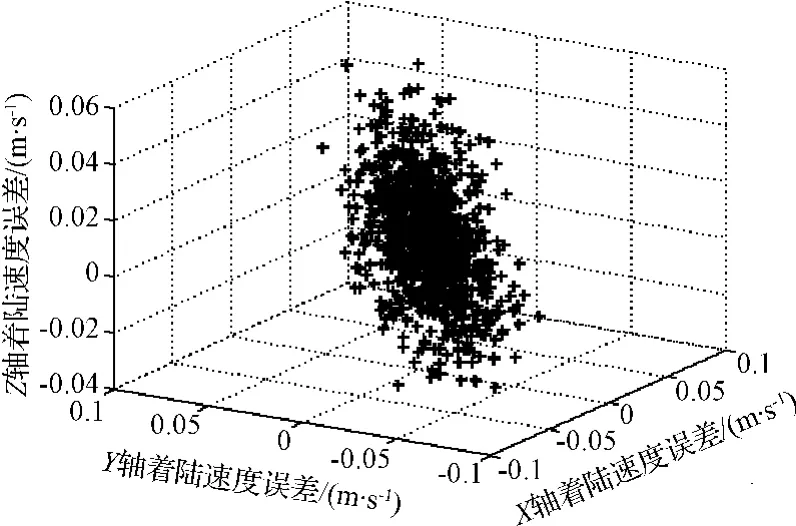
圖9 三軸著陸速度誤差Fig．9 Velocity error in three axes

4 結束語

本文針對小天體著陸動力學存在的參數不確定性及探測器初始狀態的偏差對著陸誤差的影響，提出了一種考慮跟蹤制導的小天體著陸閉環優化方法。該方法綜合考慮了小天體著陸的燃料消耗和動力學模型對參數和狀態不確定性的敏感度，能夠實現著陸過程既節省燃料，又降低參數和狀態不確定性的敏感度。仿真結果顯示，在給定參數不確定性和初始狀態偏差條件下，跟蹤著陸軌跡的3σ位置誤差橢圓為0．21 m×0．68 m，速度誤差均小于0．1 m/s，能夠滿足小天體精確著陸的任務要求。

［1］ 崔平遠，喬棟，朱圣英，等．行星著陸探測中的動力學與控制研究進展［J］．航天器環境工程，2014，31(1):1－8．［Cui Ping-yuan，Qiao Dong，Zhu Sheng-ying，et al．Research progress of dynamics and control for planetary landing［J］．Spacecraft Environment Engineering，2014，31(1):1－8．］

［2］ 喬棟，黃江川，崔平遠，等．嫦娥二號衛星飛越探測小行星的目標選擇［J］．中國科學:技術科學，2013，43(6):602－608．［Qiao Dong，Huang Jiang-chuan，Cui Ping-yuan，et al．Target selection to fly by asteroid exploration for Chang’E－2 mission［J］．Science China Technological Sciences，2013，43(6):602–608．］

［3］Cheng A F，Santo A G，Heeres K J．Near-Earth Asteroid Rendezvous:mission overview［J］．Journal of Geophysical Research:Planets，1997，102(10):23695–23708．

［4］Yoshimitsua T，Kawaguchia J，Hashimotoa T．Hayabusa-final autonomous descent and landing based on target marker tracking［J］．Acta Astronautica，2009，65(5):657－665．

［5］Broschart SB，Scheeres D J．Spacecraft descent and translation in the small-body fixed frame［C］．AIAA/AAS Astrodynamics Specialist Conference，Rhode Island，August 16－19，2004．

［6］ 袁旭，朱圣英，喬棟，等．小天體著陸動力學參數不確定性影響分析［J］．深空探測學報，2014，1(2):134－139．［Yuan Xu，Zhu Sheng-ying，Qiao Dong，et al．Impact analysis of dynamic parameters uncertainty on small celestial body landing［J］．Journal of Deep Space Exploration，2014，1(2):134－139．］

［7］ 黃翔宇，崔平遠，崔祜濤，等．利用Gauss-Markov過程的著陸小天體導航與制導方法［J］．宇航學報，2004，25(3):338-342．［Huang Xiang-yu，Cui Ping-yuan，Cui Hu-tao，et al．A navigation and guidance method for small celestial body landing using Gauss-Markov process［J］．Journal of Astronautics，2004，25(3):338－342．］

［8］ 崔平遠，朱圣英，崔祜濤．小天體軟著陸自主光學導航與制導方法研究［J］．宇航學報，2009，30(6):2159－2164．［Cui Ping-yuan，Zhu Sheng-ying，Cui Hu-tao．Autonomous optical navigation and guide method for soft landing on small bodies［J］．Journal of Astronautics，2009，30(6):2159－2164．］

［9］Furfaro R，Cersosimo D，Wibben D R．Asteroid precision landing via multiple sliding surfaces guidance techniques［J］．Journal of Guidance，Control，and Dynamics，2013，36(4):1075－1092．

［10］ 崔平遠，朱圣英，崔祜濤．小天體自主軟著陸脈沖機動控制方法研究［J］．宇航學報，2008，29(2):511－516．［Cui Ping-yuan，Zhu Sheng-ying，Cui Hu-tao．Autonomous impulse maneuver control method for soft landing on small bodies［J］．Journal of Astronautics，2008，29(2):511－516．］

［11］Carson J M，Acikmese B，Murray R M，et al．A robust model predictive control algorithm augmented with a reactive safety mode［J］．Automatica，2013，49(5):1251－1260．

［12］Lantoine G．Optimal trajectories for soft landing on asteroids［R］．MS Special Problems Report，Georgia Institute of Technology，Atlanta，2006．

［13］ 江秀強，陶婷，楊威，等．附著小天體的最優制導控制方法［J］．深空探測學報，2015，2(1):53－60．［Jiang Xiu-qiang，Tao Ting，Yang Wei，et al．Optimal guidance control strategies for spacecraft attaches to a small body［J］．Journal of Deep Space Exploration，2015，2(1):53－60．］

［14］ 任高峰，高艾，崔平遠，等．一種燃料最省的火星精確著陸動力下降段快速軌跡優化方法［J］．宇航學報，2014，35(12):1350－1358．［Ren Gao-feng，Gao Ai，Cui Ping-yuan，et al．A rapid power descent phase trajectory optimization method with minimum fuel consumption for Mars pinpoint landing［J］．Journal of Astronautics，2014，35(12):1350－1358．］

［15］Avinash P，James F，Raktim B．Polynomial chaos-based analysis of probabilistic uncertainty in hypersonic flight dynamics［J］．Journal of Guidance，Control，and Dynamics，2010，33(1):222－234．

［16］Park R S，Scheeres D J．Nonlinear mapping of Gaussian statistics:theory and applications to spacecraft trajectory design［J］．Journal of Guidance，Control，and Dynamics，2006，29(6):1367－1375．

［17］Zimmer SJ．Reducing spacecraft state uncertainty through indirect trajectory optimization［D］．Austin:The University of Texas at Austin，2005．

［18］Kreindler E．Formulation of minimum trajectory sensitivity problem［J］．IEEE Transactions on Automatic Control，1969，14(2):206–207．

［19］Seywald H，Kumar R R．Desensitized optimal trajectories［J］．Advances in the Astronautical Sciences，1996，93(1):103－116．