考慮航線交叉的救援直升機起飛時序規(guī)劃方法*
張家銘,劉 忠,石建邁,賀云岳,王一杉,陳 超
(1.國防科技大學(xué) 信息系統(tǒng)與管理學(xué)院, 湖南 長沙 410073; 2.中國人民解放軍63796部隊, 四川 西昌 615000)
?
考慮航線交叉的救援直升機起飛時序規(guī)劃方法*
張家銘1,劉忠1,石建邁1,賀云岳1,王一杉2,陳超1
(1.國防科技大學(xué) 信息系統(tǒng)與管理學(xué)院, 湖南 長沙410073; 2.中國人民解放軍63796部隊, 四川 西昌615000)
摘要:為解決多架救援直升機的起飛時序規(guī)劃問題,以最小化最后一架救援直升機的起飛時間為優(yōu)化目標,建立多直升機多起降點的數(shù)學(xué)規(guī)劃模型。設(shè)計了基于任務(wù)優(yōu)先級的快速啟發(fā)式算法,提出航線交叉點的處理方案,給出起飛時間求解算法。以云南魯?shù)?.8級地震的災(zāi)后救援為背景,設(shè)計了包含24架直升機和12個起飛點的起飛時序規(guī)劃案例,對模型和算法進行了仿真驗證,并對航線交叉的影響與處理措施進行了深入討論。實驗結(jié)果表明該模型和方法能有效解決多架救援直升機的起飛時序規(guī)劃問題。
關(guān)鍵詞:災(zāi)害救援;救援直升機;任務(wù)規(guī)劃;航線交叉
中國是自然災(zāi)害多發(fā)的國家,近年來發(fā)生的地震、塌方、泥石流等重大自然災(zāi)害,給國家和人民生命財產(chǎn)帶來了巨大損失。以地震災(zāi)害為例,據(jù)中國地震局統(tǒng)計,中國大陸地震約占世界大陸地震總數(shù)的1/3,而死亡人數(shù)約占世界地震死亡人數(shù)的1/2[1]。導(dǎo)致地震等自然災(zāi)害中死亡人數(shù)居高不下的一個重要原因就是災(zāi)后交通受阻以致救援不及時[2]。直升機可以垂直起降,可以更快到達水、陸路不可通達的作業(yè)現(xiàn)場和受災(zāi)嚴重地區(qū),因而成為災(zāi)害救援的核心裝備。因此,為了進一步提高救援效率,保障飛行安全,縮短救援時間,為各航路的救援直升機合理地規(guī)劃起飛時序意義重大。相關(guān)研究主要集中在以下兩方面的問題。
直升機的航路規(guī)劃問題。主要是研究在滿足一定約束條件下,如何尋找直升機從初始點到目標點的最優(yōu)運動軌跡[1]。常用的優(yōu)化目標有運動時間最短[3]、離地高度最低[1]等。航路規(guī)劃問題本質(zhì)是路徑搜索問題,根據(jù)對搜索狀態(tài)空間的劃分和搜索算法的特點,文獻[1]將航路規(guī)劃方法歸納為三種:一是基于概略圖的規(guī)劃方法,常用的有泰森多邊形法[4]、隨機路線圖法[5];二是基于單元分解的規(guī)劃方法,常用的求解算法有A*算法[6]和動態(tài)規(guī)劃算法[7-8]等;三是基于類比的航路規(guī)劃方法,典型的算法有人工勢場法[9]、神經(jīng)網(wǎng)絡(luò)算法[10]、蟻群算法[11-13]、遺傳算法[14]等。
直升機的任務(wù)規(guī)劃問題。主要是研究直升機在執(zhí)行醫(yī)療物資投放、搶險力量輸送、受傷民眾疏散等救援任務(wù)過程中,滿足救援時間窗口和飛行時間等約束的前提下,尋求最優(yōu)的資源調(diào)配方案[15]。常用的優(yōu)化目標有執(zhí)行救援任務(wù)的總時間最短[16]、物資分發(fā)后的最小獲得物資量最大[17]。相關(guān)研究對于災(zāi)害救援過程中直升機等救援裝備的合理調(diào)配具有指導(dǎo)意義。
此外,飛行器的自身安全也是一個不容忽視的問題,尤其是近年來世界多地發(fā)生的直升機相撞事故使得直升機的飛行安全再度引起人們的關(guān)注。2012年2月22日,美海軍陸戰(zhàn)隊兩架直升機在亞利桑那州尤馬縣訓(xùn)練基地演習時相撞,事故造成七名海軍陸戰(zhàn)隊員身亡[18]。2013年3月21日,德國兩架警用直升機在柏林上空相撞墜毀,造成至少一名飛機駕駛員死亡,多人受傷[19]。類似的直升機相撞事故進一步表明,盡管直升機具備垂直起降、空中懸停等特殊性能,但假如操作不當,航線交叉的多架直升機依然有較大可能發(fā)生相撞,造成不可挽回的災(zāi)難。因此,“航線交叉”既是實際飛行中必須重視的安全因素,也是當前相關(guān)研究中不容忽視的重點問題。
1問題描述
1.1 基本概念
為便于問題描述及模型理解,先將相關(guān)概念解釋如下。
通用航空器(generic aircraft)又稱通用航空飛行器,它是指除用于軍事、警務(wù)、海關(guān)緝私飛行和公共航空運輸飛行以外的航空活動所使用的航空器[20]。本文所指的救援直升機屬于通用航空器的范疇。
航路(air route)是由民航主管當局等機構(gòu)批準建立的一條由導(dǎo)航系統(tǒng)劃定空域構(gòu)成的空中飛行通道[21]。
航線(airway)是航空器預(yù)定要飛行的路線,航空器在任何兩個地點間確定的飛行線路就是航線[21]。
交叉點(intersection)是指兩條(含)以上的航線相交的點[22]。
巡航高度層(cruising level)是指飛行器飛行的大部分時間所保持的高度層[22]。
1.2 航線交叉處理策略
一般而言,空間上的巡航高度層分離、時間上的起飛時間錯開,都是解決航空器航線交叉的重要措施。因此,為保證航空器在航線交叉點處的飛行安全,可靈活采用空間調(diào)整或時間分配的方法[22]。而對于執(zhí)行災(zāi)害救援的直升機而言,通過空間調(diào)整的方法保證交叉點處的飛行安全,存在以下局限和不足:一是直升機飛行空域受限,災(zāi)區(qū)多為山區(qū),可供直升機調(diào)整的飛行空間十分有限,往往不允許直升機做大幅度的爬升動作;二是直升機操縱性受限,在高海拔地區(qū)執(zhí)行救援任務(wù)時,隨著飛行高度的增加,空氣密度減小,直升機發(fā)動機的可用功率和旋翼的效率會降低,直升機的操縱性也會變差[23]。因此,在不影響救援任務(wù)的前提下,側(cè)重研究了時間維度的優(yōu)化,即為直升機合理分配起飛時間,而高度層和起飛時間同時優(yōu)化將是后續(xù)研究的重要擴展方向。
1.3 問題假設(shè)
為便于研究,在不影響直升機起飛時序規(guī)劃主要需求的前提下,進行如下假設(shè):
1)采用直升機的平均飛行速度來計算其飛行用時。
2)所指的救援是指直升機安全到達降落點的單向飛行,并非是直升機的往返飛行,實際救援過程中運用本文的模型和算法時,可將直升機返航過程視為新的飛行任務(wù)。
3)研究的救援直升機均沿救援指揮部及空管部門規(guī)劃的航路飛行。
2模型構(gòu)建
2.1 符號定義
I表示起飛點集合,且i=1,2,…,I。
Ji表示從起飛點i起飛的第j架直升機,且j=1,2,…,J。
K表示救援目標區(qū)集合,且k=1,2,…,K。
Lk表示救援目標區(qū)k的第l個降落點,且l=1,2,…,L。
tij_fly:起飛點i的第j架直升機飛抵目標區(qū)的飛行用時。
tij_end:起飛點i的第j架直升機飛抵目標區(qū)的時刻。
ΔTi_take-off:起飛點i連續(xù)起飛兩架直升機時的最短時間間隔。
ΔTi_safe:起飛點i連續(xù)起飛多架直升機時的安全時間范圍。
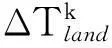
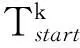
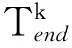
tij×i′j′:起飛點i起飛的第j架直升機飛抵航線交叉點處的飛行用時,該交叉點由起飛點i起飛的第j架直升機的航線與起飛點i′起飛的第j′架直升機的航線相交產(chǎn)生。
ti′j′×ij:起飛點i′起飛的第j′架直升機飛抵航線交叉點的飛行用時,該交叉點由起飛點i′起飛的第j′架直升機的航線與起飛點i起飛的第j架直升機的航線相交產(chǎn)生。
ΔTij×i′j′_cross:起飛點i起飛的第j架直升機與起飛點i′起飛的第j′架直升機飛經(jīng)航線交叉點的安全飛行交會時間差。
tij_start:起飛點i的第j架直升機的起飛時刻,且tij_end=tij_start+tij_fly。
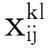
2.2 數(shù)學(xué)模型
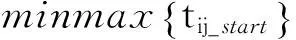
約束條件包括:
1)同一起飛點的兩架直升機的起飛時刻間隔約束,即同一起飛點連續(xù)起飛兩架直升機之間的時間間隔必須超過某一規(guī)定的安全間隔ΔTi_take-off,如式(1)所示。
tij+1_start-tij_start≥ΔTi_take-off
(1)
2)多架直升機從起飛點起飛的安全時間窗口約束,即同一起飛點的多架直升機必須在某一規(guī)定時間范圍內(nèi)起飛完畢,如式(2)所示。
tiJ_start-ti1_start≤ΔTi_safe
(2)
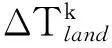
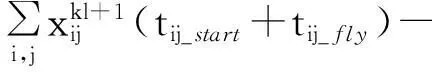
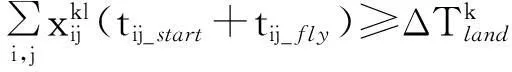
(3)
4)直升機到達每個降落點的時段約束,如某架次直升機必須在某一規(guī)定時間段內(nèi)降落到目標區(qū)k,如式(4)所示。
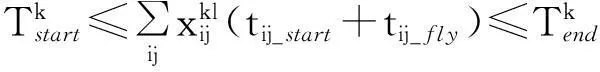
(4)
5)兩架直升機在飛行過程中,可能存在航線交叉的情況,為了飛行安全,兩架直升機到達航線交叉點的時間之差不能小于某一規(guī)定的時間間隔ΔTij×i′j′_cross,如式(5)所示。
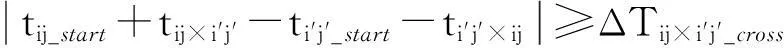
(5)
3算法設(shè)計
3.1 起飛時刻求解策略
若將起飛點和目標區(qū)抽象為有向圖中的頂點,將起飛點與目標區(qū)的匹配關(guān)系看作有向圖中的邊,則救援任務(wù)集合就可以表示成有向圖的形式。假設(shè)某救援任務(wù)有I個起飛點,每個起飛點有J架直升機,所有直升機需飛往K個救援目標區(qū)展開災(zāi)害救援,每個目標區(qū)有L個降落點,整個救援任務(wù)共設(shè)有C條飛行航線。因此,可將I個起飛點和K個救援目標區(qū)抽象成有向圖G1的頂點集合V(G1)={v1,v2,…,vI+K},將飛行航線抽象成有向圖G1的邊集合E(G1)={e1,e2,…,eC}。如前所述,航線的起飛時間受到眾多約束條件的限制,各條航線的起飛時間相互制約相互影響,當確定了某條航線的起飛時間后,其他航線起飛時間的取值范圍也可以逐步確定。
因此,本文設(shè)計了基于任務(wù)優(yōu)先級的起飛時間求解策略:
首先,根據(jù)任務(wù)緊急程度選定第c條航線(其中c=1,2,…,C)作為優(yōu)先級最高的任務(wù)最先起飛,則tc_start=0,且tc_end=0+tc_fly。
隨后,依據(jù)航線網(wǎng)絡(luò),找出與第c條航線到達目標區(qū)相同的第c′條航線(其中c′=1,2,…,C),受式(3)的約束,第c′條航線的到達時刻范圍可以確定,再根據(jù)到達時刻和起飛時刻的關(guān)系式tij_end=tij_start+tij_fly,可求出第c′條航線的起飛時刻范圍。
然后,根據(jù)式(1)和式(2)的約束,可以得到與第c′條航線起飛點相同航線的起飛時刻范圍。反復(fù)運用航線間的起降點關(guān)系和約束條件,最終可以求出所有航線的起飛時刻。
在實際的救援任務(wù)中,還可能出現(xiàn)從某個任務(wù)開始求解,不能完全遍歷所有任務(wù)的情況,即航線網(wǎng)絡(luò)是一個非連通有向圖,此時可選定所包含的子圖分別在零時刻開始執(zhí)行,再利用各子圖所示的任務(wù)間的求解順序逐步求解。
3.2 算法流程
步驟1:信息采集,數(shù)據(jù)預(yù)處理。通過地理信息系統(tǒng)快速計算直升機飛抵目標區(qū)的飛行用時。標注航線交叉點,構(gòu)建航線交叉矩陣。
步驟2:按照起飛時刻的求解策略逐步求解各任務(wù)的起飛時刻。
步驟3:將航線交叉矩陣與步驟2計算所得數(shù)據(jù)一同進行約束判斷,符合約束的解便構(gòu)成了起飛時序的可行解集合。
步驟4:從可行解中選出各組解中最大值最小的那一組,即滿足約束的所有飛行計劃中最優(yōu)的起飛時序。
算法流程如圖1所示。
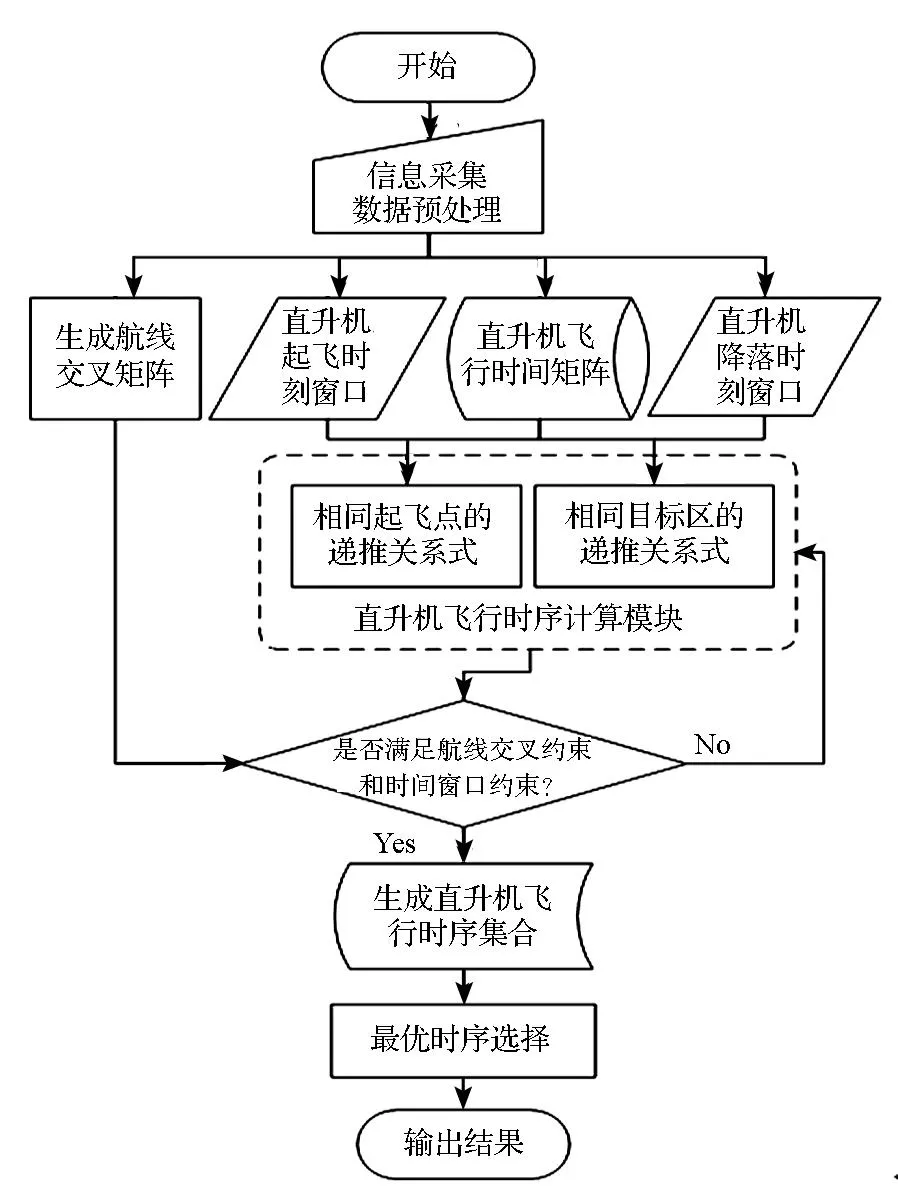
圖1 算法流程圖Fig.1 Algorithm flow chart
4仿真實驗及結(jié)果分析
4.1 仿真算例設(shè)定
以云南魯?shù)?.8級地震的災(zāi)害救援為背景。設(shè)有24架屬同一型號的救援直升機被配置在昭通市的醫(yī)院、救援物資倉庫等12個起飛點,每個起飛點配置2架救援直升機,所有直升機需飛往震中的學(xué)校、堰塞湖等12個降落點展開救援,每個降落點有2架直升機先后降落,即共有24條飛行航線。設(shè)直升機的平均飛行速度為240km/h,由此便可得到各架直升機飛抵降落點的飛行用時。為保證基本的飛行安全及任務(wù)的盡快完成,做如下要求:
1)同一起飛點的2架直升機起飛時間間隔至少大于0.5min,且不多于20min;
2)同一降落點先后降落的2架直升機降落時間間隔至少大于5min,且不多于20min;
3)對于存在交叉的飛行航線,2架直升機先后飛經(jīng)交叉點的時間間隔至少大于0.5min。
為便于分析與求解,將飛行航線抽象為有向圖G2,圖中頂點v1,v2,…,v12表示起飛點,頂點v13,v14,…,v24表示降落點,如圖2所示。
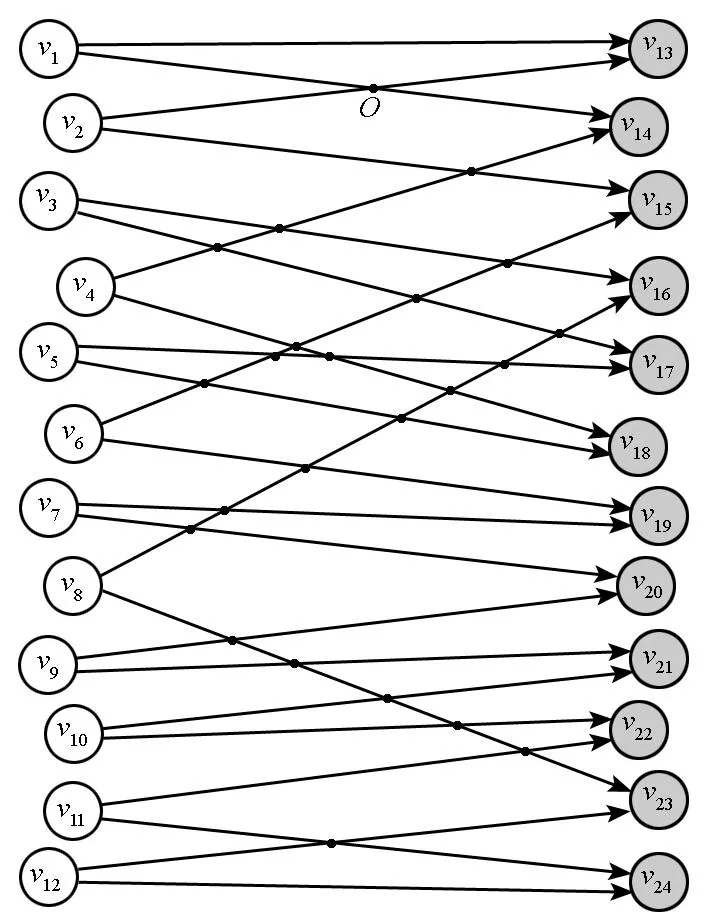
圖2 飛行航線有向圖G2Fig.2 Flight line digraph G2
4.2 仿真實驗分析
4.2.1仿真結(jié)果分析
經(jīng)過仿真計算,共得到14組最優(yōu)的起飛時序,結(jié)果列于表1中。
表1中第2欄的數(shù)字表示航線編號,如,數(shù)字“7”指代第7條航線,它具體代表航線
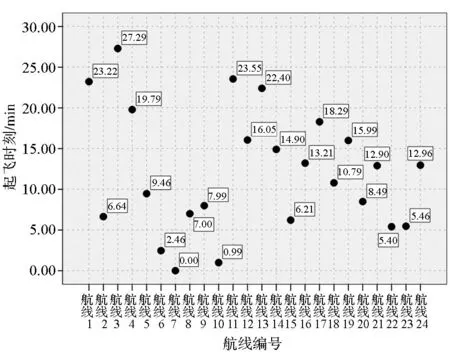
圖3 第14組起飛時序散點圖Fig.3 Scatter diagram of 14th take-off sequence

表1 最優(yōu)起飛時序表
為驗證上述結(jié)果是否滿足航線交叉約束,可將各航線的出發(fā)時間與相應(yīng)交叉點的時間屬性相結(jié)合,計算出直升機在相應(yīng)交叉點的交會時間差,檢驗結(jié)果以高低圖(high-low chart)形式展示,如圖4所示。
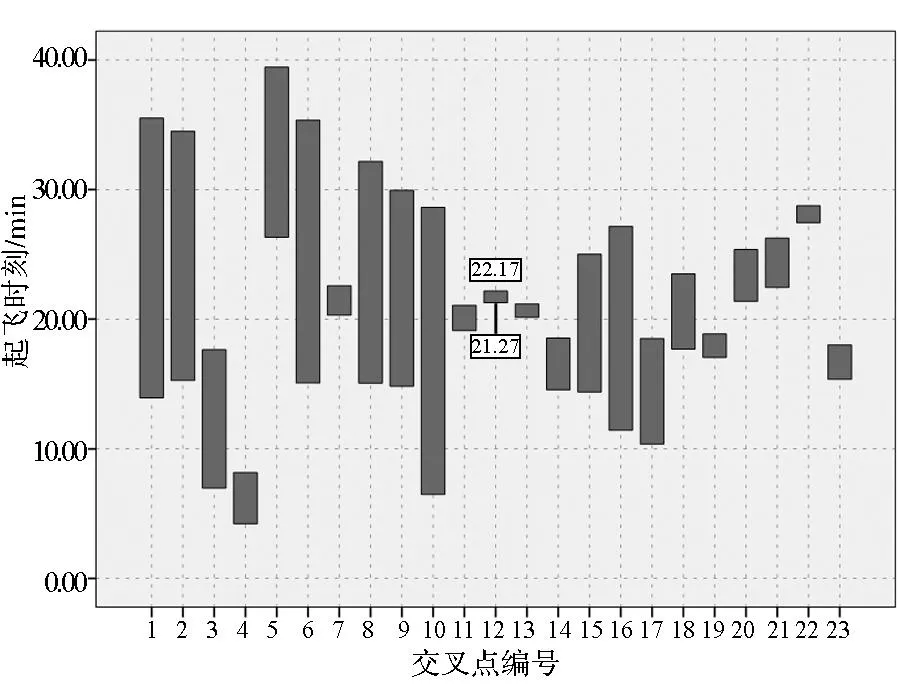
圖4 航線交叉點的交會時間高低圖Fig.4 High-low chart of meeting time
圖4中的條形(bar)表示先后飛經(jīng)某交叉點的兩架直升機的飛行時間差,條形的低值(low)表示某架直升機先飛經(jīng)該交叉點的時刻,高值(high)表示另一架直升機后飛經(jīng)該交叉點的時刻。條形長度越長說明航線交叉的兩架直升機經(jīng)過交叉點的時間間隔越長;反之則說明兩架直升機經(jīng)過交叉點的時間間隔越短,即在交叉點發(fā)生相撞的可能性越大。因此,要驗證某組起飛時序的安全性,只用檢驗長度最短的條形即可。由圖4可知,第12號交叉點對應(yīng)條形長度最短,該條形高、低值分別為22.17min和21.27min,兩者差值0.9min大于規(guī)定的安全交會時間間隔0.5min,說明航線交叉的兩架直升機在第12號交叉點處可安全通行,進而驗證了整組起飛時序的安全性。
4.2.2進一步討論
由圖2可知,航線交叉點的分布極不均勻。有的航線和其他航線不存在任何交叉點,如航線
步驟1:包含所有航線交叉點約束時,計算得最優(yōu)解(27.29min),并統(tǒng)計可行解數(shù)量(1198組)。
步驟2:不包含任何航線交叉點約束時,計算得最優(yōu)解(23.51min),并統(tǒng)計可行解數(shù)量(2584組)。
步驟3:分別考慮各條航線與其他航線存在交叉時,計算最優(yōu)解及可行解數(shù)量。
步驟4:將上述步驟得到的數(shù)據(jù)進行匯總處理。
步驟5:對步驟4得到的數(shù)據(jù)文件進行統(tǒng)計分析,統(tǒng)計描述結(jié)果如圖5所示。
由圖5(a)可知,當不包含航線交叉約束時,最后一架直升機的起飛時刻為第23.51min,而考慮了23個航線交叉點的約束后,最后一架直升機的起飛時刻推后到第27.29min。此外,隨著交叉點數(shù)量的增加,最優(yōu)解逐漸變大,特別是當單條航線與5條(含)以上航線存在交叉時,最優(yōu)解變化趨勢明顯。由圖5(b)可知,隨著交叉點數(shù)量的增加,可行解數(shù)量總體呈逐漸遞減趨勢,當單條航線與5條(含)以上航線存在交叉時,可行解數(shù)量急劇減少。
綜上,可以得到如下結(jié)論:在規(guī)劃飛行航線時,應(yīng)盡量避免航線交叉,當交叉難以避免時,應(yīng)盡量將單條航線與其他航線的交叉次數(shù)控制在5次以內(nèi)。
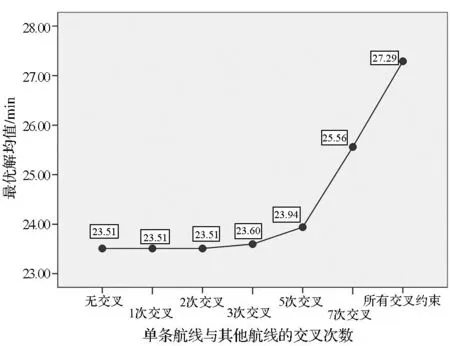
(a)交叉點約束與最優(yōu)解的關(guān)系(a) The relationship between intersection constraint and optimal solution
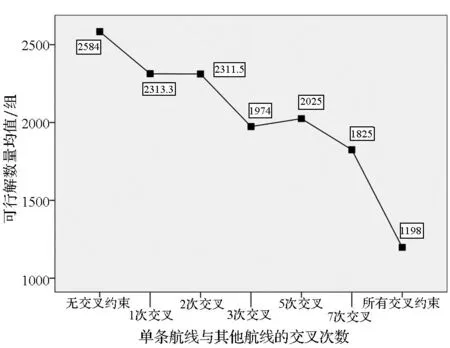
(b) 交叉點約束與可行解數(shù)量的關(guān)系(b) The relationship between intersection constraint and the number of feasible solution圖5 航線交叉約束對時序規(guī)劃的影響Fig.5 Intersection constraint’s effects on scheduling
5結(jié)論
針對救援直升機起飛時序規(guī)劃問題構(gòu)建了數(shù)學(xué)模型,并結(jié)合問題的具體特點,設(shè)計了啟發(fā)式算法進行問題求解,后以24架直升機參與地震救援為算例,對模型和算法進行了測試,并就航線交叉對于時序規(guī)劃的影響進行了分析,實驗結(jié)果顯示,本文的模型和算法能得到滿意的時序規(guī)劃方案。
下一步,將從以下方面展開進一步研究:一是在航線交叉處理策略中,加入空間調(diào)整的方法;二是在問題求解過程中,將考慮無可行解時如何給出不同約束的調(diào)整策略。
參考文獻(References)
[1]陳通. 救援直升機航跡規(guī)劃研究[D]. 廣漢:中國民用航空飛行學(xué)院, 2011.
CHEN Tong. Research on rescue helicopter route planning[D]. Guanghan: Civil Aviation Flight University of China, 2011. (in Chinese)
[2]Fiedrich F, Gehbauer F, Rickers U. Optimized resource allocation for emergency response after earthquake disasters[J]. Safety Science, 2000, 35(1/2/3): 41-57.
[3]?zdamar L, Ekinci E, Kü?ükyazici B. Emergency logistics planning in natural disasters[J]. Annals of Operations Research, 2004, 129(1): 217-245.
[4]何兵, 劉剛, 閆建靜, 等. 基于Voronoi圖和量子遺傳算法的飛行器航跡規(guī)劃方法[J]. 電光與控制, 2013, 20(1): 5-8.
HE Bing, LIU Gang, YAN Jianjing, et al. A UAV route planning method based on Voronoi diagram and quantum genetic algorithm [J]. Electronics Optics & Control, 2013, 20(1): 5-8. (in Chinese)
[5]Pettersson P O, Doherty P. Probabilistic roadmap based path planning for an autonomous unmanned helicopter[J]. Journal of Intelligent and Fuzzy Systems, 2006, 17(4) : 395-405.
[6]王志科, 朱凡, 彭建亮. 基于啟發(fā)式A*算法的飛行器三維航路規(guī)劃[J]. 電光與控制, 2009, 16(6):30-33,65.
WANG Zhike, ZHU Fan,PENG Jianliang. On 3-D path planning for air vehicle based on heuristic A*algorithm[J]. Electronics Optics & Control, 2009, 16(6): 30-33,65. (in Chinese)
[7]謝燕武, 王偉, 李愛軍. 基于有向圖的動態(tài)最優(yōu)航跡規(guī)劃算法[J]. 測控技術(shù), 2006, 25 (10) :78-81.
XIE Yanwu, WANG Wei, LI Aijun.Dynamic programming algorithm based on directed graph for optimal flight trajectory planning [J]. Measurement & Control Technology, 2006, 25(10): 78-81. (in Chinese)
[8]Yi W, ?zdamar L. A dynamic logistics coordination model for evacuation and support in disaster response activities[J]. European Journal of Operational Research, 2007, 179(3): 1177-1193.
[9]王強, 張安, 吳忠杰. 改進人工勢場法與模擬退火算法的無人機航路規(guī)劃[J]. 火力與指揮控制, 2014, 39(8): 70-73.
WANG Qiang, ZHANG An, WU Zhongjie.UCAV path planning based on improved artificial potential field and simulated annealing[J]. Fire Control & Command Control, 2014, 39(8): 70-73. (in Chinese)
[10]張岳平, 朱力超, 孫濤. 用Hopfield神經(jīng)網(wǎng)絡(luò)與模擬退火算法求解UAV航路規(guī)劃問題[J]. 海軍航空工程學(xué)院學(xué)報, 2007, 22(4): 451-453, 466.
ZHANG Yueping, ZHU Lichao, SUN Tao. UAV route planning using Hopfield neural network and simulated annealing[J]. Journal of Naval Aeronautical Engineering Institute, 2007, 22(4): 451-453, 466. (in Chinese)
[11]稅薇, 葛艷, 韓玉, 等. 基于混合蟻群算法的無人機航路規(guī)劃[J]. 系統(tǒng)仿真學(xué)報, 2011, 23(3): 574-576, 597.
SHUI Wei, GE Yan, HAN Yu, et al. Path planning for UAV based on mixed ant colony algorithm[J]. Journal of System Simulation, 2011, 23(3): 574-576, 597. (in Chinese)
[12]Balseiro S R, Loiseau I, Ramonet J. An ant colony algorithm hybridized with insertion heuristics for the time dependent vehicle routing problem with time windows[J]. Computers & Operations Research, 2011, 38(6): 954-966.
[13]Yi W, Kumar A. Ant colony optimization for disaster relief operations[J]. Transportation Research Part E: Logistics and Transportation Review, 2007, 43(6): 660-672.
[14]Shima T, Rasmussen S, Sparks A G, et al. Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms[J]. Computers & Operations Research, 2006, 33(11): 3252-3269.
[15]?zdamar L. Planning helicopter logistics in disaster relief[J]. Operational Research, 2011, 33(3): 655-672.
[17]祁明亮, 秦凱杰, 趙琰. 雪災(zāi)救援物資車輛-直升機聯(lián)合運送的調(diào)度問題研究[J].中國管理科學(xué), 2014, 22(3):59-67.
QI Mingliang, QIN Kaijie, ZHAO Yan. Research on problem of scheduling of helicopter coordinated with vehicle for resources distribution in snowstorm[J]. Chinese Journal of Management Science, 2014, 22(3): 59-67. (in Chinese)
[18]德永建.美海軍陸戰(zhàn)隊兩架直升機相撞七人身亡[EB/OL].(2012-02-24)[2014-12-12].http://www.chinanews.com/gj/2012-02-24/3694154.shtml.
DE Yongjian. The U.S. marine corps′ two helicopters collided and seven marines were killed[EB/OL].(2012-02-24)[2014-12-12]. http://www.chinanews.com/gj/2012-02-24/3694154.shtml. (in Chinese)
[19]楊彥宇.德國兩架警用直升機相撞墜毀[EB/OL]. (2013-03-21)[2014-12-12].http://www.chinanews.com/tp/hd2011/2013/03-21/186470.shtml.
YANG Yanyu. Two German police helicopters crashed collided[EB/OL]. (2013-03-21)[2014-12-12]. http://www.chinanews.com/tp/hd2011/2013/03-21/186470.shtml. (in Chinese)
[20]耿建華, 王霞, 謝鈞, 等. 通用航空概論[M]. 北京:航空工業(yè)出版社, 2007.
GENG Jianhua, WANG Xia, XIE Jun, et al. An introduction to general aviation[M]. Beijing: Aviation Industry Press, 2007. (in Chinese)
[21]江群, 王春. 民航基礎(chǔ)知識應(yīng)用[M]. 北京:國防工業(yè)出版社, 2011.
JIANG Qun,WANG Chun. Basics and application of civil aviation [M]. Beijing: National Defense Industry Press,2011. (in Chinese)
[22]朱金福. 航空運輸規(guī)劃[M]. 西安:西北工業(yè)大學(xué)出版社, 2008.
ZHU Jinfu. Planning of air transportation[M]. Xi’an: Northwestern Polytechnical University Press,2008. (in Chinese)
[23]廖瑛, 莊景釗, 梁加紅. 直升機工作特性建模與飛行性能仿真[J]. 國防科技大學(xué)學(xué)報, 2004, 26(5):5-8.
LIAO Ying, ZHUANG Jingzhao, LIANG Jiahong. The modeling of the working characteristics and simulation of the flying performance of helicopters[J]. Journal of National University of Defense Technology, 2004, 26(5):5-8. (in Chinese)
http://journal.nudt.edu.cn
Schedule of rescue helicopter departure time considering airway intersection
ZHANGJiaming1,LIUZhong1,SHIJianmai1,HEYunyue1,WANGYishan2,CHENChao1
(1. College of Information System and Management, National University of Defense Technology, Changsha 410073, China;
2. The PLA Unit 63796, Xichang 615000, China)
Abstract:Aiming at minimizing the departure time of the last helicopter, a mathematical programming model for multiple helicopters in multiple airports was set up to solve the departure time scheduling problem of multiple helicopters. A heuristic algorithm based on task priority was designed to solve the model, a scheme to deal with the airway intersection was put forward and an algorithm to solve the departure time was also established. Basing on the disaster rescue of the 6.8 magnitude earthquake in Yunnan Ludian, a departure time scheduling case which includes 24 helicopters in 12 airports was designed to validate the model and algorithms. The influence of airway intersection and the treatment measures were deeply discussed. The results demonstrate the efficiency of the model and algorithms in dealing with the scheduling problem of multiple helicopters.
Key words:disaster rescue; rescue helicopter; mission scheduling; airway intersection
中圖分類號:TP316
文獻標志碼:A
文章編號:1001-2486(2015)06-103-07
作者簡介:張家銘(1982—),男,云南曲靖人,博士研究生,E-mail:zjm08091018@163.com;劉忠(通信作者),男,教授,博士,博士生導(dǎo)師,E-mail:phillipliu@263.net
基金項目:國家自然科學(xué)基金資助項目(71201169,70771109,71471174)
收稿日期:*2015-01-07
doi:10.11887/j.cn.201506020

