基于稀疏貝葉斯學習的無源雷達高分辨成像

王天云于小飛陳衛東*丁 麗陳 暢

①（中國科學技術大學電磁空間信息重點實驗室 合肥 230027）

②（中國衛星海上測控部 江陰 214431）

基于稀疏貝葉斯學習的無源雷達高分辨成像

王天云①②于小飛①陳衛東*①丁 麗①陳 暢①

①（中國科學技術大學電磁空間信息重點實驗室 合肥 230027）

②（中國衛星海上測控部 江陰 214431）

針對無源雷達壓縮感知成像，該文提出一種基于稀疏貝葉斯學習的高分辨成像算法。基于一次快拍模式下的無源雷達回波模型，文中首先考慮目標散射系數的統計特性及其對微波頻率的依賴關系，將無源雷達成像轉化為MMV（Multiple M easurement Vector）聯合稀疏優化問題；然后對目標建立了級聯形式的稀疏先驗模型，并利用稀疏貝葉斯學習技術進行求解。相比之前基于目標確定性假設的稀疏恢復方法，所提算法更好地利用了目標的統計先驗信息，具有能夠自適應調整參數（目標模型參數和未知噪聲功率）和高分辨反演目標等優點。仿真結果驗證了該算法的有效性。

無源雷達；高分辨率成像；稀疏貝葉斯學習；聯合稀疏優化

1 引言

無源雷達是一種利用外輻射源發射電磁波信號對目標進行探測或成像的雙/多基地雷達，具有優越的“四抗”性能，一直是雷達界的研究熱點。隨著通信、導航等新興技術的發展，存在于空間中的電磁波信號種類越來越豐富，目前被證實可用的外輻射源包括調頻廣播（FM）［1］，數字地面電視（DVB-T）［2］，中國移動多媒體廣播（CMMB）［3］，全球導航衛星系統（GNSS）［4］等。

作為傳統雷達成像（SAR， ISAR）技術的有益補充，近年來無源雷達成像得到世界各國的普遍重視，已成為雷達成像的重要研究領域［512］-。其中，文獻［5］利用目標散射系數和接收回波的傅里葉變換關系，提出了極坐標形式下基于單頻信號的無源雷達逐點匹配成像方法。文獻［6］提出了一種基于單頻連續波的無源雷達成像時域算法，利用信號匹配矩陣和回波信號矩陣的Hadamard積在時間維求和實現目標聚焦，避免頻域的插值處理。文獻［7］從電磁場模型出發，提出了基于濾波反投影思想的多孔徑無源雷達成像方法，不需預先知道發射機位置或者波形信息。以上幾種方法致力于解決外輻射源帶寬較窄時的成像問題，通常需要較多數目的發射機或者接收機才能獲得較好的成像性能。文獻［8］開展了利用全球導航衛星系統（GNSS）為照射源、地面站接收的Space-Su rface SAR（SS-SAR）成像技術，雖然充分利用了帶寬信息，但是為了獲得方位維的高分辨，需要構造大的合成孔徑，因而成像時間較長。文獻［9］提出了P-ISAR成像方法，將無源探測結果利用ISAR技術實現目標聚焦，但實測結果表明P-ISAR得到的成像分辨率較低。

隨著人們對高分辨率雷達圖像的需求越來越迫切，上述以奈奎斯特采樣定理為基礎的雷達信號處理技術對數據采樣及處理速率的要求也越來越高。近年來，壓縮感知（Com pressive Sensing， CS）理論利用目標稀疏先驗信息，在遠低于奈奎斯特采樣速率情形下，只需少量觀測樣本即可重構原始信號，可以有效減少雷達數據量及節省信號帶寬，為一次快拍下的目標成像提供了可能［13］。目前CS已廣泛應用于SAR成像［14］、ISAR成像［15］、M IMO雷達成像［13］以及無源雷達成像［1012］-等領域。文獻［10］將正交匹配追蹤（OMP）方法應用于多發多收單頻連續波無源成像。文獻［11］基于相同的信號模型，提出了ESPRIT的高分辨率無源成像方法，但在快拍數較少或者SNR較低時成像效果往往較差。文獻［12］雖然在推導無源雷達稀疏成像模型時考慮了帶寬因素，但文中假定目標散射系數是確定未知，并未考慮目標RCS起伏特性。本文在已有研究［12］的基礎上，利用目標散射系數在不同頻率下的統計特性［16］，提出了基于Lap lace先驗的稀疏貝葉斯學習成像算法（Lap lace-SBL）。文中首先建立了一次快拍下的無源成像模型，隨后考慮散射系數的統計特性及其對微波頻率的依賴關系［16］，選取了級聯形式的目標稀疏先驗模型，再基于稀疏貝葉斯學習理論［17］將無源成像轉化為MMV聯合稀疏優化問題［18］的求解。與無源雷達CS成像已有的稀疏恢復方法［1012］-不同（針對SMV問題，基于確定性重構技術），Laplace-SBL引入了統計學習的思想，能夠獲得較好的成像效果。

2 信號模型

本文研究的無源雷達成像模型如圖1所示，假定外輻射源陣列、接收雷達陣列與成像區域位于同一平面內。以目標中心所在位置作為坐標原點，第i個外輻射源位置為（ri，θi），其中i=1，2，…，I， ri為第i個外輻射源到原點的距離，θi為第i個外輻射源與x軸正向的夾角。同理，第j個接收雷達位置為（rj，θj），這里j=1，2，…，J，另外目標任一散射點位置用極坐標（r，θ）表示。

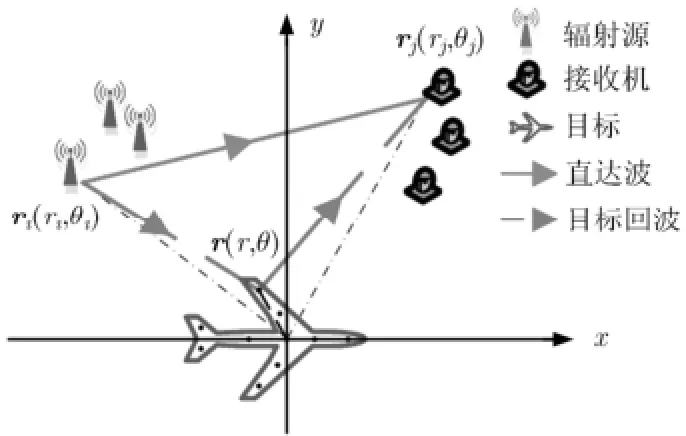
圖1 無源雷達2維成像構型

設外輻射源i發射信號為

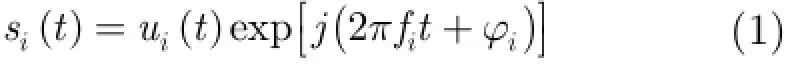
其中u（t）為信號復包絡，Bi為信號帶寬，fi為信號載頻，φi為初相。

無源雷達的接收機一般設置兩個接收天線，一個用來接收直達波，一個用來接收目標回波。接收機j獲取外輻射源i的直達波可以表示為

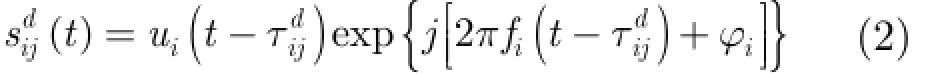
同理，接收機j收到外輻射源i對目標所有散射點的回波信號為

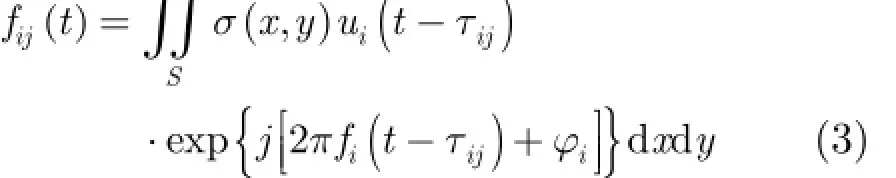
其中σ（x，y）為目標散射系數，τij=（rik+rkj）/c對應輻射源i發射的信號經散射點k反射后到達接收機j的總時延。rik表示輻射源i到散射點k的距離，rkj表示散射點k到接收機j的距離。

將直達波式（2）與目標回波式（3）分別去載頻之后，再對相應的基帶信號進行同步和混頻處理，可得

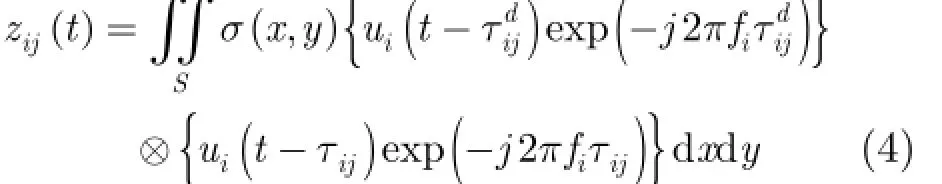
式中?表示復相關運算，對t進行傅里葉變換，并記Ui（f）=F｛ui（t ）｝， Zij（f）=F｛zij（t ）｝，式（4）轉化為

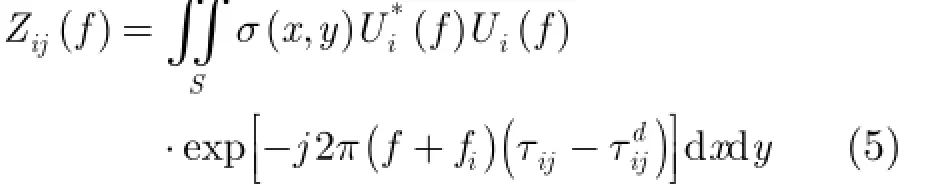
這里f∈（-Bi/2，Bi/2）。實際成像場景通常滿足遠場近似條件為

其中r=（r，θ）， Ii=ri/ri=（1，θi）， Ij=rj/rj=（1，θj）。

將式（6）代入式（5）經整理后得到

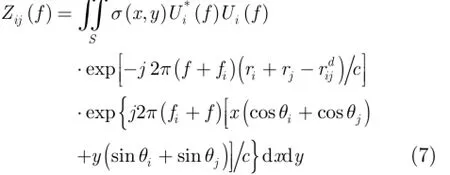
然后設計濾波因子：

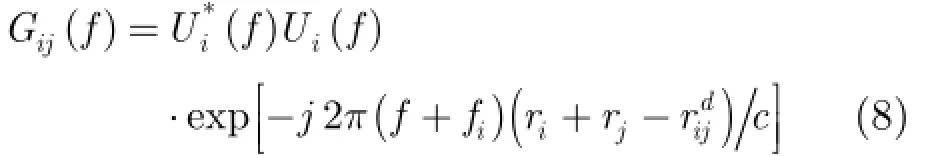
對式（7）進行頻域濾波，得到相應的回波方程為

定義空間譜［12］：

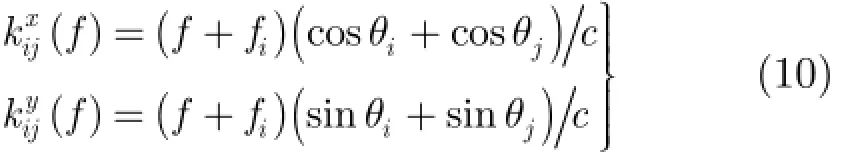
則發射機i和接收機j構成的接收通道對應的回波方程最終可寫為

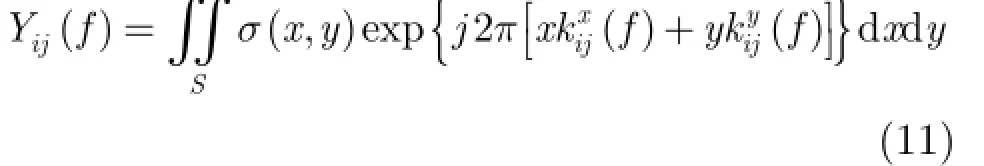
從式（11）可知目標散射系數與接收回波之間滿足傅里葉變換關系。由于增加了帶寬信息，式（11）是文獻［5，7，10］中回波方程的推廣。更進一步，本文拓展已有的研究［12］，考慮目標散射系數的統計特性及對微波頻率的依賴關系［16］，即σ（x，y）→σ（x，y，f）。因此第i，j個接收通道對應的回波方程應改寫為

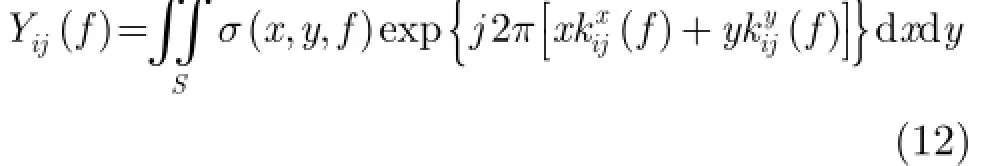
需要指出式（12）中f與fi密切相關。將式（12）作離散化處理，設每個收發通道的頻率采樣點數Fi相同，即Fi?F。由于常見的外輻射源信號帶寬往往較小，但不同發射機的載頻可以有較大變化。根據雷達目標特性理論，這里僅需考慮目標散射系數在不同發射機之間是變化的。其中發射機i對應的回波矢量為

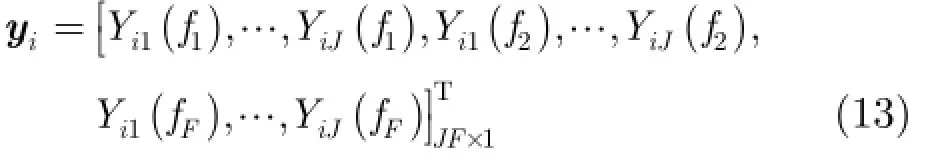
接著對成像場景進行網格劃分，尺度為U×V，則發射機i對應的目標散射系數矢量為

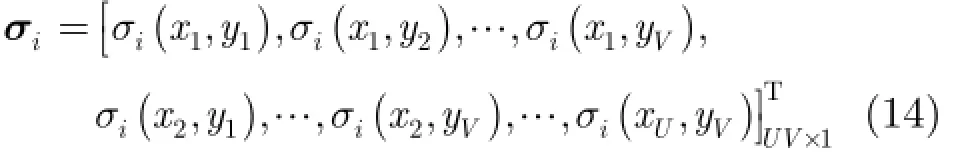
然后定義：

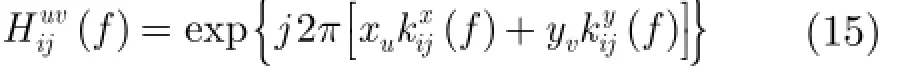
其中u=1，2，…，U， v=1，2，…，V ，構造發射機i對應的系統觀測矩陣為

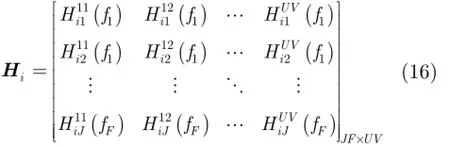
基于上述分析，一次快拍下的無源雷達回波方程式（12）最終應表示為其中ei為觀測噪聲。由于實際系統的限制（比如發射機位置和發射信號不可控，接收機數目不能太多等），目標散射系數在空間譜域的填充往往呈現出稀疏且非均勻的特點［12］，導致方程式（17）嚴重欠定，所以匹配濾波成像結果一般存在主瓣寬、旁瓣高、分辨率低等固有缺點［10］。考慮對空/海目標成像時，散射點在空間上通常滿足稀疏分布，因此可以引入CS成像技術獲得高分辨率圖像。結合式（17），σi中非零元素的位置對于不同的i是一致的，于是無源雷達CS成像最終等效為求解MMV聯合稀疏優化問題。與已有文獻中采用確定性稀疏恢復方法不同，本文提出了基于Laplace先驗的稀疏貝葉斯學習成像算法，不僅能夠提供σi的完整后驗概率密度函數估計，而且能同時獲得目標重構結果及噪聲功率等相關參數。具體過程見下節所示。

3 基于稀疏貝葉斯學習的無源雷達高分辨成像

3.1 目標參數稀疏貝葉斯模型

假設觀測噪聲矢量ei之間獨立，且服從復高斯分布CN（0，ηI）。其中η表示噪聲功率，為未知確定參數。則回波矢量｛yi｝ 的條件概率密度函數為

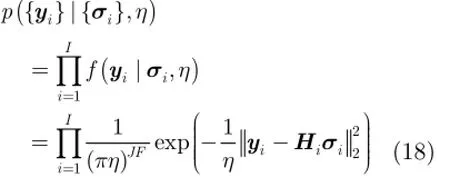
文獻［19］提供了一種級聯形式的稀疏貝葉斯先驗模型（如圖2所示），相比傳統稀疏先驗模型（如l1，lp范數約束），能得到對l0范數更好的近似度，具體描述如下：

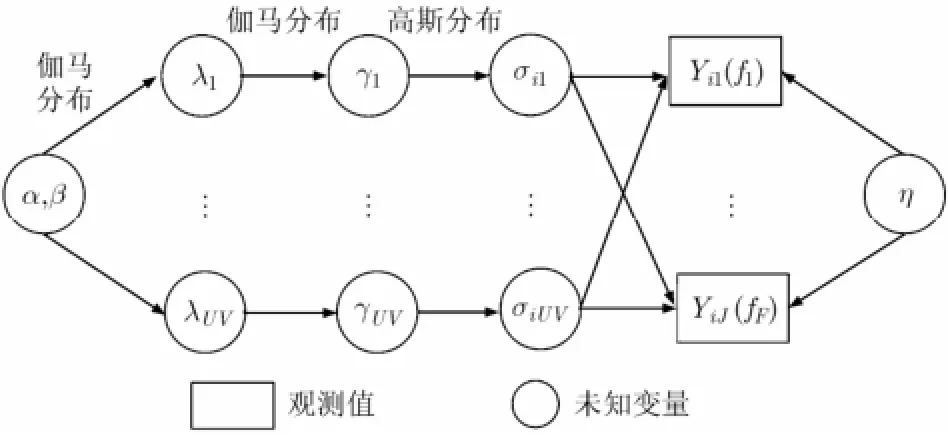
圖2 目標參數稀疏貝葉斯先驗模型

首先σi服從均值為零，方差為｛γ1，γ2，…，γUV｝的復高斯分布，定義Ψ=diag｛γ1，γ2，…，γUV｝，則有

其次｛γn｝服從伽馬（Gamm a）分布：

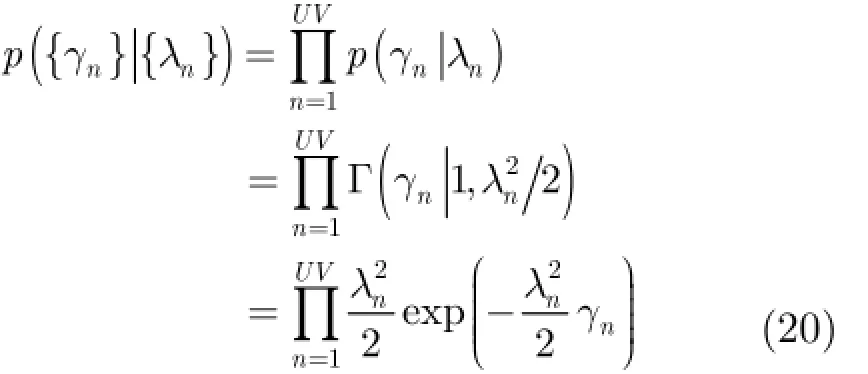
最后｛λn｝服從伽馬（Gamm a）分布：

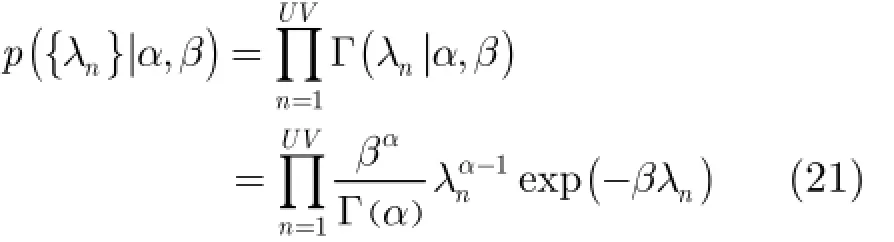
由式（19）及式（20）可以得到σi關于｛λn｝滿足拉普拉斯（Lap lace）分布，即

從式（22）可知，圖2對應的目標三級稀疏模型可以用式（22），式（21）兩級稀疏模型代替。因此在不影響目標稀疏重構性能的前提下，為進一步降低運算復雜度，本文選擇了后者用于下面成像算法的推導。

3.2 基于Lap lace先驗的稀疏貝葉斯學習（Laplace-SBL）成像算法

根據式（17），式（18），式（21）和式（22），目標散射系數矢量及噪聲功率等系統參數對應的聯合概率密度函數可表示為

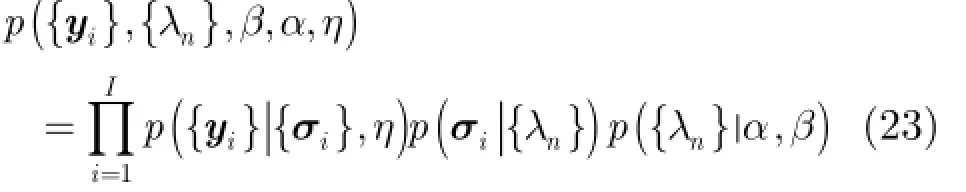
下面基于最大后驗（Maximum A Posteriori，MAP）準則求解聯合概率密度函數的最大值。通過對σi，λn，β，α，η交替迭代優化，最終實現無源雷達高分辨成像。由式（23）及MAP方法

令g=-lg p（｛yi｝，｛λn｝，α，β，η）。整理并略去常數項，式（24）對應的代價函數簡化為

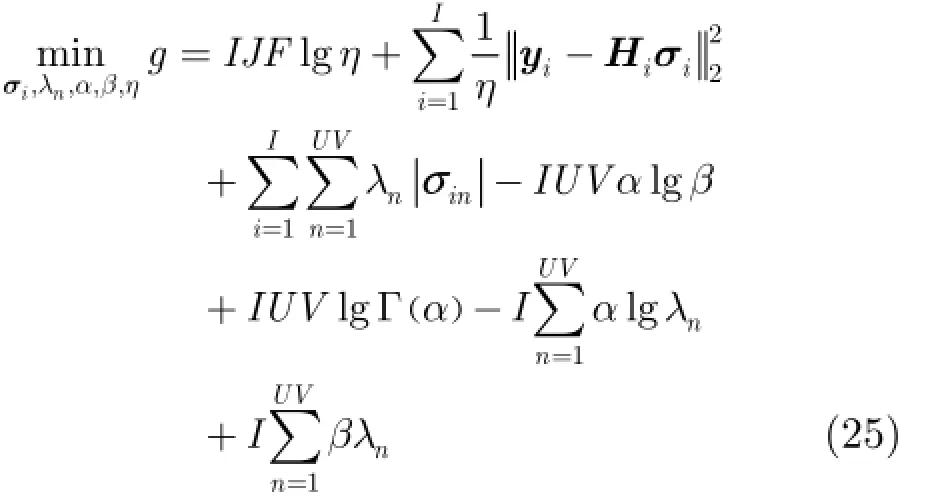
接著Laplace-SBL采用循環最小化（Cyclic M inim ization，CM）準則［18］迭代求解式（25），具體步驟如下：

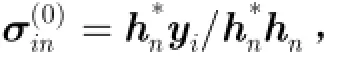
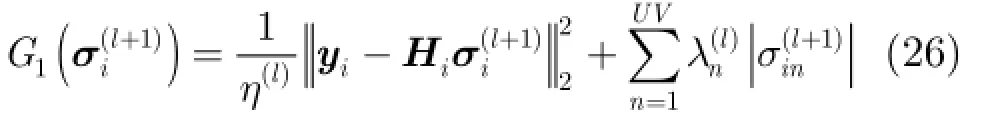
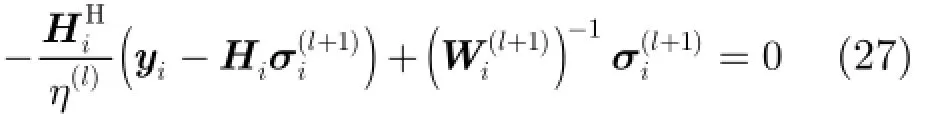
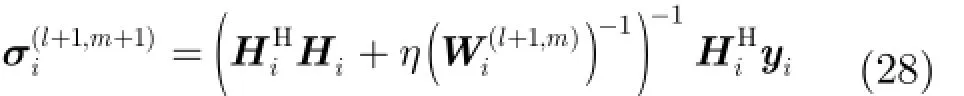
其中m為內部循環迭代次數，當m=0時，Wi（l，0）=Wi（l）。由于Ηi的行數遠小于列數，為降低計算復雜度，利用矩陣求逆引理重寫式（28）：

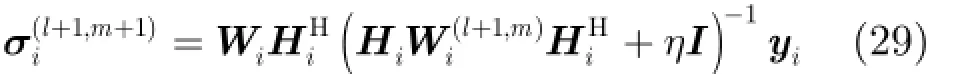
更進一步，可采用文獻［17］中的共軛梯度最小二乘算法加速式（29）的求逆運算，從而實現的快速收斂。

步驟3 固定其他參數，求解λn（l+1），其等價于最小化式（30）的代價函數：

令?G2/?λn=0可得

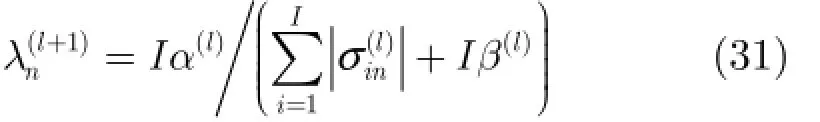
步驟4 固定其他參數，求解α（l+1），其等價于最小化式（32）的代價函數

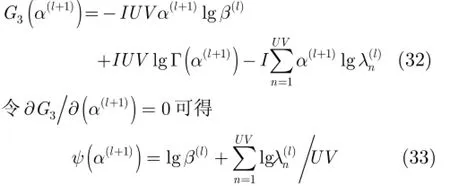
步驟5 固定其他參數，求解β（l+1），其等價于最小化式（34）的代價函數：

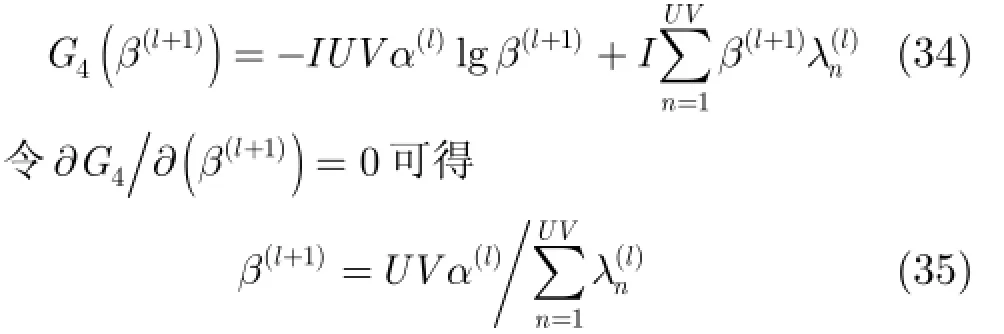
步驟6 固定其他參數，求解η（l+1），其等價于最小化式（36）的代價函數：

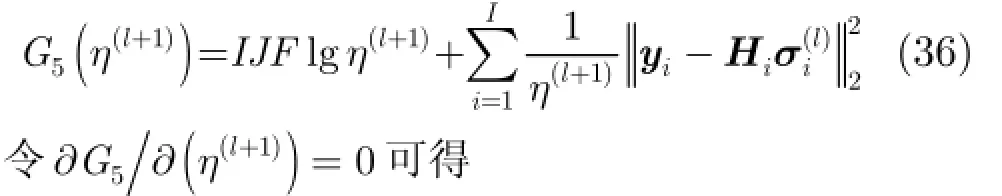
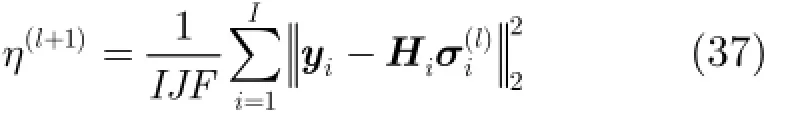
與文獻［18］類似，Laplace-SBL算法基于CM迭代求解，其代價函數g隨著迭代次數的增加是逐漸減小的。仿真表明當迭代次數達到15次時就能取得較好的成像結果。

3.3 與已有方法對比

已有的無源雷達成像方法主要分為兩大類，一類是基于奈奎斯特采樣定理的成像算法［5-9］，從本質上講可歸結于匹配濾波方法，在系統受限情形下獲取的目標空間分辨率較低；另一類是基于CS理論的高分辨成像算法［10-12］，之前的研究主要集中在確定性稀疏反演方法。本文提出了一種基于稀疏貝葉斯學習的高分辨成像方法，充分利用了目標的統計先驗信息，可以獲得穩健的成像結果。

注意到本文的回波模型式（17）與寬帶信號源的DOA估計相似，文獻［18］提出了兩種基于MAP準則的稀疏貝葉斯學習反演算法：W B-SLIM-0/1。通過對比各自的代價函數，可以看出Laplace-SBL是WB-SLIM-0/1的推廣。另外，在目標稀疏反演步驟，WB-SLIM-0/1是求解關于σ（l+1）的l范數優化問題；i2而根據式（26）可知，Laplace-SBL則是求解關于σ（l+1）的reweighted l范數優化問題，因而具有更好i1的稀疏重構效果［20］。

4 仿真結果與分析

下面通過仿真來驗證Laplace-SBL算法應用至無源雷達CS成像的有效性，并將成像結果和匹配濾波成像方法（MF）、傳統CS成像方法（FOCUSS［21］，BCS［19］， SLIM［17］）以及文獻［18］中兩種成像方法（WB-SLIM-0/1）進行對比，進而闡述本文算法的優越性。

本文仿真是針對對空或者對海目標（如飛機、導彈等）在一次快拍情形下進行的無源成像。假定無源雷達收發單元與目標成像區域位于同一平面，以成像場景中心為參考點，成像區域大小設為20 m× 20 m，對應的可分辨單元為1 m×0.5 m，故x維的網格數U=21， y維的網格數V=41。另外選取4個發射機和8個接收機（即I = 4， J = 8），它們與x軸的夾角可任意設置，文中θi∈（π/10， 2π/10， 5π/10，6π/10），θj在（90π/180， 150π/180）內均勻分布。這里選用文獻［3］中的CMMB基站作為外輻射源：信號帶寬為8 MHz，調制方式為OFDM。根據中國電視頻道劃分和頻率配置規定，4個發射機的中心頻率依次設定為fi∈（546 MHz，706 MHz，498 MHz， 474 MHz），另外每個收發通道的頻率采樣點數F=15，此時回波方程式（17）的行數遠小于列數，屬于欠定形式。

實驗1 不同信噪比情形下各方法的成像結果對比 假定原始成像目標由10個強散射點組成，且散射點均位于網格點上。另外設目標滿足Swerling I模型，其散射系數隨頻率發生變化且服從復高斯分布CN（0，1）［16］。為顯示方便，將各算法獲得的取平均作為成像結果，記為。類似地，為原始目標取平均的成像結果，如圖3（b）所示。圖3（c）～3（i）是SNR=20 dB時不同方法的成像對比。由圖可見，圖3（c） MF方法成像結果最差，這是因為MF基于Fourier重構技術，分辨率受限于空間譜填充大小（如圖3（a）所示，由于空間譜稀疏且不規則，導致MF具有較高的旁瓣和較寬的主瓣）。圖3（d）～3（f）是傳統CS方法的反演結果，由于它們沒有利用目標散射系數對頻率的依賴特性，反演結果中出現了較多的“虛像”。由3.3節可知，本文方法要優于WBSLIM-0/1，因此相比圖3（g）～3（h），圖3（i）獲得了更好的圖像重構效果。圖4和圖5分別是Lap lace-SBL的噪聲功率估計值?η以及代價函數隨迭代次數的變化關系，可以看出該方法具有較高的參數提取精度和較快的收斂速度。

實驗2 不同方法的成像誤差與SNR及稀疏度之間的關系 定義成像誤差為

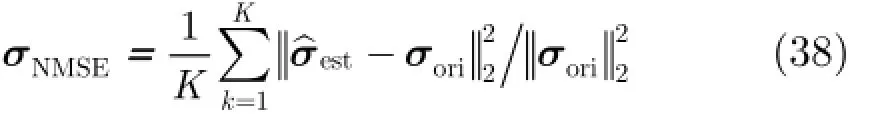
其中K為蒙特卡洛（Monte Carlo）實驗次數，文中設定K=30。為衡量不同稀疏重構方法的反演性能界限，這里增加OSR （Oracle Sparse Recovery）［22］算法，即預先精確已知目標散射點的位置，直接利用最小二乘方法求解散射系數。假設SNR從0 dB至25 dB變化，目標散射點模型與實驗1一致，圖6展示了不同方法的成像誤差隨SNR變化曲線圖。可見不同SNR下Laplace-SBL算法的成像誤差均低于其他稀疏反演方法，其成像性能隨著SNR增加逐漸逼近OSR，并在SNR＞5 dB時具有較好的成像效果。圖7為不同方法的成像誤差隨著稀疏度（散射點數目）變化的關系曲線，這里固定SNR=20 dB。由圖7可見，FOCUSS成像結果一直較差，與稀疏度的關系不大；其余方法則隨著稀疏度的增大，在迭代更新尋找散射點位置信息時出錯機率都有一定程度的增加，故成像誤差也隨之增大。但相比而言，Lap lace-SBL成像誤差最小，且限定在一定的范圍之內，從而驗證了該算法的有效性。

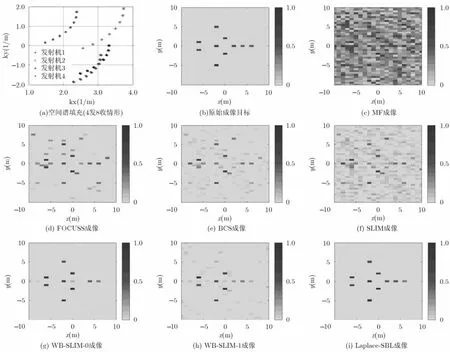
圖3 CMMB無源雷達空間譜填充及不同方法成像結果（SNR=20 dB）

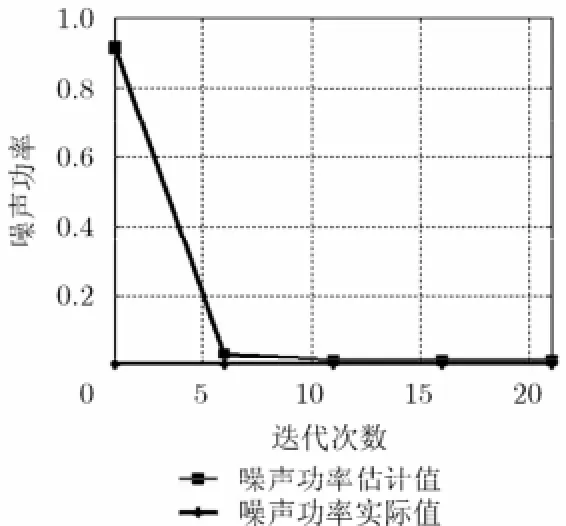
圖4 噪聲功率估計隨迭代次數變化關系（SNR=20 dB

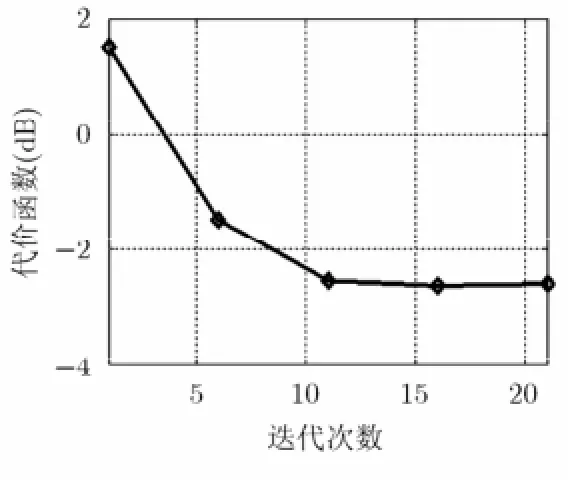
圖5 代價函數隨迭代次數 變化關系（SNR=20 dB）

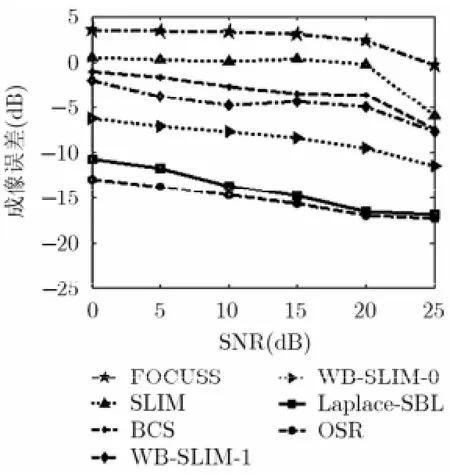
圖6 成像誤差隨S NR變化關系

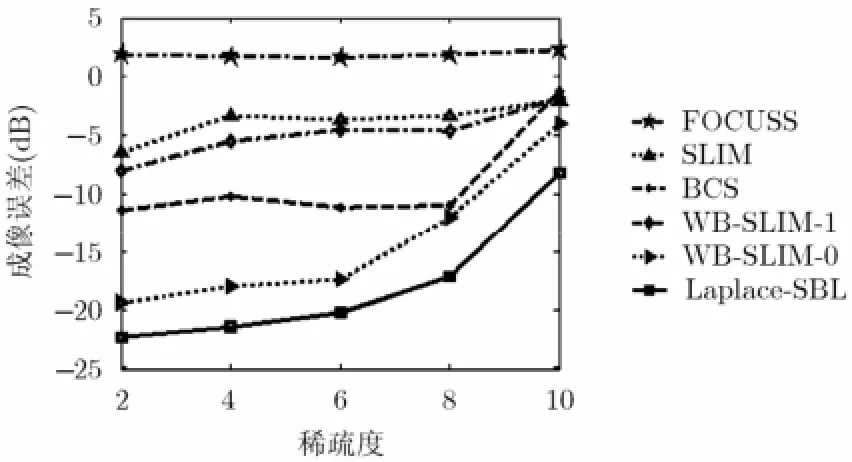
圖7 成像誤差隨稀疏度變化關系

5 結論

在已有研究［12］的基礎上，本文考慮了目標散射系數對微波頻率的依賴關系，將無源雷達CS成像轉換為求解MMV聯合稀疏優化問題，并提出一種基于稀疏貝葉斯學習的高分辨率成像算法，獲得了較好的成像效果。本文的信號建模方法及Laplace-SBL算法雖然以2維成像平面為例，但容易推廣至無源雷達3維成像。此外，文中所提的Laplace-SBL算法還可以應用至ISAR成像、M IMO成像等。

［1］ Liu Chang-chang and Chen Wei-dong. Sparse self-calibration imaging via iterative MAP in FM-based distributed passive radar［J］. IEEE Geoscience and Remote Sensing Letters， 2013， 10（3）: 538-542.

［2］ Palm er J E， Harms H A， Searle S J， et al.. DVB-T passive radar signal processing［J］. IEEE Transactions on Signal Processing， 2013， 61（8）: 2116-2126.

［3］ 萬顯榮， 岑博， 程豐， 等. 基于CMMB的外輻射源雷達信號模糊函數分析與處理［J］. 電子與信息學報， 2011， 33（10）: 2489-2493. W an X ian-rong， Cen Bo， Cheng Feng， et al.. Ambiguity function analysis and processing of CMM B signal based passive radar［J］. Journal of Electronics & Information Technology， 2011， 33（10）: 2489-2493.

［4］ Liu F， Antoniou M， Zeng Z， et al.. Coherent change detection using passive GNSS-based BSAR: experim ental proof of concepts［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2013， 51（8）: 4544-4555.

［5］ 王大海， 王俊. 單發多收模式下無源雷達成像研究［J］. 電子學報， 2006， 34（6）: 1138-1141. Wang Da-hai and Wang Jun. Research of passive radar imaging using single external illum inator and m ultip le receivers［J］. Acta Electronica Sinica， 2006， 34（6）: 1138-1141.

［6］ 劉玉春， 王俊， 楊杰， 等. 基于單頻連續波的無源雷達成像研究［J］. 電子與信息學報， 2013， 35（5）: 1108-1113. Liu Yu-chun， Wang Jun， Yang Jie， et al.. Research of passive radar imaging based on single-frequency continuous wave［J］. Journal of E lectronics & Inform ation Techno logy， 2013， 35（5）: 1108-1113.

［7］ Wang Ling， Yarman C E， and Yazici B. Doppler-hitchhiker: a novel passive synthetic aperture radar using ultranarrowband sources of opportunity［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2011， 49（10）: 3521-3537.

［8］ Antoniou M， Zeng Z， and Liu Fei-feng. Experimental dem onstration of passive BSAR im aging using navigation satellites and a fixed receiver［J］. IEEE Geoscience and Rem ote Sensing Letters， 2012， 9（3）: 477-481.

［9］ O livadese D， Giusti E， Petri D， et al.. Passive ISAR w ithDVB-T signals［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2013， 51（8）: 4508-4517.

［10］ 徐浩， 尹治平， 劉暢暢， 等. 基于壓縮感知的稀疏無源雷達成像［J］. 系統工程與電子技術， 2011， 33（12）: 2623-2630. Xu Hao， Yin Zhi-pin， Liu Chang-chang， et al.. Sparse passive radar imaging based on com pressive sensing［J］. System s Engineering and Electronics， 2011， 33（12）: 2623-2630.

［11］ 李巖， 王俊， 張守宏. 基于外輻射源的ESPRIT 超分辨成像算法［J］. 電子與信息學報， 2009， 31（1）: 143-146. Li Yan， W ang Jun， and Zhang Shou-hong. ESPR IT superresolution imaging algorithm based on external illum inators［J］. Journal of Electronics & Information Technology， 2009，31（1）: 143-146.

［12］ Wang Tian-yun， Liu Chang-chang， Lu Hong-chao， et al.. Sparse passive radar imaging based on digital video b roadcasting satellites using the M USIC algorithm［C］. Preceedings of the IEEE 11th International Conference on Signal Processing， Beijing， 2012: 1925-1930.

［13］ Wang Dang-wei， M a Xiao-yan， Chen A L， et al.. Highresolution im aging using a w ideband M IMO radar system w ith two distributed arrays［J］. IEEE Transactions on Im age Processing， 2010， 19（5）: 1280-1289.

［14］ Yang Jun-guang， Thom pson J， Huang Xiao-tao， et al.. Segmented reconstruction for com pressed sensing SAR imaging［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2013， 51（7）: 4214-4225.

［15］ Liu Hong-chao， Jiu Bo， Liu Hong-wei， et al.. Superresolution ISAR im aging based on sparse Bayesian learn ing［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（8）: 5005-5013.

［16］ Gorji A A， Tharmarasa R， and Kirubarajan T. Optimal antenna allocation in M IMO radars w ith collocated antennas［J］. IEEE Transactions on Aerospace and Electronic Systems，2014， 50（1）: 542-558.

［17］ Tan X， Roberts W， Li Jian， et al.. Sparse learning via iterative m inim ization w ith app lication to M IMO radar im aging［J］. IEEE Transactions on Signal Processing， 2011，59（3）: 1088-1101.

［18］ Xu Lu-zhou， Zhao Ke-xin， Li Jian， et al.. W ideband source localization using sparse learning via iterative m inim ization［J］. Signal Processing， 2013， 93（12）: 3504-3514.

［19］ Babacan S D， Molina R， and Katsaggelos A K. Bayesian com pressive sensing using Lap lace priors［J］. IEEE Transactions on Image Processing， 2010， 19（1）: 53-63.

［20］ W ipf D and Nagarajan S. Iterative reweighted l1and l2methods for finding sparse solutions［J］. IEEE Journal of Selected Topics in Signal Processing， 2010， 4（2）: 317-329.

［21］ Gorodnitsky I F and Rao B D. Sparse signal reconstruction from lim ited data using FOCUSS: a re-weighted m inimum norm algorithm［J］. IEEE Transactions on Signal Processing，1997， 45（3）: 600-616.

［22］ Yang Z， Zhang C， and Xie L. Robustly stable signal recovery in com p ressed sensing w ith structured matrix perturbation［J］. IEEE Transactions on Signal Processing， 2012， 60（9）: 4658-4671.

王天云： 男，1986年生，博士生，研究方向為分布式雷達成像、壓縮感知.

于小飛： 男，1988年生，碩士生，研究方向為無源雷達信號處理.

陳衛東： 男，1968年生，教授，博士生導師，研究方向為雷達系統理論與技術、微波與毫米波技術.

丁 麗： 女，1985年生，博士生，研究方向為M IMO雷達成像、壓縮感知.

陳 暢： 男，1979年生，講師，研究方向為微波與毫米波技術、無源雷達信號處理.

High-resolution Imaging of Passive Radar Based on Sparse Bayesian Learning

Wang Tian-yun①②Yu Xiao-fei①Chen Wei-dong①Ding Li①Chen Chang①①（Key Laboratory of Electromagnetic Space Information， University of Science and Technology of China， Hefei 230027， China）
②（China Satellite M aritim e Tracking and Contro l Departm en t， Jiangyin 214431， China）

This paper p resents a high-resolution imaging method based on Sparse Bayesian Learning （SBL） for passive radar com pressed sensing imaging. Under the one-snapshot echo model， the p roposed method firstly takes account of the frequency-dependent statistics of the target scattering centers， and changes passive radar imaging into a joint M ultip le M easurement Vector （MMV） sparse op tim ization problem. Further， a hierarchical Bayesian fram ework for sparsity-inducing priori of the target is established， then the MM V problem is efficiently solved by utilizing the SBL theory. Unlike the previous sparse recovery algorithms relying on the determ inistic assump tion of the target， the p roposed method makes a better use of the target p rior information， and has the advantages of adap tively estimating parameters （including the parameters in the priori model of the target， and the unknown noise power） as well as the high-resolution imaging， etc.. Simulation resu lts show the effectiveness of the proposed m ethod.

Passive radar； High-resolution im aging； Sparse Bayesian Learning （SBL）； Joint sparse op tim ization

TN 958.97

： A

：1009-5896（2015）05-1023-08

10.11999/JEIT140899

2014-07-09收到，2014-10-17改回

國家自然科學基金（6117255， 61401140）和國家863計劃項目（2012AA122903）資助課題

*通信作者：陳衛東 wdchen@uste.edu.cn