利用學生錯誤資源提高數學教學效益

◎福建省上杭縣明強中學 范景山

利用學生錯誤資源提高數學教學效益

◎福建省上杭縣明強中學 范景山

學生在掌握前人經驗、探求新知的過程中，難免會出現這樣或那樣的錯誤．而他們也正是在教師的精心指導下，在不斷的糾錯過程中漸漸成長、成熟，最終走向成功的．因此，作為數學教師，在自己平時的教學過程中要善于捕捉學生的錯誤信息，并把該信息當作一種教學資源，追根溯源，找出錯誤原因，及時地幫助學生從錯誤的漩渦中跳出來，開展有效的數學課堂教學．

學生錯誤資源；有效；數學課堂教學

眾所周知，人對事物的認識是一個循序漸進的過程，是一個從無知到有知，從知之不多到知之較多，從膚淺到深刻的不斷提升的過程.學生對知識的掌握也是同樣的道理.數學是研究現實世界的空間形式和數量關系的科學，抽象性、科學性和應用的廣泛性是數學的主要特點.學生的知識學習，就是掌握前人的經驗，把人類共同的精神財富變為自己的精神財富.數學學習的建構學說認為：“數學知識不能從一個人遷移到另一個人，一個人的數學知識必須基于個人對經驗的操作、交流，通過反省來主動建構.”然而，學生在掌握前人經驗、探求新知的過程中，難免會出現這樣或那樣的錯誤.而他們也正是在教師的精心指導下，在不斷的糾錯過程中漸漸成長、成熟，最終走向成功的.因此，作為教師，在自己平時的教學過程中如何捕捉學生的錯誤信息？如何把該信息當作一種教學資源，及時地幫助學生從錯誤的漩渦中跳出來，開展有效的課堂教學？都是非常值得我們關注與思考的問題.

一、實驗舉證，捕捉錯誤信息

學生對數學知識的錯誤認識和應用往往來自于對該知識的不求甚解，其結果必然與真理存在偏差.因此，要幫助學生找出這些偏差，關鍵要幫助他們理解概念、定義、定理及公式等的來龍去脈.

【案例1】高中數學必修4第113頁A組第4題：平面上三個力F1、F2、F3作用于一點且處于平衡狀態，F1=N，F1和F2的夾角為45°，求：（1）F3的大小；（2）F3與F1夾角的大小.

當學生出現這種錯誤時，教師要有耐心.首先，你可提問學生：“這種做法對嗎？如果對，請說出其依據是什么；如果錯，請說出其錯誤的原因.”這種提問的方式，可以充分調動學生的思維積極性，大大激發學生的學習熱情，學生就會主動地去的思考和觀察.

我們可以給學生做這樣一個實驗：將一個10克的砝碼掛在兩個相同的彈簧秤的秤鉤上，使兩彈簧秤之間的夾角為120°（它們與鉛直線的夾角均為60°），當砝碼處于平衡狀態時，讓學生們觀察，彈簧秤的指數是否均為5克？通過觀察，學生們發現彈簧秤的指數均為10克.

可見，實驗與觀察并舉是發現錯誤的一個直觀而有效的檢驗手段.

【案例2】學生在開始學習兩角差的余弦公式時，往往會記成cos（α-β）=cosα-cosβ.為了幫助學生發現此類錯誤，教師可通過設問的方式引導他們采用賦值檢驗法.如α=90°，β=45°時，等號左邊的值為，而右邊的值為.顯然，這時cos（α-β）=cosα-cosβ是不成立的.進而發現，自己已將公式記錯了.

【案例3】學生在開始學習等差數列｛an｝的性質時，往往會記成am+an=am+n（m，n∈N*）.為了幫助學生發現此類錯誤，教師可通過設問的方式引導他們也采用賦值法，即特值檢驗法.如對任意一個非零的常數列，將其代入檢驗后，上式均不成立.進而讓學生發現，自己已將公式記錯了.

二、追根溯源，找出錯誤原因

當學生發現錯誤后，作為教師，首先應該鼓勵他們：“你們已經進步了，因為正確的認識往往是從發現錯誤開始的.”

其次，教師再激勵學生：“當一個人認識錯誤后，更需要很好地改正錯誤，而要徹底地改正，又更需要找到犯錯的根本原因.你們說，是嗎？”學生們異口同聲：“是！”

師：“那么，案例1的第（1）小題中的錯誤解答F3=，到底錯在哪里？為什么不能像‘數的加法’一樣去做加法運算呢？”學生無言以對.

師：向量的定義是什么？

生：向量是既有大小又有方向的量.

師：數與向量有何區別？

生：數是只有大小的量.

師：因此，向量的加法能等同于數的加法嗎？

教師通過這樣的循循善誘，終于讓學生明白了剛才的錯誤所在.

分析發現，剛才的錯誤正是暴露了學生對“向量加法”的錯誤理解，其錯誤在于將“向量加法”與“數的加法”混為一談，其根源在于對“向量”的理解等同于對“數”的理解.

再看案例2中的錯誤cos（α-β）=cosα-cosβ和案例3中的錯誤am+an=am+n（m，n∈N*），通過分析也發現，學生沒有掌握公式的來龍去脈，進而無法對公式進行實質性的理解，導致對公式的記憶顯得膚淺毛糙、不求甚解，學習跟著感覺走.

三、探尋秘方，對癥下藥

當學生找到了錯誤根源后，教師應該趁熱打鐵，提出一些啟發性的問題，想辦法打開學生的思維大門，讓學生主動地去尋求解決問題的有效途徑.

再回過頭來看，案例1中F3=F1+F2=F1+F2的錯誤應改為

師：F1+F2=？

學生頓時恍然大悟，并爭相著回答：F1+F2=

可見，教師適時適度的啟發誘導是打開學生思維大門的催化劑.

接著，我繼續開展與學生互動的教學.

師：如果按原來的錯誤解法去做，那么題中的條件“向量F1和F2的夾角為45°”又有何意義呢？

聽了這一提問后，學生們對式子F1+F2=F1+ F2的錯誤有了更為深刻的認識.

師：向量的模的公式a=？，進而提出F3與F1、F2關系如何？

生：a=a2，且F1+F2=-F3.

師：如何利用這兩個等式去求F3呢？

聽了這樣的啟發之后，學生們頓時豁然開朗.

再看案例1中的第（2）小題？

師：如圖所示，設力F1和F3的夾角為θ，則.顯然，分母的值容易算，但分子的值又該如何去算呢？順著學生的這種錯誤思路，指出此法行不通.

生：那該怎么辦？

師：F1和F2的合力是F3′，它與力F3構成怎樣的關系？

生：互為相反向量.

師：換過一種思路，我們能否利用F3′與F1的夾角π-θ來考慮？cos（π-θ）=?

師：這樣看來，應該另尋一條出路.由于F1+F2=F3′，因此我們可以得到F2=F3′-F1，于是有F22=（F3′-F1）2，即

師再問：F3·′F1=？

生：F3′·F1=F3′·F1·co（sπ-θ）.

師：至此，同學們能求出θ了嗎？

生（異口同聲）：能！

作為教師，我們這時就應及時地對他們的回答給予積極鼓勵，讓他們真正體驗到“在快樂中學習，在學習中快樂”.

四、變式訓練，夯實知識根基

所謂數學變式訓練，即是指在數學教學過程中對概念、性質、定理、公式以及問題進行不同程度、不同層次、不同情形、不同背景的變式，以暴露問題的本質特征，揭示不同知識點間的內在聯系的一種教學設計方法.它是優化課堂教學的重要手段，在訓練中能有效改善學生的解題現狀，利用轉化發散學生思維，增強學生分析、解題能力.

比如，在掌握了案例1后，我們可進行下面的變式訓練：

變式1.已知F1=1，F2=2，F1和F2的夾角為60°，以F1和F2為鄰邊作平行四邊形，求此平行四邊形的兩條對角線中較短的一條的長度.

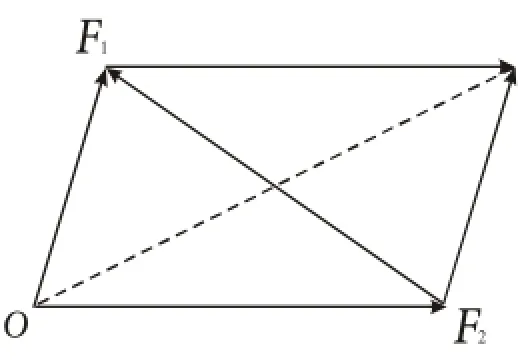
師：接下來又怎樣計算F2F1呢？

師：接下來，如何利用已知條件F1和F2的大小（即的大小）及其夾角60°計算呢？

觀察學生的神情，看似有點遺忘，教師因勢利導，再加以啟發.

通過這樣的一番啟發之后，學生們頓時豁然開朗，爭相著回答.這時，教師可以叫學生到黑板上板演.很快，學生就做出來了：

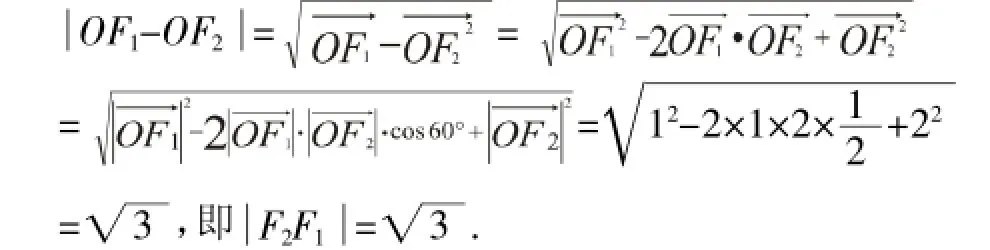
至此，問題得到了圓滿的解答.

下面就可以讓學生練習變式2與變式3.

經過以上變式訓練之后，教師可以幫助學生總結一下：“這些題目的解法有什么共同之處？均采用了什么公式？對我們今后的解題能帶來什么啟發與思考？”

五、反思錯誤，培養優良學習品質

古人云：“學而不思則罔.”這也就是人們常說的“鐵不用就會生銹，水不流就會發臭，人的智慧不用就會枯竭”.思考可以使人對知識理解得更深刻，思考可以使學的東西更扎實，未來社會最需要的就是善于思考、敢于創新的人.

而反思就是對自己經歷過的思想、心理感受及行為的體驗和思考，它是一種更能促進自身發展的思考.愛迪生說過，如果一個人在學習中有了反思的習慣，那么他必將是成功的學習者.

比如，在幫助學生解答完案例1時，教師可以采用反問的方式，總結一下學生所犯過的錯誤.

師：在案例1中，你們為什么會出現F1+F2=F1+ F2的錯誤呢？

師：那應該怎么用呢？

……

其實，教師巧妙的設問教學（尤其是反問）可以很好地培養學生“學會反思”這種優良的學習品質.

用心對待教育和教學，用心對待學生，我們就會把學生的錯誤當作一種可開發和利用的寶貴的教學資源.只有這樣，我們的教育和教學才會有效而生動，才會富有強大的感召力和永恒的生命力！

（責任編輯：王欽敏）