城市需水量預測方法比較

劉春成，曾 智，龐 穎，陸紅飛，白芳芳，高 峰

(1.中國農業科學院農田灌溉研究所,河南新鄉 453002；2.河南新鄉農業水土環境野外科學觀測試驗站,河南新鄉 453002；3.江西省水利規劃設計院,江西南昌 330000)

城市需水量預測方法比較

劉春成1，2，曾 智3，龐 穎1，2，陸紅飛1，2，白芳芳1，2，高 峰1，2

(1.中國農業科學院農田灌溉研究所,河南新鄉 453002；2.河南新鄉農業水土環境野外科學觀測試驗站,河南新鄉 453002；3.江西省水利規劃設計院,江西南昌 330000)

為了提高城市需水量預測的精度,基于北京市2000—2011年的實際用水量數據,對比分析了BP神經網絡預測模型、灰色GM(1,1)模型、非線性趨勢模型和灰色神經趨勢組合預測模型及其基于馬爾科夫修正的各單項模型需水量預測結果。結果表明：組合預測模型優于各單項模型,基于馬爾科夫修正的各模型優于各未修正預測模型。基于馬爾科夫修正的灰色神經趨勢組合預測模型預測精度最高、效果最好。

城市需水量；需水量預測；BP神經網絡；灰色模型；非線性趨勢模型；灰色神經趨勢組合預測模型；馬爾科夫修正模型；預測精度

進行城市需水量預測有助于合理分配和利用水資源。常用的城市需水量預測方法有回歸分析法、趨勢預測法、馬爾科夫法、BP神經網絡法、灰色模型法和時間序列模型法等。不同的預測方法,各有優缺點,精度有一定的差別。不同預測模型限制條件不同,故一種預測方法僅能利用部分信息,無法兼顧全部有用的信息。為了提高預測的準確性和可靠性,有必要綜合各種預測方法,以便利用盡可能多的有用信息。筆者分析各種預測方法,對一些預測方法進行組合,以期尋找較好的城市需水量預測方法。

1 材料與方法

1.1 數據來源

選取2001—2011年北京市的用水指標用水量(數據摘選自2001—2011年的《北京市水資源公報》)見表1。

表1 北京市2001—2011年實際用水量統計 億m3

1.2 模型簡介

a.BP神經網絡法。BP神經網絡具有自學習、自組織和非線性等獨特的特點[1],其學習過程包括信息正向傳遞和誤差反向傳播,是應用最廣泛的神經網絡算法之一。張雪飛等[2]研究發現,以任一精度,3層的前向BP神經網絡均可以逼近任意非線性函數,且不需要模型,只需構建輸入向量和目標輸出的網絡關系就可模擬預測目標值,故BP神經網絡預測城市需水量的預測是簡單且十分有效的。3層BP神經網絡結構見圖1。

圖1 3層BP神經網絡結構

b.灰色GM(1,1)模型法。灰色系統理論是基于灰色生成函數概念,以微分擬合為核心進行建模的。該理論模型簡單且所需樣本少,在諸多領域應用廣泛。城市用水量具有已知和不確定信息,屬于一個灰色系統[3]。基于時間序列特性,構建灰色模型用于預測城市需水量具有一定可行性。常用的灰色GM(1,1)模型建模流程[4]如下:

由模塊x(1)構成的微分方程為

式中:a為系統發展系數；b為內生控制變量。對式(1)進行離散化得到:

式中:Y為序列變量矩陣；X為1階累加函數矩陣；B為估計量矩陣。

利用最小二乘法對式(2)進行變換得:

c.趨勢預測法。趨勢預測法不考慮其他影響因素,直接建立過去用水量和未來用水量的聯系。諸多預測方法中,該法所需數據少、操作簡單。常采用的函數關系有線性、非線性和指數關系等,公式如下:

線性模型:

非線性模型:

指數模型:

式中:WD為預測年需水量；T為預測年份序號,T= 1,2,…；A、B、C、D均為模型參數。

d.灰色神經趨勢組合預測法。組合預測模型[5-6]是綜合不同單項預測模型的預測結果,用組合權系數進行加權平均而得到的預測模型。組合權系數的合理選擇是組合預測模型的最關鍵環節。已有研究多以相對或絕對誤差為組合權系數的優化準則[7],為此,本文以絕對誤差之和最小為準則,構建灰色神經趨勢的線性組合預測模型,即,

式中:XZ為組合預測值；t為預測時段數；x^Gt,x^Bt,x^Qt分別為灰色GM(1,1)模型、BP神經網絡模型和趨勢預測模型在第t個時段的預測值；lG,lB,lQ分別為灰色GM(1,1)模型、BP神經網絡模型和趨勢預測模型在第t個時段的組合權系數。

lG,lB,lQ可參考經驗公式[4]求得:

n

i=1

式中:lk為第k種模型組合權系數,且∑lk=1；~dii為預測時段內第i種預測模型的殘差平方和。

本文n=3,用lG,lB,lQ表示l1,l2,l3,可得:

式中:~dG、~dB、~dQ分別為預測時段內灰色GM(1,1)模型、BP神經網絡模型和趨勢預測模型的殘差平方和。

e.馬爾科夫鏈預測法。馬爾科夫鏈是基于馬爾科夫過程,由當前時刻狀態推求出下一時刻狀態概率分布,屬于特殊的隨機過程[8]。根據對鏈內已知馬爾科夫過程狀態、相互關系的研究,預測鏈的未來變化。其預測結果是取值范圍,可以用于修正隨機波動性較大的預測。馬爾科夫鏈模型如下:

其中P(1)為一步轉移矩陣:

式中:P0、Pt+1分別為初始時刻、t+1時刻的概率分布；pij為一步轉移概率(與初始時刻無關),是由狀態ai(tn時刻)經一步轉移到狀態aj(tn+1時刻)的概1(i,j=1,2,3…n；m為正整數)。

2 模型應用

2.1 基于BP神經網絡模型的應用

基于Matlab軟件,對北京市2000—2011年的實際用水量原始數據進行歸一化處理,初始權值隨機化賦予,同時取學習效率為0.6。經數次訓練對比,選用3層BP神經網絡結構為1-9-1,即用前1年的用水量預測第2年的需水量,隱含層神經元個數為9。選用tansig傳遞函數構建輸入層和輸出層之間的網絡關系,網絡連接的閾值和權值采用動量項進行修正,詳細算法步驟見文獻[9]。訓練精度設定為0.001,最大訓練步驟為10 000步,由仿真訓練求得預測值及其誤差,詳見表2。

表2 不同模型下北京市2000—2011年需水量預測值與實際值的比較

2.2 基于灰色GM(1，1)模型的應用

基于Matlab軟件,對北京市2000—2011年的實際用水量數據進行計算,算法步驟見文獻[10]。求得灰色GM(1,1)預測模型的系統發展系數a= 0.00310772,內生控制變量b=36.1244。則有:

由MATLAB軟件計算出需水量預測值和誤差,詳見表2。

2.3 基于趨勢預測模型-非線性模型的應用

基于EXCEL軟件,對北京市2000—2011年的實際用水量數據按照式(6)進行擬合,求出模型參數A、B、C、D,并代入式(6)得:WD=43.705-3.725T+ 0.4647T2-0.017 5T3,并進行需水量預測(2000年T取1,依次類推),結果見表2。

2.4基于灰色神經趨勢組合預測模型的應用

基于灰色GM(1,1)模型、BP神經網絡模型和非線性趨勢預測模型的預測值,計算其殘差平方和,按式(10)計算出組合權系數lG=0.302,lB=0.254, lQ=0.444,并代入式(8)計算灰色神經趨勢組合預測模型的預測值及誤差值,結果見表2。

2.5 基于馬爾科夫鏈修正的BP神經網絡預測模型的實例應用

算法同BP神經網絡預測模型,基于表2中BP神經網絡預測相對誤差,將馬爾科夫的狀態區域劃分為:①[-6%,-1%]；①(-1%,1%]；③(1%, 8%]；④(8%,11%],并基于此進行分類。根據狀態區域的劃分,一步轉移概率矩陣為

2.6 基于馬爾科夫鏈修正的灰色GM(1，1)預測模型的實例應用

算法同灰色GM(1,1)預測模型,基于表2中灰色GM(1,1)預測相對誤差,將馬爾科夫的狀態區域可劃分為:①[-8%,-2%]；①(-2%,0%]；③(0%,2%]；④(2%,3.6%]。并基于此進行分類。根據狀態區域的劃分,一步轉移概率矩陣為

將P(G1

M)代入式(11),可得到基于馬爾科夫鏈修正的灰色GM(1,1)預測模型的預測結果(表3)。

2.7 基于馬爾科夫鏈修正的非線性趨勢預測模型的實例應用

算法同非線性趨勢預測模型,基于表2中非線性趨勢預測模型中相對誤差,將馬爾科夫的狀態區域可劃分為:①[-3%,-1%]；①(-1%,1%]；③(1%,2%]；④(2%,5%]。并基于此進行分類。根據狀態區域的劃分,一步轉移概率矩陣為

表3 基于馬爾科夫鏈修正的4種模型對北京市2000—2011年需水量的預測

將P(fx1)代入式(11),可得到基于馬爾科夫鏈修正的非線性趨勢預測模型的預測結果(表3)。

2.8基于馬爾科夫鏈修正的灰色神經趨勢組合預測模型的實例應用

算法同灰色神經趨勢組合預測模型,基于表2中灰色神經趨勢組合預測相對誤差,將馬爾科夫的狀態區域可劃分為:①[-4%,-2%]；①(-2%, 0%]；③(0%,1.5%]；④(1.5%,3%]。并基于此進行分類。根據狀態區域的劃分,一步轉移概率矩陣為

將P(zh1)代入式(11),可得到基于馬爾科夫鏈修正的灰色神經趨勢組合預測模型的預測結果(表3)。

2.9 結果分析與精度檢驗

由表2、表3可知,組合模型預測精度高于單一模型預測；基于馬爾科夫修正的BP神經網絡模型、灰色GM(1,1)模型、非線性趨勢模型和灰色神經趨勢組合預測模型的預測精度均高于未修正的相應模型。為了評價組合預測模型和各修正預測模型的優劣,基于后驗差檢驗和殘差檢驗的方法進行進一步分析。

a.殘差檢驗。由表2、表3中各模型的修正誤差序列可知,BP神經網絡模型、灰色GM(1,1)模型、非線性趨勢模型和灰色神經趨勢組合預測模型的馬爾科夫修正相對誤差絕對值的最大值分別為5.62%、5.36%、3.45%、4.13%,其修正相對誤差絕對值的平均值分別為2.14%、2.01%、0.99%、0.96%,均小于5%,平均精度均大于95%。

可見,修正后各模型的擬合精度均較高,其中修正灰色神經趨勢組合預測模型的擬合精度最高,修正非線性趨勢預測模型次之,分別為99.04%和99.01%。

b.后驗差檢驗。后驗差比值c是殘差均方差S與數據均方差S0之比。即c=S/S0。

小誤差概率P=P{|e(k)-eˉ|＜0.6745S0},其中e(k)、eˉ分別為各修正模型殘差序列、均值。

基于后驗差比值c和小誤差概率P把預測等級[10]分為4級(好,合格,勉強合格,不合格),見表4。

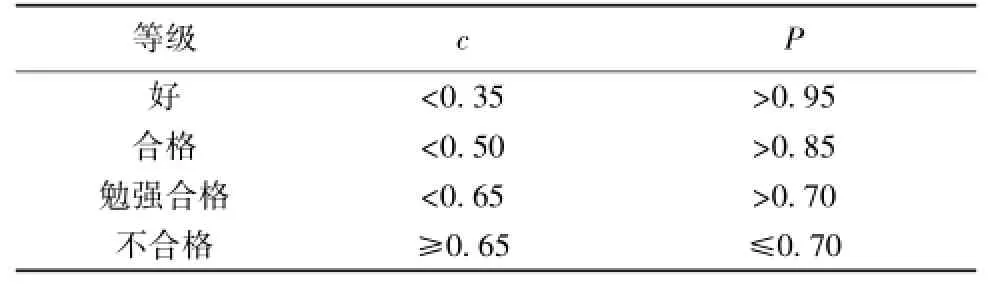
表4 檢驗指標標準

根據后驗差比值和小誤差概率公式得到基于馬爾科夫修正的BP神經網絡模型、灰色GM(1,1)模型、非線性趨勢模型和灰色神經趨勢組合預測模型的c值分別為0.584、0.430、0.286、0.272,P值分別為0.750、0.833、0.916、0.916。從表4可知,基于馬爾科夫修正的各種模型預測等級依次為勉強合格、勉強合格、合格、合格。

基于馬爾科夫修正的灰色神經趨勢組合預測模型的擬合精度高、穩定性好。根據該模型,2012年北京市預測需水量為35.28億m3,而北京市實際需水量為35.90億m3(來源于《2012年北京市水資源公報》),相對誤差為-1.73%。

3 結 論

基于北京市2000—2011年的實際用水量數據,對比分析了BP神經網絡預測模型、灰色GM(1,1)模型、非線性趨勢模型和灰色神經趨勢組合預測模型及其基于馬爾科夫修正的各單項模型的需水量預測結果,得出的主要結論為:基于馬爾科夫修正的灰色神經趨勢組合預測模型的擬合精度高、穩定性好,擬合效果優于灰色神經趨勢組合預測模型和其他馬爾科夫修正各單項預測模型。

但是,本文側重于模型方法應用分析,沒有結合當地的工農業發展規劃、居民生活用水情況、環境需水及節水措施等,相關工作有待進一步深入研究。

[1]胡文發.基于BP算法的國際工程項目政治風險評價模型[J].重慶建筑大學學報,2006,28(4):98-100.(HU Wenfa.BP algorithm evaluation model of political risking international construction projects[J].Journal of Chongqing Jianzhu University,2006,28(4):98-100.(in Chinese))

[2]張雪飛,郭秀銳,程水源,等.BP神經網絡法預測唐山需水量[J].安全與環境學報,2005,5(5):95-98. (ZHANG Xuefei,GUO Xiurui,CHENG Shuiyuan,et al. Prediction of urban water demand in Tangshan City with BP neutral network method[J].Journal of Safety and Environment,2005,5(5):95-98.(in Chinese))

[3]任煥蓮.基于灰色GM(1,1)模型的城市需水量預測研究[J].水利與建筑工程學報,2007,5(3):51-53.(REN Huanlian.Forecasting of urban water demand based on gray GM(1,1)model[J].Journal ofWater Resources and Architectural Engineering,2007,5(3):51-53.(in Chinese))

[4]張成才,崔雅博,胡彩虹.需水量預測方法研究[J].氣象與環境科學,2009,32(1):1-4.(ZHANG Chengcai, CUIYabo,HU Caihong.Study on water demand forecast methods[J].Journal of Meteorological and Environmental Sciences,2009,32(1):1-4.(in Chinese))

[5]BASTES JM,GRANGER C.The combination of forecasts [J].Operation Research Quarterly,1969,20(4):451-468.

[6]唐小我.組合預測計算方法研究[J].預測,1991,10 (4):35-39.(TANG Xiaowo.Study of computing method of combination forecasting[J].Journal of Forecasting, 1991,10(4):35-39.(in Chinese))

[7]周素霞,王明智,夏訓峰,等.最優組合預測模型在城市生活垃圾清運量中的應用[J].環境科學與技術,2010, 33(9):197-200.(ZHOU Suxia,WANG Mingzhi,XIA Xunfeng,et al.Application of optimal combination forecast model in forecasting delivering quantity of MSW in China [J].Journal of Environmental Science&Technology, 2010,33(9):197-200.(in Chinese))

[8]朱新國,張展羽,祝卓.基于改進型BP神經網絡馬爾科夫模型的區域需水量預測[J].水資源保護,2010,26 (2):28-31.(ZHU Xinguo,ZHANG Zhanyu,ZHU Zhuo. Prediction of water demand based on improved BP neural network and Markov model[J].Water Resources Protection,2010,26(2):28-31.(in Chinese))

[9]李學橋,馬莉.神經網絡-工程應用[M].重慶:重慶大學出版社,1996.

[10]馬溪原,王暖.基于MATLAB的灰色模型在城市月供水預測中的應用[J].市政技術,2008(4):368-369. (MA Xiyuan,WANG Nuan.Application of gray model in forecasting of city monthly water supply based on MATLAB language[J].Municipal Engineering Technology,2008(4):368-369.(in Chinese))

[11]寧宣熙.管理預測與決策方法[M].北京:科學出版社, 2003.

Com parison of urban water demand forecasting methods

LIU Chuncheng1,2,ZENG Zhi3,PANG Ying1,2,LU Hongfei1,2,BAI Fangfang1,2,GAO Feng1,2
(1.Farmland Irrigation Research Institute,Chinese Academy of Agricult ural Science,Xinxiang 453002,China；2.AgricultureWater and Soil Environmental Field Science Research Station of Xinxiang City Henan Province,Xinxiang 453002,China；3.Jiangxi ProvincialWater Conservancy Planning and Designing Institute,Nanchang 330000,China)

Based on the actual water demands of Beijing city from 2000 to 2011,the forecasting results of BP neural network model,grey GM(1,1)model,nonlinearmodel and grey-neural-trend forecasting model and their correspondingmodelmodified by Markov chain were contrasted and analyzed in order to improve the predicting precision of urban water demand.The results showed that the corresponding forecastingmodelwas better than single models,and modelsmodified by Markov chain were better than the unmodified models.In summary,grey-neuraltrend forecasting modelmodified by Markov chain has smaller errors and higher precision accuracy.

urban water demand；water demand forecasting；BP neural network；grey model；nonlinear trend model；grey-neural-trend forecastingmodel；forecasting precision

TV213.4

A

：1004 6933(2015)06 0179 05

10.3880/j.issn.1004 6933.2015.06.030

劉春成(1986—),男,助理研究員,碩士,主要從事農業水資源的利用與保護以及灌溉理論和技術方面的研究。E-mail: liuchuncheng986@sohu.com

2015 01 05 編輯:彭桃英)