部分區(qū)間刪失數據下指數分布中MLE的相合性

蔡定教，易景平

(1.北京師范大學 數學科學學院，北京 100875；2.安陽師范學院 數學與統(tǒng)計學院,河南 安陽 455000)

?

部分區(qū)間刪失數據下指數分布中MLE的相合性

蔡定教1，2，易景平2

(1.北京師范大學 數學科學學院，北京 100875；2.安陽師范學院 數學與統(tǒng)計學院,河南 安陽 455000)

[摘要]部分區(qū)間刪失數據包括精確數據以及區(qū)間刪失數據， 在慢性病研究中有廣泛的應用.本文主要考慮在具有1類部分刪失數據下指數分布中最大似然估計的相合性，在一定的正則條件下證明了最大似然估計的強相合性.

[關鍵詞]區(qū)間刪失;相合性;最大似然估計;緊集;生存函數

部分區(qū)間刪失數據在實際生活中有廣泛的應用. 如在慢性病的研究中，有些病人開始患病的年齡是已知的；而另一些人只知道現在已患病，因而只知道患病時刻在當前時刻之前；還有一類未患病的可疑個體，則只知患病時刻在當前時刻之后. 更一般的情形發(fā)生在跟蹤研究中，如亞類心絞病和冠心病的研究中. 對于一類病人，心絞病或冠心病的發(fā)病時刻是清楚的，但是對另一些病人則只在某兩個時刻進行臨床檢測. 此外在丹麥的糖尿病研究中的數據也是既有精確值也包含區(qū)間刪失數據.

我們知道在僅有精確值的情形，指數模型中未知參數的最大似然估計具有強相合性. 本文中我們考慮在具有1類部分區(qū)間刪失數據情形下最大似然估計的強相合性. 1類部分刪失數據具體描述如下：對于一些研究對象，我們能觀察到它們生存時間的精確值T1,…Tn1，然而對其他的對象卻只能知道它們的現狀. 也就是說對于這些組中的第j個對象，只知道它在檢測時刻Uj時是否已失效；因而觀測數據為：(δj,Uj),j=1,…,n2. 當未知失效時刻Tj≥Uj時δj=1；否則δj=0.

1生存分析模型

設生存分析模型服從參數為λ的指數分布. 則生存函數為S(x)=exp{-λx},x>0， 相應的密度函數為f(x)=λexp{-λx},x>0.

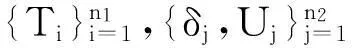
-exp{-λUj})(1-δj).

對數似然函數為：

+(1-δj)ln(1-exp{-λUj})].

假設1真值λ0為Λ的內點且Λ為緊集.

2Jessen不等式和Hoeffding不等式

Jessen不等式：設X為m維隨機向量，f為定義在Rm上的凸函數，EX存在有限，則

Ef(X)≥f(EX).

當f為嚴凸時，上式中等號當且僅當P(X=EX)=1時才成立.

Hoeffding不等式：設X1,…,Xn是個獨立隨機變量且P(Xi∈[a,b])=1,1≤i≤n,Sn=X1+…+Xn，則對任意t≥0，有

3相合性

定義1：對指數型分布族，最大似然估計MLE的定義如下：

這里p(x;λ)=(exp{-λUj})δ(1-exp{-λUj})(1-δ).令E為真實參數為λ0時的期望， 則對任意λ≠λ0，0<α<1，由Jessen不等式得

由p(x;λ)關于λ的可識別性知不等號嚴格成立， 即

(1)

對λ的任一領域N, 定義

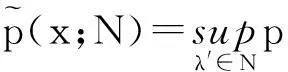
則對一列λ的半徑為ε的開領域Nε，當ε→0時， 有Nε收縮到λ， 從而有

由(1)式知當n1充分大而ε充分小時，存在ηε>0使得

(2)

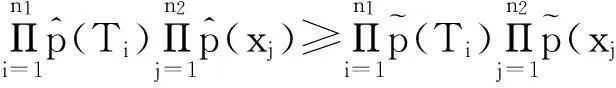
通過簡單的計算可得

再根據對數函數的凹性得

(3)

右邊和事件中每一項的概率為一致有界獨立隨機變量的平均值非負的概率. 而由(2)知這些隨機變量具有負的期望. 利用Hoeffding不等式，每一項的概率具有階e-εn2，這里ε取為2ρ2/(M-log(1-α))2, 其中M=max(ηλk,1≤K≤m)，ρ為某一負數且(2)中的期望n1>N在時小于ρ. 進一步有

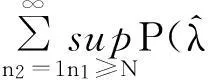
利用Borel-Cantelli引理及假設2知以概率1

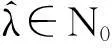
由N0的任意性即得證.

[參考文獻]

[1]Jong S. Kim. Maximum Likelihood estimation for the proportional hazards model with partly interval censored data [J].J.R.Statist.Soc.B,2003,65(2):489-502.

[2]Van der Vaart, A. W. and Wellner, J.A. Existence and consistency of maximum likelihood in upgraded mixture models[J].Multivariate Analysis,1992,43:133-146.

[3]Huang J. Efficient estimation for the proportional hazard model with interval censoring[J].The Annals of Statistics,1996,24(2):540-568.

[4]Huang J. and Wellner, J.A. Asymptotic Normal of the NPMLE of Linear Functionals for Interval Censored Data, Case 1[J]. Statistica Neerlandica,1995,49:153-163.

[5]Van der Vaart, A. W. and Wellner, J.A. Weak convergence and empirical processes[M]. New York：Springer Verlag, 1996.

[6]陳希孺.高等數理統(tǒng)計學[M].合肥:中國科學技術大學出版社,1999:192.

[責任編輯：Z]

[中圖分類號]O213.9

[文獻標識碼]A

[文章編號]1671-5330(2015)02-0006-02

[作者簡介]蔡定教(1979—)，男，浙江溫州人,北京師范大學博士生，講師，主要從事生物統(tǒng)計的研究。

[收稿日期]2015-02-02