變結構控制課堂教學中動力系統切換面設計
姚合軍
(安陽師范學院 數學與統計學院,河南 安陽 455000)
?
變結構控制課堂教學中動力系統切換面設計
姚合軍
(安陽師范學院 數學與統計學院,河南 安陽 455000)
[摘要]研究了相變量系統和多輸入多輸出動力系統切換面的六種設計方法。基于Hurwitz穩定性判據和等效控制、極點配置、最優控制、特征向量任置法,給出了多輸入多輸出動力系統的切換面設計方法,保證滑模面的穩定,為變結構控制器設計做好鋪墊。
[關鍵詞]變結構控制;切換面;動力系統
1引言
基于不連續控制率的變結構控制方法是處理系統魯棒穩定性的有效方法[1-4]。眾所周知,設計變結構控制器有兩個重要的環節: 1.設計合適的變結構控制器使得系統狀態在有限時間內到達并保持在切換面上。2.設計恰當的切換面和控制器保證被轉移到切換面上的點始終在切換面上運動,并漸近趨于原點。針對環節1,已有大量的研究結果報道,得到了各種各樣的趨近率保證系統狀態在有限時間內到達切換面。文獻[5]設計了帶有死區輸入的線性系統的變結構控制器[6]。Niu等人研究了針對一類具有非匹配不確定性和狀態及輸入時滯系統,設計了系統的變結構控制器。文獻[7]中,Xia等人研究了具有時變輸入和狀態時滯的線性系統的變結構控制問題。以線性矩陣不等式形式給出了切換面設計的時滯依賴的充分條件。Liu等人利用全局變結構控制方法研究了一類非線性系統的鎮定問題,得到了一個新的魯棒控制器,改進了系統的魯棒性和穩定性[8]。
然而控制器設計的前提是切換面的設計。近年來,有關于切換面設計的結果也有不少的報道。文獻[9]研究了一類多輸入多輸出系統的變結構控制問題,利用極點配置法設計切換面,并采用一種改進的指數趨近律,有效降低變結構所產生的抖振。在文獻[10]中,顏等人,針對一類離散不確定時滯系統,提出了一種輸出反饋變結構控制算法,基于LMI技術給出了切換面的設計方法。然而以往的研究結果對于切換面的選取并沒有統一有效的辦法,并且切換面的設計技巧性較強,對于初學變結構控制的學者來說不利于把握。正因為此,本文將給出不同系統的多種設計切換面的策略,在歸納總結前人研究的基礎上,針對相變量系統、多輸入多輸出系統,給出切換面設計的最優控制法,特征向量任置法等,為設計變結構控制打好基礎,為初學變結構控制的學者提供幫助。
2主要結果
(1)S>0


2.1 相變量系統的切換面設計
考慮下面n階相變量系統
(1)
其中ai(i=1,2,…,n),b均為常數。
選取切換面:
S=c1x1+c2x2+…+cn-1xn-1+xn
其中ci(i=1,2,…,n-1)滿足Hurwitz條件。
2.2 利用等效控制設計切換面
考慮下面正則型線性系統
(2)
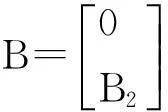
假設1:系統(2)可控,即(A,B)可控。
選取切換面:
S(t)=Cx(t)
(3)
其中C∈R(n-m)×n為待定的常數矩陣。
把(2)代入(3)式,并求導得到
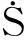
ueq(t)=-(CB)-1CAx(t)
把上式代入(2)中得到滑模方程
=[I-B(CB)-1C]Ax(t)
由上式知道可以設計系統的狀態反饋控制器,因此假設控制器為
u(t)=Kx(t)
(4)
其中K∈Em×n為待定的常數矩陣。
把(4)代入系統(2)得到
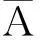
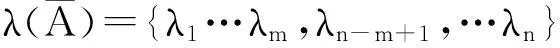
從而可以選取切換面系數矩陣C和矩陣W滿足

(5)
即可。
定理1對于滿足(5)的矩陣C和W,有CW=W
證明:在式子
兩邊同時左乘以矩陣C得到

從而CW=0。
2.3 利用二次型最優控制設計切換面
(6)
其中x(t)∈Rn為系統狀態,u(t)∈Rm為系統控制輸入,矩陣A∈Rn×n,B∈Rn×m為列滿秩常數矩陣。
選取系統二次型性能指標為:
J=∫0∞xT(t)Qx(t)dt
(7)
其中Q為半正定對稱矩陣。
對系統(6)作變換:
得到
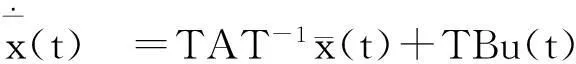

則滑動模態方程為
S(t)=0
其中切換面選為
(8)
其中C1是具有適當維數的矩陣。
由引理1得到



令
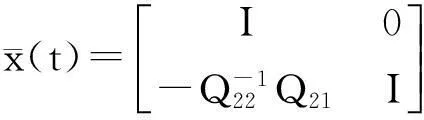
從而性能指標(7)變為
J=∫0∞xT(t)Qx(t)dt

對滑模方程
=A11x1(t)+A12x2(t)
由最優控制得到
2.4 利用極點配置方法選取切換面

選取切換面
(9)
其中C1,C2為具有適當維數的常數矩陣。
滑模方程為

其中C1可取任意非奇異矩陣,如單位矩陣。
令K=-C2-1C1可以確定C2,則滑動方程為:
S(t)=0
取新變量

則滑動方程為

從而
2.5 利用最優控制法設計切換面
對系統(6),選取性能指標為
J=∫0∞xT(t)Qx(t)dt
(10)
其中Q∈Rn×n為正定矩陣。
則
xT(t)Qx(t)
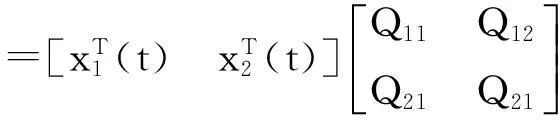


作變換
于是有

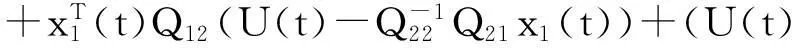
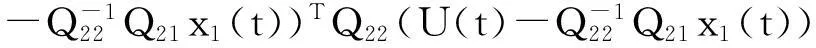
因此滑模方程
就變成了
這樣得到一個等價的性能指標
其解為
U(t)=Kx1(t)
其中P是滿足
的解。
2.6 利用特征向量任置法設計切換面
對系統(6)選取切換面為
S(t)=Cx(t)
其中C為具有適當維數的常數矩陣。
ueq(t)=-(CB)-1CAx(t)
代入系統(6)中得到
其中
K=(CB)-1CA
令S=Cx(t)=0得到滑動模態在C的零空間,即
ker(C)=N(C)
亦即
C(A-BK)x(t)=0?R(A-BK)?N(C)
記(A-BK)的特征根為λi(i=1,2,…,n),記λi的特征向量為νi(i=1,2,…,n),則有
C(A-BK)νi=0
亦即
Cλiνi=λiCνi=0
由此可知λi=0或νi∈ker(C)。
已知滑模是n-m維的,等價控制方程要成為滑模必有m個零根。假設n-m個特征根λ1,λ2,…,λn-m的特征向量ν1,ν2,…,νn-m張成ker(C),即
Span(v1,v2,…,vn-m)=ker(C)
于是有
CV=0
(11)
其中V=[v1V2…Vn-m]
由式(11)可解出矩陣C,但其解不唯一。
若將CV=0寫成

其中C1,C2為適當維數的矩陣,即
C1V1+C2V2=0
從而得到
C1=-C2V2V1-1
于是切換面的系數矩陣為C
3結論
本文是在前人研究的基礎上,針對相變量系統和多輸入多輸出動力系統,結合Hurwitz穩定性判據和等效控制、極點配置、最優控制、特征向量任置法,得到了多輸入多輸出動力系統的多種切換面設計方法,系統的歸納總結了切換面設計各種技巧,為變結構控制器的設計與實施做好鋪墊,為初學變結構控制的學者提供幫助。
[參考文獻]
[1]K.K. Shyu, W.J. Liu, K.C. Hsu. Design of large-scale time-delayed systems with dead-zone input via variable structure control[J]. Automatica, 2005, 41:1239-1246.
[2]X.K. Chen. Adaptive sliding mode control for discrete-time multip-input multip-output systems[J]. Automatica, 2006, 42:427-435.
[3]C.C. Hua, X.P. Guan, G. Duan. Variable structure adaptive fuzzy control for a class of nonlinear time-delay systems[J].Fuzzy Sets and Systems, 2004,148:453-468.
[4]S.W. Kau, Y.S. Liu, A new LMI condition for robust stability of discrete-time uncertain systems[J]. Syst. Contr. Lett.,2005.54:1195-1203.
[5]S.J. Bai, P.B, Q. Zhou, X. Huang. Variable structure controller design for linear systems with bounded inputs[J].International Journal of Control, Automation, and Systems, 2011, (2):228-236.
[6]Y. Niu, B. Chen, Sliding mode control for a class of nonlinear Ito stochastic systems with state and input delays[J]. International Journal of Control, Automation, and Systems, 2009,(7)33:365-370.
[7]Y. Xia, H. Yang, M. Fu, P. Shi, Sliding mode control for linear systems with time-varying input and state delays[J]. Circuits Syst Signal Process, 2011,30:629-641.
[8]L. Liu, Z. Han, W. Li, Global sliding mode control and application in chaotic systems, Nonlinear Dyn, 2009,56:193-198.
[9]于馳,宮明龍,多輸入多輸出系統的滑模控制器設計及其應用[J].東北大學學報(自然科學版),2012,33(4):473-475.
[10]顏閩秀,井元偉,何友國.一類離散不確定時滯系統的輸出反饋變結構控制[J].控制與決策,2009,24(4):499-507.
[責任編輯:Z]
Design of sliding mode surface for dynamical systems in variable structure control classroom teaching
YAO He-jun
(School of Mathematics and Statistics, Anyang Normal University,Anyang 455000,China)
Abstract:Six approaches have been given to design the sliding mode surface for dynamical systems in this paper. Based on the Hurwitz stability criterion、equivalent control、pole-placement method、optimum control、eigenvector method,several approaches have been obtained to design the stable sliding mode surface and the variable structure controller.
Key words:Sliding mode control; Discrete-time systems; Large-scale system with delays
[中圖分類號]TP273
[文獻標識碼]A
[文章編號]1671-5330(2015)02-0121-05
[作者簡介]姚合軍,男,副教授,主要從事動力系統方面的教學與研究。
[收稿日期]2015-01-29

