灰色Verhulst模型的初始值優化
王 健
(安陽師范學院 數學與統計學院,河南 安陽 455000)
?
灰色Verhulst模型的初始值優化
王健
(安陽師范學院 數學與統計學院,河南 安陽 455000)
[摘要]討論了一類灰色Verhulst模型的初始值優化問題.首先對模型的初始值增加擾動因素,然后通過最小化原始序列的一次累加序列與模擬序列之差,建立非約束優化模型,獲得了擾動因素的一個計算公式,并提出一種改進的灰色預測模型.最后,通過實例驗證了該改進模型可以有效提高預測精度.
[關鍵詞]灰色Verhulst模型; 擾動; 初值修正
1引言
灰色Verhulst模型[1,2]主要用來描述數據具有飽和狀態的過程,目前,該模型已經在國民經濟、社會發展等各個領域取得顯著應用[3,4]. 然而,有時模型的預測精度并不高,為此,很多學者進行了大量研究,通過優化參數估計、建立對應的離散模型、修改初始值以及改進灰導數等途徑,從不同方面對模型進行改進,并取得了良好效果[5-13]. 最近文獻[11]中提出了一種通過改進灰導數來提高模型預測精度的方法,即以白化微分方程為基礎,利用梯形公式來白化灰導數,使差分方程的參數與微分方程對應的參數有很好的一致性。
本文擬在上述研究基礎上,繼續討論Verhulst模型的初始值優化問題. 首先,利用文獻[11]中參數a,b的最優估計式,得到一種改進的灰色Verhulst模型. 同時,考慮對模型的初始值x(1)(n)增加擾動因素η,把x(1)(n)+η作為模型的新初始值,然后以原始序列的一次累加序列與一次累加序列的模擬值的殘差平方和最小為條件,建立一個無約束條件的優化模型,從而求出了擾動因素η,最后,通過一個計算實例,表明改進模型可以有效提高精度,具有較高的理論和應用價值.
2傳統灰色Verhulst模型
定義1[1,2]設X(0)為非負原始序列,
X(1)為X(0)的1-AGO序列,
Z(1)為X(1)的緊鄰均值生成序列,
其中,
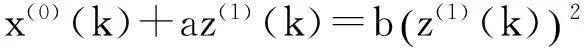
定理1[1,2]設X(0)為非負原始序列,X(1)為X(0)的1-AGO序列,Z(1)為X(1)的緊鄰均值生成序列,
其中,

(2)灰色Verhulst模型的時間響應序列為
(3)還原值
2灰色Verhulst模型的改進
最近,文獻[11]通過梯形公式改進了灰導數,優化了灰色Verhulst模型;并且給出了模型中參數a,b的最優估計式:

(1)
下面,我們以文獻[11]提供的模型為基礎著重討論初始值的優化問題.
眾所周知,傳統灰色Verhulst模型通常把x(1)(1)=x(0)(1)作為模型的初始值,這樣做是為了計算簡單,但缺乏科學性. 為此,文獻[9]根據灰色系統的新信息原則[1,2],提出了以X(1)的第n個分量x(1)(n)作為初始值,對Verhulst模型進行改進,并且給出了以新信息x(1)(n)為初始值的時間響應序列
(2)
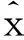
(3)
為求出擾動因素η,我們建立如下無條件優化模型
亦即
(4)
因此,優化問題(4)可轉化為如下情形:
(5)
定義指標函數

為簡單計,引入符號
則上式可寫成

-abR+aQ]
亦即
從而可得到一個關于擾動因素η的簡單而有效的計算公式
(6)
利用參數a,b的最優估計式(7)以及初始值修正為x(1)(n)+η和(6)式,我們得到如下改進的灰色Verhulst模型.
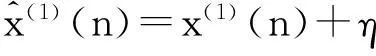
(2)灰色Verhulst模型的時間響應序列為


(3)還原值
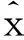
3實例驗證
現以2000-2008年我國高速公路事故死亡人數的變化實測數據為例,建立改進模型,并與傳統灰色Verhulst模型進行比較.
選用表1中前6個數據X(0)={2162,3147,3927,5269,6235,6407}建立模型,后3個數據用于模型的檢驗.

表1 全國高速公路2000-2008年事故死亡人數統計表(人)
3.1 傳統灰色Verhulst模型

于是,傳統灰色Verhulst模型的時間函數響應式為
k=0, 1, 2, ……
3.2 改進的灰色Verhulst模型
改進模型的建立優化和預測過程如下:
1)通過原始序列X(0),計算得到累加生成序列X(1)和緊鄰均值生成序列Z(1);
2)利用上述數據序列,分別求得

的結果;
3)根據定理2中(1)式,計算模型參數值a,b;
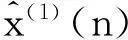
6)計算模擬誤差,并進行精度檢驗.
為便于比較,現將傳統灰色Verhulst模型、改進的灰色Verhulst模型在三步之內的預測值及平均誤差列表如下:

表2 兩種不同模型預測結果及相對誤差比較
從表2可以看出,傳統Verhulst模型在三步之內的平均預測誤差竟達12.4%,而改進模型的誤差只有8.01%,遠低于傳統Verhulst模型的平均相對誤,有較好的預測效果. 同時,文中所提供的擾動因素η的計算簡單、有效,也彌補了以往研究Verhulst模型時,文獻中沒有擾動因素η計算公式的不足.
4結論
本文基于新信息原理,對模型的初始值增加擾動因素η,即把x(1)(n)+η作為新的初始值;然后通過最小化原始序列的一次累加序列與模擬序列之差,建立非約束優化模型,并得到一個擾動因素η的計算公式. 實例表明,改進模型可以有效提高模型精度,從而拓廣了模型的使用范圍.
[參考文獻]
[1]鄧聚龍.灰色系統理論教程[M].武漢:華中理工大學出版社,1990.
[2]劉思峰,黨耀國,方志耕.灰色系統理論及其應用[M].北京:科學出版社,2004.
[3]羅戰友,龔曉南,楊曉軍.全過程沉降量的灰色verhulst預測方法[J].水利學報,2003,(3):29-31.
[4]慶衛,宋保維,賈躍.魚雷研制費用的灰色Verhulst模型[J].系統仿真學報,2005,17(2): 257-258.
[5]何文章,吳愛弟.估計Verhulst模型中參數的線性規劃方法及應用[[J].系統工程理論與實踐,2006,26(8): 141-144.
[6]王晗中,楊江平,黃美榮,劉飛.一種改進不等間距灰色預測模型[J].空軍工程大學學報, 2010,11(6):75-79.
[7]崔立志,劉思峰,李致平.灰色離散Verhulst模型[J].系統工程與電子技術,2011,33(3): 590-593.
[8]王豐效.基于初值修正的非等距灰色預測模型[J].重慶師范大學學報(自然科學版), 2006,23(3): 42-44.
[9]黨耀國,劉思峰,劉斌.以x(1)(n)為初始條件的GM模型[J].中國管理科學,2005,13(1): 132-135.
[10]王義鬧,劉開第.優化灰導數白化值的GM(1,1)建模法[[J].系統工程理論與實踐, 2001,21(5): 124-128.
[11]王正新,黨耀國,沈春光.灰色Verhulst模型的灰導數改進研究[J].統計與信息論壇,2010,25(6): 19-22.
[12]李玻,魏勇.優化灰導數后的新GM(1, 1)模型[J].系統工程理論與實踐, 2009,29(2):100-105.
[13]陳露,張凌霜.基于初值修正的組合灰色Verhulst模型[J].數學的實踐與認識,2010,40(11): 160-164.
[責任編輯:Z]
Study on Optimizing the initial Value of Grey Verhualst Model
WANG Jian
( School of Mathematics and statistics, Anyang Normal University, Anyang 455000, China )
Abstract:This paper discusses the optimizing initial value of grey Verhulst model, by adding the disturbing factors into the initial value of the model, and minimizing the differences between the 1-AGO sequence and simulation sequence of raw sequence and building an unconstrained programming model. It obtains a formula of disturbing factors, an amendatory grey Verhulst model was proposed in the paper. By comparison and analysis of some examples that amendatory model can have higher precision practicability and reliability
Key words:grey Verhulst model; disturbing factors ; modified initial value
[中圖分類號]N914.4; F224.9
[文獻標識碼]A
[文章編號]1671-5330(2015)02-0001-05
[作者簡介]王健(1972-),男,河南安陽人,安陽師范學院副教授,主要從事灰色系統理論研究。
[基金項目]河南省自然科學 (0511013800)
[收稿日期]2015-01-20

