基于滑模變結構的無線傳感器網絡擁塞控制

陳 樹,王夫棟

(江南大學物聯網工程學院,江蘇無錫214122)

基于滑模變結構的無線傳感器網絡擁塞控制

陳 樹,王夫棟

(江南大學物聯網工程學院,江蘇無錫214122)

為解決無線傳感器網絡逐跳節點擁塞控制問題,在節點網絡層與鏈路層之間引入水槽流入與流出的數學模型,提出一種針對逐跳節點級鏈路層幀緩沖區隊列長度的擁塞控制模型,并采用基于趨近律的離散滑模控制結構作為該模型的控制器,控制過程簡便且易于實現。仿真結果表明,與常規的PID控制、模糊PID控制相比,該模型在響應速度、延遲時間等方面性能較好。

無線傳感器網絡;擁塞控制;離散滑模控制;趨近律;滑模變結構

1 概述

無線傳感器網絡(Wireless Sensor Network, WSN)是一種無基礎設施的網絡,由傳感器節點以自組織形式構成,實現信號感知、數據采集和傳輸。由于無線傳感器網絡節點分布密集、信道鏈路的競爭和資源受限等特性,使得無線傳感器網絡容易出現擁塞,嚴重影響網絡的服務質量和生命周期,因此擁塞控制成為無線傳感器網絡的關鍵技術之一。無線傳感器網絡擁塞可以分為多個層次,其中之一就是節點級的擁塞,即節點需要發送的分組流量超過節點的發送能力,導致緩存溢出造成數據分組的丟失和網絡排隊延遲的增加［1-2］。

近年來,研究人員針對傳感器網絡應用及通信方式的特殊性提出了一些相關的解決節點擁塞的辦法。文獻［3-4］提出了基于緩沖區或信道使用情況的擁塞控制方法;文獻［5］利用基于隊列和信道估計預測的擁塞算法,并通過自適應流量控制算法調整速率;文獻［6］提出通過構造一棵最短路徑且是最小擁塞權值樹來解決擁塞現象,上述文獻大都基于WSN擁塞閉環控制。

本文受文獻［7］中提出的自動控制系統在水槽液位中的應用,以及文獻［8］中擁塞控制算法應用的啟發,提出一種針對逐跳節點級鏈路層緩沖區隊列長度的擁塞控制模型。該模型控制器采用基于趨近律的離散滑模控制結構,把單容水槽和雙容水槽流入與流出平衡關系應用到無線傳感器網絡擁塞控制當中。水槽水位控制與無線傳感器網絡擁塞控制雖

然控制領域和處理對象不同,但水槽液位控制與WSN的擁塞控制中的幀緩沖區長度控制有高度相似性,兩者都是保持流入與流出的平衡,把水槽的高度比作節點級鏈路層緩沖區隊列長度,從而得到新的擁塞控制模型。

2 離散時間系統滑模控制

考慮到無線傳感器網絡系統的復雜性、時變性及不確定性,將滑模控制引入到無線傳感器網絡的擁塞控制中。由于滑動模態可以進行設計且與對象參數及擾動無關,變結構控制具有快速響應、對參數變化及擾動不靈敏、物理實現簡單等優點,適合于無線傳感器網絡系統的應用研究。本文采用滑模變結構的方法來解決WSN擁塞問題。

根據文獻［9］,離散滑模面設計為:

其中,C=［c1c2…cn1］T,在滑模控制中,參數c1,c2,…,cn應滿足多項式pn-1+cn-1pn-2+...+c2p+c1為霍爾維茲,其中,p為Laplace算子。當系統為一階時,c=0;本文是二階系統設計,所以n=2,多項式pn-1+cn-1pn-2+…+c2p+c1變為p+c1,如果此式子是霍爾維茲,則多項式p+c1的特征值實部分為負,即c1＞0。理想誤差e(k)=xd-x(k),xd為理想輸出,由此可得:

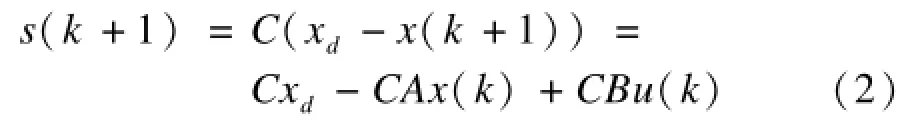
根據文獻［11］可知,基于指數趨近律的式子為:

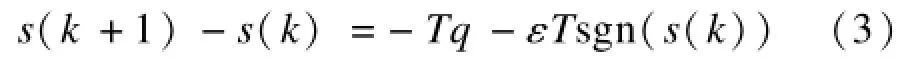
將式(2)代入趨近律式(3)得:

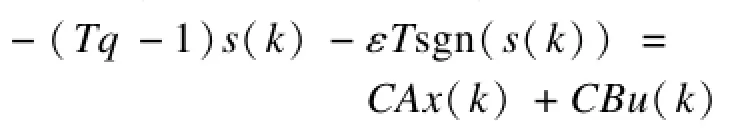
假設滑模變結構可控條件CB≠0成立,離散滑模控制律為:

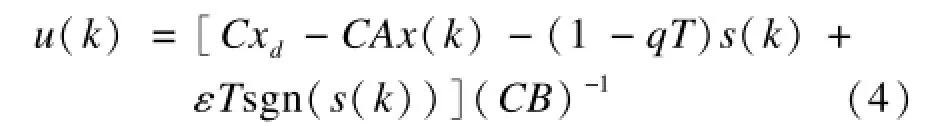
為避免控制器抖振,采用飽和函數sat(s)替換理想滑動模態中的符號函數sgn(s):

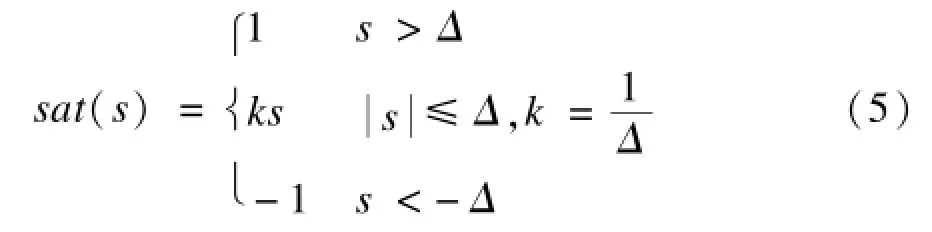
則控制律式變為:

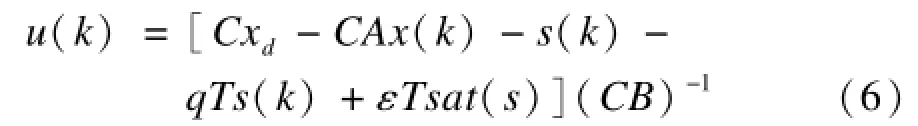
由于基于指數的離散趨近律式滿足［10］:

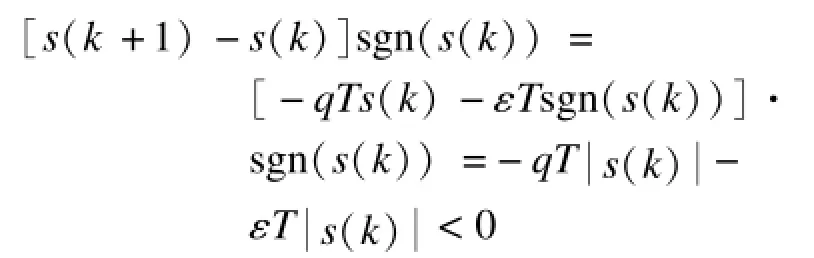
同時,當采樣時間T很小時,2-qT＞＞0,有:

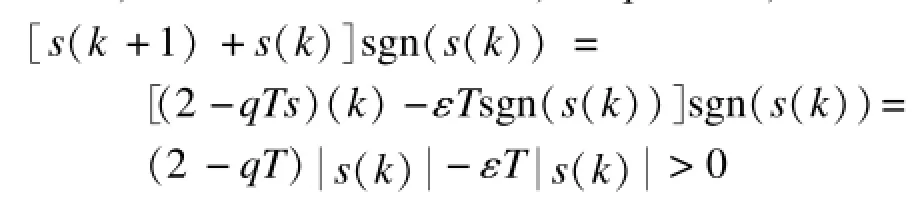
所以,離散趨近律式滿足到達條件,可保證趨近律模態具有良好的品質,并且切換帶的大小可以計算,求解滑模動態控制直接而簡單。

3 擁塞控制模型設計

3.1 單個節點擁塞控制模型

參照文獻［7］中的單容水槽控制模型,如圖1所示,設計單節點緩沖區控制模型,如圖2所示。

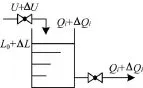
圖1 單容水槽

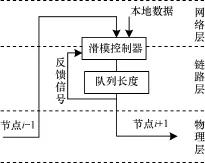
圖2 單節點模型

令U表示輸入數據包速率的穩態值,ΔU表示輸入數據包速率的增量,Q0表示輸出數據包速率的穩態值,ΔQ表示輸出數據包速率的增量,L表示節點緩存區的隊列長度,L0表示節點緩存區隊列長度的穩態值,ΔL表示節點緩存區的隊列長度的增量。

流出的數據包與流入數據包之差為:

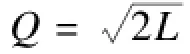
將上式帶入式(7)得:

其中,T=RA。在零初始條件下,對式(9)進行拉氏變換,得到單個節點的傳遞函數為:

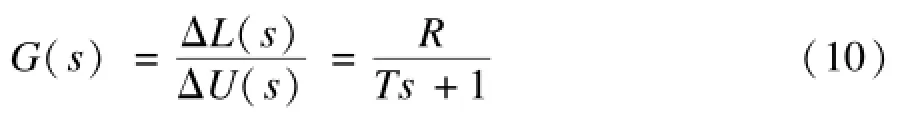
3.2 多節點擁塞控制模型

參照文獻［7］雙容水槽控制模型,如圖3所示,設計2個節點傳輸模型,如圖4所示。

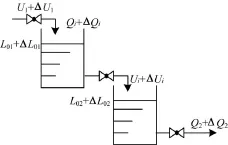
圖3 多容水槽

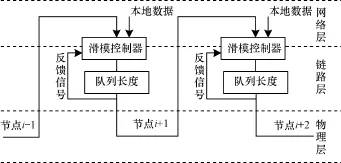
圖4 多節點模型

令u1表示第1個節點輸入數據包速率的穩態值,Δu1表示輸入數據包速率的增量,Q1表示輸出數據包速率的穩態值,ΔQ1表示輸出數據包速率的增量,L1表示節點緩存區的隊列長度,L01表示節點緩存區隊列長度的穩態值,ΔL01表示節點緩存區的隊列長度的增量。令Q2表示第2個節點輸出數據包速率的穩態值,ΔQ2表示輸出數據包速率的增量,L2表示節點緩存區的隊列長度,L02表示節點緩存區隊列長度的穩態值,ΔL02表示節點緩存區的隊列長度的增量。

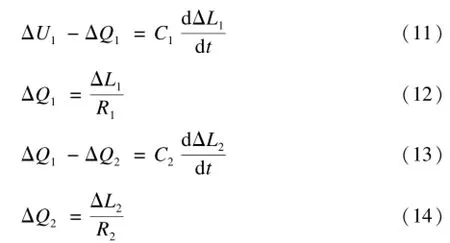
其中,C1和C2為2個節點的緩沖區隊列的容量系數;R1和R2為節點輸出變化與緩沖區隊列變化的比例系數,將式(12)和式(14)代入式(13),得到:

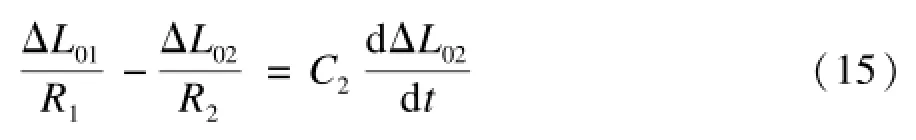
因此,有:

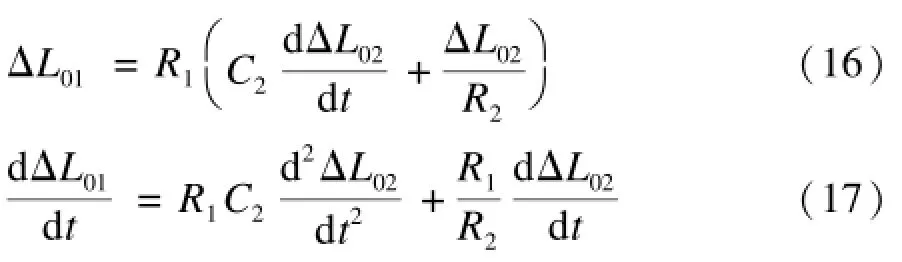
把式(12)代入式(11):

將式(16)和式(17)代入式(18),得到:

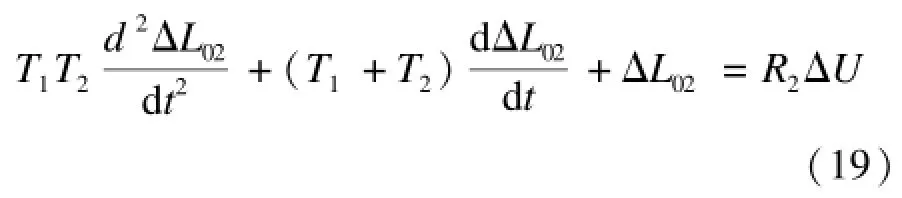
其中,T1=R1C1為第1個節點的時間常數,T2=R2C2為第2個水槽的時間常數。在零初始條件下,對上式進行拉氏變換,得到串聯節點的傳遞函數:

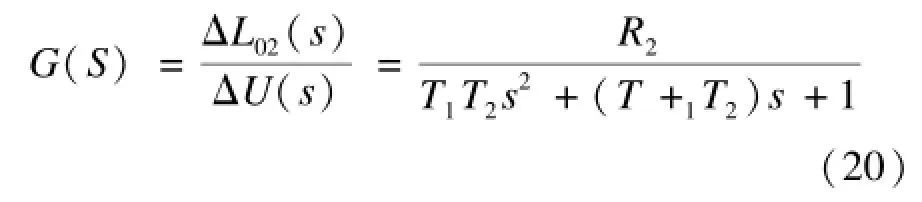
4 對比仿真

無線傳感器網絡擁塞控制算法的性能是網絡QoS的重要指標,采用常規PID進行擁塞控制容易出現隊列長度抖動、時間延遲長和響應速度慢等問題,采用改進的模糊自適應PID算法難以應對無線傳感器網絡應用環境嚴重不確定性;為此,本文采用滑模變結構控制網絡擁塞。該算法具有快速響應、對參數變化及擾動不靈敏、無需系統在線辨識,物理實現簡單等優點,且基于趨近律的滑模控制更能減少節點隊列抖動問題［11］。

在算法的仿真過程中,為防止由于輸出超過隊列長度導致數據包溢出發生,通過不斷的調試,確定PID控制參數和模糊自適應參數控制參數,使其不出現超出隊列長度的抖動。針對方程式(10),單節點一階傳遞模型,令R=3,采樣時間為1 ms,取滑模參數T=3,C=1,q=200。采用控制律式:

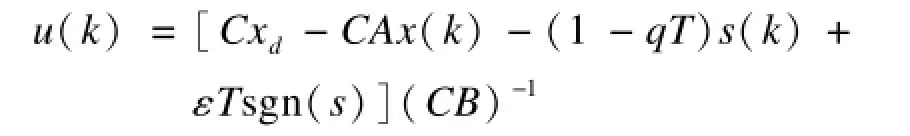
取ε=0.05,按照上面網絡參數選取,對3種算法在瞬時隊列長度進行比較,如圖5和圖6所示。

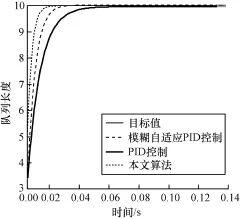
圖5 單節點隊列長度仿真結果

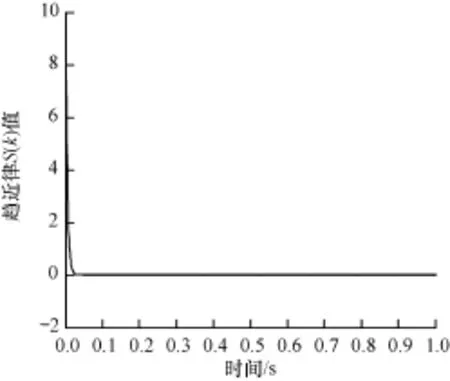
圖6 本文算法趨近律仿真結果1

由于網絡的不穩定性,最大隊列長度可能變化,本文假設在采樣次數K=200時目標值出現變化,仿真結果如圖7所示。

圖7 目標隊列長度發生變化時的仿真結果1

針對方程式(20),多節點傳遞模型,令R2=3,T1=1,T2=1,采樣時間為1 ms,取q=50,ep=0.5,C=［32 1］;采用控制律式:

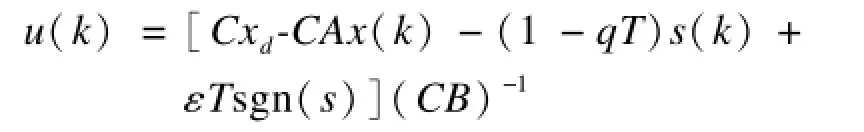
取ε=0.05。在保持模糊自適應控制和PID控制不出現抖動的情況下,按照上面網絡參數選取,對3種算法在瞬時隊列長度進行比較,如圖8和圖9所示。

同樣,針對二階,假設在采樣次數K=1 000時,目標值發生變化,仿真如圖10所示。

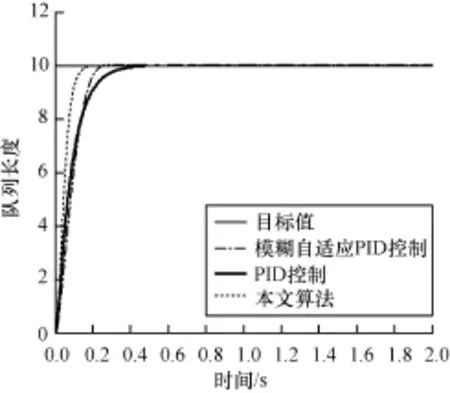
圖8 多節點隊列長度仿真結果

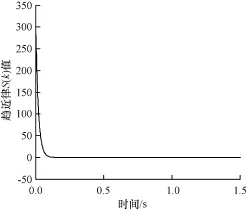
圖9 本文算法趨近律仿真結果2

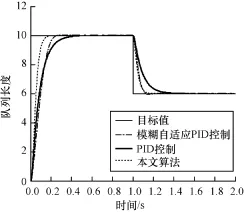
圖10 目標隊列長度發生變化時的仿真結果2

由圖5和圖8可以看出,本文算法很快保持目標隊列長度,響應時間較短,使路由器中的數據接收和發送能夠達到一個平衡,降低緩存中隊列長度從而降低數據傳送的延時,由圖6和圖9可知,本文算法可以保證良好的趨近律品質,滑模運動響應速度快,避免了網絡的延遲和擁塞的發生。圖7和圖10表明,本文選取的趨近律算法,在出現目標值發生變化時,依然可以保持響應速度快、延遲短,能較好地跟蹤目標值。

5 結束語

本文把單容水槽和雙容水槽流入與流出平衡關系應用到無線傳感器網絡擁塞控制當中,用基于趨近律的離散滑模變結構控制幀緩沖區隊列長度。仿真效果表明,本文算法能夠有效地降低隊列排隊延時,使無線傳感器網絡中的節點隊列長度快速、穩定地收斂于期望值,而且無抖動。本文在無線傳感器網絡擁塞開環控制方面,提出一種新的方法,但還需要在實際的無線傳感網絡中,調整模型參數,驗證其控制性能。

［1]李明維,井元偉,陳向勇.一種無線傳感器網絡跨層擁塞控制算法［J］.東北大學學報,2012,33(1):10-20.

［2]Iyer Y G,Gandham S,Venkatesan S.STCP:A Generic TransportLayerProtocolforWirelessSensor Networks［C］//ProceedingsofIEEEICCCN’05.SanDiego,USA:IEEE Press,2005:7-19.

［3]Wan C,Eiseman S,Cambell A.CODA:Congestion Detection and Avoidance in Sensor Networks［C］// Proceedings of the 1st ACM Conference on Embedded Network Sensor Systems.New York,USA:ACM Press, 2003:266-279.

［4]楊歆豪,陸錦軍,王執銓.無線傳感器網絡中基于最小速率的擁塞控制算法［J］.信息與控制,2010,39(5): 513-518.

［5]Maciej Z,Sarangapani J.Predictive Congestion Control Protocol forWirelessSensorNetworks［J］.IEEE TransactionsonWirelessCommunications,2007, 6(11):3955-3963.

［6]石為人,唐云建,王燕霞.基于擁塞控制的無線傳感器網絡數據匯集樹生成算法［J］.自動學報,2010, 36(6):823-828.

［7]胡壽松.自動控制原理［M］.北京:科學出版社,2007.

［8]Chen Shu-Ching,Shyu Mei-Ling,Zha Cheng-jun,et al.A Novel Rate-based Hop-by-Hop Congestion Control Algorithm［C］//ProceedingsofIEEEInternational Conference on Multimedia and Expo.Washington D.C., USA:IEEE Press,2004:245-248.

［9]楊育榮,陳星陽,王保印,等.基于趨近律的離散滑模位置跟蹤控制［J］.指揮控制與仿真,2008,30(2): 42-44.

［10]劉金琨.滑模變結構控制［M］.北京:清華大學出版社,2012.

［11]王宏偉,井元偉.一類不確定離散網絡系統的全局滑模控制［J］.系統工程與電子技術,2011,33(6):1367-1406.

編輯 金胡考

Wireless Sensor Network Congestion Control Based on Sliding-mode Variable Structure

CHEN Shu,WANG Fudong
(School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China)

A new hop-to-hop congestion mathematical model between the network-layer and the link-layer is presented based on the tank balance relationship of the inflows and outflows for the node-congestion control in Wireless Sensor Network(WSN).The congestion control model is simpler than ever before and is easy to implement and a discretesliding mode controller is designed based on the reaching-law.The simulation results show that the proposed model is better than the traditional PID and fuzzy control in terms of response and delay.

Wireless Sensor Network(WSN);congestion control;discrete sliding-mode control;reaching-law;slidingmode variable structure

陳 樹,王夫棟.基于滑模變結構的無線傳感器網絡擁塞控制［J］.計算機工程,2015,41(3):37-40,46.

英文引用格式:Chen Shu,Wang Fudong.Wireless Sensor Network Congestion Control Based on Sliding-mode Variable Structure［J］.Computer Engineering,2015,41(3):37-40,46.

1000-3428(2015)03-0037-04

:A

:TP393

10.3969/j.issn.1000-3428.2015.03.007

國家自然科學基金資助項目(21206053);江蘇省“六大人才高峰”基金資助項目(2012-WLW-006)。

陳 樹(1969-),男,副教授,主研方向:過程控制與優化,無線傳感器網絡;王夫棟,碩士研究生。

2014-03-28

:2014-05-19E-mail:dongliangongsi2008@163.com