長方體破片侵徹明膠的運動模型與實驗研究

莫根林，吳志林，馮杰

(1.江蘇大學 機械工程學院，江蘇 鎮江212013;2.南京理工大學 機械工程學院，江蘇 南京210094)

0 引言

彈藥破片常預制成需要的形狀如球形、菱形(平行六面體)、小箭形等，裝入套筒式彈體中，靠彈丸內的炸藥或拋射藥使其獲得必要的初速以殺傷目標［1］。創傷彈道學中，常采用明膠作為人體組織的替代物研究破片對人體的殺傷機理［2］。

球形破片在明膠中的運動可看作一維直線運動。Sturdivan［3］、Nennstiel［4］、Seglets［5］均將球形破片的受力表示為:F =(cDv2+cVv +cS)S，其中cD、cV和cS分別為動態阻力系數、粘性阻力系數和靜態阻力系數，S 為球形破片的迎風面積。Sturdivan［3］假設靜態阻力系數cS為0，根據流體邊界層理論，將粘性阻力系數cV表示為粘度和邊界層厚度的函數;Nennstiel［4］假設cV和cS為0，根據實驗數據擬合了球形破片的動態阻力系數cD. Seglets［5］假設球形破片的受力和明膠的應變率相關，將cS表示為應變率的函數。Liu 等［6］考慮了球形破片侵徹明膠的分離角，將破片的迎風面積表示為分離角的函數。對于非球形破片，文獻［3］假設破片撞擊明膠表面時存在一定的動量損失，通過擬合實驗數據得到了立方體破片和柱形破片穩定侵徹階段的的阻力系數;該模型以破片的平均迎風面積作為實際迎風面積，沒有考慮破片姿態對侵徹過程的影響。

Eisler 等［7］假設質點在明膠中的受力為速度的二次多項式，以此推導了一維桿的受力方程。Peters等［8］假設彈頭為剛性體，彈頭表面微元的受力由靜力項和動力項組成，其中靜力項為常數、動力項為明膠密度和法向速度平方的乘積，并認為該模型可以較好地預測彈頭攻角0.5° ～3.0°內的運動，不能預測彈頭大翻滾的情況。文獻［9 -11］將旋轉體彈頭微元的受力表示為微元速度的二次多項式，較好地模擬了彈頭在鋁板、混凝土靶、巖石靶和鋼板的侵徹過程。本文擬采用這種表面受力積分的方法建立長方體破片侵徹明膠的受力模型，并開展相應的實驗研究。

圖1 長方體破片的瞬時空腔Fig.1 Temporary cavity in gelatin

1 問題描述

球形破片侵徹明膠時，其運動可看作直線運動，明膠中的瞬時空腔是錐形。而長方體破片侵徹明膠時，破片的運動是空間的。明膠中形成的空腔也不是錐形，如圖1 所示。顯然球形破片的一維運動模型不能用于描述長方體破片的運動，需要建立長方體破片的六自由度運動模型。對于剛性體而言，只需要獲得長方體破片所受的外力。

2 模型

2.1 模型假設

1)假設長方體破片為剛性體，不考慮破片侵徹過程中的彈塑性變形。首先長方體破片(45#鋼)的彈性極限較小(應變小于0.2%)［9］，破片的彈性變形不可能很大;其次實驗收集的破片沒有明顯的塑性變形。

2)根據文獻［10 -12］，假設微元面侵徹明膠時的接觸應力為f，它可以表示為

式中:cDe為動態阻力系數;cSe為靜態阻力系數;v 為面元的速度;dS 為微面元的面積;n 為面元的外法線方向。

該假設中微元面所受壓力由動力項cDe(vn)2和靜力項cSe構成。球形破片侵徹明膠的實驗表明，將cSe視為常數能較好地模擬破片的運動規律［3-4，6］。文獻［13］采用面元積分的方法，對直徑3.0 mm、4.0 mm和4.8 mm 球形破片的實驗數據進行了擬合，確定了球形破片的靜態阻力系數cSe= -560 000 kg/ms2. 由于靜力項可理解為明膠剪切破壞所產生的阻力，這里假設長方體破片的靜態阻力系數和球形破片的相同。動力項可理解為微元推動迎風面明膠運動所產生的阻力。由于流場的分布和破片的外形有關，長方體破片的動態阻力系數和球形破片的可能不同。本文將通過試算得到長方體破片的動態阻力系數。

2.2 幾何和運動學參數

長方體破片的尺寸參數如圖2 所示，令AB、BC和CD 三邊的長度分別為a、b、c;在長方體破片的幾何中心O 建立直角坐標系Oxyz，其中Ox 平行于AB、Oxy 平行于底面ABC、Oz 垂直底面向上。令Ox、Oy 和Oz 三軸的基矢量分別為i、j、k.

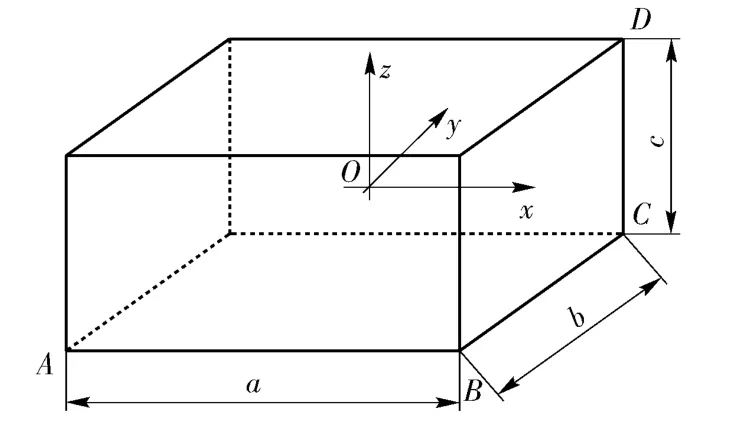
圖2 長方體破片的尺寸參數Fig.2 Dimensions of cuboid fragment

建立固定坐標系O'x'y'z'，令O'x'、O'y'、O'z'三軸的基矢量為i'、j'、k'. 以歐拉角描述連體坐標系Oxyz 相對坐標系O'x'y'z' 的轉動，其中φ、ψ 和θ分別表示自轉角、進動角和章動角，令θ 為Oz 軸與O'z' 的夾角。破片表面任意點的矢徑r'可表示為

破片表面任意點的速度v'可表示為

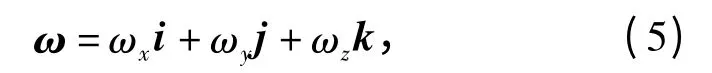
ωx、ωy和ωz分別為角速度在x、y 和z 方向的分量，表達式為

r'處微元的面積dS 可表示為

式中:dx 為坐標增量;s、t 為自由指標，但s≠t.

由于坐標系Oxyz 的坐標軸和長方體破片的三邊平行，r'處微元的外法線方向n 為

將(4)式、(7)式和(8)式帶入(1)式可求得任意位置點的受力f. 將f 對質心O 點取矩得

2.3 運動方程

根據高等動力學理論［14］，破片的質心運動方程可以表示為

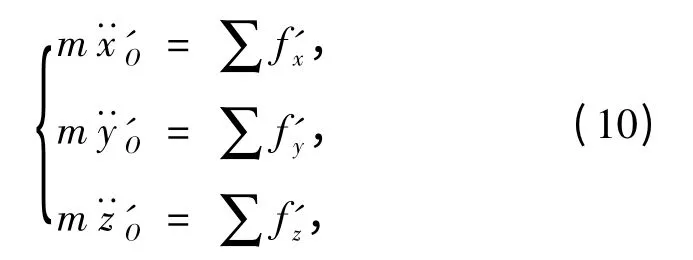
破片推廣的歐拉運動方程可以表示為

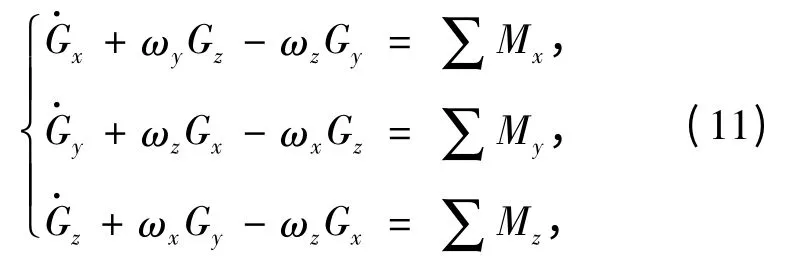
式中:

Jx、Jxy、Jyz、Jy、Jxz和Jz為破片對Oxyz 坐標系的慣性張量分量;∑Mx、∑My和∑Mz為破片繞x、y和z 軸的力矩分量。

對(6)式、(10)式、(11)式和(12)式整理，得長方體破片侵徹明膠的六自由度運動方程:

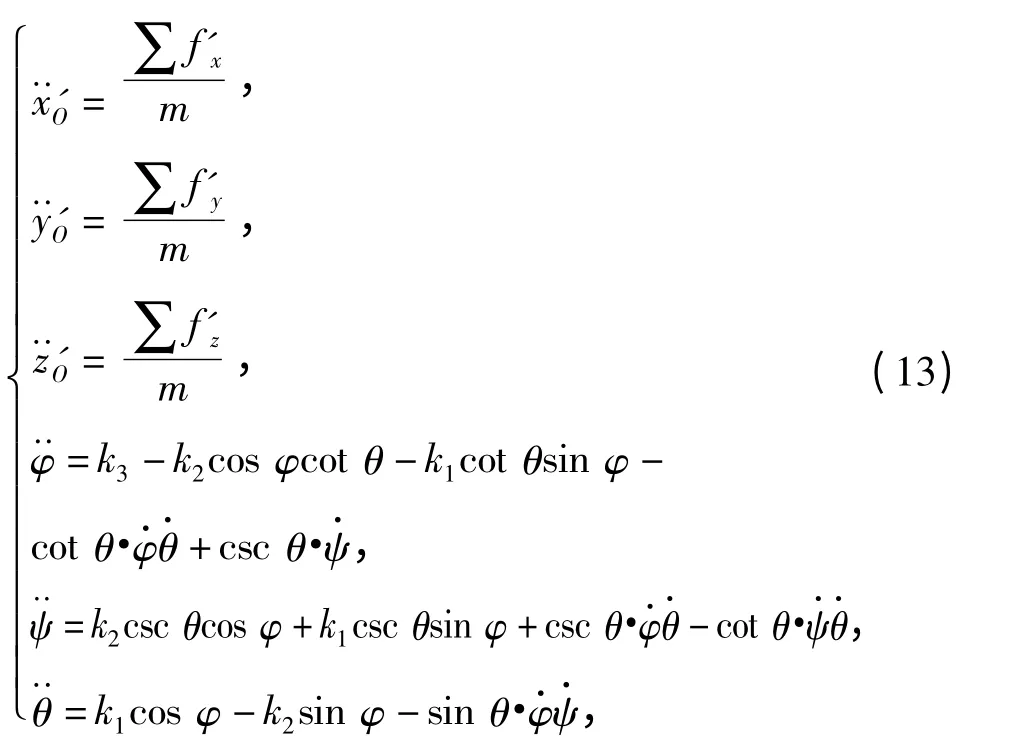
式中:k1、k2和k3為

H1、H2和H3分別為

2.4 算例

令均質長方體破片的密度為7.9 g/dm3，三邊的長度a、b、c 分別為2.0 mm、2.0 mm 和2.5 mm，其初始姿態角φ、ψ、θ 分別為10°、10°和10°. 令該長方體破片的動態阻力系數為400 kg/m2. 破片沿z'軸以500 m/s 入射明膠，其質心位移隨時間的變化如圖3 所示。破片x'方向的位移為負值，先變小后變大，最小值為-5.0 mm;y'正方向的位移為正值，先變大后變小，最大值為13.2 mm;z'方向的位移也為正值，從0 逐漸增加到130.1 mm. 破片歐拉角隨水平侵徹位移的變化如圖4 所示。長方體破片水平侵徹距離達到最大過程中，歐拉角逐漸停止變化，其中，ψ 穩定為11.9°，φ 穩定為8.0°，θ 穩定為6.6°.

圖3 質心位移隨時間的變化Fig.3 Displacement vs. time

圖4 歐拉角隨位移的變化Fig.4 Euler angle vs.

3 實驗驗證

實驗中，明膠塊由10%的彈道明膠制成，尺寸為30 cm×30 cm×30 cm. 明膠塊使用前在4 ℃保溫箱中保溫24 h. 彈道槍發射2 發長方體破片，槍口距離明膠塊表面5 m. 表1 為實驗長方體破片的外形參數，破片質量為0.151 g. 采用幀頻1.5 MHz 的高速攝影拍攝破片在O'y'z' 平面的運動，拍攝角度如圖5 所示。高速攝像機的像素分辨率為0.7 mm/像素。采用Phantom camera control 軟件讀取質心位移數據時，容易造成1 ～2 個像素的誤差。本文采用getdata 軟件讀取破片的質心位移，一定程度上克服了分辨率不足的缺點。

表1 長方體破片的外形參數Tab.1 Shape parameters of the fragment

圖5 高速攝像機和明膠塊的相對位置Fig.5 Schematic of positions of the high-speed camera and gelatin block

以破片進入明膠前連續兩幀的平均速度作為破片的初始速度。假設破片在x' 方向的速度為0，2 發長方體破片的初始位移和初始速度如表2 所示。

表2 長方體破片的初始位移和初始速度Tab.2 Initial displacements and initial velocities

長方體破片入靶前連續兩幀在O'y'z' 平面的投影保持不變，可認為其角速度為0. 根據平面投影，可試算得到實驗長方體破片的初始歐拉角。2 發長方體破片模型投影和實驗投影的比較如圖6 所示。表3 為長方體破片的初始歐拉角和角速度。

圖6 長方體破片的平面投影Fig.6 Initial projections of cuboid fragments

通過試算可知，cDe=572 kg/m3時2 發長方體破片在水平方向和豎直方向的位移誤差較小。1號破片在z'方向位移理論值和實驗值的比較如圖7 所示，最大誤差為1.4 mm，平均誤差為0.67 mm;圖8為1號破片y'方向位移和時間的關系，模型的最大誤差為0.97 mm，平均誤差0.22 mm.

表3 長方體破片的初始歐拉角和初始角速度Tab.3 Initial Eulerian angles and the initial angular velocities of the first fragment

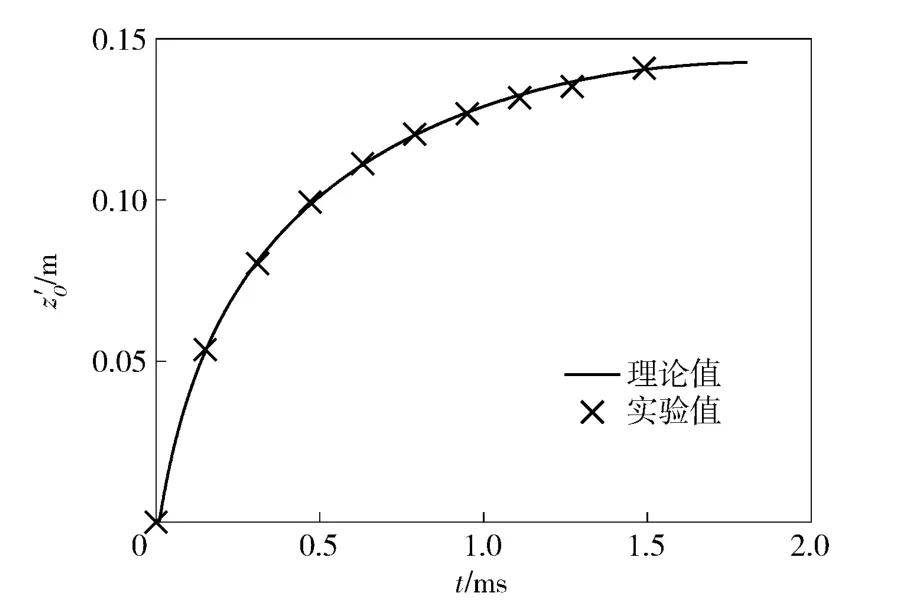
圖7 1號實驗破片隨時間的變化Fig.7 vs. t of Fragment 1

2號破片z'方向侵徹位移理論值和實驗值的比較如圖9 所示，最大誤差5.9 mm，平均誤差3.9 mm;圖10 為2號破片y'方向侵徹位移和時間的關系，模型的最大誤差為1.2 mm，平均誤差0.62 mm.

考慮實驗數據的讀取誤差，以及長方體破片幾何誤差、初始參數誤差等對理論值的影響，可認為1號和2號長方體破片的位移誤差是較小的。表明模型獲得的動態阻力系數是合理的。

4 結論

圖8 1號實驗破片隨時間t 的變化Fig.8 vs. t of Fragment 1

圖9 2號實驗破片隨時間t 的變化Fig.9 vs. t of Fragment 2

圖10 2號實驗破片隨時間t 的變化Fig.10 vs. t of Fragment 2

實驗研究表明長方體破片侵徹明膠過程中，除了質心的平移運動還有劇烈的空間翻滾運動。本文基于長方體破片侵徹明膠的接觸假設和接觸面的應力分布假設，建立了長方體破片侵徹明膠的六自由度運動模型。實驗表明該模型能夠較好地描述長方體破片侵徹明膠的空間運動規律。通過試算法，本文獲得了長方體破片的動態阻力系數。該模型的建立為進一步評估長方體破片的殺傷效能和優化設計提供了參考依據。

References)

［1］王儒策，趙國志. 彈丸終點效應［M］. 北京:北京理工大學出版社，1994:83 -84.WANG Ru-ce，ZHAO Guo-zhi.Terminal ballistic effect［M］. Beijing:Beijing Institute of Technology Press，1994:83 - 84. (in Chinese)

［2］劉蔭秋，王正國，馬玉媛. 創傷彈道學［M］. 北京:解放軍出版社，1991:32 -33.LIU Yin-qiu，WANG Zheng-guo，MA Yu-yuan. Wound ballistics［M］. Beijing:Chinese People's Liberation Army Press，1991:32 -33. (in Chinese)

［3］Sturdivan L M. A mathematical model of penetration of chunky projectiles in gelatin tissue stimulant，ADA063526［R］. MD，US:Aberdeen Proving Ground，1978.

［4］Nennstiel R. Once again-spheres in gelatin［J］. Journal of Trauma，1990，6(2):119 -124.

［5］Seglets S B. Modeling the penetration behavior of rigid into ballistic gelatin，ARL-TR-4393［R］. MD，US:Aberdeen Proving Ground，2008.

［6］Liu L，Fan Y，Li W，et al. Cavity dynamics and drag force of high-speed penetration of rigid spheres in to 10 wt% gelatin［J］.International Journal of Impact Engineering，2012，50:68 -75.

［7］Eisler R D，Chatterjee A K，Burghart G H，et al. Simulates the tissue damage from small arms projectiles and fragments penetrating the musculoskeletal system，ADA54311［R］. MD，US:Aberdeen Proving Ground，1998.

［8］Peters C E，Sebourn C L，Crowder H L. Wound ballistics of unstable projectiles.Ⅰ. projectile yaw growth and retardation［J］.Journal of Trauma，1996，40(3S):10 -15.

［9］任志俊，薛國祥.實用金屬材料手冊［M］. 南京:江蘇科學技術出版社，2007:237.REN Zhi-qiang，XUE Guo-xiang. Pratical handbook of metallic materials［M］. Nanjing:Jiangsu Science and Technology Press，2007:237. (in Chinese)

［10］Warren T L，Tabbara M R. Spherical cavity-expansion forcing function in PRONTO 3D for application to penetration problems，SAND-97-1174［R］. Albuquerque，NM，US:Sandia National Labs，1997.

［11］Warren T L. Simulations of the penetration of limestone targets by ogive-nose 4340 steel projectiles［J］. International Journal of Impact Engineering，2002，27(5):475 -496.

［12］Satapathy S，Bless S. Response of long rods to moving lateral pressure pulse:numerical evaluation in DYNA3D［J］. International Journal of Impact Engineering，2001;26(1):663 -674.

［13］Mo G L，Wu Z L，Liu K. Drag force analysis of spheres penetrating gelatin based on surface integral［J］. Applied Mechanics and Materials，2012，105 -107:561 -565.

［14］張延教. 高等動力學［M］. 南京:華東工學院，1984:56 -280.ZHANG Yan-jiao. Advanced dynamics［M］.Nanjing:East China Institute of Technology，1984:26 -280. (in Chinese)