場域中填充多介質且存在3種以上介質公共點或公共線的電磁場邊值關系及其應用

王禮祥 蔡 書

(西南民族大學預科教育學院，四川 成都 610041)

?

場域中填充多介質且存在3種以上介質公共點或公共線的電磁場邊值關系及其應用

王禮祥 蔡 書

(西南民族大學預科教育學院，四川 成都 610041)

文章分析討論了場域空間填充有多介質且存在3種以上介質公共點或公共線上的電磁場邊值關系一般形式，就簡單可解的多介質分界面與電場線重合和多介質分界面與等勢面重合的特殊情況舉例說明其應用.結果表明多介質公共點或公共線上的邊值關系并非是簡單的兩、兩介質分界面邊值關系的組合，多介質公共點或公共線上的邊值關系確有必須遵循的特殊形式.

麥克斯韋方程；電磁場邊值關系；靜電場；電介質；多介質公共點；多介質公共線

眾所周知，由電磁場積分形式的麥克斯韋方程組

可以導出電磁場的邊值關系

說明電磁場邊值關系只是積分形式的麥克斯韋方程組在兩介質分界面上的特殊形式，它是因為介質性質的突變(ε和μ突變)或分界面上存在自由電荷面分布與電流面分布從而導致電磁場的場量突變而必須遵循的客觀規律.我們在文獻[2]、[3]中給出了它的推廣應用形式，即在場域內任意選取的任何曲面上式(2)同樣成立，因為普遍適用的積分形式麥克斯韋方程組在人為選取的任意曲面兩側場量可能連續也可能突變，它取決于曲面上有無點電荷、線電荷與線電流.本文分析討論給出場域內填充多種分區均勻介質時出現多介質公共點或公共線上的電磁場邊值關系的具體形式，并就特殊可簡單求解情況舉例說明其重要應用，為便于行文僅以靜電場邊值關系為例闡述分析.

1 多介質填充場域時公共點或公共線上的靜電場邊值關系

靜電場的基本特征是其分布不隨時間變化，描述靜電場力的性質的物理量電場強度矢量和描述靜電場能量性質的物理量電勢都只是空間點的函數，在兩介質分界處靜電場的場量點點對應邊值關系是

或者以電勢表達為

式(3)或式(4)闡明了兩種介質分界面上點點對應的靜電場場量突變關系，是介質性質突變導致場量的突變，點點對應或點點趨近對應是極限關系.

場域空間總是由點、線、面構成，當靜電場空間內填充多種分區均勻介質時不可避免地要出現3種或3種以上介質相鄰的公共點或公共線，這時多介質公共點或公共線上的邊值關系到底是什么樣的？各類型文獻資料中都沒有具體闡明，原因可能是:① 認為分別應用兩兩介質分界面上的邊值關系即可解決問題；② 是此類問題只有特殊情況下有簡單解(介質分界面與電場線重合或介質分界面與等勢面重合)，一般情況下不一定存在解析解.本文應用宏觀電磁場理論中的宏觀小微觀大思想，將點、線放大分析討論多介質公共點或公共線之邊值關系并以極限方法給出簡明結論.

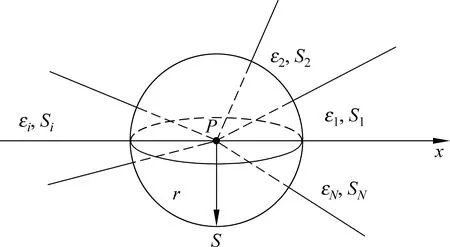
圖1 多介質公共點P圖示

如圖1所示，設靜電場空間內填充有N種分區均勻電介質(ε1，ε2，ε3，…，εi,…,εN)，各介質內的電場強度矢量分別是E1，E2，E3，…，Ei,…,EN；電勢是φ1，φ2，φ3，…，φi,…,φN；它們存在一個公共點P，以P為球心作一半徑為r(r→0)的球面，應用靜電場高斯定理可得

式中S=S1+S2+…+SN.

且兩兩介質分界面上的邊值關系照樣成立，即ε1與ε2分界面上有

ε2與ε3分界面處有

εN與ε1分界面處有

注意以上N個式子分別是N個介質分界面上非公共點外的邊值關系，是空間點坐標函數關系(每個關系式為一個界面上同一點處的場量關系)，結合式(5)即得N種介質公共點P處的邊值關系:

即多介質公共點處的靜電場邊值關系

當多介質公共點處存在點電荷Q時，其靜電場邊值關系為

多介質場域存在3種以上介質公共線時類似于多介質公共點分析，只是要在放大公共線呈直線段后取包圍直線段的圓柱面為高斯面討論，同樣可得到相應靜電場邊值關系:

(1)公共線上無線電荷分布,公共線上的邊值關系為

(2)公共線上存在線電荷λ，取包圍線電荷λ的圓柱高為h，公共線上的邊值關系為

特殊情況下，當介質分界面與電場線重合時[4]，如點電荷Q位于多介質錐公共頂點P的靜電問題或無限長直線線電荷λ位于多介質公共線上的靜電問題，都有下面簡單電勢解:

① 點電荷Q位于N種介質錐公共點P的簡單球對稱電勢解[5]

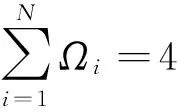
② 無限長直線線電荷λ置于N介質無限公共直線上的柱對稱電勢解[6]

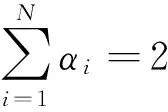
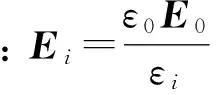
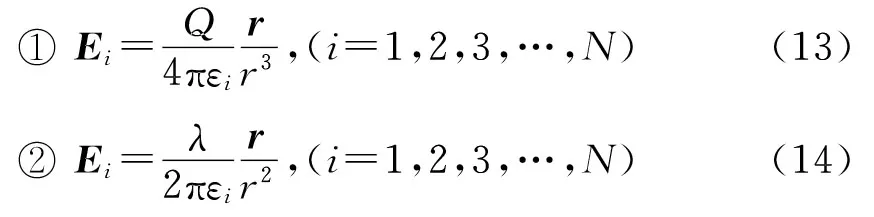
3 應用實例——點電荷非對稱雙介質錐問題

設圖2所示為非對稱雙介質圓錐公共頂點O處放置點電荷Q，兩介質圓錐公共線為y軸正半軸，真空對O點的立體角為Ω3.驗證三介質公共點和公共線邊值關系成立.

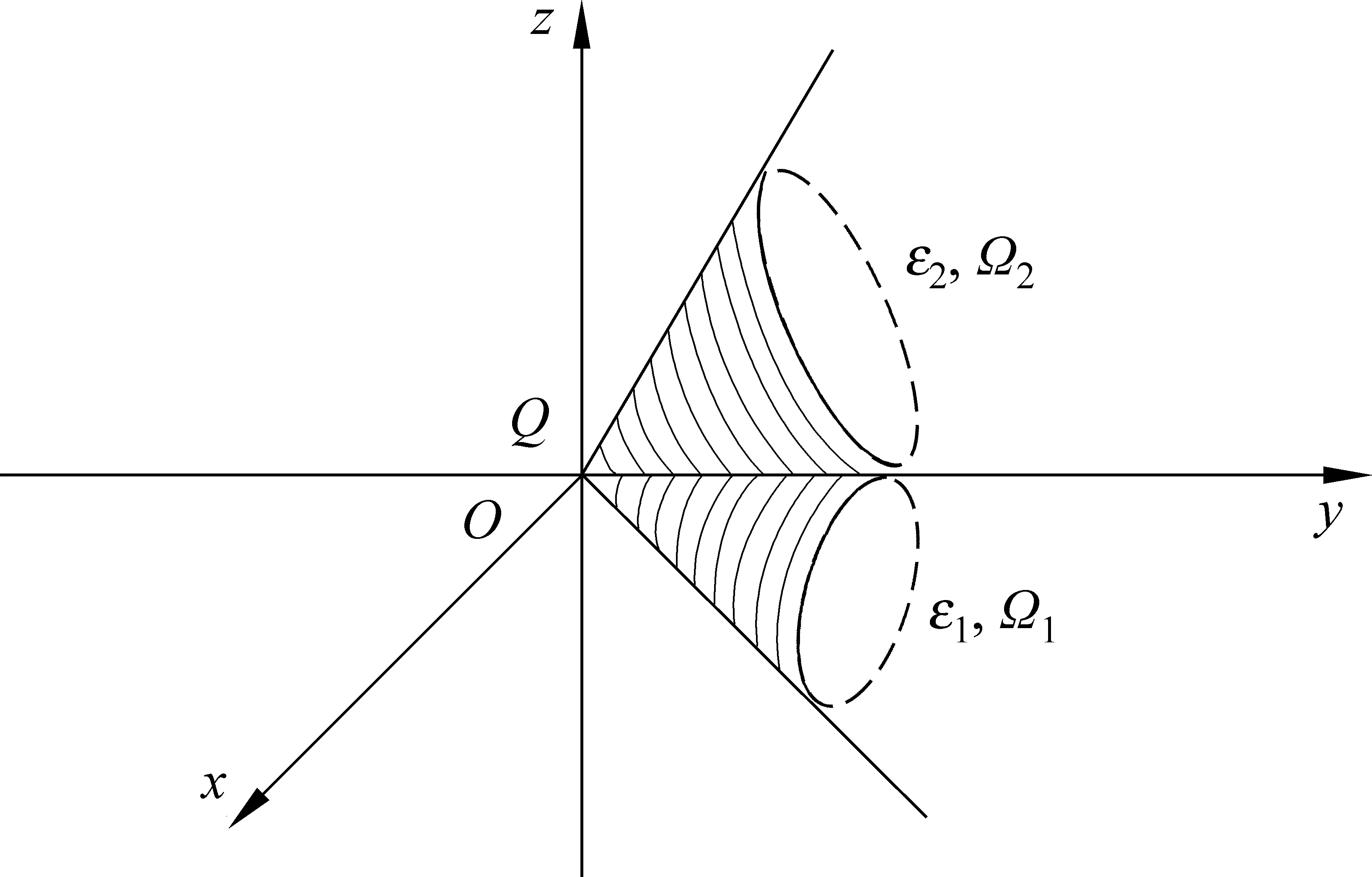
圖2 點電荷非對稱雙介質錐

由“帶電導體球與介質錐靜電問題解及推廣應用”[7]給出該問題的球對稱解

去證明三介質公共點和公共線上的邊值關系成立:

① 坐標原點(公共點)O的邊值關系

把式(13)代入式(7)得

注意點電荷是理想化模型并非真正意義的r=0而r→0，所以(式(16)、(17))說明三介質公共點處的邊值關系成立.

② 三介質公共線y軸正半軸上的邊值關系

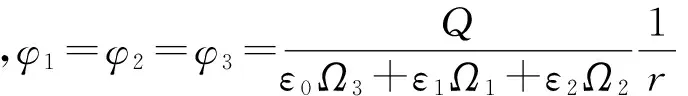
[1] 科學出版社名詞室合編.物理學詞典(上冊)[M].北京： 科學出版社,1988：2-3～2-5.

[2] 王禮祥.電磁場邊值關系的一種證明及其推廣應用[J].西南民族學院學報(自然科學版)，1993(02):150-155.

[3] 王禮祥.電磁場邊值關系的推廣應用[J].大學物理，1994(11)，8-12.

[4] 胡友秋,程福臻,葉邦角,等.電磁學與電動力學(上冊)[M].2版.北京： 科學出版社,2014： 57-61.

[5] 曲世光.點電荷位于多種介質錐公共頂點時的勢[J].大學物理，1998(04)： 45-46.

[6] 曲世光.共頂(軸)多介質錐(楔)中球(軸)對稱靜電場及其一般公式[J].哈爾濱電工學院學報,1987(02)：176-181.

[7] 王禮祥,蔡書.帶電導體球與介質錐靜電問題解及推廣應用[J].西南民族學院學報(自然科學版),2004(02):166-169.

■

ELECTROMAGNETIC FIELD BOUNDARY VALUE RELATIONS ON PUBLIC POINT OR LINE OF THREE OR MORE MEDIA AND ITS APPLICATIONS

Wang Lixiang Cai Shu

(School of Preparatory Education,Southwest University for Nationalities,Chengdu,Sichuan 610041)

In this paper,we analyzed and discussed the general form of electromagnetic field boundary value relations on the public point or line of three or more media.We illustrated its applications by two simple solvable special examples,which are the superposition of multi-media interface with electrostatic field lines and the superposition of multi-media interface with equipotential surface.The results showed that boundary value relations on multi-media public point or line were not the simple combinations of the boundary value relations of two or more media interface,and there were special forms that must be followed.

Maxwell’s equations;electromagnetic boundary value relation;electrostatic field;dielectric;electrostatic field boundary relation;multi-media public point;multi-media public line

2015-02-08

王禮祥，男，西南民族大學預科教育學院副教授，主要從事物理教學、計算機基礎教學和科研.ykbw@163.com