車載導彈光學輔助數學傳遞對準方法

梁浩，王丹丹，穆榮軍，崔乃剛

(1.哈爾濱工業大學 航天學院，黑龍江 哈爾濱150001;2.北京宇航系統工程研究所，北京100076)

0 引言

車載導彈發射前處于低速或靜止狀態，在現代快速響應戰爭環境下，發射車從占領發射陣地至導彈發射這段時間內是比較脆弱的，容易遭受打擊，發射準備時間是評價現代車載導彈射前生存能力的重要技術指標［1］。

初始對準和彈車系統測試是車載導彈發射前需要完成的兩項主要工作。隨著電子技術的發展，彈車系統測試工作所需的時間越來越短，部分測試工作可以在行駛途中完成;而導彈瞄準工作需要在發射車停止后進行，并且需要占用較長的時間。如何縮短導彈初始對準時間，降低對準系統對發射場坪、環境條件的要求，是車載導彈快速發射技術需要解決的關鍵問題。

車載導彈初始對準方式主要有光學瞄準、自對準和傳遞對準等。光學瞄準精度高，但需要在發射陣地靜態進行，配套設備要求高、占時長、自動化程度低［2］。自對準依靠慣導自身的輸出完成對準，不需要外界信息，但對準精度受慣性器件工藝制約和環境干擾影響，且方位角對準時間長，很難滿足高精度快速初始對準的要求。傳遞對準［3］需要配備高精度主慣導，并對載車機動形式有一定要求。

本文針對車載導彈快速高精度初始對準的需求，將光學瞄準和常規傳遞對準相結合，提出了利用自準直儀輔助數學傳遞對準的方法。推導了發射陣地主、子慣導方位傳遞關系，建立了傳遞對準數學模型，將光學準直得到的相對方位測量角引入到“角速度+加速度”匹配模式中構成新的量測方程，對主、子慣導安裝角進行濾波估計，并通過仿真對比分析，驗證了新方法的優越性。

1 快速發射傳遞對準方法分析

目前常用的數學傳遞對準匹配模式主要有計算參數匹配和測量參數匹配兩種。計算參數匹配法(如“速度+姿態”匹配)魯棒性好、抗噪聲能力強，但對準速度較慢，且對發射車機動形式有一定要求，在實戰中，發射車質量較大且受地形地貌的限制不能保證提供足夠的姿態機動［4-6］;測量參數匹配法(如“角速度+加速度”匹配)實時性強，水平姿態角對準速度快、精度高，但抗干擾能力有限，方位失準角估計精度差，適用于發射車靜止或運動狀態平緩的情況［7-8］。

本文提出的車載導彈光學輔助數學傳遞對準方法利用自準直儀測量主、子慣導的相對方位關系，利用數學傳遞對準完成水平姿態角的快速估計，綜合考慮對準時間、精度、載車機動等因素，應選擇“角速度+加速度”匹配模式。

初始對準系統搭建如圖1所示，主要包括車載高精度主慣導、自準直儀、彈上慣導、方位棱鏡、車載計算機等。方位棱鏡與子慣導(彈上慣導)固連安裝，子慣導與主慣導體軸平行，自準直儀與主慣導固連安裝。自準直儀的測量角度范圍為±2 000″，在初始對準系統設備安裝時，要檢驗工裝精度，保證棱鏡反射光線在自準直儀的俘獲范圍內。

圖1 車載導彈初始對準系統組成Fig.1 System composition for initial alignment of vehicle-launched missiles

車載導彈快速發射傳遞對準流程如下:在導彈庫陣地，車載主慣導完成初始對準和標定;發射車開往發射陣地途中，主慣導持續工作，保持姿態基準;發射車到達發射陣地停穩并調平后，完成主、子慣導快速傳遞對準;導彈起豎導航，準備發射。

2 快速發射數學傳遞對準模型

2.1 慣導誤差傳播模型

車載導彈傳遞對準過程中，涉及到主、子兩套慣性導航系統，其誤差傳播特性同單個慣導系統的誤差傳播特性有一定差異。在進行數學傳遞對準建模處理過程中，需要對慣導系統誤差傳播模型中的相關參量進行重新定義和處理，以區別于研究單個慣導時的情形。

主、子慣導均采用捷聯式慣性導航系統，主慣導的導航坐標系記為n 系，子慣導的導航坐標系記為n'系;定義子慣導相對主慣導的安裝角為φa=［φaxφayφaz］T;定義子慣導導航坐標系與主慣導導航坐標系對應坐標軸之間的誤差角為姿態失準角，記為φ=［φxφyφz］T. 則在地理坐標系內，子慣導相對主慣導的誤差傳播模型［9］為

式中:Δωs為子慣導陀螺儀常值漂移;ωnin為主慣導計算導航坐標系相對于慣性參考坐標系的旋轉角速度矢量在其計算導航坐標系中的分量形式;為對應誤差量;fnm為導航系內表示的主慣導的視加速度;ωnen為導航系的位置角速度;為子慣導的速度;Δas為子慣導的加速度計測量誤差;RM、RN為當地子午圈和卯酉圈半徑;λ、L、h 分別為地理經度、緯度和高度。

2.2 數學傳遞對準狀態方程

取狀態向量為

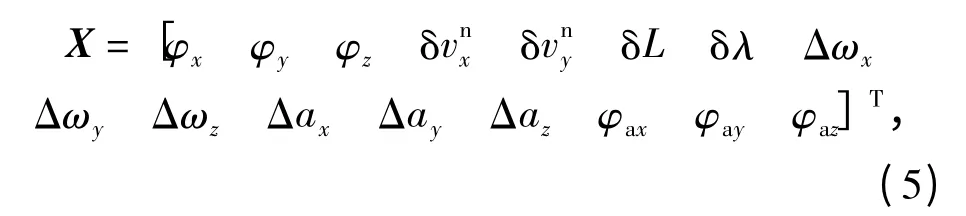
式中:φx、φy、φz為姿態失準角;為主、子慣導東向及北向速度之差;δL、δλ 為經度、緯度之差;Δωx、Δωy、Δωz為子慣導陀螺常值漂移;Δax、Δay、Δaz為子慣導加速度計測量零偏;φax、φay、φaz為主、子慣導安裝角。

系統的狀態方程為

式中:A 為系統狀態轉移矩陣;B 為系統過程噪聲驅動矩陣;W 為系統過程噪聲向量。A、B 中各量由(1)式～(4)式給出的慣導系統誤差傳播方程確定。

2.3 “角速度+加速度”觀測方程

采用“角速度+加速度”匹配模式時，通過觀測主、子慣導的角速度和加速度信息，對主、子慣導安裝角進行估計。

記主慣導測得的角速度和比力分別為ωbm和fbm，子慣導測得的角速度和比力分別為ωbs和fbs，主、子慣導安裝矩陣為Cba. 主、子慣導數學傳遞對準過程中，以主慣導為參考基準，因此，不考慮主慣導陀螺和加表的測量誤差。

主、子慣導測量信息有如下關系:

當安裝角為小量時，有

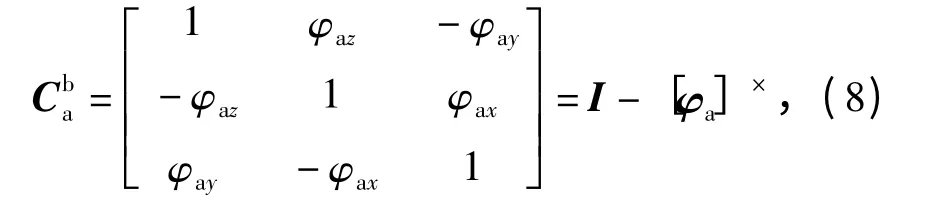
式中:［φa］×為φa構成的反對稱矩陣;φax、φay為水平方向安裝角，可由數學傳遞對準得到;φaz為未知參數。

從而

則系統的觀測向量為

觀測方程為

式中:H 為觀測矩陣;V 為觀測噪聲。

3 慣導方位光學傳遞

如圖2所示，OaXaYaZa、ObXbYbZb分別為主、子慣導體坐標系，Ya指前，Xa指右，Za指上;OaXSYSZS為自準直儀坐標系，P 為方位棱鏡棱脊的單位向量。

OaOb為瞄準儀對棱鏡自準直時的光軸向量，OaOb與P 垂直，AP、θP分別為自準直儀平盤角和豎盤角。

在車載導彈初始對準系統中，方位棱鏡與子慣導固連安裝，自準直儀與主慣導固連安裝，以上設備安裝完成后，需利用經緯儀、水平平臺等設備，借助北向基準，采用常規標定方法對棱鏡安裝誤差角α、β 以及自準直儀與主慣導的安裝矩陣CaS進行標定，本文不再詳述。

設OaOb的單位向量為L，則L 在S 坐標系下表示為

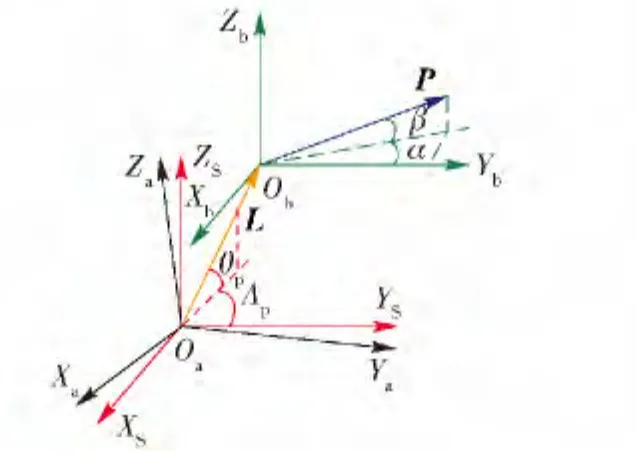
圖2 光學方位傳遞坐標關系Fig.2 Coordinate relation of optical azimuth transfer

則L 在a 系下表示為

火草布,透氣性和保暖性十分好,冬暖夏涼，有棉毛混紡的效果。火草布是傈僳族人衣著的主要材料，制作成衣服、包、被子等生活用品，也是喪葬中必需的用料。中國西南少數民族制作和使用火草布的歷史悠久,文獻記錄已有500多年。衣著為火草衣的民族眾多,包括傈僳族、納西族、彝族、白族等。其采用野生植物的葉子為紡織原料,在中國紡織史上十分獨特且罕見,可以說是西南少數民族的一項重要的創造發明。

由α、β 得到棱脊單位向量在b 系下的分量:

則在a 系下P 向量為

式中:Cba包含φax、φay、φaz3 個安裝角參數。

OaOb與P 垂直，可得

由(8)式、(12)式～(16)式可解出φaz，從而得到安裝角φa和安裝矩陣Cba.

4 光學輔助傳遞對準

根據(15)式可知，在利用方位光學傳遞公式計算φaz之前，首先要知道水平方向安裝角φax和φay的大小。“角速度+加速度”匹配模式傳遞對準對水平安裝角估計精度高、收斂速度快，因此可先通過“角速度+加速度”傳遞對準對φax和φay進行估計。

車載導彈光學輔助數學傳遞對準步驟如下:首先采用“角速度+加速度”匹配模式傳遞對準濾波器對水平方向安裝角φax和φay進行估計，如(17)式中的Z1所示，等待濾波估計收斂后，將φax、φay和自準直儀的測量值帶入方位光學傳遞公式計算主、子慣導相對方位角φaz，最后將φaz與“角速度+加速度”構成新的量測方程Z2，再次進行數學傳遞對準濾波估計，以提高天向安裝角估計的估計精度。

在通過數學、光學傳遞得到子慣導相對于主慣導的安裝角后，可得到子慣導相對于導航坐標系的姿態矩陣，即

式中:Can為主慣導姿態矩陣。

通過Cbn進行姿態角提取，可以得到子慣導相對導航坐標系的姿態信息，從而實現對子慣導姿態角的修正。

5 實驗驗證與分析

5.1 方位光學傳遞實驗驗證

為了驗證慣導方位光學傳遞算法，于2014年3月在哈爾濱工業航天工程系導航與對準實驗室進行了7 次實驗，分別用2 個標準六面體代替主、子慣導，測量設備為經緯儀。方位光學傳遞算法根據標定得到的α、β、CaS、φax、φay以及自準直儀測量得到的AP、θP，計算出φaz，同時，利用經緯儀和六面體對φaz的值進行校準，方位光學傳遞的計算結果與校準結果對比如表1所示。由表1可以看出，7 組實驗中φaz的計算結果和校準結果差值均在3″以內，方位光學傳遞的計算精度較高(誤差主要是由儀器設備誤差以及環境干擾影響造成的)，驗證了算法的正確性。

表1 方位光學傳遞實驗結果Tab.1 Experimental results of optical azimuth transfer

根據導彈快速發射傳遞對準流程，在實際工作中，發射車到達發射陣地，車底盤伸出支腿并調平穩定后，進行主、子慣導快速傳遞對準。因此，實際工作中自準直儀方位光學傳遞的工作環境比較穩定，僅車載設備的振動對光學測量角度的影響較小。

5.2 光學輔助傳遞對準數學仿真分析

5.2.1 仿真條件

1)慣導參數設置:車載主慣導陀螺常值漂移0.003°/h(1σ)，加速度表零偏1 ×10-5g(1σ);彈上子慣導陀螺常值漂移0.01°/h(1σ)，加速度表零偏1 ×10-4g(1σ);主、子慣組數據更新周期為0.01 s，傳遞對準濾波周期為0.2 s.

2)光電設備參數設置:自準直儀瞄準誤差1″，棱鏡α、β 值標定誤差5″，自準直儀、主慣導安裝角標定誤差5″. 預設主、子慣導安裝角為［15'，-15'，10'］，自準直儀與主慣導安裝角為［15'，15'，-10'］，α 為-5'，β 為5'.

5.2.2 數學傳遞對準結果

發射車行駛2 h，到達發射陣地停穩后，在靜止狀態下進行數學傳遞對準，仿真時間100 s，仿真結果如圖3、圖4所示。

圖3 “速度+姿態”模式下安裝角估計誤差Fig.3 Estimated errors of installation angles in“velocity plus attitude matching”mode

兩種匹配模式下傳遞對準精度和濾波估計收斂時間對比如表2所示。

表2 不同匹配模式仿真結果對比Tab.2 Comparison of simulated results for different matching

5.2.3 光學輔助傳遞對準仿真結果

根據(17)式，在“角速度+加速度”傳遞對準收斂后(25 s 以后)，進行光學輔助數學傳遞對準，仿真結果如圖5所示。

圖4 “角速度+加速度”模式下安裝角估計誤差Fig.4 Estimated errors of installation angles under angular rate plus acceleration matching

圖5 光學輔助傳遞對準安裝角估計誤差Fig.5 Estimated errors of installation angles in optically-aided transfer alignment mode

光學方位輔助系統對主、子慣導天向安裝角估計精度有較大提高，估計誤差由常規“角速度+加速度”匹配模式下的15.12＇減小到10″，對水平方向安裝角影響較小。

5.2.4 結果分析

由仿真結果可以看出，在發射車靜止狀態下，由于沒有姿態搖擺的激勵，“速度+姿態”匹配模式收斂速度較慢，安裝角估計精度不高;而“角速度+加速度”匹配模式收斂速度較快(25 s)，水平方向安裝角估計精度也較高(0.36＇、0.33＇)。為了解決天向安裝角的估計精度低問題，引入光學方位輔助系統后，天向安裝角估計精度達到10″，修正時間也較短。改進后的彈上慣導對準方法在對準時間(小于30 s)和對準精度(水平0.36＇、0.33＇，天向10″)兩個方面均取得了較好的效果。

6 結論

經實驗驗證，本文提出的利用自準直儀和棱鏡進行主、子慣導光學方位傳遞的方法精度較高，速度較快。將光學方位傳遞與“角速度+加速度”數學方法相結合進行主、子慣導傳遞對準，既保留了“角速度+加速度”匹配模式水平方向精度高、速度快的優點，又解決了傳統方法中天向安裝角估計精度差的問題，能夠滿足車載導彈快速高精度初始對準的要求。

References)

［1］王丹丹，陳小軍，王麗華. 新對準技術應用展望［J］. 導彈與航天運載技術，2009(3):22 -23.WANG Dan-dan，CHEN Xiao-jun，WANG Li-hua. Outlook of new alignment technology applications［J］. Missile and Space Vechile，2009(3):22 -23.(in Chinese)

［2］周載學，傅正煊，胡憲文. 發射技術［M］. 北京:中國宇航出版社，2009:90 -120.ZHOU Zai-xue，FU Zheng-xuan，HU Xian-wen. Launch technology［M］. Beijing:China Astronautic Publishing House，2009:90 -120.(in Chinese)

［3］Xu Qing-jiu，Dai Hong-de，Wu Xiao-nan，et al. Design of simulation system about transfer alignment of SINS for shipborne equipment［C］∥2010 2nd International Conference on Information Science and Engineering. Hangzhou:IEEE，2010:4506 -4510.

［4］胡健，馬大為，程向紅，等. 基于Elman 網絡的傳遞對準容錯聯合濾波器設計與仿真［J］. 兵工學報，2010，31(11):1502 -1507.HU Jian，MA Da-wei，CHENG Xiang-hong，et al. Transfer alignment using fault-tolerant federated STF based on Elman network［J］. Acta Armamentarii，2010，31(11):1502 -1507.(in Chinese)

［5］Sun Chang-yue，Deng Zheng-long. Transfer alignment of shipborne inertial-guided weapon systems［J］. Journal of Systems Engineering and Electronics，2009，20(2):348 -353.

［6］Wang Ya-feng，Sun Fu-chun，Zhang You-an，et al. Central difference particle filter applied to transfer alignment for SINS on missiles［J］. Aerospace and Electronic Systems，2012，48(1):375 -387.

［7］王司，鄧正隆. 慣導系統動基座對準技術綜述［J］. 中國慣性技術學報，2003，11(2):61 -67.WANG Si，DENG Zheng-long. Technique review of transfer alignment of inertial navigation system on moving base［J］. Journal of Chinese Inertial Technology，2003，11(2):61 -67.(in Chinese)

［8］Shen Xiao-rong，Shi Yong-zhu. Angular rate matching method for shipboard transfer alignment based on H∞filter［C］∥2011 6th IEEE Conference on Industrial Electronics and Applications. Beijing:IEEE，2011:620 -625.

［9］韓鵬鑫，穆榮軍，崔乃剛. 兩種坐標系下慣導傳遞對準效果比較［J］. 中國慣性技術學報，2010，18(3):272 -278.HAN Peng-xin，MU Rong-jun，CUI Nai-gang. Comparison between transfer alignments of inertial navigation system in two coordinates［J］. Journal of Chinese Inertial Technology，2010，18(3):272 -278.(in Chinese)