面齒輪輪齒剛度計算方法研究

黃鵬，李政民卿

(南京航空航天大學 江蘇省精密與微細制造技術重點實驗室, 江蘇 南京 210016)

?

面齒輪輪齒剛度計算方法研究

黃鵬，李政民卿

(南京航空航天大學 江蘇省精密與微細制造技術重點實驗室, 江蘇 南京 210016)

摘要：基于Buckingham的觀點，將面齒輪齒形看作是由沿齒長方向一系列變壓力角的齒條組成，得到沿軸向和徑向都為變截面的面齒輪簡化齒形，獲得了面齒輪輪齒嚙合變形的計算公式，求解出了面齒輪的輪齒剛度。與有元法的分析結果進行比較，二者相對誤差較小，驗證了面齒輪輪齒剛度計算方法的可行性。

關鍵詞：面齒輪；輪齒變形；輪齒剛度；計算方法

面齒輪傳動是圓柱齒輪與面齒輪相嚙合的齒輪傳動，具有重合度大、無需防錯位設計、與面齒輪嚙合的直齒圓柱齒輪無軸向力作用和傳遞動力性能優越等優點[1,3]；據波音公司報道[4]，采用面齒輪傳動作為主減速器的阿帕奇Brock-Ⅲ型直升機已于2009年11月23日首飛成功。

在面齒輪傳動中，由面輪齒輪齒嚙合變形引起的剛度激勵是其傳動中的主要動態激勵之一，面齒輪傳動過程中的綜合嚙合剛度是研究動力學的基礎，而確定面齒輪輪齒剛度是研究面齒輪傳動綜合嚙合剛度的一項重要工作，因此有必要對面齒輪輪齒剛度的計算方法開展研究。

圓柱齒輪和圓錐齒輪嚙合剛度的計算和測量方法從20世紀就開始研究[5,6]，并取得了一定的研究成果。Isa Yesilyurt等人[7]對圓柱齒輪的單齒嚙合剛度的理論計算方法進行了研究，并采用模態法來測量圓柱齒輪的單齒剛度。而目前對于面齒輪輪齒剛度多采用有限元法計算得到，其計算效率低。本文對面齒輪輪齒剛度的解析計算方法進行研究，尋求一種高效準確的面齒輪輪齒剛度計算方法。

1 面齒輪齒形分析

基于Buckingham的觀點[8]：面齒輪齒形可以看作是沿齒長方向一系列變壓力角的齒條組成，如圖1(a)所示；其沿齒長方向上某一截面的齒形分析，如圖1(b)所示。

圖1　面齒輪齒形及齒形分析圖

根據圖1(b)中的幾何關系，可求出面齒輪嚙合半徑r2處的齒厚t[8]為：

t=2r1[(T/2R1)+invφ1-invφ]

(1)

式中：r1為漸開線直齒輪嚙合半徑；T為漸開線直齒輪在分度圓處的齒槽寬，其值為：

T=πm/2

其中：m為模數；R1為漸開線直齒輪分度圓半徑；φ為漸開線直齒輪壓力角；φ1為節點壓力角，其值為：

φ1=arccos(Rb/r1)

其中Rb為漸開線直齒輪基圓半徑。

齒條的齒頂高ha為：

ha=r1-Rr-c

(2)

式中：Rr為漸開線直齒輪齒根圓半徑；c為齒頂間隙。

齒條的齒根高hf為：

hf=Roc-r1

(3)

式中Roc為漸開線直齒輪齒頂圓半徑。

根據上述面齒輪齒形分析方法，以表1所列面齒輪參數在matlab中繪制無過渡圓弧的面齒輪單齒模型，如圖2所示。

表1　面齒輪傳動的齒輪副主要幾何設計參數

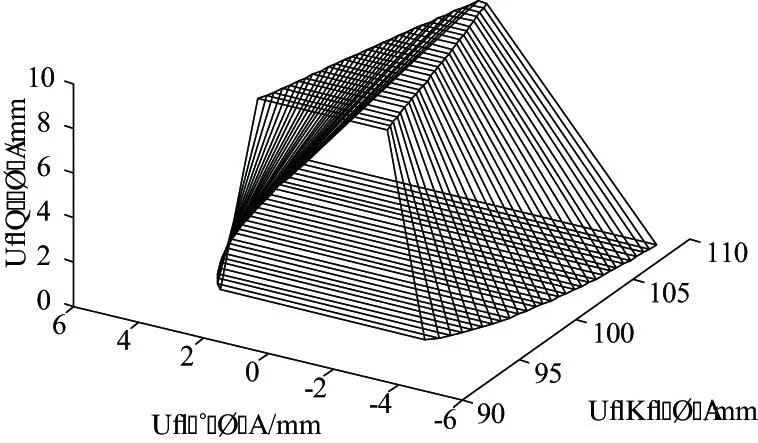
圖2　面齒輪單齒模型仿真圖

2面齒輪輪齒剛度計算方法

基于面齒輪的復雜齒形，在求解面齒輪輪齒剛度時需要對面齒輪齒形進行合理簡化。根據仿真圖2，可將面齒輪齒形簡化成由一系列沿齒高方向變化的梯形截面組成，如圖3所示。

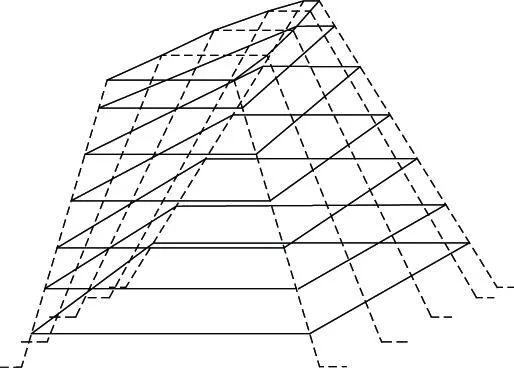
圖3　面齒輪單齒模型簡化示意圖

根據圖3中面齒輪齒形的簡化形式，其輪齒剛度的解析法求解思想仍然基于圓柱齒輪輪齒剛度的當量齒輪解析分析方法，即面齒輪的輪齒綜合彈性變形包括輪齒的彎曲變形、剪切變形、接觸變形以及由齒根基礎彈性傾斜引起的附加變形[9-11]。分析中，先通過求解輪齒各單一變形后，再將其相加，得出面齒輪輪齒在單位載荷作用下接觸點處的總變形量δf為：

δf=δ1+δ2+δ3+δ4

(4)

式中：δ1為彎曲變形；δ2為剪切變形；δ3為輪齒接觸變形；δ4為齒根基礎彈性傾斜引起的附加變形。

根據剛度和變形量-柔度的關系可知，面齒輪在接觸點處的輪齒剛度kf為:

kf=1/δf

(5)

2.1　面齒輪輪齒的彎曲變形和剪切變形

面齒輪輪齒的彎曲變形和剪切變形分析中，將在接觸范圍內的輪齒分成若干小段i，并把小段i看成一個懸臂梁，如圖4(a)所示；每個小段i沿齒長方向的截面可看作是隨面齒輪齒高方向變化的梯形截面，如圖4(b)所示。

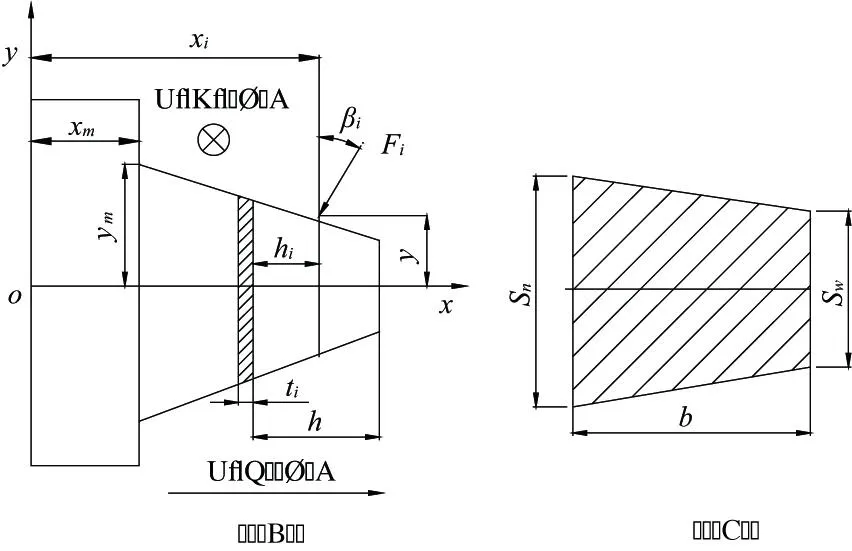
圖4　面齒輪輪齒簡化成的懸臂梁模型

根據截面上切應力的分布規律作以下2個假設[12]：

1) 橫截面上各點切應力的方向都平行于剪應力的方向；

2) 切應力沿截面寬度均勻分布。

根據上述假設，面齒輪輪齒在接觸點處的彎曲變形和剪切變形可通過對各小段的變形量求和獲得。

面齒輪輪齒在接觸點處彎曲變形包括單位長度載荷作用在小段i上產生的彎矩變形和橫向變形。

根據圖4(a)所示，取小段i的厚度為ti，截面面積為Ai，截面模量為Ii；小段i至載荷作用點沿x方向的距離為h，載荷作用點處的半齒厚為yi，齒根處的半齒厚為ym；泊松比為v，彈性模量為E；面齒輪齒寬為b；載荷與y軸間的夾角為βj；則單位長度載荷Fj作用在小段i上的彎矩變形δ11為：

(6)

由Fj對小段i產生的橫向變形δ12為：

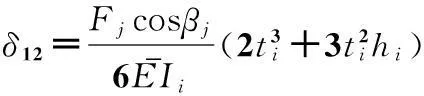
(7)

因此，單位載荷作用下小段i的彎曲變形δbi為：

δbi=δ11+δ12

(8)

由Fj對小段i產生的剪切變形δsi為：

(9)

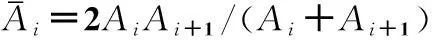
根據圖4(b)可知，由于各小段的截面均是隨面齒輪齒高位置變化的梯形截面，因此其截面模量Ii為：

(10)

截面面積Ai為：

Ai=b(Sn+Sw)/2

(11)

式中，沿齒高方向任意高度h處的Sn、Sw可采用圖5所示模型計算。

圖5　Sn，Sw的計算模型

根據圖5可知，利用梯形ABCD可求得:

Sn=d1+2(h-a1)tanφmin

(12)

式中：φmin為面齒輪內半徑節線處的壓力角；d1為面齒輪內半徑節線處的齒厚；a1為面齒輪內半徑節線位置到齒頂的距離。d1和a1的計算式分別為：

d1=2r11(T/2R1-invφmin+invφ)

a1=r11-Rr-c

式中r11為面齒輪內半徑。

利用梯形EFGH可求得:

Sw=d2+2(h-a2)tanφmax

(13)

式中：φmax為面齒輪外半徑節線處的壓力角；d2為面齒輪外半徑節線處的齒厚；a2為面齒輪外半徑節線位置到齒頂的距離。d2和a2的計算式分別為:

d2=2r12(T/2R1-invφmax+invφ)

a2=r12-Rr-c

式中r12為面齒輪外半徑。

利用式(8)-式(13)，可分別求出面齒輪輪齒在載荷作用點處沿載荷方向的彎曲變形和剪切變形，其中彎曲變形δ1為:

(14)

剪切變形δ2為:

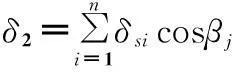
(15)

式中n為小段i的個數。

2.2　面齒輪輪齒接觸變形和齒根基礎彈性傾斜引起的附加變形

面齒輪接觸變形分析是以布希涅斯克問題的解為基礎，根據物體表面上有相同距離的點在公切面上形成類橢圓區域的結論，得出面齒輪輪齒的接觸變形δ3[13]為：

(16)

式中：J為橢圓積分系數，可通過查橢圓積分系數表獲得；ρx為接觸區域橢圓長半徑，θg和θf可由下式確定：

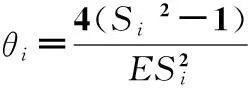
(17)

其中：i分別為g和f；Si為材料縱向延伸和橫向壓縮比的系數；E為材料的彈性模量。

面齒輪齒根基礎彈性傾斜引起的附加變形δ4[14-15]為：

(18)

式中：Lf=xj-xm-yjtanβj，Hf=2ym。

3輪齒剛度解析法的可行性驗證

為驗證上述面齒輪輪齒剛度計算方法的可行性，將解析法計算結果與有限元法計算結果進行對比分析。根據表1中所列面齒輪參數，建立面齒輪有限元分析模型，如圖6所示。

圖6　面齒輪有限元分析模型

利用圖6中模型，將計算得到的變形量轉換為輪齒剛度并與上述面齒輪輪齒剛度解析計算方法進行比較，如表2所示。

表2　解析法與有限元法的剛度計算比較表

采用有限元法和本文介紹的方法計算得到的面齒輪輪齒變形量及輪齒剛度沿齒高方向變化的曲線分別如圖7(a)和圖7(b)所示。

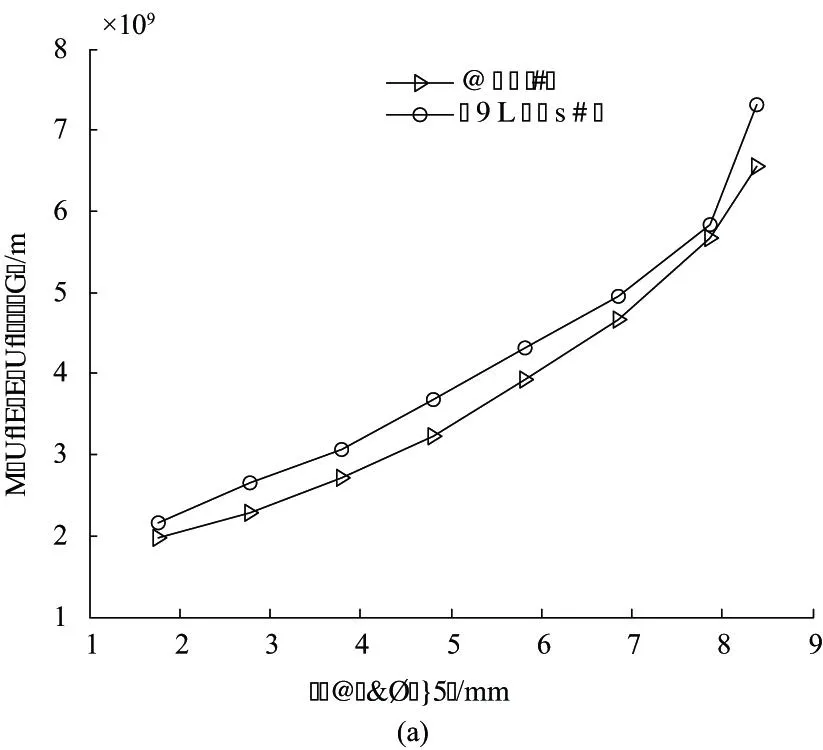
圖7　解析法與有限元法計算結果對比

根據圖7可知，解析法計算的面齒輪輪齒嚙合變形及輪齒剛度與有限元法分析所得結果相差較小。為進一步分析面齒輪剛度解析法的可行性，定義解析法與有限元法的相對平均偏差η為:

(19)

式(19)中，N為接觸點個數。利用式(19)對表2中數據分析可知，解析法與有限元法的相對平均偏差為10.32%。因此，上述面齒輪輪齒剛度的解析計算方法是可行的。

4結論

1) 基于Buckingham的觀點，將面齒輪齒形看成是由一系列變壓力角齒條組成，形成了用于求解面齒輪輪齒剛度的齒形建模方法。

2) 將無過渡圓弧的面齒輪齒形看作是沿軸向和徑向均為變截面的梯形彈性懸臂梁，運用材料力學方法，形成了面齒輪輪齒剛度的解析計算方法。

3) 分別運用解析法和有限元法計算出了面齒輪輪齒剛度，得到了輪齒剛度沿齒高方向的變化規律，兩種計算方法得到的結果相差很小，證明了面齒輪輪齒剛度的計算方法的可行性。

參考文獻:

[1] LITVIN F L, WANG J C, BOSSLER R B Application of face gear drives in helicopter transmissions [J]. Journal of Mechanical Design, Transactions of the ASME, 1994, 116 (3) : 672～676.

[2] HANDSCHUH R F, LEWICKI D G, BOSSLER R B. Experimental testing of prototype face gears for helicopter transmissions [J]. Journal of Aerospace Engineering, 1994, 208 (2) : 129～136.

[3] BILL R C. Summary highlights of the advanced rotorcraft transmission (ART) program [R]. American Inst of Aeronautics and Astronautics, New York, 1992.

[4] MESA Ariz. Boeing AH-64D Apache Block III structures test aircraft makes 1st flight [EB/OL]. [2009-12-4]. http://boeing.mediaroom.com/index.php?s=20295&item=977.

[5] MONSAK P, KAZEM K. Efficient evaluation of spur gear tooth mesh load using pseudo-interference stiffness estimation method [J]. Mechanism and Machine Theory. 2002, 37(8): 769~786.

[6] COMELL R W. Compliance and stress sensitivity of spur gear teeth [J]. Journal of Mechanical Design, 1981,103: 447~459.

[7] ISA Y, GU F, ANDREW D B. Gear tooth stiffness reduction measurement using modal analysis and its use in wear fault severity assessment of spur gears [J]. NDT&E International 2003,36 (5) :357~372.

[8] BUCKINGHAM E. Analytical mechanics of gears [M]. New York, Dover Publications, 1949: 302~320.

[9] BAND R V，PETERSON R E. Load and stress cycle in gear teeth [J]．Mechanical Engineering，1929，51(9)：653～662.

[10] WEBER C．The deformation of loaded gears and the effect on their load carrying capacity [J]．Sponsored Research (Germany) ，British Dept．of Scientific and Industrial Research，Report，1949 (3).

[11] ATTIA A Y． Deflection of spur gear teeth cut in thin rims [J]．ASME Eng. Ind，1964，86(4)： 333~341.

[12] 劉鴻文．材料力學[M]. 北京：高等教育出版社，2004.

[13] 李政民卿，朱如鵬．面齒輪傳動的承載接觸分析[J]．南京航空航天大學學報，2010，42(2)：219~223.

[14] 吳俊飛，郭建章．變厚齒輪輪齒嚙合綜合剛度確定方法研究[J]．青島化工學院學報，2002，23(1)：74~76.

[15] 李潤方，王建軍.齒輪系統動力學-振動、沖擊、噪聲[M]．北京：科學出版社，1996.

Research on Method of Calculating Stiffness of Face Gear Tooth

HUANG Peng，LI ZHENG min-qing

( Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology,

Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:Based on Buckingham’s standpoint, along the length of the tooth of face gear , any one of its sections can be considered as a section of rack with varying pressure angle. According to above theory, the tooth form of the face gear is simulated successfully. The calculating method of the tooth’s stiffness of the face gear is obtained. Compared with the result of analyzing the tooth’s stiffness by FEM, both relative errors are almost same. it is proved that the calculation method for its stiffness is correct.

Keywords:face gear; gear tooth deformation; gear tooth stiffness; calculating method

中圖分類號：TH132.429

文獻標志碼：A

文章編號：1671-5276(2015)02-0046-04

作者簡介：黃鵬(1987-)，男，湖北隨州人，碩士研究生，主要從事機械傳動與減振降噪研究。

基金項目：國家自然科學基金(51105194)；國家留學基金資助(201206835011)

收稿日期：2014-11-08