基于偏度與峰度的數據質量評估

崔書華,李 果,劉軍虎,宋衛紅,沈 思

(1 宇航動力學國家重點實驗室,西安 710043;2 西安衛星測控中心,西安 710043)

?

基于偏度與峰度的數據質量評估

崔書華1,2,李 果2,劉軍虎2,宋衛紅2,沈 思2

(1 宇航動力學國家重點實驗室,西安 710043;2 西安衛星測控中心,西安 710043)

針對外彈道測量數據質量情況,拓展數據質量評價標準,提出了用分布偏度與峰度的分析方法描述數據質量狀態。通過對跟蹤測量數據進行分析驗證,證明運用該方法可有效、直觀的定量、定性的確定數據質量情況,為跟蹤測量數據的使用提供了可靠性評價及使用決策。

偏度;峰度;數據分析;結果評估

0 引言

正態分布是外彈道測量數據質量分析最常使用的理論基礎,通常也是統計測量數據隨機誤差的前提。所以,正態分布的檢驗在外彈道數據處理中是關鍵環節。檢驗一個樣本是否服從正態分布的方法有很多,包括Kolmogorov檢驗、χ2擬合優度檢驗、Shapiro-Will檢驗和偏度-峰度檢驗等。但各有一些局限性，如Kolmogorov檢驗只有當假設的分布完全已知的時候才適用，χ2檢驗犯第二類錯誤(接受不正確零假設的錯誤)的概率往往較大，Shapiro-Will檢驗要求樣本容量不大于50[1]等。而偏度-峰度法是一種快速、有效的正態檢驗方法，并且對樣本的容量沒有嚴格要求。現有文獻中，在其他領域有較多的利用偏度-峰度法對數據進行分析、判斷、決策，如文獻[2-6]闡述了在各自的領域充分利用偏度-峰度技術取得的成果，但在外彈道測量數據質量分布的偏度和峰度分析方面極少。因此,文中選用偏度-峰度檢驗法對外彈道測量數據進行分析,通過偏度和峰度統計量檢驗樣本是否服從先前的假設條件,以期更為客觀地反映實測數據情況,并給出飛行目標彈道計算結果的可靠性評價及使用建議,為彈道的最優化連接和數據融合中的權值最優匹配做出決策。

1 方法介紹

在外彈道數據處理中,最典型的擬合方法就是利用最小二乘原理求解,即要求各數據偏離曲線函數值的誤差的平方和最小。它通過最小化誤差平方和找到一組數據的最佳函數匹配。通過擬合之后,獲取隨機變量,隨機變量的三階中心矩成為偏度,隨機變量的四階中心矩成為峰度。偏度和峰度是描述分布形狀的重要數字特征。

1.1 偏度檢驗

偏度(skewness)是統計隨機變量數據分布偏斜方向和程度的度量,是統計隨機變量數據分布非對稱的數字特征。偏度是利用三階矩定義的,其物理含義為:

設x1,x2,…,xn是來自總體x的一個樣本,則總體x的偏度可估計為:

(1)

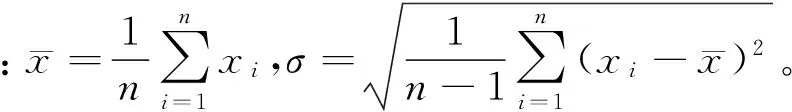
若s>0,則稱x的分布是正偏(或右偏),意味著在概率密度函數右側的尾部比左側長,絕大部分值位于平均值的左側;若s<0,則稱x的分布是負偏(或左偏),意味著在概率密度函數左側的尾部比右側長,絕大多數的值位于平均值的右側;若s=0,則表示數值相對均勻的分布在平均值的兩側。|s|越大,說明分布偏斜得越厲害。對偏度值影響較大的是分布在其中一個方向上的尾部有拉長趨勢的程度[4]。

1.2 峰度檢驗

峰度(kurtosis)是另一個反映隨機變量分布形狀的量,其是利用四階矩定義的,物理含義為:

設x1,x2,…,xn是一組樣本數據或一組有限總體數據,則其峰度的計算公式為:

(2)

峰度度量的是好數據的集中程度,峰度的取值范圍是[-3,∞],正態峰度分布時為k=0,表示好壞數據差距處于一個合適的“度”;若k<0,則說明x分布尾部比正態分布的尾部細,表示好數據比較分散,好壞數據差距大,且|k|越大,尾部越細；若k>0,則說明隨機變量x分布的尾部比正態分布的尾部粗,表示好數據比較集中,好壞數據差距小,并且k值越大,尾部越粗;若k為無窮大時,好壞數據沒有差距,曲線變成一條直線。峰度可以用來比較已標準化了的各隨機變量分布的尾部厚度。

1.3 檢驗方法

單純利用偏度或單純利用峰度來分析數據的分布情況是有缺陷的,只有兩者同時進行檢驗才能保證對數據進行客觀評價。即當s=0且k=0時,數據才能滿足正態分布。但值得關注的是,數據的偏度和峰度在什么數值范圍內才能認為數據分布可作正態近似,這很難給出一般性的答案[5]。所以,在外彈道測量數據進行綜合分析時需要對隨機誤差數據同時進行偏度和峰度的檢驗,在確定數據融合的使用跟蹤弧段時,需要綜合考慮其他跟蹤測量設備的數據情況,通過比對分析同跟蹤弧段不同設備隨機誤差數據的偏度和峰度檢驗結果,確定最優權值的匹配,以期達到逼近實際目標飛行的彈道參數。

2 實例分析

以雷達跟蹤測量數據為例(這里假設雷達測量數據已對系統誤差進行了充分、可靠的修正),綜合討論其從測元數據到最終結果的質量情況,以及彈道高可信度選擇及可使用弧段的確定。

2.1 擬合殘差分析

圖1～圖3為某雷達跟蹤測量數據的測距R、俯仰角E和方位角A數據應用最小二乘方法擬合后與原始測量數據的殘差數據圖。

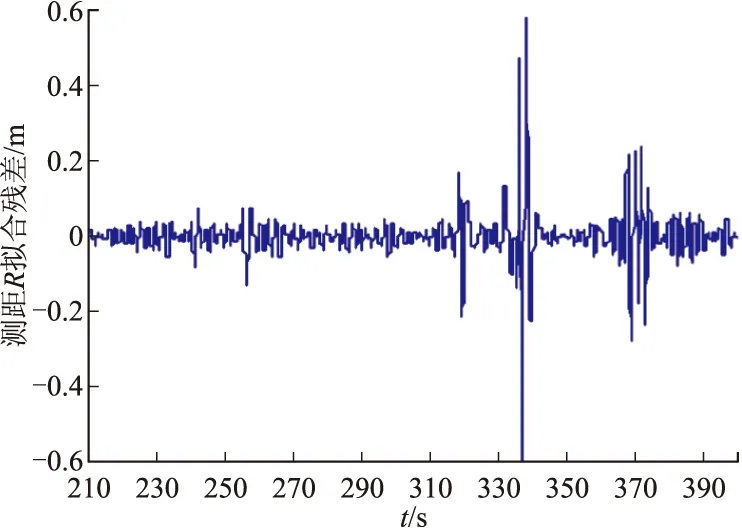
圖1 測距R擬合差殘數據圖

圖2 俯仰角E擬合殘差數據圖

圖3 方位角A擬合殘差數據圖

從圖1～圖3可以直觀地看出,某些弧段跟蹤測量的數據擬合殘差較好。但是,如果定量的確定哪些跟蹤測量數據可以滿足正態分布的前提假設,并確定是否具有高的可使用度,還必須進一步進行分析。在下面的討論中,將針對3個測元的跟蹤測量弧段280～310 s的數據進行相關分析。

2.2 偏度峰度分析

圖4～圖6為雷達跟蹤測量數據測距R、俯仰角E和方位角A數據隨機差相對應的偏度與峰度統計數據圖。

圖4 測距R偏度及峰度數據圖

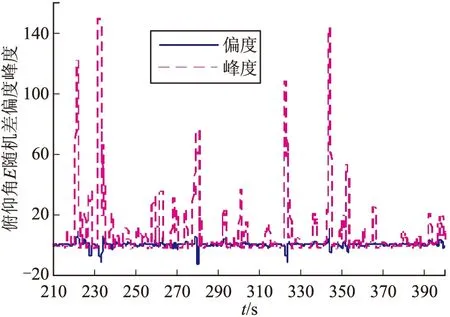
圖5 俯仰角E偏度及峰度數據圖

圖6 方位角A偏度及峰度數據圖

從圖4～圖6中可以看出,測距R的隨機差數據的偏度和峰度在280～310 s弧段量值適度,其相對應弧段的方位角A隨機誤差的偏度和峰度也較其他弧段適度。為了便于飛行器目標定位精度情況的分析,選取具有相對較好偏度與峰度量值的280～310 s俯仰角E數據。

2.3 目標位置精度分析

上述分析的雷達跟蹤測量的數據質量情況,為確定高可信度的使用弧段奠定了基礎。為了行文方便,這里簡單介紹單臺雷達跟蹤測量數據定位精度計算方法,式(3)為飛行器目標位置精度計算公式。

(3)

式中:R、E、A分別為測距、俯仰角和方位角的跟蹤測量數據;σR、σE、σA分別為測距、俯仰角和方位角隨機誤差統計精度數據。

圖7～圖9為雷達跟蹤測量數據單臺定位后,飛行器目標在3個方向的位置精度數據圖。

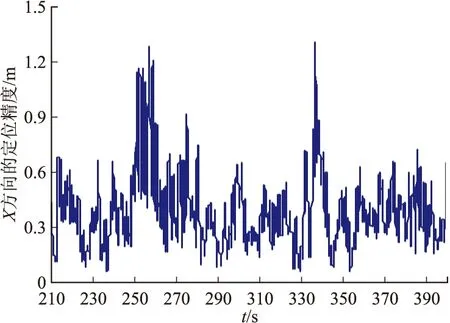
圖7 目標在X方向的位置精度數據圖

圖8 目標在Y方向的位置精度數據圖

圖9 目標在Z方向的位置精度數據圖從圖7～圖9精度數據來看,結合偏度-峰度的統計結果,可信度高的使用段應為280～310 s。相對來講,雖然飛行目標在

Y

方向的210～250 s之間的定位精度較高,但結合式(3)和測距

R

的偏度與峰度綜合考慮,此段的樣本偏度有明顯的左偏和右偏情況,同時也處在多峰的數據弧段,故此段數據可信度不如280～310 s的數據。

3 結論

通過上述分析可知,當跟蹤測量數據的隨機誤差樣本嚴重左偏、嚴重右偏、多峰或其他非正態分布,即檢驗樣本不服從先前的假設條件時,會使目標的定位誤差很大。只有綜合考慮跟蹤測量數據的偏度和峰度,才能準確判定數據的可使用跟蹤弧段。所以,利用偏度-峰度的分析手段,不僅可以判斷數據處理的可信區域,也能為獲得更準確的定位精度尋求一種合理、科學、有效的手段。文中為外彈道測量數據評價與分析的方法,以及為后續彈道的數據融合和彈道連接提供了參考。

[1] 宋震龍, 將剛毅, 黃晃, 等. 基于偏度-峰度檢驗的無線局域網室內定位算法 [J]. 通信學報, 2012, 33(5): 99-105.

[2] 傅俊輝, 張衛國, 陸倩, 等. 考慮偏度風險和峰度風險的非線性期貨套期保值模型 [J]. 系統工程, 2009, 27(10): 44-48.

[3] 王春峰, 莊泓剛, 房振明, 等. 多維條件方差偏度峰度建模 [J]. 系統工程理論與實踐, 2010, 30(2): 324-331.

[4] 王學民. 偏度和峰度概念的認識誤區 [J]. 統計與決策, 2008, 264(12): 145-146.

[5] 王學民. 關于樣本均值的抽樣分布能否作正態近似的探討 [J]. 統計研究, 2005(7): 75-77.

Assessment and Analysis of Trajectory Measurement Data Based onSkewness and Kurtosis

CUI Shuhua1,2,LI Guo2,LIU Junhu2,SONG Weihong2,SHEN Si2

(1 State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China; 2 Xi’an Satellite Monitor and Control Center, Xi’an 710043, China)

Due to quality of trajectory measurement data and extension of quality standard, distributed skewness and kurtosis analysis were put forward. It is proved that application of the method is able to determine quantitative and qualitative quality of data effectively and directly by analysis and verification of measurement data. Also, the method provides reliability evaluation and suggestion on measurement data.

skewness; kurtosis; data analysis; assessment of results

2014-12-17

國家自然科學基金(61473222;61231018;41274018)資助

崔書華(1964-),女,天津人,高級工程師,研究方向:外彈道數據處理方法及評估。

V557

A