一種光雷組合測量求取高精度彈丸切向速度方法

宮志華,劉志學,冷雪冰,董立濤,徐 旭,段鵬偉

(中國白城兵器試驗中心,吉林白城 137000)

?

一種光雷組合測量求取高精度彈丸切向速度方法

宮志華,劉志學,冷雪冰,董立濤,徐 旭,段鵬偉

(中國白城兵器試驗中心,吉林白城 137000)

彈丸切向速度在彈道學領域內是一個重要的技術參數。為獲取高精度切向速度參數,提出一種基于測速雷達和光學經緯儀合理布站優化組合測量與數學計算求取的方法,在利用高質量雷達徑向速度測元和經緯儀角度測元的基礎上,再輔以數學壓噪的方法,能夠求取高精度的彈丸切向速度參數。仿真計算結果表明,該方法具有彈丸切向速度求取精度高、計算效率好和工程應用簡潔的顯著特點。

兵器科學與技術;切向速度;測速雷達;光學經緯儀;聯合測量;函數擬合

0 引言

在武器系統試驗鑒定中,彈丸切向速度是一個重要的技術參數,無論對于分析運動目標的飛行穩定性、辨識目標的氣動力系數和射表編擬都具有關鍵作用[1]。彈丸切向速度是指彈道切向速度,也稱彈道速度[2]。由測速雷達測量得到的速度測元是彈丸相對于雷達的徑向運動速度,雖然具有很高的測量精度[3],但其不是彈丸切向速度,而是切向速度在雷達徑向上的投影分量,必須經幾何變換才能得到切向速度。可見,彈丸切向速度是一個三維矢量,無法由某種測量設備的獨立測元來唯一決定,因此,需要不同測元組合計算求取。如果不能有效的抑制測元測量誤差,則這種組合計算方法會給切向速度的求取帶來很大的傳遞誤差。即使由組合測量獲得很高精度的彈丸坐標數據,直接利用坐標微分求取彈丸切向速度的方法,還是會受到隨機誤差和采樣頻率的影響[4-5],仍然無法滿足彈丸切向速度的高精度測量要求。針對這些問題,文中提出一種基于測速雷達和光學經緯儀合理布站優化組合測量與數學計算求取的方法,并對該方法進行了仿真驗證分析,得出了可靠結論。

1 測量與計算模型

選用1部測速雷達設備和1臺(或2臺)光學經緯儀設備組成聯合測量系統。根據設備測量特性,將測速雷達布設在彈丸運動軌跡初始前方,光學經緯儀布站在彈丸運動軌跡側方。利用測速雷達提供的高質量徑向速度測元v數據和光學經緯儀提供的高質量角度測元(方位角α和俯仰角θ)數據進行組合計算,求解彈丸切向速度。

為抑制各測元隨機誤差影響,考慮對彈道坐標參數(x,z,y)進行函數擬合。其中,要求擬合函數必須能對較長的非平穩運動目標軌跡進行精確的逼近,即截斷誤差小[6-8]。選用三次Hermite函數表征[9],如式(1)所示。

(1)

(2)

為書寫簡潔,省去(x,z,y)下標,式中:

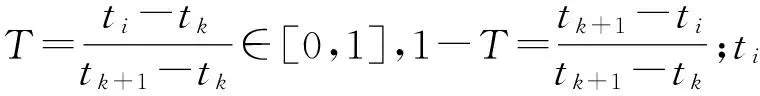
由式(2)可得彈丸切向速度:

(3)

由于徑向速度測元、方位角測元和俯仰角測元與彈道坐標參數均為非線性函數關系,則以式(1)、式(2)為基函數表征徑向速度、方位角和俯仰角這三種測元,并按泰勒級數展開轉化為線性方程后組成的聯合誤差方程如式(4)所示。

(4)

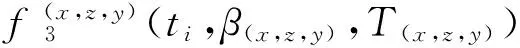
將式(4)寫成矩陣形式為:

ξ=HX+η

(5)

式中:ξ為由3個測元殘差(eαi,eθi,ev)組成的誤差向量;H為Hermite擬合函數系數(βx,βz,βy)表征各測元的設計矩陣;X為由Hermite擬合函數系數(βx,βz,βy)組成的待估參數向量;η為各測元常數向量。在已知Hermite擬合函數節點分布的前提下,依據最小二乘法原理對式(5)進行解算,可以得到與Hermite擬合系統相關的待估參數解為:

(6)

式中:P為權值矩陣。以測元統計隨機誤差方差比為依據設計為對角矩陣。

當有2臺以上光學經緯儀參與聯合測量時,參與計算的測元數量(>3)已經出現冗余,這時還可以考慮在方程(4)中加入測元系統誤差模型,寫成矩陣形式為:

ξ=HX+BC+η

(7)

式中:B表示與測元系統誤差模型相關的設計矩陣;C表示與測元系統誤差模型相關的待估參數。

同理,依據最小二乘法原理對式(7)進行解算,可得與Hermite擬合系統和系統誤差模型系數相關的待估參數解為:

[XT,CT]T=-([A,B]TP[A,B])-1[A,B]TPη

(8)

在實際求解中,為獲得合適的節點分布,可針對運動目標加速度變化特點來選取[6,10],即在加速度變化劇烈的時段,采用較密的節點分布,在加速度變化平穩的時段,采用稀疏節點分布;另由于非線性函數級數展開和初始目標軌跡參數的近似性共同帶來的截斷誤差,需對式(5)或(7)進行迭代計算。將最終解算得到的Hermite函數擬合系數代入式(2)中,即可由式(3)獲得彈丸切向速度參數。

2 仿真驗證

首先,在發射坐標系下,依據質點運動方程推算一條彈丸理論彈道坐標數據和切向速度數據作為真值。選取1部測速雷達和2臺光學經緯儀,對其測元數據進行仿真設計。首先,確定設備站址分布,雷達、經緯儀站址和彈丸運動軌跡的幾何關系如圖1所示。

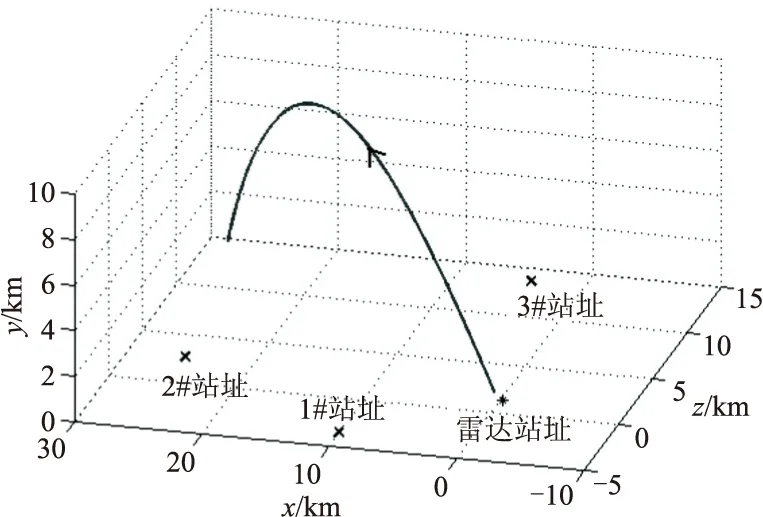
圖1 設備站址與彈道軌跡空間幾何關系

以理論彈道坐標為基準,反推產生1部測速雷達的1個徑向速度測元數據和2臺光學經緯儀(1站和2站)的4個角度測元數據,并結合設備工程應用經驗,給這5個仿真測元分別加入合理的隨機誤差和系統誤差,具體數值見表1。仿真彈丸的徑向速度和切向速度曲線如圖2所示。初值設計為在理論彈道坐標參數(x,z,y)真值的基礎上分別加上800 m、1 000 m、700 m的固定誤差和6 m、6 m、8 m的隨機誤差。

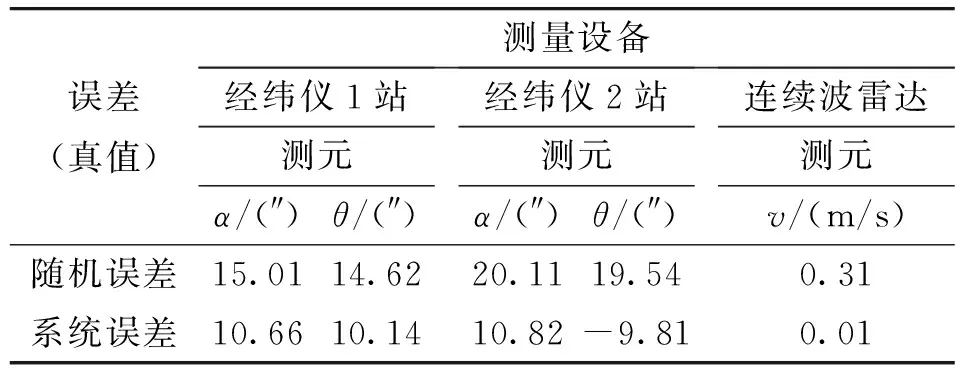
表1 測量設備仿真測元加入誤差值情況

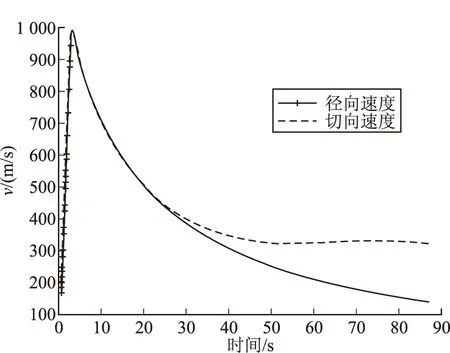
圖2 彈丸徑向速度和切向速度仿真數據曲線

與分析問題有關,2臺光學經緯儀可分別布設在3個站址上,其中,1臺經緯儀布設在1#站址上,另一臺經緯儀布設在2#站址或3#站址上。

根據設備站址分布,共確定4套聯合測量方案進行分析,分別是:第1套方案,采用1部測速雷達和1臺光學經緯儀組成聯合測量系統,其中,光學經緯儀布設在1#站址上;第2套方案,采用1部測速雷達和1臺光學經緯儀組成聯合測量系統,其中,光學經緯儀布設在3#站址上;第3套方案,采用1部測速雷達和2臺光學經緯儀組成聯合測量系統,其中,2臺光學經緯儀分別布設在1#站址和2#站址上;第4套方案,采用1部測速雷達和2臺光學經緯儀組成聯合測量系統,其中,2臺光學經緯儀分別布設在1#站址和3#站址上。

從上述分析可以知道,在實際計算中,采用Hermite函數對彈道坐標參數(x,z,y)進行表征,需要事先確定函數節點分布。依據彈丸運動加速度曲線變化情況,如圖3所示,在前4 s時段內彈丸運動加速度變化劇烈,采用較密節點分布,后續時段中,彈丸運動加速度變化平穩,采用較稀疏節點分布。

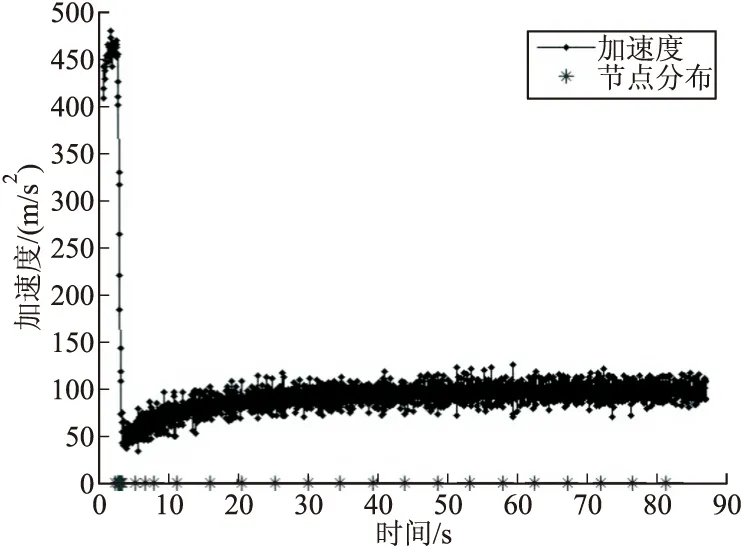
圖3 彈丸加速度曲線和擬合函數節點分布

在確定了Hermite函數自由節點分布的基礎上,采用上述方法結合以上4種測量方案分別對彈丸切向速度進行計算求取,并分析計算精度。經過計算,第1套方案解算的彈丸切向速度與真值比對誤差曲線如圖4所示。4種方案解算運動目標切向速度的誤差統計結果見表2。

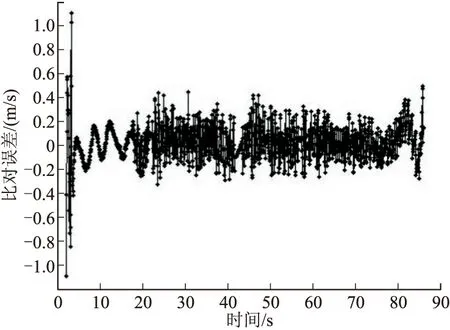
圖4 第1套方案求取切向速度與真值比對誤差曲線

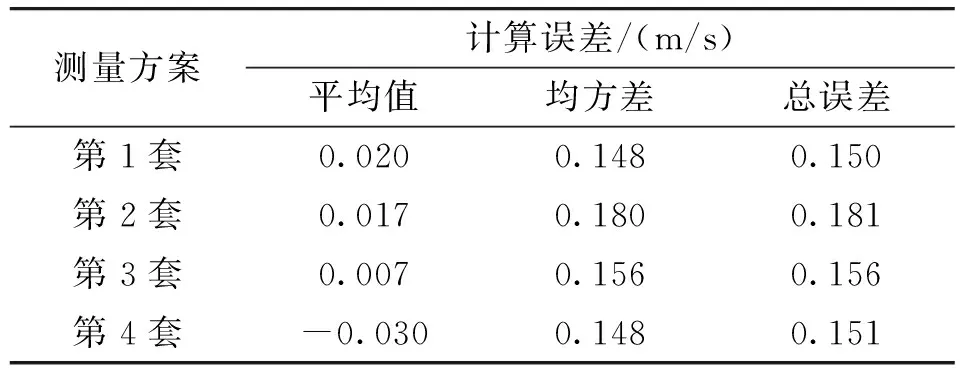
表2 4套測量方案求取切向速度誤差統計

從圖4和表2可以看到,針對仿真數據,設計的4種測量方案計算獲取的切向速度總誤差都不超過0.2 m/s,在加速度變化劇烈的時段,誤差變化比較大;只有1臺光學經緯儀參與的聯合測量和計算獲得切向速度,方案2的精度低于方案1,說明設備布站幾何關系對精度具有很大影響;在不考慮測元系統誤差的前提下,2臺光學經緯儀參與的聯合測量和計算求取的切向速度精度并沒有比只有1臺光學經緯儀參與的聯合測量和計算獲得切向速度精度高。

因為第3套和第4套測量方案出現測元數量冗余情況,則考慮測元系統誤差后,求取切向速度誤差統計結果如表3所示。

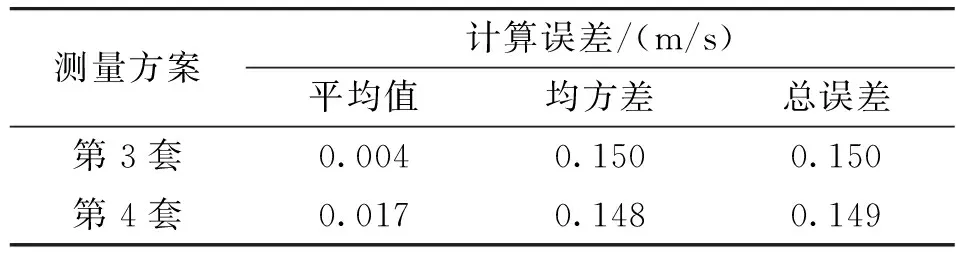
表3 冗余測量方案求取切向速度誤差統計

結果顯示,切向速度誤差減小,但與第1套測量方案比較,誤差較小幅度并不顯著。因此,從仿真分析來看,采用第1套測量方案是一種比較實用的方法,不僅切向速度求取精度高,而且工程應用簡潔。

3 結論

1)采用測速雷達和光學經緯儀組合測量方法,運用函數表征彈道坐標參數的數學壓噪計算方法,可以獲得高精度的彈丸切向速度,計算結果有效證實了這種方法的正確性。

2)在只有1部測速雷達和1臺光學經緯儀組成聯合測量的基礎上,布站幾何關系對計算精度有較大影響;增加光學經緯儀數量,在布站幾何關系較好的前提下,在不考慮測元系統誤差的情況下,并不絕對提高彈丸切向速度精度,但可以對切向速度計算精度起到很好的穩定作用;在考慮系統誤差的情況下,求取的切向速度精度并沒有大幅度提高。

3)對于加速度變化比較劇烈的運動目標段,為提高切向速度求取精度,應適當提高測量設備原始測元的采樣率,以進一步提高擬合函數表征彈道坐標參數的準確性,提高噪聲壓制質量,降低截斷誤差。

[1] 閆章更, 祁載康. 射表技術 [M]. 北京: 國防工業出版社, 2000.

[2] 周旦紅, 楊莘元, 楊楠. 多普勒測速雷達速度轉換的誤差分析 [J]. 哈爾濱工程大學學報, 2007, 28(1): 93-96.

[3] 宮志華, 段鵬偉, 董立濤. 運動目標測量雷達極限精度分析與仿真 [J]. 現代雷達, 2012, 34(6): 74-77.

[4] 郭文勝, 宮志華, 董立濤, 等. 雷達測距擬合微分求速方法研究 [J]. 現代雷達, 2010, 32(8): 33-38.

[5] 王正明, 易東云, 周海銀. 彈道跟蹤數據的校準與評估 [M]. 長沙: 國防科技大學出版社, 1999.

[6] 朱炬波. 不完全測量數據建模與應用 [D]. 長沙: 國防科學技術大學, 2004.

[7] 劉利生, 李杰. 外測數據事后處理 [M]. 北京: 國防工業出版社, 2000.

[8] 郭軍海. 彈道測量數據融合技術 [M]. 北京: 國防工業出版社社, 2012.

[9] 詹武平, 諶廷政, 劉成, 等. 組網雷達測量色噪聲數據的Hermite插值融合方法 [J]. 現代雷達, 2012, 34(6): 41-44.

[10] 賈興權. 連續波雷達數據處理 [M]. 北京: 國防工業出版社, 2005.

A Method of Getting High Precision Ballistic Tangential VelocityBased on United Measuring with Optical Theodolite and Radar

GONG Zhihua,LIU Zhixue,LENG Xuebing,DONG Litao,XU Xu,DUAN Pengwei

(Baicheng Ordnance Test Center of China, Jilin Baicheng 137000, China)

Ballistic tangential velocity is an important technical parameter in ballistics. To get high precision tangential velocity, a new method based on united measuring and mathematic calculation with optimized distributed speed measuring radar and optical theodolite was proposed High precision tangential velocity can be calculated by high quality radial velocity measuring element of radar and angle measuring element of optical theodolite with noise attenuation method. The simulation results show that, the new method could get high precision ballistic tangential velocity; also it is efficient and concise in engineering application.

ordnance science and technology; tangential velocity; speed measuring radar; optical theodolite; united measuring; function fitting

2014-12-06

總裝青年科技基金資助

宮志華(1975-),男,遼寧盤錦人,高級工程師,碩士,研究方向:外彈道數據融合處理和雷達信號處理。

TN959

A