基于實測電力噪聲分布的窄帶電力噪聲建模

谷志茹，劉宏立?，譚周文，劉述鋼

(1．湖南大學(xué) 電氣與信息工程學(xué)院，湖南 長沙 410082;2．湖南科技大學(xué) 物電學(xué)院，湖南 湘潭 519000)

基于實測電力噪聲分布的窄帶電力噪聲建模

谷志茹1，劉宏立1?，譚周文1，劉述鋼2

(1．湖南大學(xué) 電氣與信息工程學(xué)院，湖南 長沙 410082;2．湖南科技大學(xué) 物電學(xué)院，湖南 湘潭 519000)

基于實際測量電力噪聲特性參數(shù)的統(tǒng)計分布，推導(dǎo)非高斯分布的窄帶電力噪聲模型，主要包括背景噪聲和脈沖噪聲.前者應(yīng)用升余弦滾降濾波法建模，其功率服從正態(tài)分布；后者利用隨機(jī)分布的特性參數(shù)：脈沖的寬度、間隔和包絡(luò)所構(gòu)建的脈沖函數(shù)來建模.寬度、間隔和包絡(luò)隨機(jī)量均服從分隔馬氏鏈.然后應(yīng)用實際測量數(shù)據(jù)和馬爾克夫鏈蒙特卡羅(Markov Chain Monte Carlo, MCMC)分析法比較評估了此模型，數(shù)值分析結(jié)果顯示，模型能夠很好地逼近實際的電力噪聲.

電力線通信; 智能電網(wǎng); 正交頻分復(fù)用；分隔馬氏鏈；馬爾克夫鏈蒙特卡羅

基于電力信道的通信技術(shù)是智能電網(wǎng)(Smart Grid)建設(shè)的主要通信方式.它不需要重新鋪設(shè)專用的通信通路，通過在與傳遞電能同一路徑的線路上確定通信鏈路來傳遞信息，并且電力線通信不會像無線通信那樣容易被密集的建筑物所阻擋，從而減少安裝和維護(hù)費用.電力線通信技術(shù)市場長期被單載波PLC技術(shù)所壟斷.最近，被稱為G3和PRIME標(biāo)準(zhǔn)[1]的OFDM窄帶(10～95 kHz) PLC技術(shù)進(jìn)入了市場.它提供高的通信速率，魯棒的通信模式，這些是智能電網(wǎng)雙向通信的關(guān)鍵.但是，作為信息傳輸媒介來進(jìn)行數(shù)據(jù)或語音傳輸，低壓配電網(wǎng)絡(luò)具有負(fù)荷情況復(fù)雜、信號衰減大，信道容量小，并存在背景噪聲、隨機(jī)脈沖噪聲、與工頻同步的諧波噪聲等.所以為滿足智能電網(wǎng)雙向通信的需求，以電力網(wǎng)絡(luò)為信道的高速通信技術(shù)，必須有適應(yīng)于電力信道的調(diào)制和編碼方案，能夠抵抗惡劣的信道屬性等等，這都需要對實際電力線信道有深入的了解.

電力信道中影響高速通信的主要因素有因電纜損耗導(dǎo)致的信號衰減、多徑傳播和噪聲等.其中多徑傳播在文獻(xiàn)[2]中有詳細(xì)論述，而應(yīng)用于10～95 kHz的窄帶電力線噪聲的仿真模型還沒有明確的推論.早期的研究顯示電力環(huán)境中的噪聲不是加性高斯白噪聲(AWGN)[3].為了仿真噪聲，許多文獻(xiàn)提出了不同的噪聲的統(tǒng)計模型，脈沖噪聲的統(tǒng)計屬性可以在文獻(xiàn)[4]中發(fā)現(xiàn)；背景噪聲的功率譜密度在文獻(xiàn)[5]中建立；一種忽略脈沖噪聲隨機(jī)性的確定性窄帶噪聲數(shù)學(xué)模型在文獻(xiàn)[6]中給出.然而，目前沒有一種電力噪聲模型，考慮了脈沖噪聲在實際電力環(huán)境中包絡(luò)和時間的分布.

由于電力噪聲分布的多樣性和隨機(jī)性，用一種確定的數(shù)學(xué)模型很難體現(xiàn)其物理屬性.本文通過構(gòu)建真實電力線噪聲的測量環(huán)境，記錄并分析實測噪聲，對其中的背景噪聲和脈沖噪聲進(jìn)行了建模和仿真.前者的時域模型由高斯白噪聲通過滾降系數(shù)為‘1’的滾降濾波器而得到，其功率近似服從正態(tài)分布；后者的時域模型由服從確定統(tǒng)計規(guī)律的特性參數(shù)所描述，特性參數(shù)根據(jù)實際測量的數(shù)據(jù)統(tǒng)計得到，其時域的仿真波形由MCMC分析得到.

1 噪聲模型

根據(jù)背景噪聲的平穩(wěn)分布性和脈沖噪聲的隨機(jī)分布性，利用實際測量數(shù)據(jù)分別對兩種噪聲進(jìn)行統(tǒng)計建模，再將兩種噪聲疊加[7]，得到實測的電力噪聲模型.

1．1 噪聲測量

文中所述噪聲的測量均按圖1所示系統(tǒng)實現(xiàn).電力信號首先通過容性耦合器，將50 Hz的工頻電壓諧波噪聲濾除，然后通過10～500 kHz的帶通濾波器，得到窄帶電力噪聲，最后由大容量數(shù)據(jù)存儲的數(shù)字采集器記錄保存.濾波器采用3階巴特沃斯帶通濾波器[8]，線性中心頻率為255 kHz.數(shù)字采集器的型號為USB2085，實現(xiàn)A/D轉(zhuǎn)換和數(shù)據(jù)采集的功能，設(shè)置其采樣頻率為400 kHz，采集時長為10 min/次.

圖1 測量系統(tǒng)

現(xiàn)選湖南大學(xué)13舍實驗樓作為測試點，對七樓配電箱A相進(jìn)行分時段的連續(xù)測量記錄，根據(jù)用電負(fù)荷和噪聲干擾的不同，分成3個時段進(jìn)行測量:輕量噪聲時段，00:00-06:00;中量噪聲時段，12:00-13:00和重量噪聲時段，14:00-17:00.測量總時長為6 361 min，約106 h.

1．2 背景噪聲模型

電力背景噪聲屬于平穩(wěn)分布的彩色噪聲，其功率主要集中于低頻段.圖2為去除窄帶及脈沖噪聲后背景噪聲的功率譜密度，3個時段的噪聲在頻率最低處，功率最大，集中于-10 dB附近，隨著頻率的增大，功率減小，所以具有低通特性.因此背景噪聲的時域模型ηc(t)，可以由加性高斯白噪聲(AWGN)ξ(t)，通過滾降系數(shù)為‘1’的升余弦滾降濾波器而得到：

(1)

式中ξ(t)的功率譜密度為n0，通過測量數(shù)據(jù)的統(tǒng)計和中心極限定律分析[9]，n0近似服從高斯分布：n0～N(-10,2).升余弦滾降濾波器的參數(shù)f0，由背景噪聲功率譜下降的速度決定.最低頻點和最高頻點功率的比值Pc，是濾波器在95kHz的頻域值：

(2)

頻率/(104 Hz)

1．3 脈沖噪聲模型

脈沖噪聲分為同步的周期性和異步的非周期性脈沖噪聲.對于前者，因為具有確定性，所以建模相對簡單；但是對于后者，因為時間和包絡(luò)參數(shù)分布的隨機(jī)性，所以必須用一個隨機(jī)模型來描述，同時其特性參數(shù)服從確定的分布律.

1．3．1 脈沖噪聲模型

圖3為實測脈沖噪聲的時域波形，顯然，每個脈沖可由3個特性參數(shù)描述：包絡(luò)av，寬度tw和間隔td.其脈沖函數(shù)表述如下[5]：

時間/ms

(3)

式中K是脈沖的總數(shù);ta是脈沖噪聲的到達(dá)時間，由脈沖的寬度和間隔決定.根據(jù)圖3可知，脈沖噪聲具有指數(shù)衰減的正弦波振蕩特性，所以時域模型可由下式表示：

imp(t)=

(4)

在式(4)中，衰減因子d由脈沖噪聲的寬度tw決定，表示脈沖下降的速度；振蕩頻率fosc決定了在一個脈沖寬度內(nèi)，正弦波振蕩的個數(shù).令fosc=fs/2,

(5)

基于式(3)～(5)，特性參數(shù)tw，td，av和脈沖的總數(shù)K完全確定了脈沖噪聲的時域波形，這些參數(shù)由時域測量數(shù)據(jù)的統(tǒng)計分析得到.

1.3.2 參數(shù)確定

這一節(jié)主要確定上節(jié)中所推得脈沖噪聲的個數(shù)和特性參數(shù)的分布規(guī)律.

為確定脈沖的個數(shù)，取觀察時長為1 s，定義在此時間內(nèi)脈沖的總數(shù)為沖激率rimp，脈沖的總時長為干擾率dr，得到測量數(shù)據(jù)的統(tǒng)計值如表1所示.

表1 測量數(shù)據(jù)的沖激率和干擾率統(tǒng)計

rimp和dr可以用下式表達(dá)：

(6)

式中NA和Np分別是異步脈沖和周期脈沖的個數(shù).結(jié)合式(6)，表1可以通過脈沖的來源和數(shù)量來解釋.在重量噪聲時段，因為是工作時段，供電電源以同步于工頻電壓主頻的速度持續(xù)動作，所以大量短時寬的周期脈沖占主導(dǎo)，即使脈沖的平均個數(shù)達(dá)到161個，但是所占時間仍然不足總時長的2%；在輕量噪聲時段，實驗樓內(nèi)沒有大量的用電設(shè)備，這時會有開關(guān)的瞬態(tài)過程，所以大部分是異步脈沖，周期脈沖可以忽略.因此在由“輕量噪聲組”進(jìn)入“重量噪聲組”，周期性脈沖迅速增加.因為測量是在同一點位置進(jìn)行的，所以3組時段異步脈沖的個數(shù)保持不變.基于此NA，NP和周期脈沖的tw_p可以推導(dǎo)如下：

(7)

式中rimp_wa和dr_wa是輕量噪聲組的統(tǒng)計平均值，在表1中可以得到.

異步脈沖噪聲的特性參數(shù)tw，td和av的測量統(tǒng)計見圖4，其變化趨勢近似服從指數(shù)分布，所以用分段馬氏鏈[10]來描述，過概率(AdvancedProbabilitiesDensity,APD)如下：

(8)

式中pNn和pnn是馬爾克夫鏈的邊沿和對角轉(zhuǎn)移概率，x是時間離散化的值.令pr為邊沿和對角概率的比值，對角概率為pd，則分段馬氏鏈的概率密度函數(shù)可以由式(8)推得：

(9)

從式(9)可見，Pb_t和Pdf_t由加權(quán)指數(shù)函數(shù)構(gòu)成，所以其系數(shù)pr和pd，可以通過最小二乘曲線擬合技術(shù)，從tw，td和av的測量統(tǒng)計值得到，如圖4所示.

圖4描述了輕量噪聲組的特性參數(shù)概率分布，圈劃線為測量統(tǒng)計，虛線是根據(jù)式(8)得到的,而直方圖是對擬合的概率模型的仿真.由圖4可見，脈沖噪聲的統(tǒng)計模型，完全由實際環(huán)境的測量數(shù)據(jù)得到.而模型的仿真采樣基于MCMC算法，因為所研究的窄帶頻段限制在10～95kHz，所以確定采樣頻率fs=0.4MHz，這正是窄帶OFDM的采樣頻率.選取仿真時長為1s，則每個周期有4×105個樣點.

脈沖幅度/V

脈沖寬度/ms

脈沖間隔/ms

2 噪聲仿真

電力噪聲的仿真主要為背景噪聲和脈沖噪聲的仿真，再將兩部分疊加，得：

η(t)=ηc(t)+ηimp(t)

其中背景噪聲仿真主要是設(shè)計升余弦滾降濾波器，其截止頻率由式(2)決定，功率譜密度由服從均值為-10，方差為2的正態(tài)分布的采樣得到.

脈沖噪聲的模型，因為參數(shù)是服從確定分布律的隨機(jī)量，所以用MCMC能夠得到快速收斂的仿真值.從圖4可見，av和tw的測量統(tǒng)計具有快衰落的特點，在20個采樣點后PDF(概率密度分布)已經(jīng)低于10-4，所以用經(jīng)典MCMC算法：Metropolis-Hastings(MH) 來仿真這兩個量.畫出仿真樣點直方圖，可以看出他們完全按照參數(shù)的概率分布模型抽取.

對于脈沖間隔td，概率密度分布于0～16 000ms，變化緩慢，包括200 000個樣點，用經(jīng)典MCMC算法很難達(dá)到收斂，所以采Multiple-Try-Metropolis(MTM) 算法[11]，與經(jīng)典MH算法比較，在不降低接受率的條件下，MTM具有更大步長的跳躍.這種算法首先產(chǎn)生幾個相關(guān)樣點，然后從中選擇一個最優(yōu)點.在這種算法中，目標(biāo)分布和提議分布分別是概率密度函數(shù)Pdf_t(x)和正態(tài)分布函數(shù)N(x).為得到新的采樣，給定初始值為x0.一般，在MCMC算法的權(quán)重函數(shù)中給出更多的統(tǒng)計信息，能夠改善仿真的性能.所以權(quán)重函數(shù)構(gòu)造如下：

(10)

接受函數(shù)和權(quán)重函數(shù)之間的關(guān)系是：

(11)

則MTM算法的步驟如下：

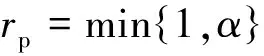
3 模型評價

為了驗證提議的模型，將實際電力噪聲的測量值與提議模型的仿真值進(jìn)行比較.在重量組選擇5組具有不同(rimp,dr)的測量數(shù)據(jù)，仿真時長設(shè)置為20s.根據(jù)每組(rimp,dr)，仿真100組基于提議模型的隨機(jī)噪聲，統(tǒng)計仿真組的(rimp,dr)和均方功率[12]，并與測量值比較.

圖5為相同(rimp,dr)條件下，測量值和仿真值的時域波形和功率譜密度，從圖中可見，時頻域波形比較接近.基于測量數(shù)據(jù)及仿真數(shù)據(jù)的干擾率和均

圖5 測量值和仿真值的時頻域波形比較

方功率的比較如圖6所示.橫坐標(biāo)是沖激率，縱坐標(biāo)是干擾率和均方功率，仿真數(shù)據(jù)的均方功率曲線和干擾率曲線很好地擬合了測量數(shù)據(jù)的相應(yīng)曲線.

圖6 測量值和仿真值的沖激率和均方功率比較

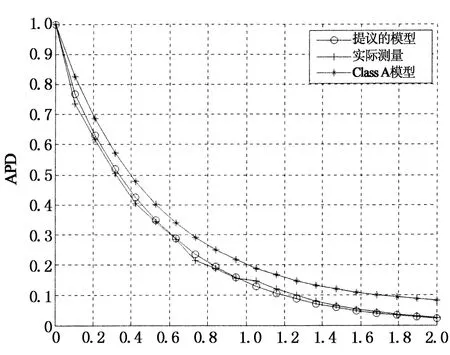
為使評價更加完善，現(xiàn)選取應(yīng)用比較多的ClassA噪聲模型，使其與提議模型和實際測量的APD相比較.ClassA模型的APD定義如下：

(12)

圖7為Class A模型、提議模型和實際測量數(shù)據(jù)的APD比較，測量噪聲選取輕量噪聲時段數(shù)據(jù).因為這一時段的噪聲主要是異步非周期性脈沖噪聲和背景噪聲，所以其APD曲線比較平滑，對實際測量的APD應(yīng)用EM 算法[13]，確定Class A模型的參數(shù)：A=0.5,G=0.1，利用式(8)得提議模型的參數(shù).從圖7可見，提議模型的APD與實測數(shù)據(jù)更為接近.

從以上對不同模型的比較評價，提議模型均能更好地逼近實測數(shù)據(jù)，所以在研究窄帶電力載波通信技術(shù)時，可以用提議模型仿真實際的電力線噪聲.

幅度/V

4 結(jié) 論

電力線環(huán)境作為通信信道時具有非高斯分布的噪聲特性.因此應(yīng)用高斯噪聲作為信道干擾，進(jìn)而設(shè)計和評價電力載波通信算法，其實質(zhì)并不適應(yīng)于電力線環(huán)境.為此本文根據(jù)實際測量電力噪聲的統(tǒng)計分析，提出基于隨機(jī)分布的特性參數(shù)所描述的隨機(jī)模型.其中背景噪聲模型由AWGN通過升余弦滾降濾波器得到；脈沖噪聲模型由脈沖包絡(luò)、寬度和間隔所限定的隨機(jī)模型得到.通過MCMC算法仿真，得到模型的實現(xiàn)，最后通過與實測數(shù)據(jù)的比較證明了所提議的模型可以用來仿真實際的電力線噪聲.

[1] JAVIER M, SADOT A, RODRIGUEZ-MORCILLO C. Performance evaluation of two narrowband PLC systems: PRIME and G3 [J].Comput Stand Inter, 2013, 36(1): 198-208.

[2] ZIMMERMANN M, DOSTERT K. A multipath model for the power line channel [J]. IEEE Trans Commun, 2002, 50(4):555-559.

[3] GOTZ M, RAPP M,DOSTERT K. Power line channel characteristics and their effect on communication system design [J]. IEEE Communications Magazine, 2004, 42(4):78-86.

[4] ZIMMERMANN M, DOSTERT K. Analysis and modeling of impulsive noise in broad-band powerline communications [J]. IEEE Trans Electromagn Compat, 2002, 44(1): 249-258.

[5] HOOIJEN O G. A channel model for the residential power circuit used as a digital communications medium [J]. IEEE Trans Power Del, 2004, 19(3): 1057-1064.

[6] KATAYAMA M, YAMAZATO T, OKADA H. A mathematical model of noise in narrowband power line communication systems [J]. IEEE J Sel Area Comm, 2006, 24(7): 1267-1276.

[7] ANDREADOU N, PAVLIDOU F N. Modeling the noise on the OFDM power-line communication system [J]. IEEE Trans Power Del, 2010, 25(1): 150-157.

[8] YAO S N,COLLINS T,JAN P.Hybrid method for designing digital butter worth filters[J]. Comput Electr Eng, 2012, 38(4): 811-818.

[9] MORRIS H DeGroot, MARK J Schervish. Probability and statistics[M]. 3rd ed. New York:Addison-Wesley, 2002: 219-237.

[10] THOMAS Kaijser. On Markov chains induced by partitioned transition probability matrices [J]. ActaMathematica Sinica, 2011, 27(3): 221-227.

[11] MARTINO L, DEL Olmo V P, READ J. Amulti-point metropolis scheme with generic weight functions [J]. Statistics and Probability Letters, 2012, 82(7): 121-134.

[12] 于善奇. 統(tǒng)計方法引論 [M]. 第2 版.北京：北京工業(yè)大學(xué)出版社，2014:251-267.

YU Shan-qi. Introduction to statistical methods [M].2nd ed. Beijing: Press of Beijing University of Technology, 2014:251-267.(In Chinese)

[13] CHEN Shu-chuan, LINDSAY Bruce. Improving mixture tree construction using better EM algorithms[J]. Computational Statistics & Data Analysis, 2014, 74(5): 17-25.

Modeling Narrow-band Power Line Noise Based on Distribution of Field Noise Measurement

GU Zhi-ru1, LIU Hong-li1?, TAN Zhou-wen1, LIU Shu-gang2

(1．College of Electrical and Information Engineering, Hunan Univ, Changsha，Hunan 410082，China;2．Physics and Electronic Science, Hunan Univ of Science and Technology, Xiangtan,Hunan 519000,China)

Based on the distribution of measurement, a Non-Gaussian model of narrow-band power line noise including background noise and impulsive noise was derived, The background noise, which follows Gaussian distributions, was modeled with a raised cosine roll-off filter, while the impulsive noise was modeled with impulse width, interarrival times and envelope parameters, whose distribution follows partitioned Markov chain. Then, the model was evaluated with some field measurement data and the Markov Chain Monte Carlo (MCMC) analysis. The evaluation results show that the proposed model can approximate the noise in real environment.

power line communication; smart grid; orthogonal frequency division multiplexing; partitioned Markov chain; Markov Chain Monte Carlo

1674-2974(2015)02-0081-06

2014-07-26

國家自然科學(xué)基金資助項目(61172089),National Natural Science Foundation of China(61172089)；高等學(xué)校博士學(xué)科專項科研基金資助項目(20120161120012)；湖南省科技計劃資助項目(2014WK3001)

谷志茹(1979-)，女，河南開封人，湖南大學(xué)博士研究生?通訊聯(lián)系人，E-mail:hongliliu@vip.sina.com

TPN14

A