RC框架結構Pushover方法的保證率和適用性研究

張望喜，張穎波，張 勇，易偉建，肖 巖

(湖南大學 土木工程學院, 湖南 長沙 410082)

RC框架結構Pushover方法的保證率和適用性研究

張望喜?，張穎波，張 勇，易偉建，肖 巖

(湖南大學 土木工程學院, 湖南 長沙 410082)

以7層鋼筋混凝土平面框架結構為例，通過統計分析不同地震烈度、不同場地條件、不同地震分組的平面框架在不同抗震設防水準條件下的Pushover分析性能點的概率分布，探討Pushover分析方法的保證率和適用性.研究表明，Pushover分析方法是一種靜力彈塑性分析方法，不適用于結構彈性抗震性能評估.

混凝土框架結構；Pushover分析方法；概率分析

基于性能的抗震設計理論是未來結構抗震設計的發展方向，正如FEMA[1]研究報告指出：基于性能的抗震設計框架應該以可靠度為基礎.歐進萍等[2]結合我國抗震規范和地震作用統計參數，提出了概率Pushover分析方法，并且考慮結構體系可靠度的特點，提出了基于概率Pushover分析的結構體系抗震可靠度評估方法.易偉建和蔣蝶[3]在已有研究基礎上，結合我國01版抗震規范和地震作用統計參數提出了Pushover分析方法中抗力曲線保證率的計算方法.概率Pushover分析方法受到了國內外學者的廣泛關注與研究.

但是基于概率的Pushover分析方法理論還不夠成熟，自歐進萍[2]等提出概率Pushover分析方法后，在國內外刊物上能找到的關于這個問題的文獻較少；關于這個問題的研究大多是針對具體結構的研究，具有普遍性和一般結論性的研究成果較少；有一些理論成果僅僅停留在理論層面[4-5]，因此該方法很難應用于實際工程.

在這種情況下，對現行的確定性Pushover分析方法的保證率和適用范圍進行研究是很有必要的．頂點位移是Pushover分析結果的關鍵指標，本文通過探討Pushover分析頂點位移的概率分布來研究確定性Pushover分析方法的保證率和適用性.

1 實際需求譜Pushover分析方法

采用實際需求譜Pushover分析方法求解某條地震波對應的精確性能點方法詳見文獻[6]．本文采用實際需求譜Pushover分析方法研究確定性Pushover分析方法頂點位移的保證率時，不需要求出每條地震波對應的精確頂點位移，只需判斷這些性能點譜位移與確定性Pushover分析性能點譜位移的大小關系，因為2種Pushover分析方法的結構模型相同，2種分析方法性能點在相同能力曲線上，基底剪力和譜位移呈線性關系.

實際需求譜Pushover分析方法性能點譜位移與確定性Pushover分析方法性能點譜位移有3種關系：

1)實際彈性需求譜與能力曲線交點譜位移小于確定性Pushover分析性能點譜位移.此時確定性Pushover分析相對實際需求譜Pushover分析偏于保守，見圖1(a).

2)實際彈性需求譜對應的性能點譜位移大于確定性Pushover分析性能點譜位移，按確定性Pushover分析性能點延性系數折減后的實際彈塑需求譜與能力曲線交點譜位移小于確定性Pushover分析性能點譜位移.此時性能點在能力曲線上延性系數偏小，在需求曲線上偏大，經過多次迭代后實際需求譜Pushover分析精確性能點會落在確定性Pushover分析性能點和該彈塑性需求譜對應的性能點之間.這種情況下確定性Pushover分析相對實際需求譜Pushover分析偏于保守，見圖1(b).

3)實際彈性需求譜對應的性能點譜位移大于確定性Pushover分析性能點譜位移，按確定性Pushover分析性能點對應的延性系數折減后的彈塑性反應譜與能力曲線交點譜位移大于確定性Pushover分析性能點譜位移.此時性能點在能力曲線上延性系數偏大，在需求曲線上偏小，經過多次迭代后實際需求譜Pushover分析精確性能點會落在確定性Pushover分析性能點和該彈塑性需求譜對應的性能點之間.該情況下確定性Pushover分析相對實際需求譜Pushover分析偏于不安全，見圖1(c).

本文探討確定性Pushover分析方法的保證率就是統計前面2種情況地震波數量與所選用總地震波數量的比值.對于每種情況本文從美國太平洋地震工程研究中心強震數據庫中隨機選取50條地震波進行統計分析.

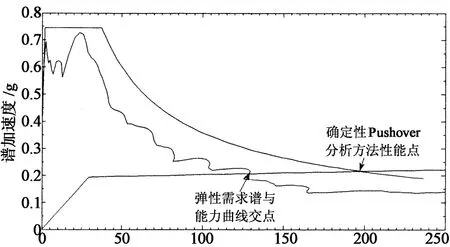
譜位移/mm(a)

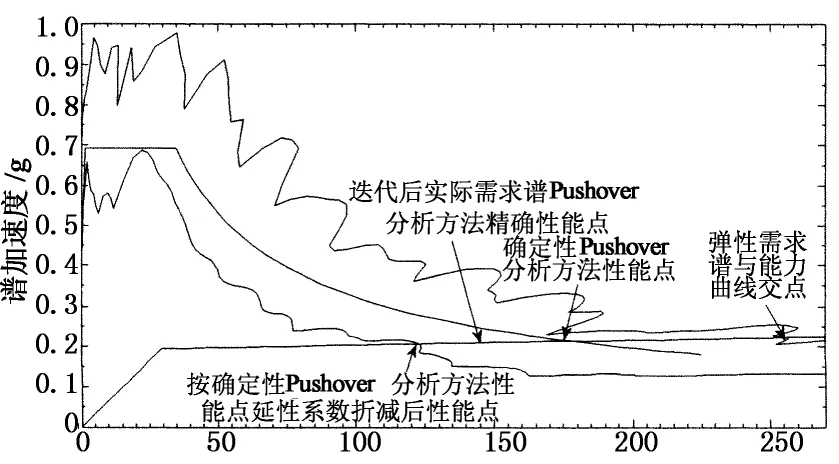
譜位移/mm(b)

譜位移/mm(c)

2 平面框架分析模型

本文研究設防烈度為6度～9度的各種場地條件(見圖2)下的平面框架在不同設防水準的Pushover分析頂點位移的概率分布.我國抗震規范[7]規定9度區的框架結構不得超過24 m，文獻[5]研究表明在此高度條件下規則平面框架性能點對需求曲線的敏感性遠遠強于能力曲線，探討Pushover分析方法頂點位移的概率分布時，可以忽略能力曲線的不確定性，僅考慮需求曲線的不確定性.本文Pushover分析滯回模型選用三線性模型，側向荷載加載模式采用倒三角形加載模式.

圖2 平面框架所在的場地條件

本文探討的框架結構為7層3跨的平面，混凝土強度為C30，梁、柱縱筋采用HRB335框架，跨度為6 m，底層層高為3.9 m，其余樓層層高3.3 m，建筑總高度23.7 m.梁、柱級鋼筋，箍筋采用HPB300級鋼筋，平面框架模型如圖3所示.7度(0.1g)Ⅱ類二組場地條件平面框架截面信息見表1，本文所采用的本構關系參考混凝土結構設計規范[8]和IDARC用戶指南[9]，如圖4和圖5所示.

圖3 7層平面框架結構布置圖

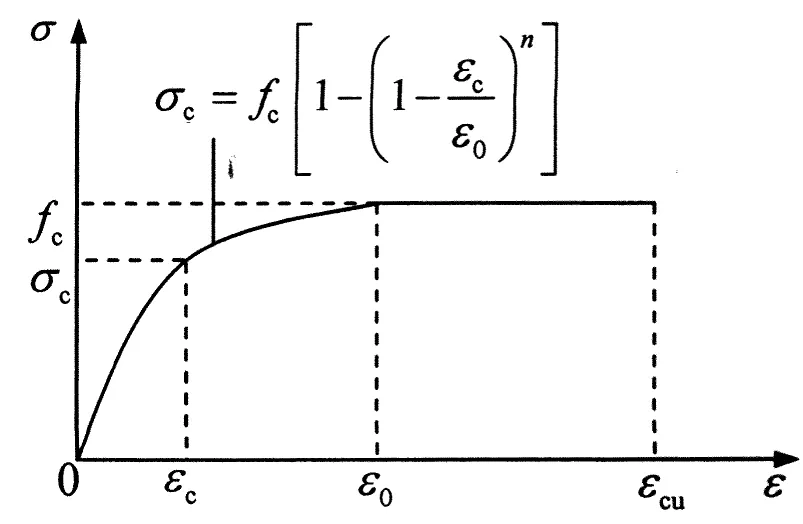
圖4 混凝土本構關系

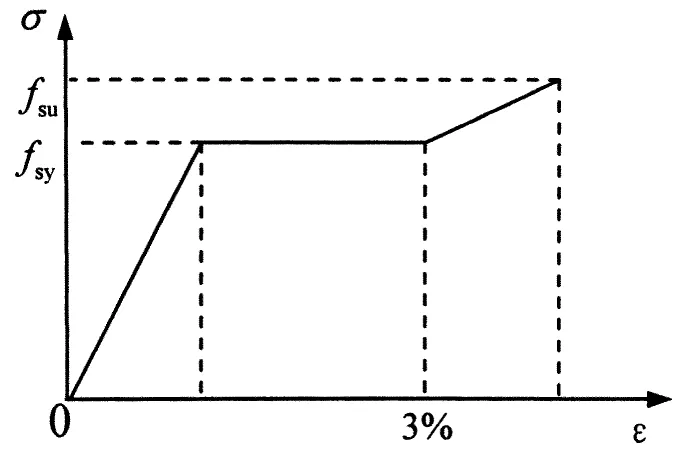
圖5 鋼筋本構關系

表1 7度(0.1 g)Ⅱ類二組場地條件平面框架截面信息

建立好6度～9度各種場地條件下的7層平面框架后，對其進行確定性Pushover分析，結構抗力不確定性因素均取均值.將各種條件下平面框架的基底剪力-頂點位移曲線轉化成能力曲線見圖6.

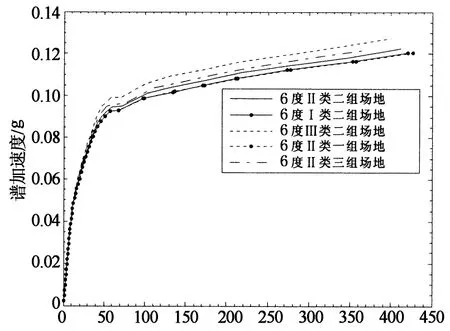
譜位移/mm(a)6度設防能力曲線

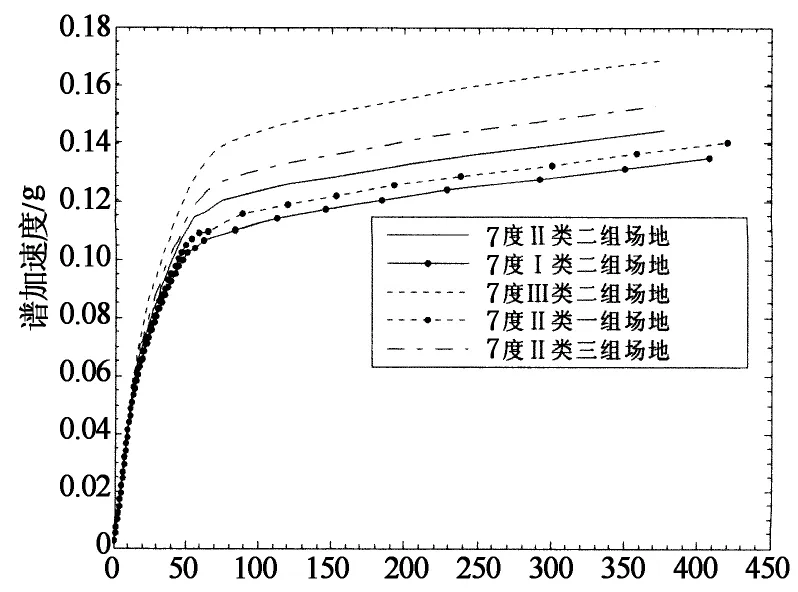
譜位移/mm (b)7度設防能力曲線

譜位移/mm (c)8度設防能力曲線

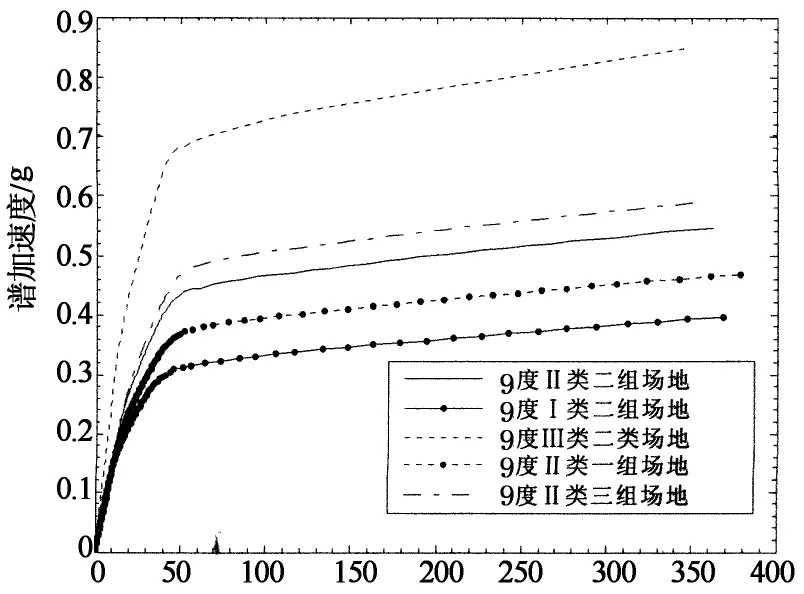
譜位移/mm (d)9度設防能力曲線

從圖6可以看出，隨著地震設防烈度的增加，相同場地條件和地震分組的平面框架Pushover分析能力曲線譜加速度逐漸增大，不同條件下的能力曲線越來越離散.可見地震烈度越高，場地條件和地震分組對Pushover分析能力曲線的影響越明顯.

采用自編MatLab程序求解各種條件下的平面框架在多遇地震、設防地震和罕遇地震條件下的性能點和頂點位移， 8度Ⅱ類二組平面框架在設防地震條件的性能點求解圖如圖7所示.

譜位移/mm

多遇地震、設防地震和罕遇地震的超越概率[6]分別為63.5%,10%和2%，則其保證率分別為36.5%,90%和98%.通過實際需求譜Pushover分析方法統計出各種場地條件的平面框架在確定地震烈度條件下各個設防水準對應的確定性Pushover分析方法的保證率后，僅考慮地震烈度和場地條件的不確定性，且忽略其相關性，采用條件概率方法求解Pushover分析方法的保證率.如8度Ⅱ類二組場地的平面框架，在確定地震烈度條件下罕遇地震對應的確定性Pushover分析方法保證率為100%.綜合考慮地震烈度和場地條件的不確定性，8度Ⅱ類二組平面框架Pushover分析頂點位移在罕遇地震下的保證率為98%×100%=98%.各個地震烈度、不同場地條件不同設防水準的平面框架Pushover分析頂點位移的保證率見表2～表5.

表2 6度平面框架在各個設防水準條件下頂點位移保證率

表3 7度平面框架在各個設防水準條件下頂點位移保證率

表4 8度平面框架在各個設防水準條件下頂點位移保證率

表5 9度平面框架在各個設防水準條件下頂點位移保證率

3 結 論

通過上述分析可以得到以下結論：

1)場地類別從Ⅰ類到Ⅲ類，確定性Pushover分析方法保證率在罕遇地震條件下的變化規律是先增大再降低；在設防地震和多遇地震條件下，保證率逐漸增大.

2)地震分組從一組到三組，確定性Pushover分析方法保證率在各個設防水準條件下的總體變化規律是先降低然后升高.

3)在罕遇地震和設防地震條件下，隨著設防烈度的增加，確定性Pushover分析方法保證率總的變化趨勢是增加的，在多遇地震條件下，保證率均較低且沒有明顯規律，主要是因為我國抗震規范采用的地震設防水準規定多遇地震50年的超越概率為63.2%.

4)隨著設防水準從多遇地震到設防地震再到罕遇地震，確定性Pushover分析方法的保證率逐漸升高.

5)若在地震作用下結構變形進入彈塑性狀態：即在各設防烈度的罕遇地震條件下和8度、9度的設防地震條件下，Pushover分析結果保證率很高，此時該方法是一種可靠的抗震性能評估方法；若在地震作用下結構變形始終處于彈性狀態：即在各設防烈度的多遇地震條件下和6度、7度的設防地震條件下， Pushover分析結果保證率較低，分析結果偏于不安全.由此可知Pushover分析方法是一種靜力彈塑性分析方法，不適用于靜力彈性分析.

[1] FEMA273/274 NEHRP commentary on the guidelines for rehabilitation of building[R]. Washington, DC:Federal Emergency Management Agency, 1996.

[2] 歐進萍,侯綱領,吳斌,等.概率Pushover分析方法及其在結構體系抗震可靠度評估中的應用[J].建筑結構學報,2001,22(6):81-86.

OU Jin-ping, HOU Gang-ling, WU Bin,etal. Random pushover analysis method and its application in earthquake-resistant reliability evaluation of structural systems[J]. Journal of Building Structures, 2001, 22(6): 81-86.(In Chinese)

[3] 易偉建,蔣蝶.Pushover分析中抗力曲線的概率研究[J].地震工程與工程振動,2009,29(1):78-82.

YI Wei-jian, JIANG Die. Probabilistic research on capacity curve in pushover analysis[J]. Earthquake Engineering and Engineering Vibration,2009,29(1): 78-82. (In Chinese)

[4] 朱俊鋒,王東煒,霍達.在大震下RC框架結構基于Pushover方法的失效相關性分析[J]. 地震工程與工程振動,2005,25(4):85-90.

ZHU Jun-feng, WANG Dong-wei, HUO Da. An analysis of failure dependencies of RC frame structures based on Pushover method under strong earthquakes[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(4): 85-90.(In Chinese)

[5] 侯爽,歐進萍. 鋼筋混凝土框架結構體系抗震可靠度及其抗力衰減影響分析[J]. 地震工程與工程振動,2006, 26(5): 114-119.

HOU Shuang, OU Jin-ping. Earthquake-resistant system reliability analysis of reinforced concrete frame structure and the influence of resistance attenuation[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5): 114-119. (In Chinese)

[6] 張望喜, 張勇, 易偉建, 等. RC框架結構pushover方法頂點位移的敏感性分析[J].湖南大學學報:自然科學版,2014,41(2):14-18.

ZHANG Wang-xi, ZHANG Yong, YI Wei-jian,etal. Sensitivity analysis of the top displacement of the pushover analysis method of reinforced concrete frame structure[J]. Journal of Hunan University: Natural Sciences, 2014,41(2):14-18.(In Chinese)

[7] GB 50011—2010 建筑抗震設計規范[S].北京:中國建筑工業出版社,2010:48-73.

GB 50011—2010 Code for seismic design of buildings[S]. Beijing: China Architecture & Building Press, 2010:48-73.(In Chinese)

[8] GB 50010—2010 混凝土結構設計規范[S].北京:中國建筑工業出版社,2010:34-35.

GB 50010—2010 Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2010: 34-35.(In Chinese)

[9] REINHORN A M, ROH H, SIVASELVAN M,etal. IDARC 2D Version 7.0 USER’S GUIDE [EB/OL]// [2010-01-01]http://civil.eng.buffalo.edu/idarc2d50/ Jan. 2010．

Research on the Guarantee Rate and Suitability of Pushover Analysis Method for Reinforced Concrete Frame Structure

ZHANG Wang-xi?, ZHANG Ying-bo , ZHANG Yong , YI Wei-jian , XIAO Yan

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082,China)

Based on a 7-story reinforced concrete plane frame structure, the guarantee rate and suitability of Pushover analysis method were discussed by statistically analyzing the probability distribution of the performance point of the Pushover analysis method of plane frames with different seismic intensities, site conditions and design earthquake groups in various seismic fortification levels. The results show that Pushover analysis method is a static elastic-plastic analysis method, which is not suitable for evaluating the structural elastic seismic behaviour.

reinforced concrete frame structure; Pushover analysis method; probability analysis

1674-2974(2015)03-0009-05

2014-04-09

國家自然科學基金資助項目(51078133,51208190)，National Natural Science Foundation of China(51078133,51208190)

張望喜(1971-)，男，湖北黃岡人，湖南大學副教授，博士

?通訊聯系人，E-mail:wxizhang2000@163.com

TU318.1

A