表面粗糙度對雙曲冷卻塔風壓分布的影響*

鄒云峰，何旭輝，王漢封，譚立新，牛華偉

(1．中南大學 土木工程學院，湖南 長沙 410075；2．高速鐵路建造技術國家工程實驗室，湖南 長沙 410075；3．中國建筑第五工程局有限公司，湖南 長沙 410004；4．湖南大學 風工程試驗研究中心，湖南 長沙 410082)

表面粗糙度對雙曲冷卻塔風壓分布的影響*

鄒云峰1,2,3，何旭輝1,2?，王漢封1,2，譚立新3，牛華偉4

(1．中南大學 土木工程學院，湖南 長沙 410075；2．高速鐵路建造技術國家工程實驗室，湖南 長沙 410075；3．中國建筑第五工程局有限公司，湖南 長沙 410004；4．湖南大學 風工程試驗研究中心，湖南 長沙 410082)

對不同粗糙條參數組合下冷卻塔風壓分布進行測試，分析粗糙度對平均風壓和脈動風壓的影響.研究結果表明：粗糙條寬度b對風壓分布影響較小，而粗糙條高度k和數量n影響較大；粗糙度系數k/s能較準確描述粗糙度大小，當k/s一致時，不同粗糙條數量n與高度k組合下的平均風壓基本一致，但高度大的脈動風壓小；粗糙度對正壓分布和背壓大小影響較小，而最小負壓系數幅值、脈動風壓系數峰值隨粗糙度的增大而減小，背壓穩定區寬度則略有擴大；盡管通過增大模型表面粗糙度能有效地在較低雷諾數條件下實現高雷諾數下的平均風壓分布，但脈動風壓模擬的準確性需要通過大型冷卻塔風壓實測進行驗證.

冷卻塔；表面粗糙度；風壓分布；風洞試驗

冷卻塔屬類圓截面結構，風壓分布受表面粗糙度和雷諾數影響顯著.風洞試驗由于采用縮尺模型導致試驗雷諾數比實際的小2～3個數量級，又由于風洞試驗中風速的限制，很難通過增加試驗風速來提高雷諾數，因此一般通過增大模型表面粗糙度對類圓截面結構的雷諾數效應進行補償[1-2].此外，隨著冷卻塔高度的增加，國外通常在風筒外表面設置子午向肋條來增大表面粗糙度以減小最小風壓系數幅值[3-4].

目前，已有一些文獻研究了表面粗糙度對冷卻塔風荷載的影響.Armitt發現在一定粗糙度范圍內，可以通過增加模型表面粗糙度模擬較高雷諾數下的光塔平均風壓[5]；Farell等研究表明最小負壓系數隨粗糙度的增大而減小[6]；Niemann分析了粗糙度對最小負壓、背壓等冷卻塔風壓曲線特征值的影響，并給出不同粗糙度下的擬合曲線[7]；孫天風等發現最小壓力系數幅值隨著表面粗糙度的增大而減小，粗糙度大小與粗糙條厚度和數量有關[8]；劉天成等對刻線和粘貼絲線、粗糙紙帶等多種增大表面粗糙度手段對雷諾數效應補償效果對比，發現粘貼粗糙紙帶較為有效且便于操作[9]；沈國輝等通過兩種粗糙條數量和五種粗糙條厚度對比分析發現結構的整體受力隨粗糙條數量和厚度的增加而增大[10]；董國朝等的數值模擬結果表明冷卻塔表面混凝土粗糙度對風壓分布的影響不容忽視[11].以上研究主要定性分析粗糙度對冷卻塔平均風荷載的影響，幾乎沒有涉及脈動風荷載；沒有總結出合理的粗糙度系數，未能定量分析粗糙度對風壓分布的影響大小.如何調整粗糙度以保證在風洞試驗中模型表面繞流特性與原型一致或接近以確保風洞試驗結果可靠，怎樣考慮子午向肋條(寬度、高度、間距等)對風壓分布的影響以確保原型冷卻塔表面的風壓分布與設計曲線(加肋曲線)相符，等等.這些問題的解決需要對表面粗糙度影響風壓分布(平均風壓和脈動風壓)的規律進行系統地深入分析.

本文進行粗糙條參數如數量、厚度、寬度等多種組合工況的冷卻塔剛性模型測壓試驗，對脈動風壓進行反演修正以確保其測試結果的可靠性，較系統的分析粗糙條參數對冷卻塔風壓分布的影響，定義更為合理的粗糙度系數，總結粗糙度系數與風壓分布曲線之間的關系，并與實塔測試結果驗證.研究成果為全面認識表面粗糙度對冷卻塔風壓分布的影響提供參考.

1 風洞試驗概況

1.1 試驗模型

某核電站擬建冷卻塔塔頂標高200.20 m，喉部標高156.70 m，進風口標高12.59 m，塔頂直徑96.60 m，喉部直徑94.60 m，底部直徑153.00 m，風筒采用分段等厚，最小厚度在喉部斷面為0.25 m，最大厚度在下環梁位置為1.4 m，由均勻分布的52對人字柱支撐.試驗模型幾何縮尺比為1/400，采用圓柱型鋁錠通過數控機床精加工而成，精度可達±0.01 mm，嚴格保證外形與實際結構保持幾何相似，模型底部由縮尺的人字柱支撐.模型壁厚6 mm，保證模型具有足夠的強度和剛度，在試驗風速下不發生變形及不出現明顯的振動.在模型表面共布置20層測點，每層沿環向等間距布置36個測點，共計720個測點，測點布置如圖1所示.試驗在湖南大學HD-2風洞的高速試驗段進行，試驗段長17 m，寬3 m，高2.5 m.為使試驗結果更具普遍性，本次試驗在均勻流場中進行.

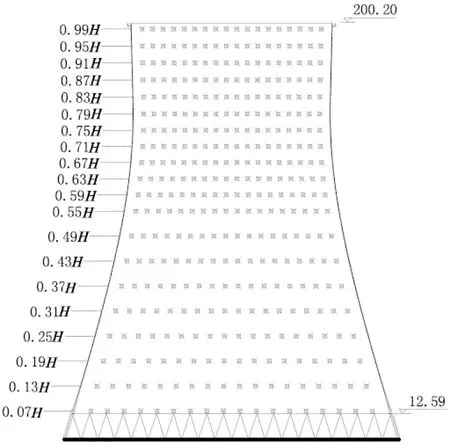
圖1 測壓點布置

1.2 試驗工況

參考常用方法，通過在模型表面沿環向等間距粘貼子午向通長的粗糙紙帶增大表面粗糙度，粗糙度大小改變通過調整紙帶寬度、厚度、數量實現，其中，紙帶寬度考慮5,8,10,15 mm 4種，厚度在0.0(光塔)～0.8 mm范圍內以0.1 mm為增量逐一變化，數量考慮36,72條2種，試驗風速在6～20 m/s內以2 m/s為增量逐一變化，對應的雷諾數范圍為0.99×105～3.3×105，總共約進行了200個吹風工況.詳細的工況安排見表1，部分試驗照片如圖2所示.

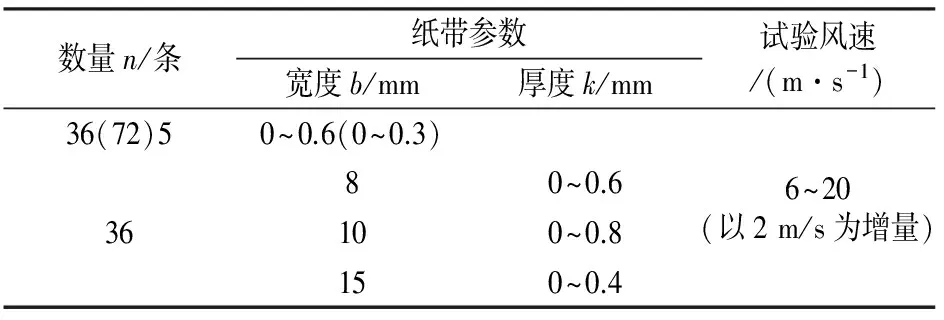
表1 試驗工況

圖2 粗糙度模擬試驗照片

2 參數定義

2.1 壓力系數

在空氣動力學中物體表面的壓力通常采用無量綱壓力系數來表示，冷卻塔表面任意測點i處的風壓系數CPi表示為：

(1)

式中Pi為測點i處的壓力，以指向結構表面為正，離開為負；P∞為參考高度處的來流靜壓；ρ為空氣密度，取ρ=1.225kg/m3；Vi為測點i高度處來流風速.

2.2 風壓曲線特征值

要研究粗糙度對風壓分布的影響，首先要找到能準確描述風壓分布曲線特征的參數，研究它們和粗糙度大小之間的關系.由于圓截面結構的風壓曲

線關于來流對稱分布，分布曲線可以由一些重要的特征點來描述(圖3)：1)最大正壓系數Cpmax，一般為1.0；2)風壓為零的角度θ0；3)最小負壓系數Cpmin及其發生的角度θmin；4)背壓系數Cpb及其發生的角度θb，這個角度也是分離點的位置，事實上，背壓系數Cpb一直沿圓周角變化，因此很難定義它發生的角度θb，本文定義θmin以后第一個風壓曲線斜率為零的點所在圓周角為θb，背壓系數Cpb取θb～180°各點的平均值.

圖3 風壓曲線特征值

2.3 粗糙度系數

圖4所示為在結構物表面布置粗糙條參數示意圖，其中k為粗糙條高度，b為寬度，s為兩粗糙條中心間距，D為結構的直徑.已有研究大多以k/D衡量粗糙度大小，例如，Buresti(1981)[12]，Shih W C L(1993)[13]，操金鑫(2009)[14]等.事實上這一系數忽略了粗糙條數量的影響，可以想象，當粗糙條數量足夠多以致兩兩相接時，“粗糙塔”變成了“光塔”，只是直徑增大了2k.設結構表面布置的粗糙條數量為n，由于粗糙條通常沿圓周等間距布置，本文定義粗糙度系數如下：

(2)

由式(2)可以看出，k/s不僅包含了k/D，還可以考慮粗糙條數量n的影響，定義更為合理，本文重點分析風壓分布特征值與該系數之間的關系.

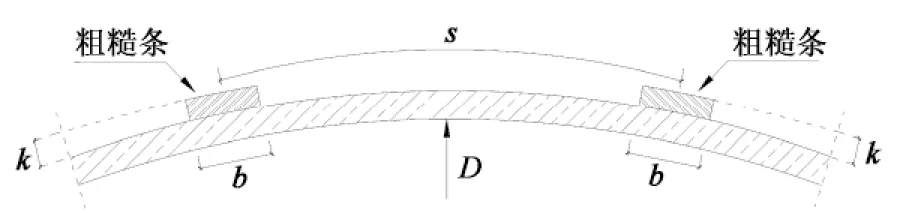
圖4 粗糙條參數示意圖

3 畸變脈動風壓反演修正

測壓試驗中，模型表面的風壓通常需要由一定長度的測壓管道傳輸至壓力傳感器，在這一傳輸過程中，傳感器測得的脈動壓力信號實際上是模型表面真實風壓發生畸變后的信號，反演修正是減小畸變的有效方法之一[15].反演修正的前提是準確獲得測壓管路系統的頻率響應函數，本文在試驗前采用比較法對所用測壓管路系統的頻率響應函數進行了測試[16].風壓測量完成后，采用測得的頻率響應函數對各測點的風壓信號進行反演修正，以保證由脈動風壓測試結果的正確和可靠性.圖5給出的是測量得到的頻率響應函數幅值及相位隨頻率的變化情況，圖6所示為反演修正前后風壓信號在時域和頻域的對比，由圖5和圖6可以看出畸變風壓修正的必要性和反演修正的有效性.

頻率/Hz(a) 幅值

頻率/Hz(b) 相位

時間/s(a) 時域比較

時間/s(b) 頻域比較

4 粗糙條參數對風壓分布的影響

考慮到冷卻塔表面風壓分布具有三維效應，即風壓大小不僅與圓周角有關，還與測點所處高度有關，且由于不同高度處的圓截面半徑不一樣，粗糙條又沿子午向通長布置，故粗糙度系數k/s也隨高度變化，因此本文選取0.55H～0.79H中段各測層的平均風壓曲線作為“代表性曲線”，考察該高度范圍內的平均粗糙度系數對“代表性曲線”特征值的影響.此外，考慮到測試結果的波動性及測點沿環向圓周角的間距較大，為準確比較粗糙度對最小風壓系數、背壓等特征值發生角度的影響，將“代表性曲線”的用最小二乘法進行擬合，擬合的函數公式為中國規范推薦的傅里葉八項式.

4.1 粗糙條寬度b對風壓分布的影響

圖7給出的是典型亞臨界和臨界雷諾數下在保證粗糙條高度k和間距s相同時比較粗糙條寬度b對風壓分布影響的比較結果，從圖中可以看出，不管是在亞臨界還是臨界雷諾數下，不同粗糙條寬度b下的風壓分布基本一致，表明冷卻塔表面風壓分布受粗糙條寬度影響較小.

圓周角/(°)(a) 平均風壓(Re=2.31×105)

圓周角/(°)(b) 脈動風壓(Re=2.31×105)

圓周角/(°)(c) 平均風壓(Re=3.31×105)

圓周角/(°)(d) 脈動風壓(Re=3.31×105)

4.2 粗糙條高度k對風壓分布的影響

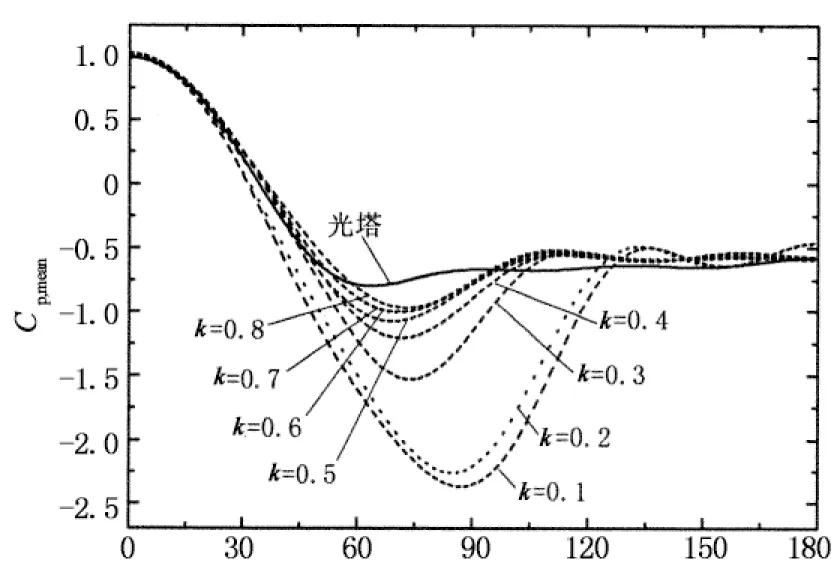
圓周角/(°)(a) 平均風壓(Re=2.31×105)

圓周角/(°)(b) 脈動風壓(Re=2.31×105)

圓周角/(°)(c) 平均風壓(Re=3.31×105)

圓周角/(°)(d) 脈動風壓(Re=3.31×105)

圖8給出的是典型雷諾數下在保證粗糙條寬度b和間距s相同時比較粗糙條高度k對風壓分布影響的比較結果.通過這些圖的比較分析可以看出，對于平均風壓而言，粗糙條高度對正壓區風壓分布和背壓大小影響較小，而負壓區風壓分布和背壓穩定區寬度受它影響較大；由于試驗雷諾數較小，光塔的繞流特性屬于亞臨界狀態(Re=2.31×105)或剛進入臨界狀態(Re=3.31×105)，表面粗糙度一旦增大后，例如k=0.1，繞流特性立即進入臨界狀態，最小負壓系數幅值達到最大值，背壓穩定區寬度減小，此后，隨著粗糙條高度的進一步增加，繞流特性進入超臨界或高超臨界，最小負壓系數幅值減小，背壓穩定區寬度增大，當粗糙度增大至一定程度后，模型表面的繞流特性已經穩定，風壓分布特征基本不再隨粗糙條高度變化，故粗糙條高度的增大效果類似于雷諾數增加；對于脈動風壓，峰值基本隨粗糙條高度的增大而減小.Ribeiro[17]認為脈動風壓主要來源于來流湍流和結構在橫風向的漩渦脫落，且±90°圓周角附近的脈動風壓主要由漩渦脫落貢獻，由于來流湍流和脫落漩渦的相互作用，會導致渦旋強度及穩定性減弱，使得該區域的脈動風壓減小.由于增大表面粗糙度的本質作用在于誘發邊界層提前轉捩，促使邊界層由層流分離轉變為湍流分離，結合Ribeiro的觀點可知，粗糙條高度k越大，其產生的特征湍流強度越大，使得脈動風壓峰值減小，因此在雷諾數效應模擬過程中粗糙條高度不宜過大.

4.3 粗糙條間距s對風壓分布的影響

圖9給出的是在亞臨界和臨界繞流狀態下保證粗糙條高度k和寬度b一致時比較粗糙條間距s對風壓分布影響的比較結果，其中間距s的變化通過改變粗糙條的數量n實現.通過這些圖的對比分析可以發現，不同粗糙條數量下的平均、脈動風壓分布差別較大，并以負壓區的平均風壓尤為顯著；當n=36的風壓分布呈亞臨界繞流特性時，n=72的繞流特性則開始進入臨界區域，最小平均風壓系數和背壓穩定區寬度均顯著減小；當n=36的表面繞流特性呈臨界狀態時，n=72的最小負壓系數幅值減小，背壓穩定區寬度增大，繞流特性向高超臨界過渡.綜上所述，粗糙條數量n大時，表面粗糙度較大.

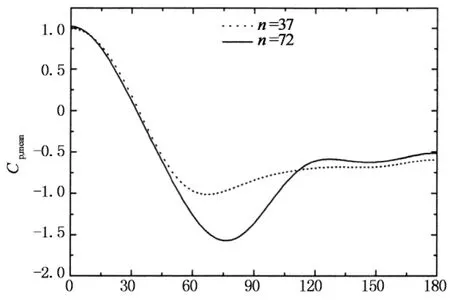
圓周角/(°)(a) 平均風壓(Re=2.31×105)

圓周角/(°)(b) 脈動風壓(Re=2.31×105)

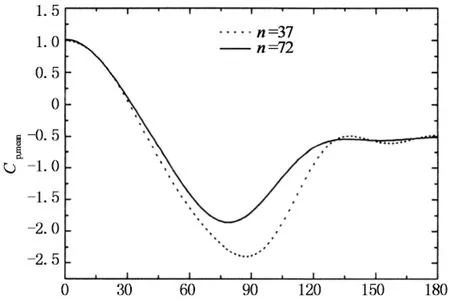
圓周角/(°)(c) 平均風壓(Re=3.31×105)

圓周角/(°)(d) 脈動風壓(Re=3.31×105)

事實上，當結構表面粗糙條數量不是太大以致粗糙條沒有兩兩相接時，可以直觀的想象，當粗糙條高度k和寬度b一致時，肯定是粗糙條數量n較大時的粗糙度大，這進一步表明粗糙度系數k/D并不能完全描述粗糙度大小，粗糙度大小還與粗糙條數量n相關.

5 風壓曲線特征值與粗糙度系數的關系

5.1 粗糙度系數的驗證

為進一步驗證粗糙度系數k/s能否較準確描述粗糙度大小，圖10給出的是在典型亞臨界和臨界雷諾數下保證粗糙條寬度b和粗糙度系數k/s一致時，比較粗糙條數量n對風壓分布影響的比較結果，通過這些圖的對比分析可以看出，不管是在亞臨界還是臨界雷諾數下，當粗糙度系數k/s一致時，盡管兩種工況的粗糙條數量n與厚度k不同，但它們的平均風壓基本一致，n=72時的脈動風壓峰值略大于n=36，其原因在于粗糙條數量大時厚度k較小，而脈動風壓峰值與粗糙條高度k呈反比，這進一步表明通過增大模型表面粗糙度對雷諾數效應補償進行補償時，粗糙條高度不宜過大.由于圖中比較的兩種工況粗糙條數量n不同(即間距s不同)而k/s一致，因此粗糙條數量n大時，厚度k較小，反之，粗糙條數量較少時，厚度k較大，即兩種工況的粗糙條高度k和間距s都不一樣，由此可見，粗糙度大小不能單一以粗糙條高度k或間距s來描述，粗糙度系數k/s才是準確衡量粗糙度大小的重要參數.

圓周角/(°)(a) 平均風壓(Re=2.31×105)

圓周角/(°)(b) 脈動風壓(Re=2.31×105)

圓周角/(°)(c) 平均風壓(Re=3.31×105)

圓周角/(°)(d) 脈動風壓(Re=3.31×105)

5.2 風壓曲線特征值與k/s的關系

圖11給出的是風壓分布曲線特征值隨粗糙度系數k/s的變化曲線，需要說明的是，由于本文的試驗雷諾數較小，當粗糙度小于某一值時，風壓分布還隨雷諾數的增加而變化，表明模型表面的繞流特性尚未進入“自準區”，此時得到的特征值結果特別是最小負壓系數Cpmin意義不大，因此僅給出繞流特性進入“自準區”即風壓分布不再隨雷諾數的增加而變化時的結果.從圖11(a)可以看出，最小負壓系數Cpmin的幅值隨粗糙度系數k/s的增大而略微減小，且當k/s>0.028后，|Cpmin|基本不再變化，大小約為1.0，二者大致存在以下關系：

(3)

如圖11(b)和(c)所示，當繞流特性進入“自準區”后，θb,θ0,θmin及Cpb等參數基本不隨粗糙度變化(這與高超臨界雷諾數下繞流特性穩定的特征相符)，分別約為90°,37°,72°和-0.52.

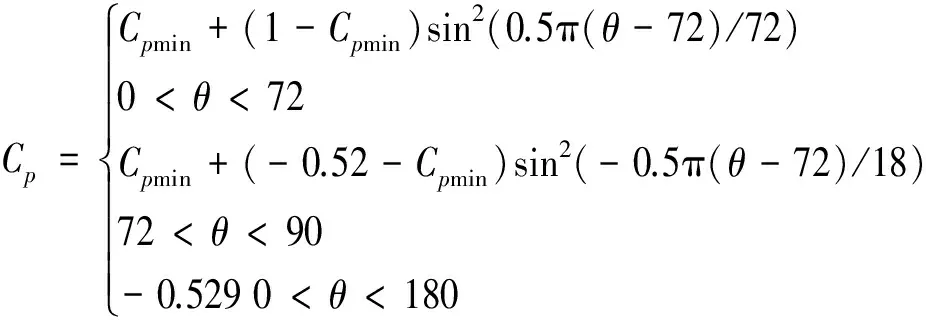
(4)

k/s(a) 最小負壓系數Cpmin

k/s(b) 特征角度

k/s(c) 背壓系數Cpb

5.3 驗 證

國內加肋塔較少，以文獻[19]報導的德國Weisweiler塔為例，其外表面設有52條寬8 cm、高1.8 cm的子午向肋條，喉部直徑為44.6 m，由此計算得到喉部的粗糙度系數k/s=0.067.由于它大于本次試驗的最大粗糙度系數0.03，超出了式(3)的適用范圍，故不能直接用該式計算Cpmin，但由圖11(a)可知，當k/s>0.04后，最小負壓系數Cpmin基本不變，約為-1.0，因此取Cpmin=-1.0，進而由式(4)可近似計算得到它的風壓分布，計算結果與實測結果比較如圖12所示，可以看出，二者除在背壓區有點差異外(背壓差異可能是由于塔型不同引起的，例如李鵬飛等的試驗結果約為-0.50[20]、鮑侃袁的測試結果為-0.31[21]等)，其它圓周角處吻合良好，表明本文推薦的風壓分布近似計算方法可以應用于指導實際冷卻塔工程設計.

圓周角/(°)

6 結 論

本文通過剛性模型測壓試驗分析表面粗糙度對冷卻塔風壓分布的影響，得到以下主要結論：

1)粗糙條寬度b對風壓分布影響較小，而粗糙條高度k和數量n影響較大，粗糙度系數k/s能較準確描述粗糙度大小；當k/s一致時，不同粗糙條數量n與高度k組合下的平均風壓基本一致，但高度大的脈動風壓小.

2)粗糙度對正壓分布和背壓大小影響較小，而負壓區風壓分布和背壓穩定區寬度受它影響較大，其中以最小負壓系數幅值最為顯著；最小負壓系數幅值、脈動風壓系數峰值隨粗糙度的增大而減小，背壓穩定區寬度則略有擴大.

3)由于粗糙條能誘發邊界層提前轉捩，促使邊界層由層流分離轉變為湍流分離，通過增大模型表面粗糙度能有效地在較低雷諾數條件下實現高雷諾數下的平均風壓分布，但脈動風壓模擬的準確性有待大型冷卻塔風壓實測結果的驗證.

[1] 鄒云峰, 牛華偉, 陳政清. 基于完全氣動彈性模型的冷卻塔干擾效應風洞試驗研究[J]. 湖南大學學報: 自然科學版, 2013, 40(12):1-7.

ZOU Yun-feng, NIU Hua-wei, CHEN Zheng-qing. Wind tunnel test on wind-induced interference effect of cooling towers based on full aero-elastic model[J]. Journal of Hunan University: Natural Sciences, 2013, 40(12):1-7.(In Chinese)

[2] 柯世堂, 候憲安, 姚友成, 等. 強風作用下大型雙曲冷卻塔風致振動參數分析[J]. 湖南大學學報: 自然科學版, 2013, 40(10):32-37.

KE Shi-tang, HOU Xian-an, YAO You-cheng,etal. Parameter analysis of wind-induced vibration for large hyperbolic cooling towers under strong wind loads[J]. Journal of Hunan University: Natural Sciences, 2013, 40(10):32-37. (In Chinese)

[3] NIEMANN H J, ZERNA W. Impact of research on development of large cooling towers[J]. Journal of Engineering Structures, 1986, 8: 74-86.

[4] 鄒云峰, 牛華偉, 陳政清. 基于完全氣動彈性模型的冷卻塔風致響應風洞試驗研究[J]. 建筑結構學報, 2013, 34(6):60-67.

ZOU Yun-feng, NIU Hua-wei, CHEN Zheng-qing. Wind tunnel test on wind-induced response of cooling tower based on full aero-elastic model[J]. Journal of Building Structures, 2013, 34(6):60-67. (In Chinese)

[5] ARMITT J. Eigenvector analysis of pressure fluctuations on the West Burton instrumented cooling tower[R]. London: Central Electricity Research Laboratories, 1968: 114-168.

[6] FARELL C, GUVEN O, MAISCH F. Mean wind loading on rough-walled cooling towers[J]. Journal of the Engineering Mechanics Division, ASCE, 1976, 102(6): 1059-1081.

[7] NIEMANN H J. Wind effects on cooling-tower shells[J]. Journal of the Structural Division, ASCE, 1980, 106(ST3): 643-661.

[8] 孫天風, 周良茂. 無肋雙曲線型冷卻塔風壓分布的全尺寸測量和風洞研究[J]. 空氣動力學學報, 1983, 4: 68-76.

SUN Tian-feng, ZHOU Liang-mao. A full-scale and wind-tunnel study of wind pressure distribution around a ribless hyperbolic cooling tower[J]. Acta Aerodynamica Sinica, 1983, 4: 68-76. (In Chinese)

[9] 劉天成, 趙林, 丁志斌. 圓形截面冷卻塔不同表面粗糙度時繞流特性的試驗研究[J]. 工業建筑, 2006, 36(增刊): 301-304.

LIU Tian-cheng, ZHAO Lin, DING Zhi-bin. Test research of flow feature for hyperbolic circular section cooling tower with different superficial roughness[J]. Industrial Construction, 2006, 36(S1): 301-304. (In Chinese)

[10]沈國輝, 余關鵬, 孫炳楠, 等. 模型表面粗糙度對冷卻塔風荷載的影響[J]. 工程力學, 2011, 28(3): 86-93.

SHEN Guo-hui, YU Guan-peng, SUN Bing-nan,etal. The influence of modal surface roughness on wind loads of cooling towers[J]. Engineering Mechanics,2011, 28(3): 86-93. (In Chinese)

[11]董國朝, 陳政清, 羅建輝, 等. 冷卻塔混凝土粗糙度對平均風壓系數的影響[J]. 湖南大學學報:自然科學版, 2011, 38(7): 6-12.

DONG Guo-chao, CHEN Zheng-qing, LUO Jian-hui,etal. Effect of surface roughness on the mean pressure coefficient of concrete cooling tower[J]. Journal of Hunan University:Natural Sciences, 2011, 38(7): 6-12. (In Chinese)

[12]BURESTI G. The effect of surface roughness on the flow regime around circular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8: 105-114.

[13]SHIH W C L, WANG C, COLES D,etal. Experiments on flow past rough circular cylinders at large Reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49: 351-368.

[14]操金鑫, 趙林, 葛耀君, 等. 雙曲線圓截面建筑結構雷諾數效應模擬實踐[J]. 實驗流體力學, 2009, 25(4): 46-50.

CAO Jin-xin, ZHAO Lin, GE Yao-jun,etal. Practices on simulation of Reynolds number effects for the hyperbolic circular section structures[J]. Journal of Experiments in Fluid Mechanics, 2009, 25(4): 46-50. (In Chinese)

[15]SURRY D, DJAKOVICH D. Fluctuating pressures on models of tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 58: 81-112.

[16]鄒云峰. 巨型冷卻塔群的風效應及其風洞試驗方法研究[D]. 長沙: 湖南大學土木工程學院, 2013: 29-34.

ZOU Yun-feng. Study on wind effects and wind-tunnel test method for super large cooling towers group[D]. Changsha:College of Civil Engineering, Hunan University, 2013:29-34. (In Chinese)

[17]RIBEIRO J L D. Effects of surface roughness on the two-dimensional flow past circular cylinders Ⅱ: fluctuating forces and pressures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1991, 37: 311-326.

[18]YEUNG W W H. Similarity study on mean pressure distribution of cylindrical and spherical bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95: 253-266.

[19]NIEMANN H J. Wind pressure measurements on cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1973, 1: 265-281.

[20]李鵬飛, 趙林, 葛耀君, 等. 超大型冷卻塔風荷載特性風洞試驗研究[J]. 工程力學, 2008, 25(6): 60-67.

LI Peng-fei, ZHAO Lin, GE Yao-jun,etal. Investigation on wind load characteristics for super large cooling tower in wind tunnel[J]. Engineering Mechanics, 2008, 25(6): 60-67. (In Chinese)

[21]鮑侃袁. 大型雙曲冷卻塔的風荷載和風致響應理論分析與試驗研究[D]. 杭州: 浙江大學建筑工程學院, 2009: 33-36.

BAO Kan-yuan. Theory analysis and experimental study on wind load and wind-induced response for large hyperbolic cooling tower[D]. Hangzhou: Department of Civil Engineering,Zhejiang University, 2009: 33-36. (In Chinese)

Influence of Modal Surface Roughness on Wind Pressure Distribution of Hyperbolic Cooling Tower

ZOU Yun-feng1,2,3, HE Xu-hui1,2?, WANG Han-feng1,2, TAN Li-xin3, NIU Hua-wei4

(1．School of Civil Engineering, Central South Univ, Changsha, Hunan 410075, China;2．National Engineering Laboratory for High Speed Railway Construction, Changsha, Hunan 410075, China;3．China Construction Fifth Engineering Division Co Ltd., Changsha, Hunan 410004, China;4．Wind Engineering Research Center， Hunan Univ, Changsha, Hunan 410082, China)

The wind pressure distribution of cooling towers with different rough strip parameters was tested, and the influence of roughness on both mean and fluctuating wind pressure was investigated. The experiment results show that the width of rough strip has little effect on the distribution of wind pressure, while the height and number have a greater impact, and the roughness coefficientk/scan describe the size of roughness accurately. Even though the numbernand heightkof rough strip is different, as long as the roughness coefficientk/sis consistent, the mean pressure distribution is basically the same, but the peak fluctuating pressure is smaller with higher height of rough strip. Furthermore, roughness has little effect on both the distribution of positive pressure and the size of back pressure. However, the amplitude of the smallest negative pressure coefficient and the peak fluctuating pressure decrease with the increase of roughness, while the width of back pressure expands slightly. Although the mean pressure at high Reynolds number can be simulated effectively at low Reynolds number by increasing surface roughness, the simulation accuracy of fluctuating pressure should be checked with field tests in the future.

cooling tower; surface roughness; wind pressure distribution; wind tunnel test

1674-2974(2015)07-0016-09

2014-09-10

國家自然科學基金資助項目(51178471,51322808) ,National Natural Science Foundation of China(51178471,51322808) ；中國博士后科學基金資助項目(2014M562133); 教育部新世紀優秀人才支持計劃(NCET-12-0550)

鄒云峰(1984-)，男，湖南邵陽人，中南大學講師，博士

?通訊聯系人，E-mail:xuhuihe@csu.edu.cn

TU311.3；V211.7

A