GPS接收機模糊搜索粗時定位方法*

靖守讓，劉文祥，吳 鵬，孫廣富

(國防科技大學電子科學與工程學院，湖南長沙410073)

全球定位系統(Global Positioning System，GPS)能提供全球范圍內的定位服務。傳統GPS接收機為實現定位需要通過信號捕獲、信號跟蹤、位同步、幀同步以及定位解算等幾個步驟［1］。信號捕獲和跟蹤后用戶可以獲得碼相位測量值;位同步后能夠獲得20ms內的偽距值，幀同步后能夠獲取完整的信號發射時間。GPS衛星的偽距變化率最大值約為800m/s，因此利用優于10ms的時間精度計算衛星位置產生的偽距偏差小于8m。對于標準單點定位的首次定位而言，這通常是可以接受的，因此通常將10ms作為導航定位時的時間精度界限。一般將接收機時間精度優于10ms的定位稱為精時定位，相反稱為粗時定位［2］。傳統接收機通常在完成幀同步后獲得精確時間。但是幀同步一般需要經歷1～2幀電文，對GPS L1 C/A信號為6～12s。同時在弱信號等惡劣條件下，由于解調電文數據的比特誤碼，可能導致遲遲不能實現幀同步。

為提高首次定位時間，Peterson等在文獻［3］中針對粗時定位問題首次提出了5狀態方程。van Diggelen對粗時定位算法進行了詳細描述，并針對文獻［3］方法中共有偏差引起的毫秒翻轉誤差問題提出了用于解決毫秒整數模糊問題的van Diggelen技術［4］。van Diggelen技術能有效解決毫秒整數模糊問題，但是免時定位算法要求用戶概略位置和粗略時間對偽距影響小于150km。因此針對GPS的粗時定位算法的研究主要集中在概略位置獲取上。文獻［5］在概略位置未知的情況下采用格網搜索的方法實現接收機定位，但是由于待搜索空間較大，導致計算量太大。文獻［6］對聯合多普勒的粗時定位方法進行了研究，即利用多普勒觀測值估算接收機概略位置后使用免時定位方法進行定位。但是該方法適用于靜止或者低動態用戶，否則將導致多普勒定位誤差超出毫秒整數模糊度恢復約束。文獻［7］通過時間搜索的方法將時間精度要求擴展到12h，并針對多普勒定位結果不可靠時提出了模糊搜索的方法，從而擴展聯合多普勒定位對用戶速度的限制。但是該方法沒有從根本上解決多普勒定位對用戶速度約束的局限性問題，同時極大地增加計算量。文獻［8］為減小搜索空間，針對地表用戶從時間維進行搜索，但是需要微秒級的高精度的時鐘輔助。上述方法均針對碼捕獲階段展開討論，而隨著技術的發展，即使在弱信號環境下，仍能實現接近100%的信號位同步［9］。

1 基于偽距殘余檢驗的粗時定位方法

1.1 概略位置計算

非輔助的傳統GPS接收機需要經過碼捕獲、相位鎖定、位同步、幀同步等階段后才能通過電文獲取周內秒時間(Time of Week，TOW)，從而獲得信號發射時刻［10］。在位同步后能夠獲得亞20mm的偽距值。因此在實現位同步后，第i顆衛星的偽距可以表示為:

其中:ρi表示偽距值為本地時間為由本地時間計算的信號發射時間;)表示時刻計算得到的衛星i的位置在時刻用戶位置的空間距離為接收機鐘差，單位為表示本地時間的絕對偏差;Δr(δtr)表示由于本地時間不準確，計算衛星位置偏差引起的空間距離誤差;εi表示誤差項;Ni，20ms表示20ms的偽距模糊度;L20ms為20ms距離，約為6000km表示亞20ms偽距測量值。

各顆可見的GPS衛星離地面上接收機的距離互不相等，最短的距離約為20 192km，最長的距離可達25 785km。衛星的傳播時間分布在67～86ms之間［11］。由于信號在位同步后能夠得到亞20ms偽距。因此，在位同步后可以構建偽距模糊組合用于解算初值，并根據定位后的偽距殘余選擇最合理的偽距模糊組合和粗定位結果用于后續的免時定位。位同步后的偽距模糊組合可以采用如下兩種方式構建:各衛星模糊互相獨立，模糊值只有2種，同時各衛星模糊度相同時認為是同一種情況;以某顆衛星為基準，其他衛星模糊度變為3種情況。在無其他約束情況下，兩種方法構建偽距模糊組合的個數與衛星數的關系見表1。

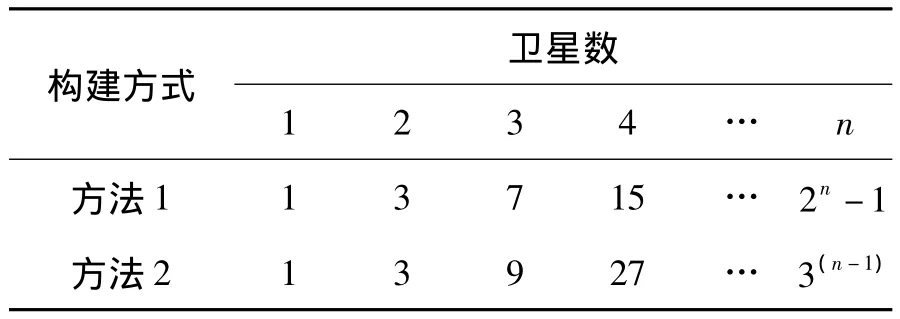
表1 偽距模糊組合數與衛星數關系Tab.1 Relationship between number of satellites and number of ambiguity combination

由于對地面用戶，衛星的傳播時間分布在67～86ms之間，即任意兩顆衛星間的偽距差值小于20ms。因此，在增加偽距之差小于20ms約束后，能夠有效剔除不合理組合。

假設n顆衛星的亞20ms偽距從大到小排列的組合為，則在偽距之差小于20ms約束的前提下模糊組合形式為否則偽距之差會出現超出20ms的情況。因此在增加20ms約束后采用上述兩種方法遍歷偽距模糊獲得的有效組合數相等，且均等于衛星數。

通常而言，對于采用實時時鐘(Real Time Clock，RTC)提供時間保持的接收機能夠在幾周內保持本地時間精度在數秒以內［12］。而GPS衛星偽距變化率的最大值約為800m/s。因此，當本地時間精度保持在數秒，即使在最差情況下，由衛星位置計算引起的偽距誤差也僅為數千米，遠小于20ms模糊錯誤(甚至碼捕獲后的毫秒整數模糊)帶來的誤差。因此可以忽略式(1)中直接進行最小二乘解算，在正確的模糊組合下定位后的偽距殘差會小于存在模糊錯誤的偽距殘差。對于給定的Ni，20ms，式(1)可以寫為如式(2)的形式，此方程與傳統的衛星觀測方程一致，可以直接使用最小二乘迭代解算用戶位置。

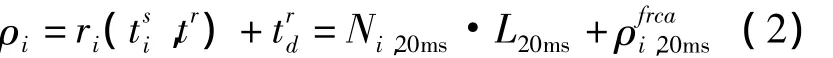
由于隨著衛星數的增加偽距模糊組合數也逐漸增加，為了減小計算量，可以采用在n顆衛星中選出m顆衛星進行粗定位獲取概略位置和正確的偽距模糊組合。同時由于本地時間不準確，導致計算衛星位置出現偏差，即使在正確的偽距模糊組合時仍存在數百甚至數千米的誤差。因此在選取m顆衛星時，可以選擇幾何精度因子(Geometric Dilution Of Precision，GDOP)較小的星座組合。通常選擇4顆衛星即可估計出用戶的概略位置。

定位后，衛星的偽距殘差可以通過式(3)計算，其中mod(·)表示取模操作。

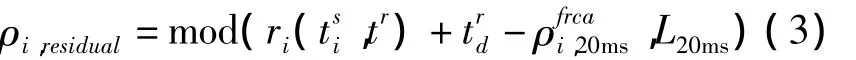
當本地時間偏差較小時，衛星位置計算誤差造成的影響遠小于偽距模糊錯誤帶來的影響。正確的偽距模糊的定位誤差較小，計算得到的模糊偽距內殘余也會相對較小。因此，計算用戶概略位置和模糊組合的具體步驟為:

1)在n顆衛星中選擇m顆GDOP較好的衛星;

2)構建m顆衛星的偽距模糊組合，遍歷所有有效組合并進行最小二乘解算，計算用戶位置和m顆衛星的偽距殘余;

3)根據每次的定位結果，計算其他n－m顆衛星的20ms模糊以及偽距殘余;

4)結合步驟2、步驟3獲取的n顆衛星偽距殘余，計算n顆衛星偽距殘余均方根(Root Mean Square，RMS)。并以偽距殘余均方根最小為準則選出最合理的偽距模糊組合和用戶概略位置。

以國際GNSS服務(International GNSS Service，IGS)組織的mars測站L1頻點數據進行分析實驗。某一時刻觀測到7顆衛星，星空圖如圖1所示。

圖1 可視衛星的星空圖Fig.1 Sky charts of visual satellite

選取4顆衛星計算概略位置時，20ms模糊組合僅包含以下四種情況:［3，3，3，3］，［3，3，3，4］，［3，3，4，4］，［3，4，4，4］。其中組合1為正確情況。本算例中選擇出的4顆衛星為2，24，25，31。并分別拉偏本地時間從0s到10s，解算后得到的偽距殘差均方根見表2。

由表2可知，鐘差偏差較小時由正確的偽距模糊組合解算得到的偽距殘余均方根明顯小于錯誤情況。其中鐘差為0時偽距殘余均方根仍較大是由于在粗解算時未對電離層延遲、對流層延遲等誤差項進行修正，僅對對定位影響較大的衛星鐘差進行了修正。

表2 不同模糊組合下的偽距殘余均方根Tab.2 RMS of pseudorange residual under different ambiguity combination

1.2 免時定位方法

當獲取用戶概略位置和成功恢復各衛星的模糊組合后，式(1)中未知變量僅包含三維用戶位置、接收機鐘差以及接收機絕對時間偏差。因此可以使用免時定位算法解算用戶位置和時間偏差。免時定位算法的矩陣方程可以表示為:

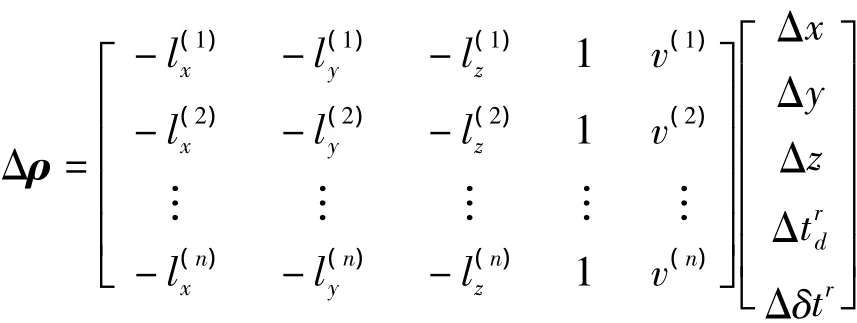
由于免時定位算法存在5個未知量，因此至少使用5顆衛星信息對未知量進行估計。而在本地時間偏差較大時，使用該方法進行粗定位也可能選擇錯誤的偽距模糊組合。因此，為保證最終定位結果的可靠性，在無法確定本地時間精度范圍的情況下，至少需要6顆衛星進行后續的免時定位解算。而且衛星數越多，基于偽距殘余最小準則獲取的偽距模糊組合的可靠性越高。表3給出了mars站在本地時間存在不同偏差的情況下，分別使用5顆星和6顆星進行定位的定位誤差以及定位后的偽距殘余均方根。

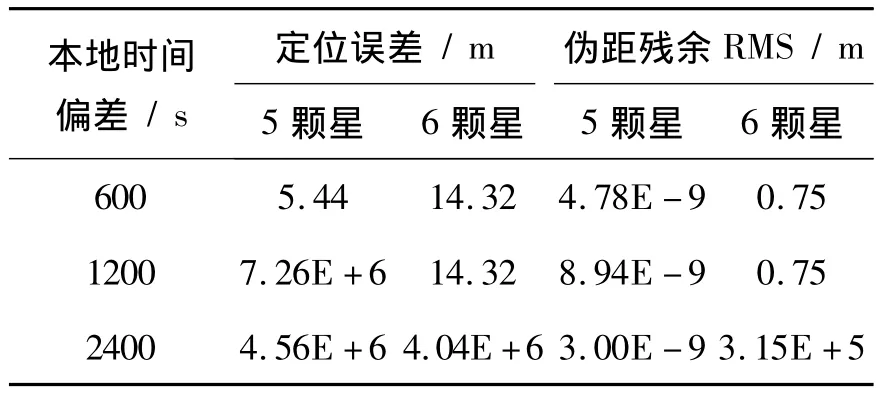
表3 不同衛星數時定位結果Tab.3 Position results with different number of satellites

由表3可知，使用6顆星進行定位時，在定位誤差較大時偽距殘余RMS值同樣比較大，能夠通過偽距殘余RMS值識別定位是否成功。而5顆星時無論定位是否成功，定位后的偽距殘余RMS值均很小。無法通過最終的偽距殘余RMS值判斷最終的定位結果是否正常。

2 實驗與分析

GPS衛星的軌道運行周期為11h58min，星座分布的重復周期為1d［13］。因此利用1d時長的GPS觀測數據進行仿真實驗。使用IGS提供的2014年12月31日11個測站觀測數據進行后續分析實驗，其中測站分布如圖2所示。

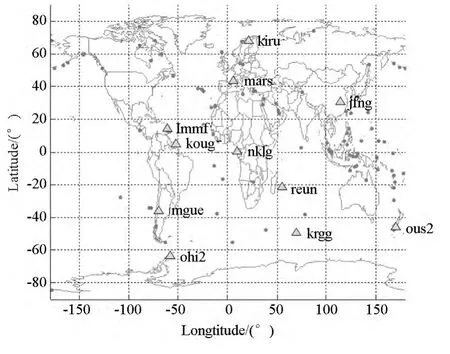
圖2 11個IGS測站分布圖Fig.2 Distribution of 11 IGS stations

在時間拉偏10s的情況下，利用mars測站L1觀測數據，把該粗時定位方法和完整偽距的精時定位方法的誤差進行對比，其可視衛星數如圖3所示。

由圖3可知，粗時定位精度在絕大多數時間與使用完整偽距的精時定位相當，少部分時間粗時定位精度比精時定位精度略差。這是由于免時定位算法存在5維未知量，因此在衛星數較少的情況下通過免時定位算法迭代獲得的本地時間偏差δtr出現誤差從而導致定位精度略差。

11個測站的定位誤差統計結果見表4，其中水平誤差和垂直誤差均指95%的可能性誤差。由表4可知，在概略位置未知時，使用模糊搜索方法能夠實現GPS接收機粗時定位，且定位精度與直接使用完整偽距的定位精度相當。

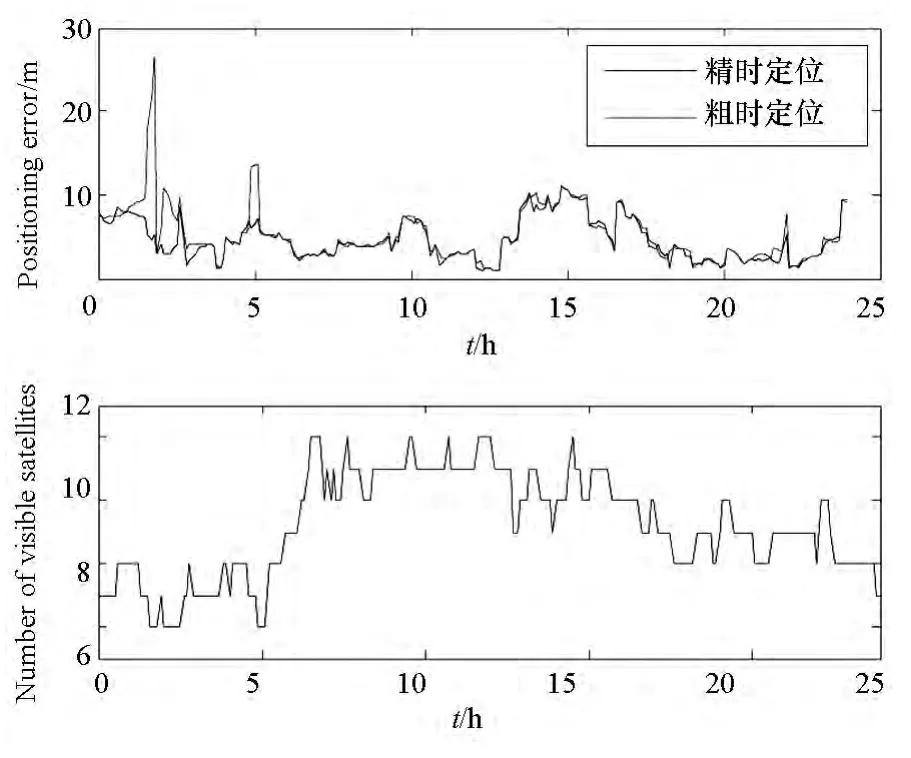
圖3 粗時定位和精時定位結果Fig.3 Result of coarse-time position and precise-time position

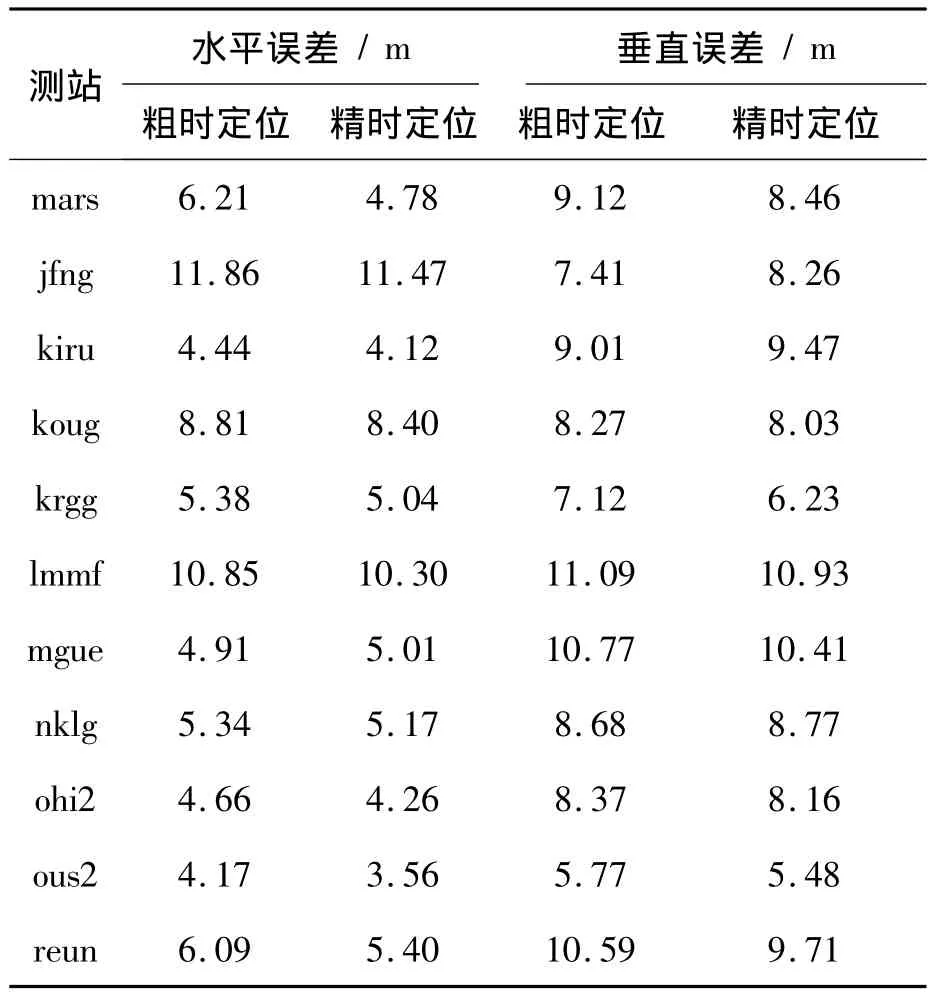
表4 定位誤差統計結果Tab.4 The positioning error statistical results

3 結論

論文提出基于偽距殘余檢驗的粗時定位方法，通過偽距殘余最小均方根準則獲取概略位置和衛星之間的相對偽距。能夠在概略位置完全未知的情況下結合免時定位算法計算得到用戶準確位置。詳細描述了偽距殘余最小均方根準則下的概略位置計算流程和免時定位方法，并使用IGS的11個測站數據驗證了方法的有效性。同時統計結果表明提出的粗時定位方法的定位精度與使用完整偽距信息的定位精度相當。

提出的基于偽距殘余檢驗的GPS接收機粗時定位方法同樣適用碼捕獲后僅獲取亞毫米偽距情況。在此種情況下，隨著衛星數增加，搜索空間將急劇增大。可以采用高程或高精度時鐘輔助等手段減小粗定位時衛星數需求，從而縮小模糊搜索空間。

References)

［1］Kaplan E D，Hegarty C J.Understanding GPS:principles and applications［M］.2nd ed.USA:Artech House，2006.

［2］Van Diggelen F.A-GPS:assisted GPS，GNSS，and SBAS［M］.USA:Artech House，2009.

［3］Peterson B，Hartnett R，Ottoman G.GPS Receiver structures for the urban canyon［C］//Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation，1995:1323－1332.

［4］Van Diggelen F.Method and apparatus for time-free processing of GPS signals［P］.US Patent 6417801，July 9，2002.

［5］Sirola N.Exhaustive global grid search in computing receiver position from modular satellite range measurements［J］.Journal of Physics:Conference Series，2006，52(1):73－82.

［6］Othieno N，Gleason S.Combined Doppler and time free positioning technique for low dynamics receivers［C］//Proceedings of IEEE ION Position Location and Navigation Symposium，2012:60－65.

［7］Chen H W，Wang H S，Chiang Y T，et al.A new coarse-time GPS positioning algorithm using combined Doppler and code-phase measurements［J］.GPS Solutions，2014，18(4):541－551.

［8］Wu P，Jing S R，Liu W X，et al.A quick location method for high dynamic GNSS receiver based on time assistance［J］.International Journal of Computers Communications＆Control，2013，8(5):768－773.

［9］Ren T T，Petovello M.An analysis of maximum likelihood estimation method for bit synchronization and decoding of GPS L1 C/A signals［J］.EURASIP Journal on Advances in Signal Processing，2014:3.

［10］Lannelongue S，Pablos P.Fast acquisition techniques for GPS receivers［C］//Proceedings of the 54th Annual Meeting of the Institute of Navigation，1998:261－269.

［11］謝鋼.GPS原理與接收機設計［M］.北京:電子工業出版社，2009.XIE Gang.Principles of GPS and receiver design［M］.Beijing:Publishing House of Electronics Industry，2009.(in Chinese)

［12］陳亮，咸德勇，劉思慧，等.一種新型高精度低功耗守時芯片［J］.國防科技大學學報，2013，35(3):176－180.CHEN Liang，XIAN Deyong，LIU Sihui，et al.A novel highprecision，low-power time keeping chip［J］.Journal of National University of Defense Technology，2013，35(3):176－180.(in Chinese)

［13］謝鋼.全球導航衛星系統原理——GPS、格洛納斯和伽利略系統［M］.北京:電子工業出版社，2013.XIE Gang.Principles of GNSS:GPS，GLONASS and Galileo［M］.Beijing:Publishing House of Electronics Industry，2013.(in Chinese)