應用多GPU的可壓縮湍流并行計算*

曹文斌，李 樺，謝文佳，張 冉

(國防科技大學航天科學與工程學院，湖南長沙410073)

隨著硬件性能的提高及編程技術的改進，圖形處理器(Graphical Processing Unit，GPU)加速器在高性能計算領域逐漸得到廣泛的應用。在最新公布的超級計算機Top500名單中共有62套系統采用了加速器/協處理器，其中采用GPU加速器有46套，而在最新的Green500名單中前10位的超級計算機均采用了GPU加速器，由此可見GPU加速器在高性能計算中的優勢。在通用計算中NVIDA GPU具有低成本、低功耗、高性能及易編程等優點，非常適合計算密集型應用。發布的CUDA并行編程架構［1］使開發人員能夠在不了解圖形學知識的條件下進行高級語言環境下的GPU編程以高效快速地解決許多復雜計算問題。目前在流體力學領域，已有大量的數值模擬方法針對GPU進行了改造，這其中有計算流體力學(Computational Fluid Dynamics，CFD)、格子玻爾茲曼、直接模擬蒙特卡洛、分子模擬等方法。

湍流一直是CFD領域的難點與熱點，近年來，國內外已有許多學者將GPU計算應用到湍流的數值模擬當中，取得了良好的加速效果。Aaron［2］針對不可壓縮湍流問題，基于Tesla C1060 GPU發展了大渦模擬求解器并給出了實現多GPU并行計算的方法。Cao與Xu等［3］應用高精度求解器在天河－1A系統上實現了多GPU與多CPU的協同并行計算，討論了提高異構系統并行效率的方法。Lin等［4］基于GeForce 560Ti GPU發展了多塊結構網格湍流求解器，利用MPI加OpenMP實現了多GPU的并行計算。Ali等［5］在Tesla S1070多GPU集群上實現了湍流的直接數值模擬，分析了利用零拷貝技術與固定內存技術對提高系統效率的影響。可以發現，在現有的計算流體力學應用中，大多數研究針對的是計算能力較低的設備。而最新的設備(計算能力3.5)更新了硬件架構，例如引入了Hyper－Q，提升了顯存帶寬，增加了可用的寄存器個數等，這就需要研究人員根據最新架構的功能與特點對算法做出相應的調整與改進，以發揮設備的最佳性能，實現更加復雜更大計算規模任務的模擬。研究發展了基于CUDA Fortran的三維定常可壓縮湍流求解器。

1 控制方程

當不考慮外部加熱和徹體力的影響時，三維曲線坐標系下守恒形式的Navier-Stokes方程如下:

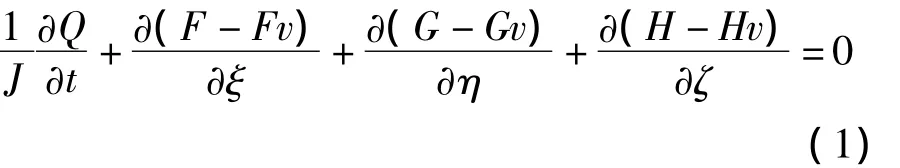
此處Q為守恒變量;J代表曲線坐標系(ξ，η，ζ)與笛卡爾坐標系(x，y，z)之間的雅克比轉換行列式;F，G，H為曲線坐標系三個方向的無黏通量;Fv，Gv，Hv代表黏性通量。考慮k－ωSST湍流模型時，除了添加兩個包含源項的湍流方程之外，方程(1)的形式不變，此時黏性系數μ由層流黏性系數μL及渦黏性系數μT兩部分組成，相應的μ/pr關系式如下:

式中，μL通過Sutherland公式得到，μT由湍流模型給出，prL為層流普朗特數，對于空氣可取0.72，prT為湍流普朗特數，一般取0.9。當不考慮湍流模型時，渦黏性系數為0。湍流模型的具體公式及參數設置見文獻［6］。

對控制方程(1)運用基于單元中心型的有限體積法求解，無黏通量采用AUSMPW+格式［7］，通過MUSCL方法選用Vanleer平均限制器對原始變量進行空間重構達到二階精度，黏性通量采用高斯積分公式進行求解，時間推進為單步顯式方法。

2 GPU算法優化方法

由于GPU程序優化與硬件的體系結構及軟件環境密切相關，因此本節首先給出計算平臺配置情況。計算軟件環境如下:CPU代碼用Fortran語言編寫，GPU代碼為CUDA Fortran語言;兩個版本的代碼均由PGI Fortran 13.10編譯器［8］加OpenMPI庫編譯，優化參數設置使兩種設備的性能達到最佳;GPU計算使用單精度。硬件配置如下:每個節點配置一塊CPU與一塊GPU及64G內存，節點間通信采用鏈路匯聚的千兆以太網絡;運行的CPU為Intel Xeon E5－2670@2.6 GHz，超線程關閉;測試使用的GPU為6G顯存的NVIDA GTX TITAN Black。

2.1 單GPU算法優化

CFD迭代求解過程主要包括邊界條件更新、通量計算、時間步長與源項計算及流場更新四個步驟。其中通量計算是決定求解器整體運行速度的主要因素，通常是優化的重點。不管是無黏通量還是黏性通量，在GPU上它們的計算都是首先從全局內存中輸入網格單元的幾何量和原始變量;其次通過空間格式得到單元界面通量;最后將通量或通量差結果輸出至全局內存中。因此從優化方面考慮，可以將通量計算方法分為兩類算法:輸入優化(算法1)與輸出優化(算法2)。為了分析對比，將不進行優化的算法定義為全局內存方法。

算法1的具體流程如下所示。為了節省全局內存開銷，界面通量數組f被多次重復使用。

算法1輸入優化Alg.1 Input optimization

算法1中每個內核在讀取數據階段，均使用了下面介紹的優化方法。由于每個線程都需要用到相鄰線程的信息，例如在計算ξ方向無黏通量Fi－1/2時涉及i－2，i－1，i，i+1共4個網格單元的原始變量值，若應用全局內存方法(將數據從全局內存直接讀入寄存器)讀取這些信息，將會產生大量的重復訪問。為了提高帶寬利用率降低訪問延遲，常用的辦法就是使用共享內存來緩解對全局內存的重復訪問，具體使用方法見文獻［9］。文獻［10］給出了無黏通量計算的一種更高效的方法，即使用寄存器移位技術達到減少重復訪問的目的，同時還給出了黏性通量的優化方法。本文求解器在算法1中采用文獻［10］的方法進行優化。圖1給了大小為1923的網格在不同GPU架構下的通量計算時間對比，與全局內存方法相比，算法1在計算能力2.0的Tesla C2050上獲得了25.1%的性能提升，而在計算能力3.5的GTX TITAN Black上僅有8.3%的提升。可以看出，對于重復數據的讀取，在顯存帶寬有了顯著提升并引入了L2緩存的計算能力3.5的設備上，使用優化加速技術并不能取得明顯的加速效果。

算法2對結果輸出做優化，具體的流程如下

算法2輸出優化Alg.2 Output optimization

可以看出，算法2在輸出階段利用共享內存消除了中間變量f的使用，這樣既節省了全局內存消耗又避免了對全局變量的額外讀寫操作，同時所有內核不存在數據依賴性可并發執行。因為存儲于網格中心的右端項RHS是通過兩個界面通量做差值得到，所以每個線程塊中計算得到的RHS個數少于線程塊中的線程數，這樣在每個線程塊中除了需要引入新的分支語句，還需要在相鄰線程塊的邊界處進行冗余計算。分支語句的增多與冗余計算的存在使得算法1中的輸入優化技術在算法2中不但不能發揮應有的加速效果而且會引起性能的下降。因此算法2在讀入數據階段不進行優化，即應用全局內存方法讀取數據。由圖1可以看出，算法2非常適合計算能力3.5的GTX TITAN Black，與全局內存方法相比，獲得了18%的速度提升。

除了上述優化方法外，一些常規的優化方法在本文中均有應用，如全局變量按數組結構體方式儲存，盡量避免束內分支，盡可能減少中間變量以降低寄存器使用量，減少PCIe數據傳輸，采用樹形規約算法執行殘值加和操作。所有計算配置的線程塊大小為32×8×1。

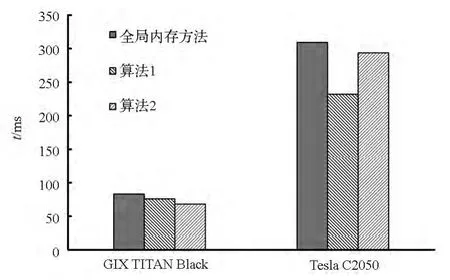
圖1 不同算法計算時間對比Fig.1 Computing time of different algorithms

2.2 多GPU并行算法

在求解器進行基于區域分解的并行計算過程中，相鄰網格區域在邊界處需要對原始變量進行數據交換。當多區網格位于同一塊GPU中，此時為內部邊界，可以在GPU中實現直接數據交換(求解器支持一個MPI進程處理多區結構網格);當相鄰網格區域位于不同GPU時，需要先將一塊GPU的邊界數據通過PCIe總線傳輸至主機端，然后調用MPI進行交換，最后再通過PCIe傳輸至另一塊GPU。雖然已有GPUDirect技術實現GPU間的直接通信，但是現有系統的通信設備并不具有該功能，而升級設備成本又很高，因此提高現有系統的并行計算效率具有很大的實用價值。計算能力3.5的GPU引入了一個名為Hyper－Q的重要功能，它允許32個獨立的CUDA流隊列同時工作。利用該功能，可以實現GPU計算與邊界數據交換的高度重疊。具體實現過程如圖2所示。

首先，創建N個CUDA流(N≤32)。流1與流2分別用于所有區域的ζ方向內點無黏通量計算與內部邊界更新等內核的啟動。流3至流N負責所有需要進行數據交換的邊界處理，這其中包括GPU上數據整理(將邊界數據整理至預先分配好的連續儲存空間中)，設備端至主機端的異步傳輸(Device to Host，D2H)，主機端至設備端的異步傳輸(Host to Device，H2D)及GPU邊界數據更新。其次，所有流啟動相應的內核執行，流3至流N的每個流在啟動MPI非阻塞發送之前應用CUDA流查詢函數確保D2H傳輸已完成，在啟動H2D傳輸之前需等待MPI非阻塞接受完成。由于Hyper-Q特性允許流與流之間的操作互不阻塞，所以流1與流2對應的多個內核從一開始就與數據整理內核同時啟動，內核的執行與PCIe傳輸及MPI數據交換同步進行，多個D2H或H2D傳輸可以同時存在，MPI非阻塞通信與D2H傳輸在不同流之間重疊。最后調用流同步完成所有流的內核執行。圖中流1雖然只包含了ζ方向的內點無黏通量計算，若它的計算時間小于數據交換所需要的時間，可以將η方向的相應計算加入流隊列中，以實現GPU計算與邊界數據交換的高度重疊。

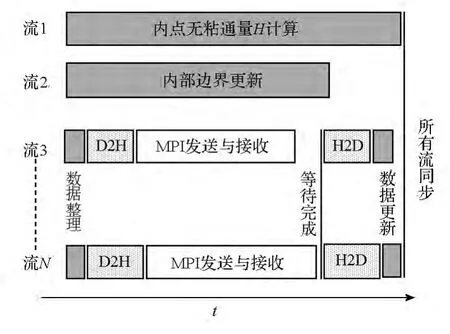
圖2 多GPU并行算法Fig.2 Multi-GPU parallel algorithm

3 算例分析

3.1 超聲速進氣道

Reinartz等［11］對混合壓縮進氣道進行了大量的數值與實驗研究，獲得了清晰的流場結構與進氣道壁面壓力分布。圖3所示為擴張段以前的進氣道構型，上壓縮面的壓縮角δ2為21.5°，下楔面的傾斜角δ3為9.5°，擴張段的擴張角δ4為5°，隔離段的長度l為79.3mm，高度h為15mm，進氣道總長為400mm，寬為52mm。

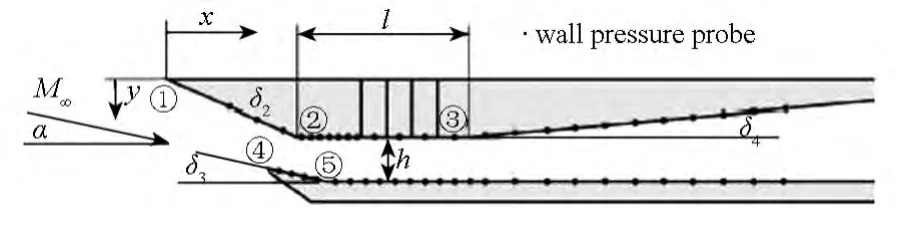
圖3 進氣道模型示意圖Fig.3 Schematic of the inlet model

進氣道流動計算條件為:攻角α為－10°，馬赫數M∞為2.41，總壓540kPa，總溫305K。由于實驗時間較長，可認為壁面已達到熱傳導平衡狀態，因此計算時壁面采用絕熱條件假設。采用單區結構網格對進氣道流場區域進行離散。為了測定GPU在不同網格量下的性能表現，設置了多套網格，其中最粗的網格由256×48×64(流向×法向×展向)個網格點組成，在此基礎上將前兩個方向的網格點數量分別加密得到其余的網格，最密的網格其網格點個數達5033萬(2048×384×64)。各套網格均在壁面處進行了加密。

圖4 計算得到的密度梯度圖Fig.4 Density gradient magnitude of the computation

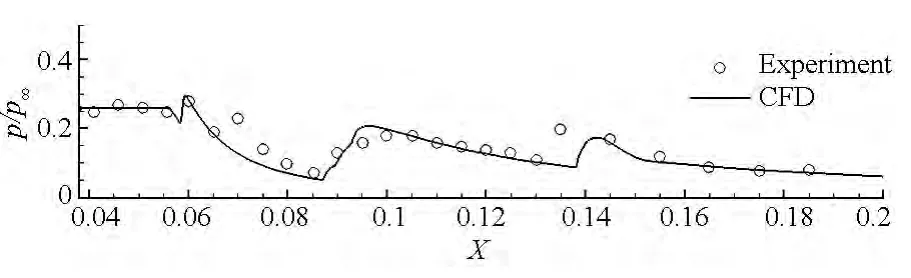
圖5 下表面壓力分布Fig.5 Lower surface pressure distribution

圖4給出了最密網格下湍流模型計算所得到的流場對稱面密度梯度云圖，可以發現數值計算結果清晰地捕獲了進氣道內復雜的波系結構。圖5給出了進氣道下壁面無量綱壓力分布計算與實驗結果的對比。從圖中結果可以看出湍流模型的計算值與實驗值在整體分布規律上都比較符合，這表明本文所發展的GPU求解器對可壓縮湍流定常問題的模擬是可行的。

圖6給出了不同網格下單塊GPU與單個CPU核心的計算時間對比及相應的加速比。圖中所示的時間為每迭代步所消耗的平均時間，可以看出GPU計算具有明顯的速度優勢，相對于單個CPU核心而言，隨著網格量的增加，GPU的加速比由最初的107倍逐漸增大至125倍。由加速比曲線可發現，小網格量下的加速比明顯低于大網格量的情況，即GPU非常適合處理大網格量的計算任務。同時，隨著網格量的增加，加速比趨于平緩，這是由于GPU中用于并行計算的CUDA核心數及可并發執行的線程塊數是有限的，當CUDA核心的利用率達到飽和時一些線程將會采用串行方式執行，此時加速比將不再增加而趨于穩定。對于不同架構的設備，這個飽和值是不同的，可以看出，當前使用的GPU負載飽和值為500萬以上的網格量。

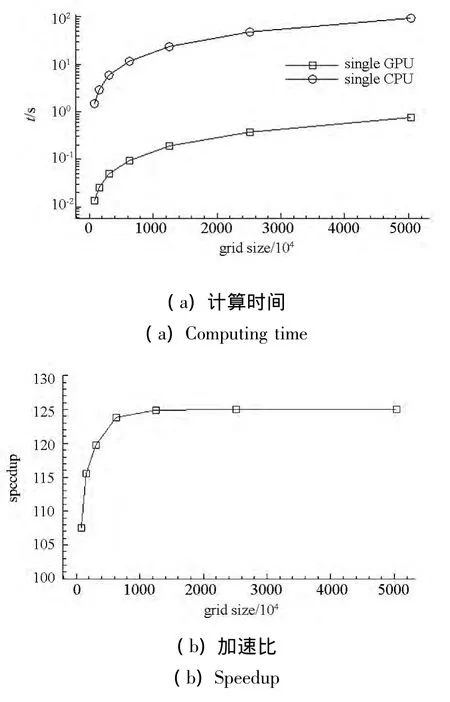
圖6 不同網格的計算時間與加速比Fig.6 Computing time and speedup for different grid sizes

并行效率是并行計算必須關注的性能指標。受顯存容量的限制，單塊GPU所能處理的最大網格量是有限的(對于定常湍流問題，6GB顯存至多可處理5000萬網格)，考慮到網格規模大小對GPU的性能發揮影響較大，為了真實反映同步與通信開銷對并行效率的影響，本文定義并行效率如下:對于某個計算任務，假設它在多塊GPU上并行處理的時間為tp，而對每個GPU來說都負載一定數量的網格(單個或多個分區)，設所有GPU單獨處理相應的負載所需時間的平均值為ts，則并行效率為ts與tp之比。上述的GPU單獨處理既不考慮節點間通信又不考慮節點內通信。對于本算例，每塊GPU的負載網格量都相等，且網格拓撲結構簡單無節點內通信。表1給出了4塊GPU在不同網格量下的計算時間與并行效率，可以看出，較小網格量下GPU的并行效率不高，隨著網格量的增加GPU的并行效率逐漸提高。這是因為隨著網格量的增加，節點間的通信時間在總的時間中所占比重逐漸減小所以并行效率得到提高。由表中數據可知，應用本文所發展的計算與通信的重疊算法，可使并行效率得到較大提高，相對于無重疊的并行計算，四套網格下內點通量計算與數據傳輸及通信的重疊可使并行效率提高10%以上。

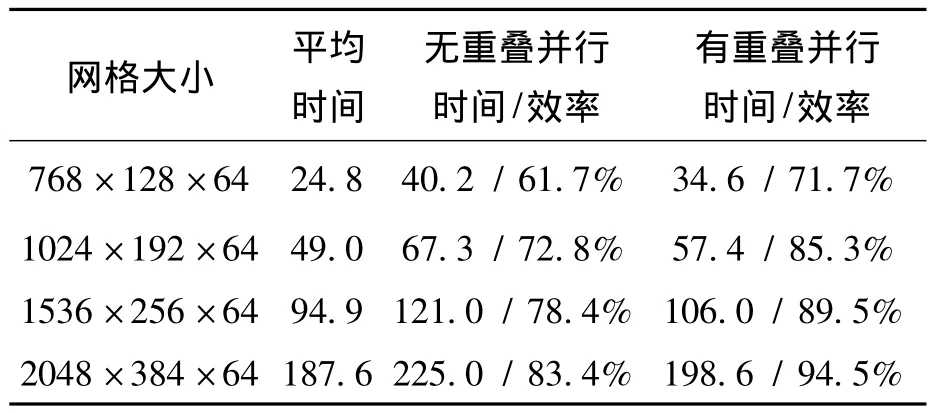
表1 計算時間與并行效率Tab.1 Computing time and parallel efficiency

3.2 超聲速進氣道

針對文獻［12］所述的空天飛機模型，本文計算了馬赫數為4.94，攻角為－5°的實驗狀態，對應的雷諾數為5.26×107m。空天飛機的長度為0.29m，文獻提供了高精度的實驗結果。計算方法如前所述，按定常湍流狀態考慮，壁面采用絕熱條件假設。

圖7所示為空天飛機的表面及對稱面網格分布，網格總量為1.34億，共有26個分區，壁面第一層網格高度為1×10－6m。采用4塊GPU并行計算，每塊GPU負載網格量為3350萬左右。圖8給出空天飛機的壓力及流線分布，因外形復雜，流場中不可避免地會出現激波與激波干擾及流動分離等現象。

圖7 空天飛機計算網格Fig.7 Computational grid for the space shuttle

圖9給出了機身對稱面中心線上表面的壓力分布，可以看出，計算結果與實驗結果吻合較好，能夠反映壓力的變化趨勢，這說明了求解器對復雜外形模擬具有很好的適應性。

4塊GPU并行計算時，每迭代步所消耗的時間為0.667秒，每塊GPU單獨處理的平均時間為0.611秒，計算得到的并行效率為91.6%，與超聲速進氣道算例的最高并行效率相比有所降低。這主要是因為單塊GPU負載的網格分區過多(尾流場包含18個分區，分配在兩個GPU上)引起同步時間消耗增多。此外，負載不平衡也造成了一定的影響，雖然4個GPU所負載的網格量基本相等，但是內部邊界及物理邊界條件(如壁面條件、遠場條件等)更新個數并不相等，分區過多導致了節點內的邊界更新操作過多從而影響了整體并行效率。

圖8 空天飛機壓力云圖及空間流線分布Fig.8 Pressure contours and stream lines distribution of the space shuttle

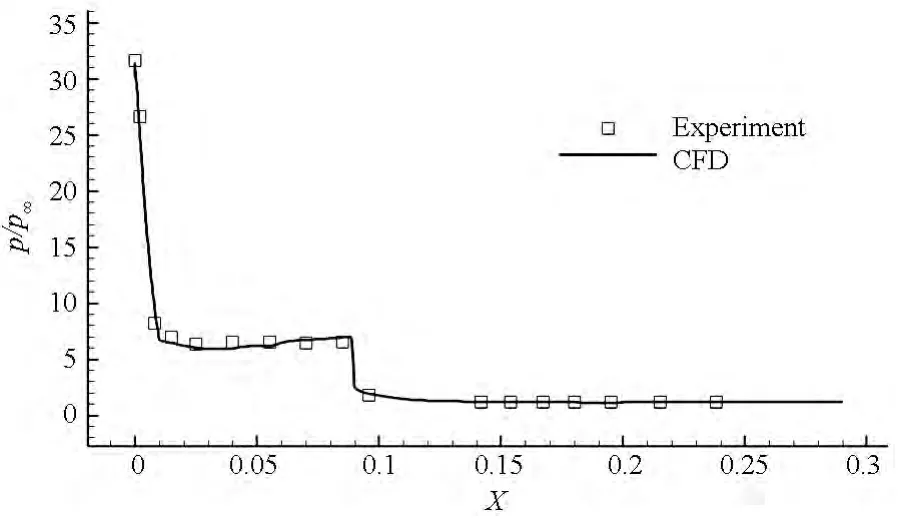
圖9 空天飛機對稱面上表面的壁面壓力分布Fig.9 Pressure coefficient distribution along the upper surface in the symmetry plane

4 結論

本文建立的基于GPU的可壓縮湍流求解器，可以快速準確地對超聲速流動中的湍流問題進行求解。為了達到良好的加速效果，根據最新的GPU架構特點對GPU程序的算法結構進行了調整與優化，采用兩個超聲速流動算例驗證了GPU求解器的準確性與適應性，實現了多GPU上復雜外形上億量級網格的快速計算，在最新的GTX TITAN Black GPU上取得了可觀的加速比與并行效率。根據研究結果，得出以下結論:

1)不同架構的GPU對應不同的優化算法，對于重復數據的讀取，在計算能力3.5的設備上，使用共享內存或寄存器移位等優化加速技術并不能取得明顯的加速效果。

2)利用Hyper－Q特性，可以實現GPU計算與PCIe數據傳輸、MPI通信的高度重疊，能有效掩蓋邊界交換所帶來的時間延遲。

3)從GPU的性能發揮及并行效率方面考慮，GPU負載的網格量應越大越好。對于本文使用的GTX TITAN Black GPU，最佳的負載網格量應在500萬以上。

References)

［1］NVIDIA Corporation.NVIDIA CUDA C Programming Guide Version6.5［EB/OL］.［2014－08－01］.http://docs.nvidia.com/cuda/pdf/CUDA-C-Programming-Guide.pdf.

［2］Shinn A F.Large eddy simulations of turbulent flows on graphics processing units:application to film cooling flows［D］.USA:University of Illinois at Urbana Champaign，2011.

［3］Cao W，Xu C F，Wang Z H，et al.CPU/GPU computing for a multi-block structured grid based high-order flow solver on a large heterogeneous system［J］.CLUSTER COMPUT，2014，17(2):255－270.

［4］Fu L，Gao Z H，Xu K，et al.A multi-block viscous flow solver based on GPU parallel methodology［J］.Computers＆Fluids，2014，95:19－39.

［5］Khajeh-Saeed A，Perot J B.Direct numerical simulation of turbulence using GPU accelerated supercomputers［J］.Journal of Computational Physics，2013，235:241－257.

［6］Menter F R.Influence of freestream values on k－ω turbulence model prediction［J］.AIAA Journal，1993，30(6):1657－1659.

［7］Kim K H，Kim C，Rho O H.Methods for the accurate computations of hypersonic flows I.AUSMPW+scheme［J］.Journal of Computational Physics，2001，174(1):38－80.

［8］The Portland Group.CUDA Fortran Programming Guide and Reference Release 2013，version 13.10［EB/OL］.［2013］.http://www.pgroup.com/resources/docs.htm.

［9］Ruetsch G，Fatica M.CUDA fortran for scientists and engineers:best practices for efficient CUDA fortran programming［M］.Holland:Elsevier，2013.

［10］Salvadore F，Bernardini M，Botti M.GPU accelerated flow solver for direct numerical simulation of turbulent flows［J］.Journal of Computational Physics，2013，235:129－142.

［11］Reinartz B U，Herrmann C D，Ballmann J，et al.Aerodynamic performance analysis of a hypersonic inlet isolator using computation and experiment［J］.Journal of Propulsion and Power，2003，19(5):868－875.

［12］李素循.典型外形高超聲速流動特性［M］.北京:國防工業出版社，2007.LI Suxun.Hypersonic flow characteristics around typical con Figuration［M］.Beijing:National Defense Industry Press，2007.(in Chinese)