部分頻帶干擾下偽碼跟蹤誤差分析*

瞿 智，楊 俊，楊建偉

(國防科技大學機電工程與自動化學院，湖南長沙410073)

擴頻測距系統中，精確的偽碼同步是高精度測控和精密測量定軌的核心。部分頻帶干擾作為一種常見的干擾，可能會嚴重惡化偽碼跟蹤精度［1-2］。干擾環境中的偽碼跟蹤性能分析，是擴頻測距系統設計的重要內容［2-4］。

傳統方法分析部分頻帶干擾下的偽碼跟蹤性能時，假設干擾帶寬比較寬，忽略了偽碼的非理想隨機特性:文獻［5］結合跟蹤環路的穩態特性分析了寬帶白噪聲條件下的偽碼跟蹤誤差;文獻［6-9］基于偽碼功率譜給出了帶限高斯白噪聲條件下偽碼跟蹤誤差的解析表達式。這些文獻并未給出干擾帶寬的定量要求，沒有明確這些分析方法的適用條件。同時，一部分文獻在分析單頻干擾下的偽碼跟蹤性能時，考慮了偽碼的非理想隨機特性:文獻［10］引入導航信號模型分析了單頻干擾導致的偽碼跟蹤誤差;文獻［11-12］基于周期偽碼的離散譜分析了單頻干擾對延遲鎖定環鑒相曲線的影響，并定義了干擾誤差包絡(Interference Error Envelope，IEE)和干擾平滑誤差(Interference Running Average，IRA)兩個參量來評估干擾對導航接收機測距性能的影響;文獻［13-14］基于偽碼的離散譜推導了單頻干擾下偽碼跟蹤的最大誤差和平均誤差。

可以看出，在部分頻帶干擾下缺乏有效的分析來衡量不同干擾帶寬情況下偽碼跟蹤性能的分析精度。忽略偽碼非理想隨機特性，基于偽碼簡化譜分析，計算成本小，但可能存在較大的分析誤差。考慮非理想隨機特性，基于偽碼精細譜分析，分析精度高，但計算成本高。

1 系統與信號模型

1.1 偽碼跟蹤系統模型

擴頻測距接收機的測距精度主要由碼環的跟蹤性能決定，偽碼跟蹤的基本結構如圖1所示。接收機模擬通道假定為理想的帶通濾波器，并考慮信號載頻已剝離，那么接收機前端濾波器等效為帶內幅度增益為1和截止頻率為B/2的低通濾波器hr(t)。假定擴頻信號的頻率和相位能夠精確跟蹤，主要研究碼環的跟蹤性能。

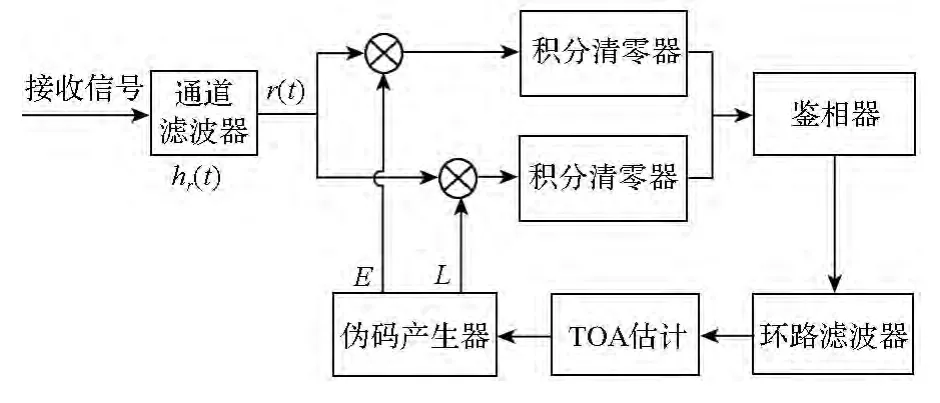
圖1 基帶信號的偽碼跟蹤處理流程Fig.1 Code tracking process of baseband signal

不考慮熱噪聲，基帶接收信號的模型為

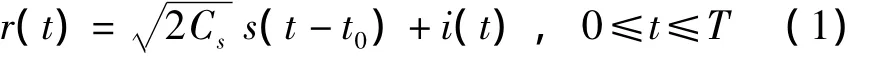
式中，Cs表示接收的有用信號功率，s(t)表示經過理想低通濾波器的基帶擴頻信號，i(t)表示部分頻帶干擾，t0表示相對于起點的時間延遲，T表示積分時間。

1.2 部分頻帶干擾信號模型

假定干擾是高斯的，功率譜是帶限且帶內平坦的，即

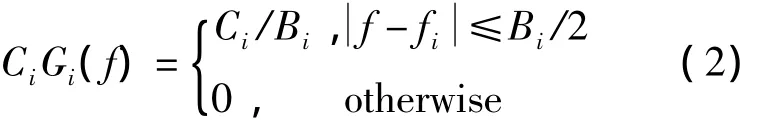
式中，Ci表示接收的干擾信號功率，Gi(f)表示干擾歸一化功率譜，fi表示干擾中心頻率，Bi表示干擾帶寬。

1.3 擴頻信號模型

目前，分析部分頻帶干擾下的偽碼跟蹤性能時，假定干擾帶寬足夠大，并忽略擴頻碼的非理想隨機特性［7］。對于二進制相移鍵控(Binary Phase Shift Keying，BPSK)調制，擴頻信號的歸一化功率譜模型簡化為

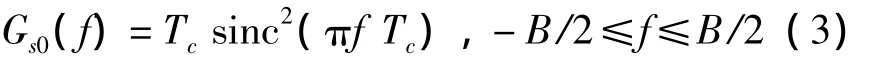
式中，Tc表示碼片周期。這里假定偽碼為理想隨機碼，僅關注了脈沖調制賦形，并沒有體現擴頻信號的偽隨機特性。因此這個簡化的平滑譜不能用來研究具體偽碼跟蹤性能的細節特征。

由于偽碼并非理想的隨機信號，并且短周期碼廣泛應用到全球導航衛星系統(Global Navigation Satellite System，GNSS)和遙測、跟蹤和指揮(Telemetry，Track and Command，TT＆C)中的精密測距和定位，基于簡化的平滑譜模型的分析不能滿足高精度測距應用的需求。充分考慮短周期偽碼的非理想隨機特性和短周期特性，引入擴頻信號模型

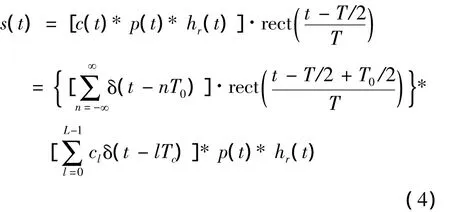
式中，*表示卷積，c(t)表示偽碼序列，p(t)表示脈沖編碼賦形，L表示偽碼序列長度，T0表示偽碼周期，且T=KT0，K∈Z+。

利用傅里葉變換，由式(4)可以得到擴頻信號頻譜為

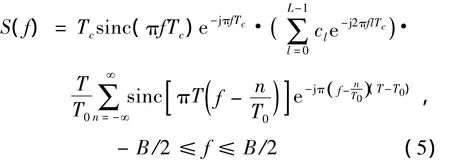
由于擴頻解擴的積分時間一般較長，擴頻信號精確的功率譜為

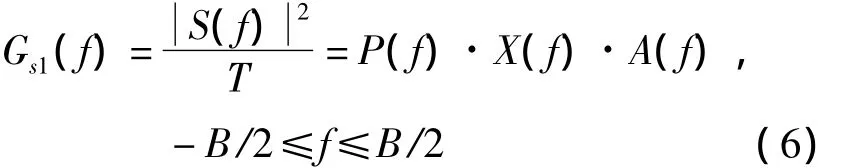
其中:

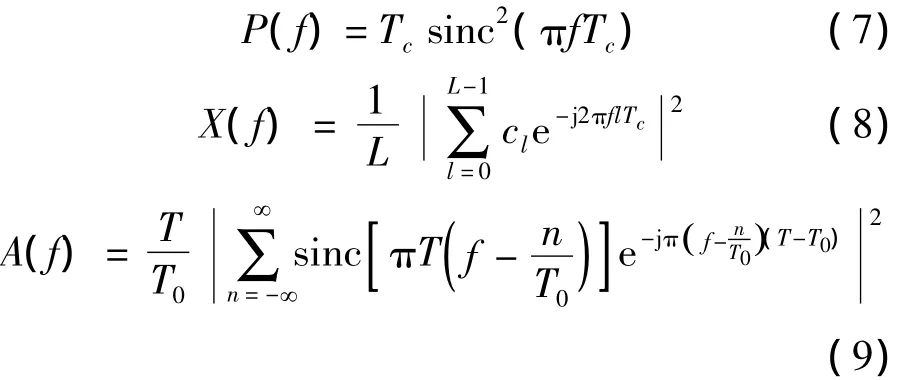
可以看出周期偽碼信號的功率譜由三部分組成，第一部分P(f)說明功率譜的基本形狀由脈沖編碼賦形決定，第二部分X(f)體現了偽碼的非理想隨機特性對功率譜的影響，第三部分A(f)反映了積分時間對功率譜細節特征的影響。

對于理想隨機碼，X(f)=1，并且取T=T0時，式(6)等價于式(3)。對于短周期碼，X(f)存在很大的幅度波動，這里以GPS L1 C/A碼為例，由式(8)得到PRN1～PRN32的功率譜最大波動量，見圖2。

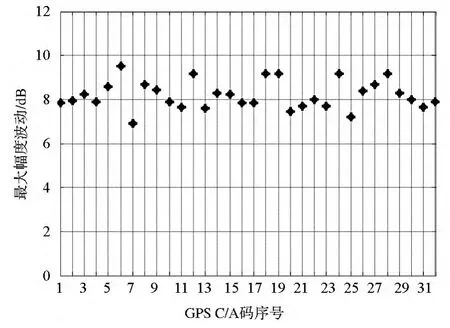
圖2 GPS L1 C/A碼功率譜最大波動量Fig.2 Maximum fluctuation of power spectrum of GPS L1 C/A codes

可以看出，偽碼非理想隨機特性導致的功率譜波動量達到6.91～9.53dB，這可能導致較大的偽碼跟蹤誤差變化。尤其在部分頻帶干擾帶寬較窄的情況下，擴頻信號功率譜局部頻段的幅度波動可能嚴重惡化偽碼跟蹤性能。下面基于精細功率譜，定量分析偽碼非理想隨機特性導致的偽碼跟蹤精度變化。

2 偽碼跟蹤誤差特性分析

2.1 偽碼跟蹤誤差

當接收機碼環采用相干鑒相時，部分頻帶干擾下偽碼跟蹤誤差的方差為［8］

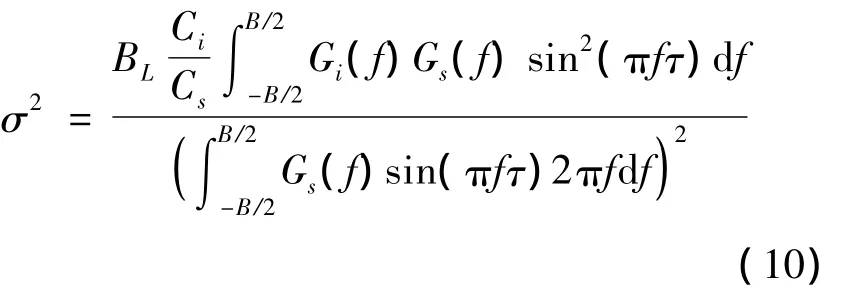
式中，BL表示碼環等效噪聲帶寬，τ表示碼環超前滯后間隔。

將式(2)代入式(10)，可得

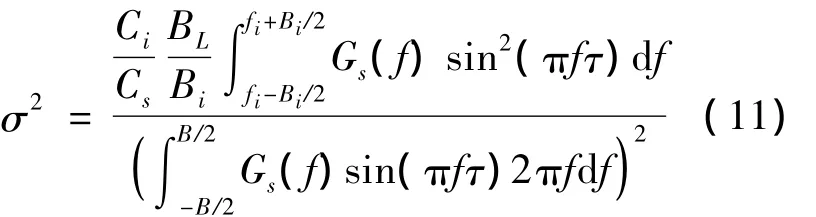
式(11)表明偽碼譜特性很大程度上影響著部分頻帶干擾下的偽碼跟蹤誤差，并且隨著干擾中心頻率和干擾帶寬的變化，跟蹤誤差的變化也與偽碼功率譜密切相關。偽碼非理想隨機特性導致的功率譜波動，將引起偽碼跟蹤誤差的變化。尤其在干擾帶寬較窄時，從式(11)的分子部分可以看出，跟蹤性能對偽碼功率譜局部頻段的特征將更加敏感。

2.2 相對誤差系數

為定量分析偽碼非理想隨機特性對跟蹤精度的影響，這里引入相對誤差系數

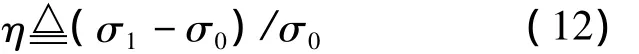
式中，σ0表示基于簡化的擴頻信號功率譜Gs0(f)得到的跟蹤誤差，σ1表示基于精細的擴頻信號功率譜Gs1(f)得到的跟蹤誤差。

相對誤差系數反映了偽碼非理想隨機特性導致的功率譜波動對跟蹤誤差的影響，也可以看作部分頻帶干擾下準確的跟蹤誤差相對于基于簡化譜分析得到的跟蹤誤差的相對誤差，以此來衡量簡化譜分析的適用性。

由于在寬帶范圍內積分，偽碼功率譜波動對積分結果的影響可忽略［2］，那么由式(11)和式(12)可以得到

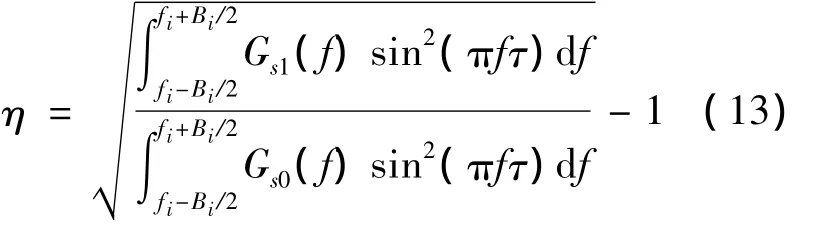
從式(13)可以看出，相對誤差系數不再與干信比和環路等效噪聲帶寬等參量有關。同時，碼環超前滯后間隔τ較小(一般情況下僅0.001～1個Tc)，其對相對誤差系數的影響非常小。總體來看，相對誤差系數主要受偽碼譜特性和干擾特征參量的影響。

這里首先針對兩種典型情況予以說明。

當干擾帶寬極窄時，即Bi〈1/(5T)時，式(13)可以化簡為

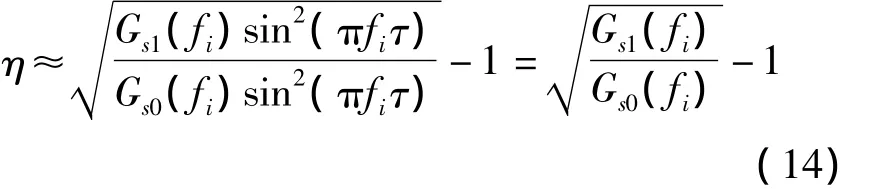
根據式(3)、式(6)和式(14)，可以得到

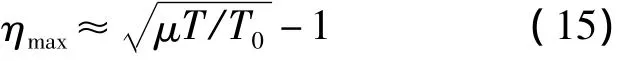
式中，μ表示偽碼功率譜最大波動量。

由式(15)可以看出，在干擾帶寬較窄時，偽碼功率譜波動越大或積分時間越長，基于兩種譜的誤差分析差異越大，反映出基于簡化譜的分析也越不準確。以GPS L1 C/A PRN 5碼為例，即使在T=T0時，相對誤差系數也高達1.68。也就是說，此時的偽碼跟蹤誤差是基于簡化譜分析結果的2.68倍，這說明基于簡化的平滑譜分析已完全不可用。

另一種情況，是Bi〉5/T0，這在工程實踐中比較常見。隨著干擾帶寬的增加，相對誤差系數將越來越小直至接近于0，這說明基于簡化的平滑譜的跟蹤誤差分析將逐漸適用。這里需要給出明確的界限以便于實際應用中能夠確定適用簡化譜的條件。由于偽隨機碼的多樣性，下面將以GPS L1 C/A碼為例進行數值分析，給出各自的簡化譜適用條件，并通過統計分析給出簡化譜適用的經驗條件。

3 數值分析

干擾帶寬是影響基于兩種譜分析的性能差異的主要特征參量，這里基于不同的干擾帶寬對比兩種跟蹤精度分析。數值分析參數見表1。

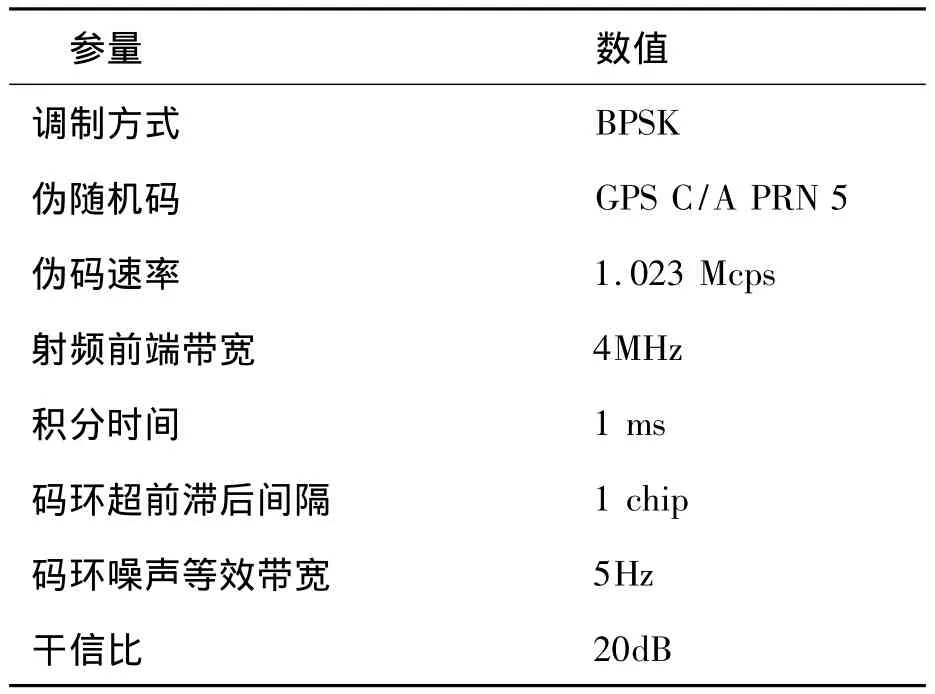
表1 數值分析參數表Tab.1 Parameters of numerical analysis

當干擾帶寬為100Hz時，基于兩個譜分析的偽碼跟蹤誤差和相對誤差系數分別見圖3和圖4。可以看出，當干擾帶寬較小時，兩者的差異明顯，相對誤差系數可達1.681。這說明偽碼的非理想隨機特性在較窄的部分頻帶干擾中對跟蹤精度的影響較大，不能忽略，此時基于簡化譜的偽碼跟蹤精度分析已不可用。

當干擾帶寬為300kHz時，基于兩個譜分析的偽碼跟蹤誤差和相對誤差系數分別見圖5和圖6。兩個跟蹤誤差趨于一致，相對誤差系數小于0.06。這說明在干擾帶寬較寬時，偽碼的非理想隨機特性對碼跟蹤誤差的影響很小，跟蹤精度的分析可完全采用簡化的平滑譜以減少計算量。

由前面的分析可知，分別基于簡化的功率譜和精細的功率譜得到偽碼跟蹤誤差的差異隨著干擾帶寬的增加而減小。只有這個差異小于一定的條件時，基于簡化譜的分析才是適用的。為此，設定當相對誤差系數小于0.2時，即偽碼非理想隨機特性引起的跟蹤誤差波動小于20%時，可以認為基于簡化譜的分析是適用的。

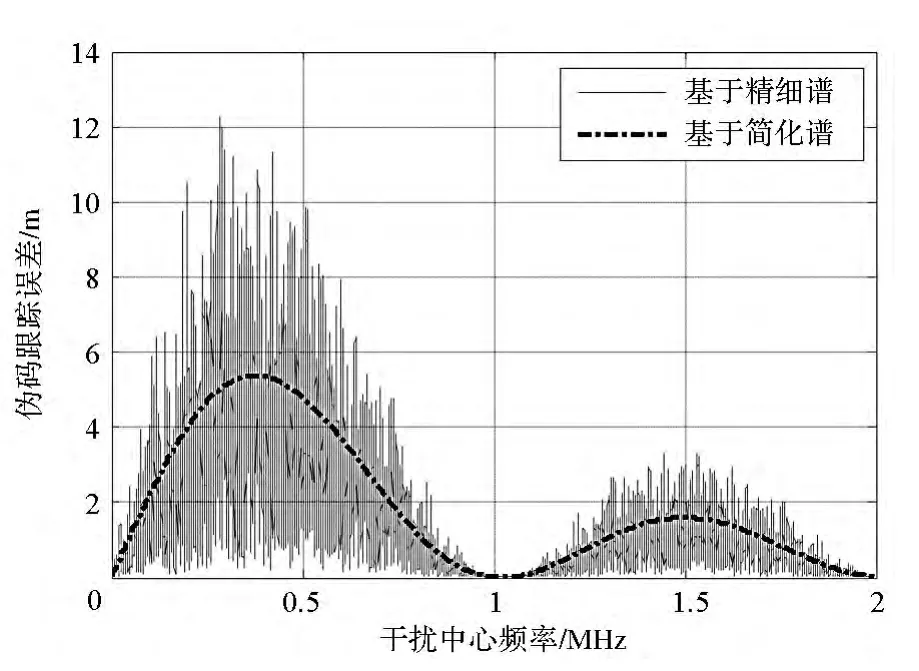
圖3 基于兩種譜的跟蹤誤差對比(Bi=100Hz)Fig.3 Comparison of tracking error based on two spectrums(Bi=100Hz)

圖4 相對誤差系數(Bi=100Hz)Fig.4 Relative error coefficient(Bi=100Hz)

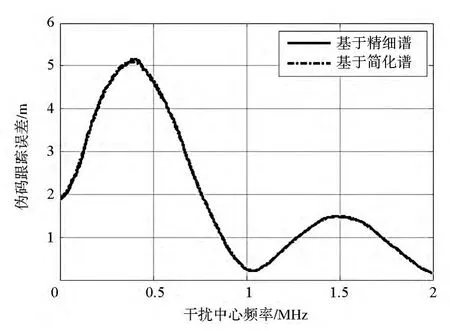
圖5 基于兩種譜的跟蹤誤差對比(Bi=300kHz)Fig.5 Comparison of tracking error based on two spectrums(Bi=300kHz)

不同干擾帶寬條件下，GPS L1 C/A PRN 5最大的相對誤差系數見圖7。隨著干擾帶寬的增加，最大相對誤差系數逐漸減小，基于簡化譜的分析也更加準確。可以看出，當干擾帶寬大于約200kHz時，基于簡化譜的分析誤差小于20%。

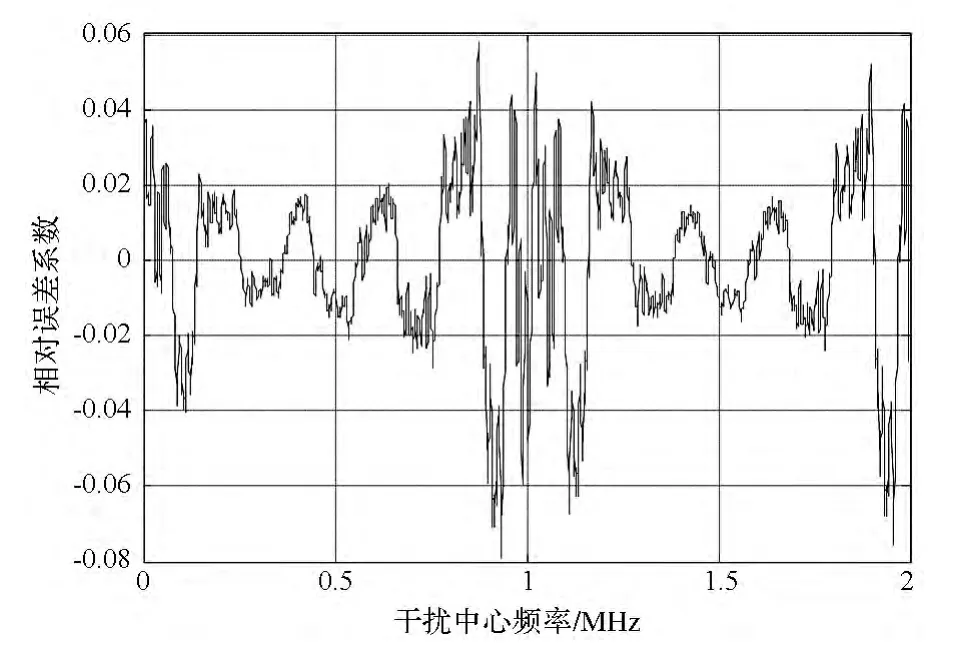
圖6 相對誤差系數(Bi=300kHz)Fig.6 Relative error coefficient(Bi=300kHz)

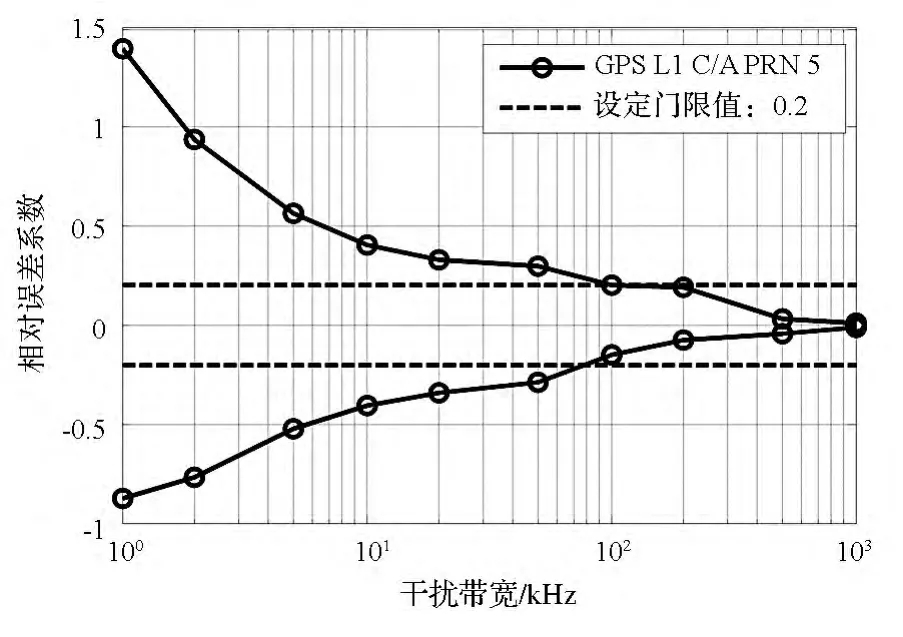
圖7 最大相對誤差隨干擾帶寬的變化特性(GPS C/A PRN 5)Fig.7 Maximum relative error versus interference bandwidth(GPS C/A PRN 5)

基于簡化譜的分析誤差主要是由偽碼的非理想隨機特性引起的，但不同偽碼的非理想隨機特性存在一定的差異。這里給出GPS L1的32個C/A碼在基于簡化譜的分析誤差不超過20%時的最小干擾帶寬，見表2。

從表中可以看出，PRN 17的非理想隨機特性對誤差分析的影響最大，干擾帶寬大于285kHz時，才能基于簡化譜進行誤差分析，而PRN 32的非理想隨機特性對誤差分析的影響相對較小，只要干擾帶寬大于26kHz，基于簡化譜的分析誤差就小于20%。總體來看，對于大多數碼，干擾帶寬大于100kHz(即偽碼周期的頻率的100倍)時，相對誤差系數小于20%。基于保守分析，對于所有偽碼，干擾帶寬大于300kHz(300/T0)時，基于簡化譜的分析誤差可忽略，這可以作為適用基于簡化譜分析的一般條件。同時，可以將此帶寬作為劃分窄帶干擾和寬帶干擾的分界線。當基于簡化譜的分析誤差小于20%時，偽碼非理想隨機特性可忽略，認為干擾為寬帶干擾;當基于簡化的分析誤差大于20%時，偽碼非理想隨機特性對碼跟蹤精度的影響不可忽略，此時干擾為窄帶干擾。

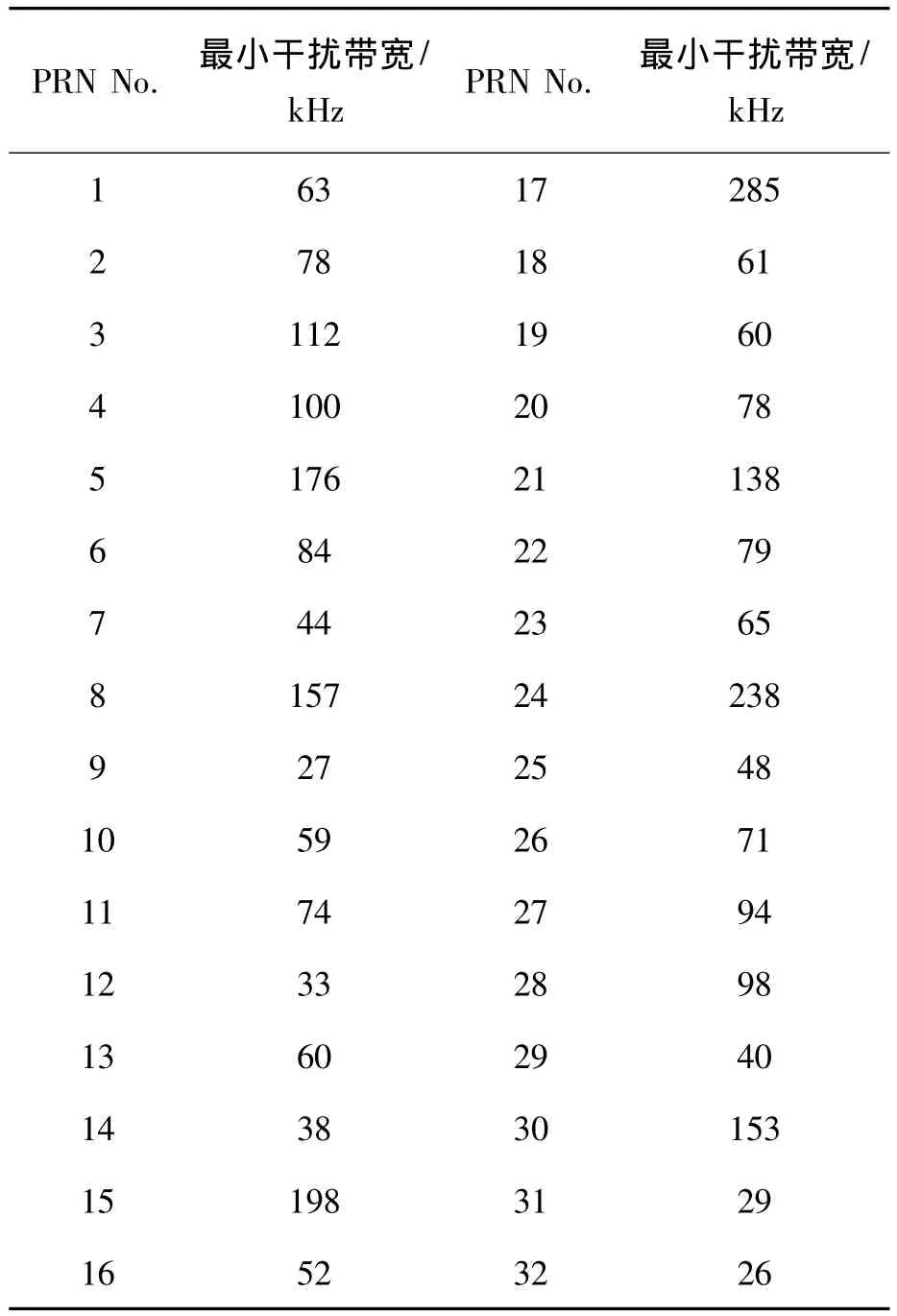
表2 最小干擾帶寬(GPS C/A碼)Tab.2 Minimum interference bandwidth(GPS C/A codes)

4 結論

本文定量分析了偽碼非理想隨機特性對部分頻帶干擾下的偽碼跟蹤精度的影響。引入能夠描述偽碼非理想隨機特性的精確功率譜模型，分析了偽碼跟蹤誤差，并以傳統的基于簡化的平滑譜模型得到的偽碼跟蹤誤差為基準進行了對比分析。當干擾帶寬較寬時，偽碼非理想隨機特性對跟蹤誤差的影響較小，但當干擾帶寬較小時，基于平滑譜模型得到的偽碼跟蹤性能的分析誤差較大。本文定義了相對誤差系數，能夠定量描述由偽碼非理想隨機特性導致理論分析的相對誤差。給出了GPS L1 C/A碼在相對誤差小于20%時的最小干擾帶寬，并將這個帶寬作為簡化譜適用的條件門限。分析發現，最小干擾帶寬不超過偽碼周期的頻率的300倍。當干擾帶寬大于這個帶寬時，偽碼非理想隨機特性在偽碼跟蹤精度分析中可忽略，反之，則需要考慮非理想隨機特性導致的擴頻信號功率譜波動，只有基于精細的偽碼譜模型才能得到精確的偽碼跟蹤誤差分析。

References)

［1］Daher J K，Harris J M，Wheeler M L.An evaluation of the radio frequency susceptibility of commercial GPS receivers［J］.IEEE Aerospace and Electronic Systems Magazine，1994，9(10):21-25.

［2］Kaplan E D，Hegarty C.Understanding GPS:principles and applications［M］.2nd ed.USA:Artech House，2006.

［3］Misra P，Enge P.Global positioning systems:signal measurements and performance［M］.2nd ed.USA:Ganga-Jamuna Press，2010.

［4］謝鋼.GPS原理與接收機設計［M］.北京:電子工業出版社，2012.XIE Gang.Principles of GPS and receiver design［M］.Beijing:Publishing House of Electronics Industry，2012.(in Chinese)

［5］Van Dierendonck A J，Fenton P，Ford T.Theory and performance of narrow correlator spacing in a GPS receiver［J］.Navigation，1992，39(3):265-283.

［6］Betz J W.Effect of narrowband interference on GPS code tracking accuracy［C］//Proceedings of the National Technical Meeting of the Institute of Navigation，2000:16-27.

［7］Betz J W.Effect of partial-band interference on receiver estimation of C/N0:theory［C］//Proceedings of the National Technical Meeting of the Institute of Navigation，2001:817-828.

［8］Betz J W，Kolodziejski K R.Generalized theory of code tracking with an early-late discriminator part I:lower bound and coherent processing［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45(4):1538-1550.

［9］Betz J W，Kolodziejski K R.Generalized theory of code tracking with an early-late discriminator part II:noncoherent processing and numerical results［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45(4):1551-1564.

［10］Jang J，Paonni M，Eissfeller B.CW Interference effects on tracking performance of GNSS receivers［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48(1):243-258.

［11］Motella B，Savasta S，Margaria D，et al.An interference impact assessment model for GNSS signals［C］//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation，2008:900-908.

［12］Motella B，Savasta S，Margaria D，et al.Method for assessing the interference impact on GNSS receivers［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47(2):1416-1432.

［13］Liu Y Q，Ran Y H，Ke T，et al.Code tracking performance analysis of GNSS signal in the presence of CW interference［J］.Signal Processing，2011，91(4):970-987.

［14］Liu Y Q，Ran Y H，Ke T，et al.Characterization of code tracking error of coherent DLL under CW interference［J］.Wireless Personal Communications，2012，66(2):397-417.