基于結構方程模型的東北地區主要旱田土壤有機碳平衡關系研究

李 慧，汪景寬，裴久渤，李雙異

沈陽農業大學土地與環境學院, 沈陽 110866

基于結構方程模型的東北地區主要旱田土壤有機碳平衡關系研究

李 慧，汪景寬*，裴久渤，李雙異

沈陽農業大學土地與環境學院, 沈陽 110866

土壤有機碳平衡是一個復雜的過程，是潛變量與潛變量，潛變量與可測變量及可測變量之間相互作用的結果。結構方程模型的建立很好地描述了這一復雜關系。應用2011年東北地區敦化、榆樹、公主嶺、昌圖和阜新5個典型縣(市)農田表層土壤有機碳(0—20 cm)數據，建立了東北地區主要旱田土壤有機碳平衡關系結構方程模型，探討了影響有機碳平衡關系的各潛變量和可測變量的相互影響關系。結果表明：在土壤有機碳的平衡過程中，潛變量之間(氣候環境、土壤性質和人為管理)具有兩兩相關性，土壤性質對有機碳平衡具有直接正向作用，其路徑系數為1.01；氣候環境和人為管理通過土壤性質傳遞并影響土壤有機碳平衡，且氣候環境的影響力大于人為管理的影響力，其路徑系數分別為1和0.87。因此，針對有機碳平衡關系計算出的路徑系數, 需要強化人為管理在土壤有機碳平衡過程中的作用, 特別要在耕作方式上加強管理, 促使有機碳平衡向更優化方向發展。

潛變量；路徑系數；影響因素；耕作方式

陸地生態系統碳循環研究對于應對全球氣候變暖具有重要意義，土壤碳固定是減緩溫室氣體排放的主要途徑之一[1- 2]。土壤有機碳的平衡是一個復雜的過程，不僅受氣候、植被、土壤屬性、地形等自然因素影響，也受土地利用變化、耕種管理措施等人為因素的影響，且各種因素之間也存在相互作用。多種影響因子共同決定著土壤有機碳在空間上的分布和再分布格局，以及土壤有機碳的形成、分解的轉化方向和變化速率[3- 8]。

在土壤有機碳平衡關系研究中，人們多從定性的角度來分析影響有機碳的平衡因素，即使進行定量化研究也僅僅采用回歸分析、因子分析、相關性分析、多變量方差分析等[9]傳統的方法來闡述各要素之間的關系。但是，這些方法僅限于可測變量的自變量與因變量之間的關系分析，事實上，可測變量不能完全描述有機碳平衡之間的內在關系，更需要弄清潛變量之間的關系，因為潛變量及其關系往往決定了有機碳平衡發展的方向[10]。結構方程模型(Structural Equation Modeling，SEM)解決了這一問題，該模型思想起源于20世紀20年代Sewall提出的路徑分析概念[11- 12]，Judea正式將其定義為結構方程模型[13]。目前該模型已在心理學、行為科學、教育學得到很大程度的應用，取得了較好的效果[14- 16]。在農業方面，王繼軍等初步將結構方程模型在農業生態經濟系統中進行了應用[10]；在土壤有機碳的研究中，Brahim等應用了結構方程模型對半干旱的地中海地區的土壤有機碳和土壤理化性質進行了研究[17]。

我國東北地區是主要的糧食生產基地，旱田占農田總面積的86.49%[18]，弄清東北地區旱田土壤有機碳平衡關系對于提高土壤有機碳固碳潛力和指導農業生產具有重要的現實意義。基于此，本研究應用東北地區典型糧食生產基地(敦化市、榆樹市、公主嶺市、昌圖縣和阜新縣5個典型市縣)的99個采樣點數據，運用結構方程模型探討了東北地區主要旱田土壤有機碳平衡關系，以期為東北地區旱田土壤有機碳的循環和固定研究提供參考和依據。

1 材料與方法

1.1 研究區概況

東北地區主要包括遼寧省、吉林省和黑龍江省。本研究選取遼寧省阜新縣和昌圖縣，吉林省公主嶺市、敦化市和榆樹市作為研究區域(圖1)。其中，阜新縣位于遼寧西部，地理位置為121°1′—122°46′E，41°41′—42°56′N，耕地面積約占轄區面積35%，土壤類型以褐土為主；昌圖縣位于遼寧省最北部，松遼平原南端，遼、吉、蒙三省(區)交界，地理位置為123°32′—124°26′E，42°23′—43°29′N，耕地面積約占轄區面積65%，是我國東北重要商品糧基地縣，土壤類型以棕壤和黑土為主；公主嶺市地處吉林省中西部，松遼平原腹地，位于124°02′—125°18′E，43°11′—44°9′N，耕地面積約占所轄面積55%，是國家首批確定的商品糧基地之一，土壤類型以黑土為主；敦化市位于吉林省東部山區，長白山腹地，四周環山，地處127°28′—129°13′E，42°42′—44°30′，耕地面積約占轄區面積9%，土壤類型以灰棕壤為主；榆樹市地處吉林省中北部，地理位置為126°01′—127°05′E，44°30′—45°15′N，耕地面積約占轄區面積68%，該市坐落在世界黃金玉米帶上，是吉林省著名的產糧大市，也是全國重點商品糧基地，被譽為“天下第一糧倉”，主要土壤類型為黑鈣土。

圖1 研究區采樣點位置Fig.1 Location of sampling sites in study areas

1.2 數據來源

采樣點是土壤調查過程中最小的的基本單元，選擇采樣點數據進行分析更具可操作性。研究區共采集2011年表層土壤(0—20 cm)采樣點114個，根據覆蓋多種地貌類型、土壤類型的原則進行采樣，采樣時在中心樣點四周呈輻射狀另采4個樣點，用四分法對5個樣點混合樣進行選取，以減小采樣誤差。每個中心樣點均采用GPS進行定位，樣點間距約為0.5km，并詳細記錄了樣點的氣候，土壤性質、農戶管理等數據資料，通過整理和篩選，本研究共選取其中99個有效樣點進行模型的構建(圖1)。

1.3 研究方法

結構方程模型(SEM)是基于變量的協方差矩陣來分析變量之間關系的一種方法。目前最常用的是線性結構方程模型。結構方程模型有效地整合了統計學的因子分析與路徑分析兩大主流技術，主要用于對復雜的多變量研究數據進行處理。該方法是一種集因子分析和通徑分析于一身的可以描述不可直接測量變量之間關系的多元統計方法[19]，屬于驗證性模型。在結構方程模型中包含了兩種變量，一種是可以測量的顯變量，一種是不可直接測量的潛變量。結構方程模型由測量方程和結構方程兩部分構成，測量方程是用來描述潛變量和顯變量之間的關系，結構方程是用來描述潛變量與潛變量之間的關系。由下列方程表示：

x= ∧xξ+δ

(1)

y= ∧yη+ε

(2)

η=Bη+Γξ+ζ

(3)

其中,方程(1)和方程(2)被稱之為測量方程, 方程(3)則是結構方程。x是外生可測變量向量；ξ是外生潛變量向量；y是內生可測變量向量；η是內生潛變量向量；∧x為外生可測變量與外生潛變量之間的關系，是外生可測變量在外生潛變量上的因子負荷矩陣；∧y為內生可測變量與內生潛變量之間的關系，是內生可測變量在內生潛變量上的因子負荷矩陣；B是內生潛變量的關系陣；Γ則表示外生潛變量對于內生潛變量的影響；δ和ε為測量方程的誤差項；ζ為結構方程的誤差項。

1.4 軟件平臺

數據處理采用軟件Microsoft Excel和SPSS19.0。模型運行采用Amos 7.0。

2 東北地區主要旱田土壤有機碳平衡關系概念模型建立與計算

2.1 概念模型建立

根據東北地區土壤有機碳變化的特征，建立東北地區主要旱田土壤有機碳平衡關系的概念模型(圖2)，模型包括4個潛變量：自然環境ξ1、土壤性質ξ2、人為管理ξ3和土壤碳平衡η；10個可測變量：年均溫度x1、年均降水量x2、坡度x3、土壤質地x4、pHx5、肥料施用量x6、秸稈施用量x7、耕種方式x8、作物單產y1和土壤有機碳含量y2。

圖2 有機碳平衡關系概念模型(測量模型和結構模型)Fig.2 Conceptual model of organic carbon equilibrium(measurement model and structural model)

根據前人對于影響有機碳平衡關系及因素的分析，對于概念模型，給出如下假設：

假設1 自然環境對土壤有機碳平衡有正向的影響

假設2 土壤性質對土壤有機碳平衡有正向的影響

假設3 人為管理對土壤有機碳平衡有正向的影響

假設4 自然環境與土壤性質有相互影響

假設5 土壤性質與人為管理有相互影響

假設6 自然環境與人為管理有相互影響

2.2 結構方程計算

(1)結構方程模型數據處理及信度分析

表1 各變量一覽表及數據信度值Table 1 Variables list and data reliability values

應用SPSS19.0對99個采樣點數據進行分析處理，進行數據的有效度，即信度分析，信度分析結果如表1，4個潛變量的信度值分別為0.751、0.736、0.76、0.705，信度均大于0.7，認為數據具有較好的一致性。

(2)東北地區主要旱田土壤有機碳平衡關系的結構方程模型模擬

結構方程模型是一個驗證性模型，是一個擬合、評價、修正、再評價的反復過程，直至模型不僅具有統計學的理論意義，而更能從現實角度出發具有現實意義。

對已建立的概念模型和假設，利用Amos 7.0進行第一次初始模型擬合，擬合結果如圖3，模型擬合系數評價結果見表2。可以看出，人為管理對土壤有機碳平衡路徑系數/載荷系數是否顯著加以判定的P值為0.631，表明該路徑系數為零的概率達到了63.1%，大于5%的顯著性水平，沒有足夠理由認為其在95%置信水平下與零存在顯著性差異，顯著性檢驗沒有通過。模型擬合指數顯示模型擬合一般。依據建立模型的實際意義，需要對路徑系數進行釋放，采納修正指數的建議，對模型進行第二次擬合，通過模型的多次反復擬合、修正和運算，直至各路徑系數均通過顯著性檢驗(表3)，最終得出標準化系數修正模型(圖4)和潛變量及可測變量之間總的影響效果(表4)。

圖3 結構方程模型第一次擬合參數估計結果圖Fig.3 The first fitting results of parameter estimation

表2 第1次模型擬合系數估計結果Table 2 The first estimated results of modeling fitting coefficient

P表示假設檢驗中的概率; ***表示在P﹤0.05水平顯著

3 結果與分析

3.1 模型假設分析

在模型反復擬合、評價、修正過程后得到了如圖4的最后標準化系數修正模型，其結果表明初始模型假設中自然環境對有機碳平衡狀態有正向的影響以及人為管理對有機碳平衡狀態有正向的影響的兩個假設不被模型擬合的結果支持(表5)。

表3 第3次模型擬合系數估計結果Table 3 The third estimated results of modeling fitting coefficient

P表示假設檢驗中的概率; ***表示在P﹤0.05水平顯著

3.2 模型擬合指數分析

運用Amos7.0進行結構方程模型的分析，可以得到較多的擬合指數，根據許多學者對結構方程模型相關研究的建議，本研究采用絕對擬合指數、相對擬合指數和精簡指數三類擬合指數，包括x2/df、GFI、RMSEA、NFI、TLI、CFI、IFI、AIC和ECVI，并確定了擬合標準，分別為x2/df大于10表示模型很不理想，小于5可以接受，小于3則模型擬合較好；RMSEA介于0—1之間，小于0.05表示模型擬合較好，GFI、NFI、TLI、CFI、IFI應大于0.9，且越接近1越好，AIC和ECVI數值越小越好。本研究修正后模型擬合指數分析結果如表6所示。模型擬合指數總體表現較好，均達到擬合指數要求，認為從統計學角度經過修正后得到的東北地區主要旱田土壤有機碳平衡關系模型比較合理。

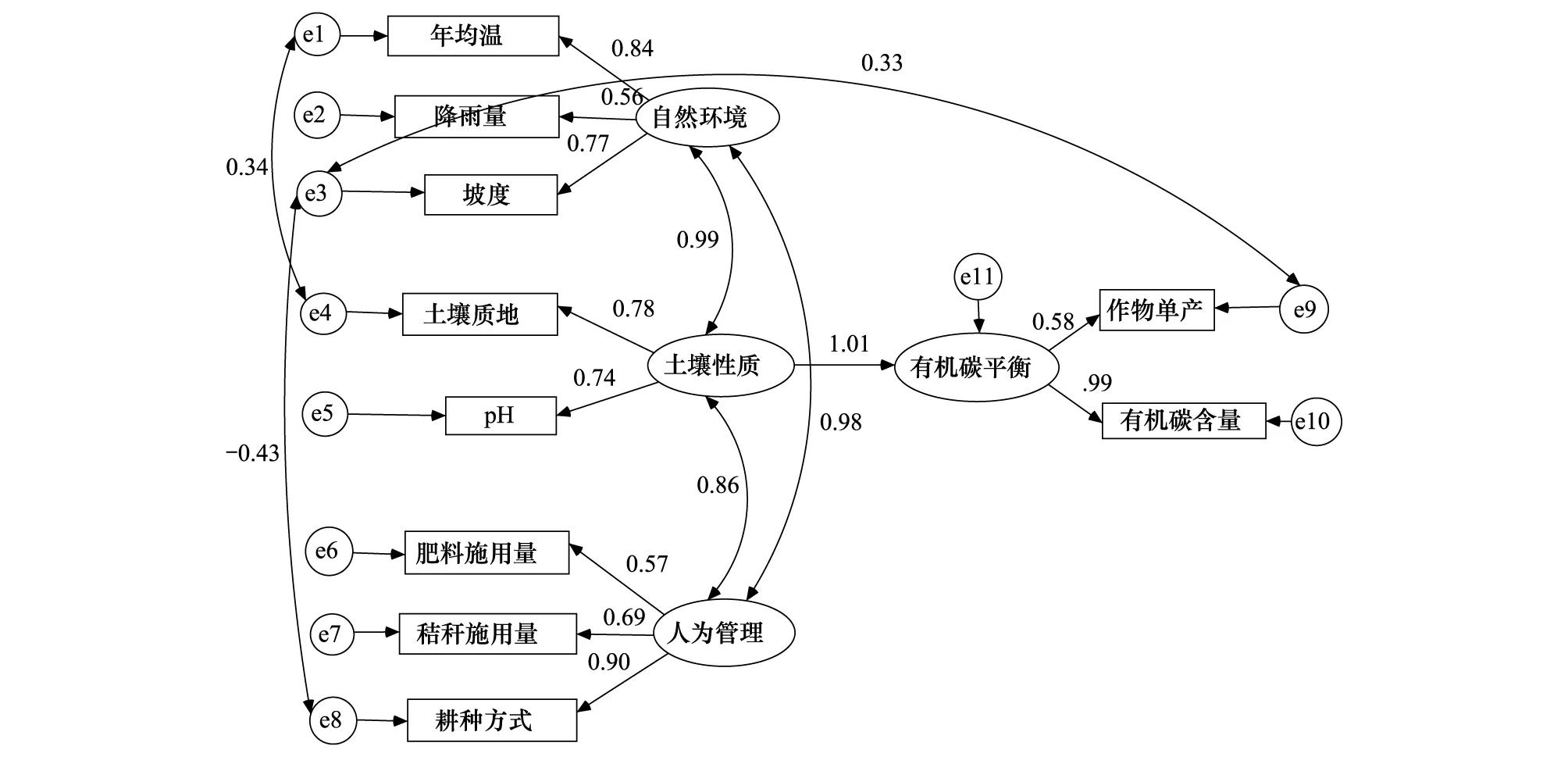
圖4 有機碳平衡關系標準化系數修正模型Fig.4 Standardized coefficients correction model of organic carbon equilibrium

表4 潛變量及可測變量之間總的影響效果情況Table 4 Total effects between latency variables and measurable variables

表5 模型假設結果驗證表Table 5 Verification results of model assumption

表6 擬合指數表Table 6 Fitting coefficients list

3.3 模型計算結果分析

(1)對于有機碳平衡應該重點提升人為管理這一潛變量

土壤性質對有機碳平衡狀態有正向的影響，路徑系數為1.01，影響巨大；自然環境、土壤性質和人為管理具有兩兩相關關系。自然環境與土壤性質的相關系數為0.99，相關性極大，從可測變量中可以看出，年均溫和土壤性質有較大程度的相關性，氣候環境影響著土壤的形成和發展，如降水對其進行著水分的調節與分配，同時土壤自身對氣候環境有著影響；土壤性質與人為管理相關系數為0.86；自然環境與人為管理相關系數為0.98，相關性極大，從可測變量中可以看到，坡度與耕作方式有很大程度的相關性。氣候環境和人為管理對有機碳平衡狀態均為間接效應，其間接影響路徑系數分別為1和0.87，自然環境的間接影響效應大于人為管理的效應，因此，對于有機碳平衡的影響自然環境更大些。這一結論與最初建立模型假設不符，究其原因，主要是在人們常規的認知中，自然環境和人為管理都直接影響著土壤有機碳的變化，但是細究之，不難發現，不論是氣候環境里的溫度、降水和坡度還是人為管理中的肥料施用量、秸稈施用量和耕作制度都是作用在土壤本身，而碳也同樣依附在土壤中，所以自然環境和人為管理都是通過土壤的性質間接地影響著土壤有機碳的平衡。從圖4和上述論述可以得出，土壤性質對土壤有機碳平衡的影響是直接的，路徑系數為1.01，氣候環境和人為管理對有機碳平衡狀態均為間接效應，其間接影響路徑系數分別為1和0.87，氣候環境和土壤性質對有機碳平衡的影響相當高，因此可以說，在未來有機碳平衡研究和實踐過程中，應重點提升人為管理這一潛變量。

(2)反映各個潛變量的可測變量之間存在重要的相互影響的關系

有機碳平衡的過程是一個多因素共同作用的過程，潛變量之間的關系揭示了有機碳平衡的主線，可測變量除了表征潛變量外，相互之間的關系使其間接地影響了相關潛變量，進一步揭示了各個潛變量之間的間接關系。由可測變量之間的互動關系可進一步顯示有機碳平衡過程中各個潛變量所代表的系統之間作用的重點，對潛變量的現狀關系做出進一步解釋[17]。從表4可以看出，可測變量作物產量除了表征有機碳平衡這一潛變量外，同時與土壤性質這一潛變量相關，其影響系數為0.568；而可測變量有機碳含量除了表征有機碳平衡這一潛變量外，對土壤性質也有著間接影響，其影響系數高達0.993。這與土壤性質對有機碳平衡具有正向直接影響的結果相吻合。

(3)表征潛變量的各個可測變量對其潛變量的貢獻程度有差異

從土壤機碳平衡潛變量的兩個可測變量來看，有機碳含量貢獻程度大于作物單產，其路徑系數分別為0.99、0.58，這個與實際情況相符；從自然環境潛變量的兩個可測變量來看，年均溫對于自然環境的貢獻最大，其次為坡度，最后為降雨量，其路徑系數依次為0.84、0.77、0.56，公認溫度對土壤有機碳影響較大，是影響關系和趨勢較為明顯的可測變量；坡度影響著有機碳在空間上的遷移和再分布，也是影響較明顯的可測變量；而降雨量對土壤有機碳平衡影響較為復雜，易受到其他因素的影響；從土壤性質潛變量的兩個可測變量可以看出，土壤質地和pH對土壤性質的表征比較接近，土壤性質略微大于pH,分別為0.77和0.74；對于人為管理這個潛變量，耕種方式這一可測變量影響較大些，其次為秸稈施用量，最后為肥料施用量，其路徑系依次為0.9、0.69、0.57，根據路徑系數的結果判定，應對人為管理這個潛變量中的耕作方式進行更為科學合理的管理，以使有機碳平衡向更高狀態平衡發展。

4 結論與討論

土壤有機碳平衡是一個復雜的動態過程，是潛變量與潛變量、潛變量與可測變量、可測變量與可測變量相互作用的結果。結構方程模型的建立很好地描述了這一復雜關系。本研究通過對東北地區5個典型市縣結構方程模型的建立、運算和分析表明：土壤性質對有機碳平衡具有直接影響作用；在土壤有機碳的平衡過程中，氣候環境、土壤性質和人為管理具有兩兩相關性，且氣候環境和人為管理通過土壤性質傳遞并影響土壤有機碳平衡，氣候環境的影響力大于人為管理的影響力。針對有機碳平衡關系所計算出的路徑系數，需要強化人為管理在土壤有機碳平衡過程中的作用，特別要在耕作方式上加強管理，促使有機碳平衡向更優化方向發展。

當然本研究探索性地將結構方程模型引入了土壤有機碳平衡關系研究中，定量化研究影響有機碳平衡的因素，研究結果是由已有現狀數據所支撐的，是反映當前狀態下的有機碳平衡關系，對于其形成的歷史根源及未來的發展趨勢尚難以定論。因此，對于不同時期、不同尺度和不同條件下的有機碳平衡關系則需要更加完善和翔實指標和調查數據來擬合，從而使結論更具科學性和準確性。

[1] Lal R. World soils and the greenhouse effect. IGBP Global Change Newsletter, 1999, 37: 4- 5.

[2] 潘根興. 中國土壤有機碳庫及其演變與應對氣候變化. 氣候變化研究進展, 2008, 4(5): 282- 289.

[3] 周濤, 史培軍, 王紹強. 氣候變化及人類活動對中國土壤有機碳儲量的影響. 地理學報, 2003, 58(5): 727- 734.

[4] 金峰, 楊浩, 趙其國. 土壤有機碳儲量及影響因素研究進展. 土壤, 2000, (1): 11- 17.

[5] Dalal R C, Carter J O. Soil organic matter dynamics and carbon sequestration in Australian tropical soils//Lal R, Stewart B A, eds. Global Climate Change and Tropical Ecosystems. Advances in Soil Science. CRC Press, Lewis, 2000: 283- 314.

[6] Bottner P, Austrui F, Cortez J, Billès G, Couteaux M M. Decomposition of14C and15N labelled plant material, under controlled conditions, in coniferous forest soils from a north-south climatic sequence in western Europe. Soil Biology and Biochemistry, 1998, 30(5): 597- 610.

[7] Giardina C P, Ryan M G. Evidence that decomposition rates of organic carbon in mineral soil do not vary with temperature. Nature, 2000, 404(6780): 858- 861.

[8] 姜勇, 莊秋麗, 梁文舉. 農田生態系統土壤有機碳庫及其影響因子. 生態學雜志, 2007, 26(2): 278- 285.

[9] 吳兆龍, 丁曉. 結構方程模型的理論、建立與應用. 科技管理研究, 2004, (6): 90- 95.

[10] 王繼軍, 李慧, 蘇鑫, 杜娜. 基于農戶層次的陜北黃土丘陵區農業生態經濟系統耦合關系研究. 自然資源學報, 2010, 25(11): 1887- 1896.

[11] 易丹輝. 結構方程模型方法與應用. 北京: 中國人民大學出版社, 2008.

[12] Wright S. Correlation and causation, Journal of Agricultural Research, 1921, 20: 557- 585.

[13] Pearl J. Causality: Models, Reasoning, and Inference. Cambridge: Cambridge University Press, 2000.

[14] 孫鳳. 主觀幸福感的結構方程模型. 統計研究, 2007, 24(2): 27- 32.

[15] 王雪原, 王宏起. 區域科技創新資源配置系統結構方程模型及模式選擇. 技術經濟, 2008, 27(12): 36- 42.

[16] 李煥榮, 蘇敷勝. 人力資源管理與企業績效關系的實證研究——基于結構方程模型理論. 華東經濟管理, 2009, 23(4): 102- 108.

[17] Brahim N, Blavet D, Gallali T, Bernoux M. Application of structural equation modeling for assessing relationships between organic carbon and soil properties in semiarid Mediterranean region. International Journal of Environmental Science and Technology, 2011, 8(2): 305- 320.

[18] 國家統計局農村社會經濟調查總隊. 2012年中國農村統計年鑒. 北京:中國統計出版社, 2013: 55- 56.

[19] 侯杰泰, 溫忠麟, 成子娟. 結構方程模型及其應用. 北京:教育科學出版社, 2004:123- 178.

Equilibrium relationships of soil organic carbon in the main croplands of northeast china based on structural equation modeling

LI Hui，WANG Jingkuan*，PEI Jiubo，LI Shuangyi

CollegeofLandandEnvironment,ShenyangAgriculturalUniversity,Shenyang110866,China

Soil organic carbon equilibrium (SOCE) is a complex process determined by the interactions between of different latent variables, or between measurable variables, and between the latent and measurable variables. The interaction relationships could be well expressed by the structural equation modeling (SEM). Based on the surface soil (0—20 cm)data of some typical counties (Dunhua, Yushu, Gongzhuling, Changtu and Fuxin) in the Northeast China, a SEM of soil organic carbon equilibrium in those counties was simulated, and the relationships of SOCE as affected by different variables were evaluated. The results indicated that there were significant interactions between latent variables (climate regimes, soil properties and management practices). Soil properties had a direct positive effect on SOCE with a path coefficient 1.01, while climate regimes and management practices influenced on SOCE indirectly through soil properties. Moreover, the influence of climate was greater than that of the management with path coefficients of 1 and 0.87, respectively. According to the path coefficients calculated by the SEM on SOCE, it is very important to pay more attention to the effect of human activities (especially tillage practices), on the process of SOCE and it is extremely crucial to optimize SOCE by a better development.

latent variables; path coefficients; impact factors; tillage practices

國家自然科學基金項目(41171237); 中國科學院戰略性先導科技專項子課題“東北農田土壤固碳潛力與速率研究”(XDA05050501)

2013- 03- 30;

日期:2014- 03- 25

10.5846/stxb201303300562

*通訊作者Corresponding author.E-mail: j-kwang@163.com

李慧，汪景寬，裴久渤，李雙異.基于結構方程模型的東北地區主要旱田土壤有機碳平衡關系研究.生態學報,2015,35(2):517- 525.

Li H，Wang J K，Pei J B，Li S Y.Equilibrium relationships of soil organic carbon in the main croplands of northeast china based on structural equation modeling.Acta Ecologica Sinica,2015,35(2):517- 525.