基于“門到門”運輸的鐵路物流“庫存--運輸”模型研究

湯銀英 李佰城

西南交通大學，交通運輸與物流學院，成都 610031

0 引 言

隨著我國鐵路貨運改革的深入，“全程物流化”既是應對激烈的市場競爭所提出的新措施，也是適應現代物流發展的必要進程。原來的鐵路運輸企業將不僅僅承擔物流系統中的運輸環節，而是逐步轉型為依托鐵路資源的綜合物流企業。因此，物流相關問題的解決辦法也可以嘗試應用在鐵路物流企業決策中[1]。

關于庫存-運輸模型的建立和求解，國內外已有很多學者在相關領域進行了深入的研究和探討。國外對此問題的研究較早開始，Harris于 1913年就提出經典EOQ訂貨模型。之后，針對此問題相關的問題結構、模型條件、求解算法等方面又引起其他學者的興趣。隨著我國對物流業發展的逐步重視，一些具有前瞻性的國內學者也開始對此問題著手研究。杜文（2004）構造了描述此類問題特征的數學模型和有效的啟發式算法，并對隨機需求情況下的庫存與運輸優化問題進行了探討[2]。葉志堅（2003）針對客戶需求小批量、多批次配送的特點，以最小化長期平均期望總成本為優化目的，建立了 VMI模式下的供應商庫存補充和配送整合策略優化模型[3]。張茹秀等（2005）把運輸費率看作是運輸量的非線性函數，在允許缺貨、滿足一定服務水平等條件下，提出價格折扣/運輸折扣的庫存-運輸聯合優化模型[4]。劉立輝（2012）在其著作中對目前庫存-運輸整體優化問題的成果進行了系統的梳理，對四種不同配送網絡分別建立模型、設計算法，并分析了今后的研究方向[5]。

本文將從鐵路物流企業發展角度，建立依托鐵路運輸資源、聯合多種運輸方式的“門到門”庫存-運輸模型，為鐵路物流企業提供全程物流決策支持。

1 問題的描述

本文將鐵路物流企業看作物流系統中的供應商角色，即生產商委托鐵路物流企業將產品（貨物）運送至指定的各個分銷網點。鐵路物流企業雖然擁有一定的倉儲設施和運輸能力，但由于庫存與運輸之間存在“效益悖反”[6]關系，因此，不能片面的追求單方面利益的最大化。此外，鐵路運輸能力也存在指令性波動（如春運、救災等），不同時期、不同線路、不同的車流組織方式所產生的運輸費用也不同。針對上述問題，結合當前鐵路改革“門到門”運輸的發展模式，本文提出建立以鐵路運輸為主導、聯合多種運輸方式的庫存-運輸整體最優模型，確定產品（貨物）在需求與時間呈線性相關條件下物流總費用最小的解決方案。

2 建立庫存-運輸模型

2.1 庫存費用分析

庫存具有緩解供需矛盾、維持正常生產、應付波動需求的作用。在企業的庫存管理中，所確定的物資采購批量不能按計劃執行的現象是屢見不鮮的，或因質量不合格而發生退貨，或因貨源暫時不足而不能如數到貨，或因運輸困難不能按期到貨等。因此，有一定的物資貯存（安全庫存量）尤為重要。

本文考慮的庫存費用主要包括以下費用：

（1）庫存保管平均費用。貨物運到后租賃倉庫及保管貨物的費用。

（2）訂貨費。指向生產商發出采購訂單的成本，包括提出請購單、分析供應商、來料驗收等各項費用。一般視為固定成本，年總訂貨成本隨訂貨次數的減少而減少。

（3）缺貨成本。指由于庫存供應中斷或延遲所產生的延期交貨損失。

2.2 運輸費用分析

運輸時間的長短會影響分銷點的庫存水平（訂貨庫存和安全庫存）。如果選擇運輸費用低且時間長的線路，那么會增加庫存成本；相反，運輸費用高且時間短的線路會抵消庫存成本降低的情況。因此，鐵路物流企業提供的方案中最合理的應該是在滿足運到期限條件下，允許多式聯運，考慮庫存和運輸費用綜合成本最低的一種。

2.3 庫存-運輸模型

本文研究的問題假設：

（1）鐵路貨運站具有自己獨立經營的各類倉儲設施、設備，且容量足夠大；

（2）聯合運輸中不考慮因在銜接處耽擱時間而產生的庫存成本；

（3）考慮貨損、裝卸費及延誤幾率等因素，設定可轉換運輸方式的區段不超過4個；

（4）鐵路必須作為聯運中的一種運輸方式，不考慮鐵路貨運部門制定計劃需提前的時間及車流組織方式；

（5）各種運輸方式在劃定的運輸區段內的運輸時間已知；

（6）本文的訂貨量確定未進行討論，由企業根據自身要求制定相應訂貨策略。

（7）假定生產商的供應量與分銷點的需求量都與時間呈線性相關，且前者單位時間提供的入庫量大于后者單位時間的消耗量。

基于安全庫存量的平均庫存量如下：

安全庫存量：

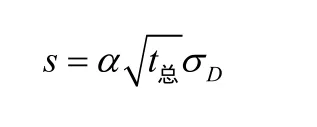
式中：s—— 安全庫存量；

α—— 安全系數，決定于生產中允許缺貨的概率；t總—— 總運輸時間；

D

σ—— 需求量變化偏差值。

平均庫存量：

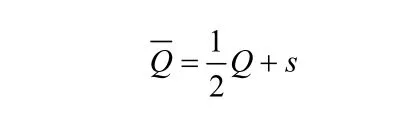
式中：Q—— 平均庫存量；

Q—— 訂貨批量。

平均庫存費用表示為：

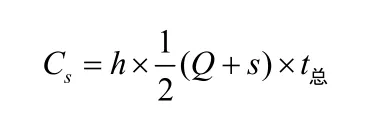
式中：sC—— 平均庫存費用；

h—— 庫存保管費用/單位×時間；

t總—— 總運輸時間。

由于市場存在需求突變的情況，或者由于生產商與供應商之間出現某種問題而供貨中斷或延遲，因此，缺貨費用為

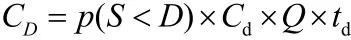
式中：DC—— 缺貨費用；

p(S ＜D)—— 缺貨概率；

S—— 單位時間供應量；

D—— 單位時間需求量；

Cd—— 缺貨成本/單位×時間；td—— 延誤時間。

在運輸過程中可能會出現不同運輸方式之間的轉換，裝卸費在整個運輸過程中不可忽略，甚至可能影響運輸路線的選擇，因此，裝卸費用可表示為：

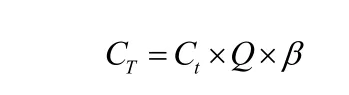
式中：TC—— 裝卸費用；

Ct—— 裝卸費用/單位；

β—— 裝卸次數。

為了方便研究，可以先確定一條路線，建立滿足運到期限內采用多種運輸方式聯運的最低庫存-運輸成本模型[7]。

模型建立如下：

式中：R—— 運輸路線；

r—— 備選運輸路線；

Crail—— 鐵路運輸費用函數；

Croad—— 公路運輸費用函數；

Cship—— 水路運輸費用函數；

Cair—— 航空運輸費用函數；

i—— 運輸區段；

j—— 運輸方式；

σk—— 運輸方式選擇0,1變量；

t裝卸—— 在運輸中的裝卸時間；

t限—— 運輸期限；

tij—— 在i區段采用j運輸方式對應的運輸時間；

Lij—— 在i區段采用j運輸方式對應的運輸里程；

Lr—— 路線r的中運輸里程。

3 模型的特點及求解

3.1 模型的特點

本文建立的模型具有以下特點：

（1）模型表示出由于運輸方式、路線的不同而導致運輸時間不同，所產生的平均庫存費用和缺貨費用也不同，將時間因素作為更好地反映庫存成本與運輸成本“效益悖反”的指標；

（2）考慮鐵路物流發展“門到門”運輸的發展趨勢，采用依托鐵路運輸資源的聯合運輸方式作為解決方案；

（3）模型的可行解是在滿足運輸期限下的方案中產生的，這里體現了鐵路物流企業以客戶需求為服務目標的理念；

（4）本文建立的模型庫存-運輸模型具有“背包問題”的特點，而“背包問題”是一個典型的NP完全問題。求解方法主要有一些啟發式算法，如貪婪算法、蟻群算法等；也可用全局優化方法，如遺傳算法（GA）和模擬退火算法（SA）等。本文探討用模擬退火算法來對其進行求解。

3.2 模型的求解

在求解之前，依貨物的種類和合理的運輸方式劃分運輸區段，并確定鐵路運輸的區段。根據t總≤ t限條件預選出符合條件的路線，同時獲取每條路線每個區段的運輸時間和運輸里程。具體求解步驟如下：

Step 1 令T =t限，即開始退火的初始溫度，隨機生成一個初始解并計算相應的目標函數值 E (σ0)；

Step 2 令T等于冷卻進度表（滿足t總≤ t限的t總值集合）中的下一個值， Ti=t總i，相?應解為目標函數值為 E (σk) ；

Step 3 根據當前解σk進行0-1隨機擾動（即改變運輸方式組合），產生一個新解σ′k，計算相應目標函數值，得到 Δ E = E(σk′ ) - E (σk)；

Step 4 若ΔE＜0，則新解σk′被接受，作為新的當前解；若ΔE＞0，則新解σ′k按概率接受，Ti為當前溫度；

Step 5 在溫度 Ti下，重復 Lk次的擾動和接受過程，即執行步驟Step 3、Step 4；

Step 6 判斷T是否已達到 Tf（收斂條件），是，則終止算法；否，則轉到Step 2繼續執行。

3.3 模型的拓展

上述模型適合于一般大宗穩定貨物企業與鐵路運輸企業長期合作下的運輸方案制定。然而，若考慮運輸不均衡或需求波動，則是另外一種情形。鐵路上引起運輸不均衡的因素有很多，如運輸市場需求的不斷變化引起日裝車量的波動、客貨運力調整、鐵路運能限制、施工及運輸設備維修、行車事故、特殊氣候及自然災害影響等，而這將直接導致停時增大，影響鐵路運輸效益[7]。

鐵路運輸企業應對貨運需求突然增加有車種代用、增調空車兩種措施，為了保證鐵路運輸的時效性，即使出現貨運需求突然減少，也允許欠軸編發列車。由于目前鐵路貨運營銷的強制性，本文考慮貨源突然減少是由于貨主造成的（有些鐵路局甚至把貨源減少作為考核指標），且認為前述缺貨成本已考慮此種情況，故不作重復討論。從鐵路運輸企業角度看，當發生貨源突然增加情況時將采取合理應對措施來盡可能降低運輸成本，其他運輸方式應對策略類似。因此，模型還應加入貨運需求突然增加導致的額外運輸成本（本文以鐵路為例，其他運輸方式有相應的調整策略）：

目前關于鐵路車種代用和增調空車的運輸成本研究文獻不少，且涉及到運輸路徑的優化、運輸時間成本、機會成本等因素，本文不再做深入分析。

4 算例分析

一批600 t貨物需從生產企業a地運往b地，其中 b地為一港口，且公路、鐵路可進入港區。a、b之間鐵路運輸里程1 500 km，假設公路與鐵路基本平行。有一港口C，距b地水運距離800 km，a地至b地路線示意圖如圖1所示，相關參數設定如表1所示。為方便研究，簡化三種運輸方式的費用函數，以鐵路為基準，平均每噸公里運費按 0.15元計，水路和公路平均每噸公里運費分別為其1/2和3倍計。另外，每次運輸方式轉換即換裝時，假定增加總運輸時間12 h，并產生裝卸費15元/t。

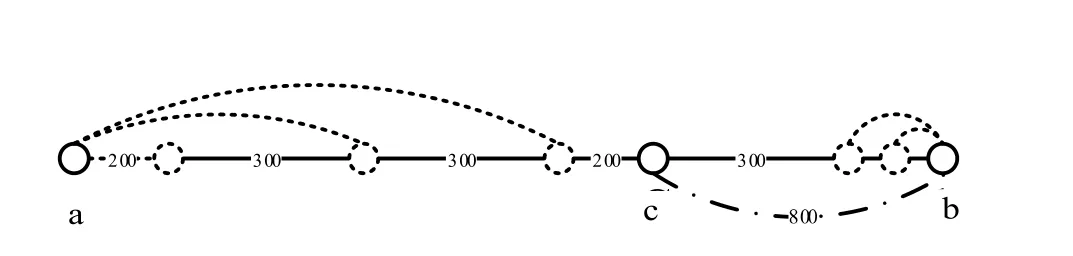
圖1 a-b兩地交通示意Fig.1 Transportation demanstration between places a and b

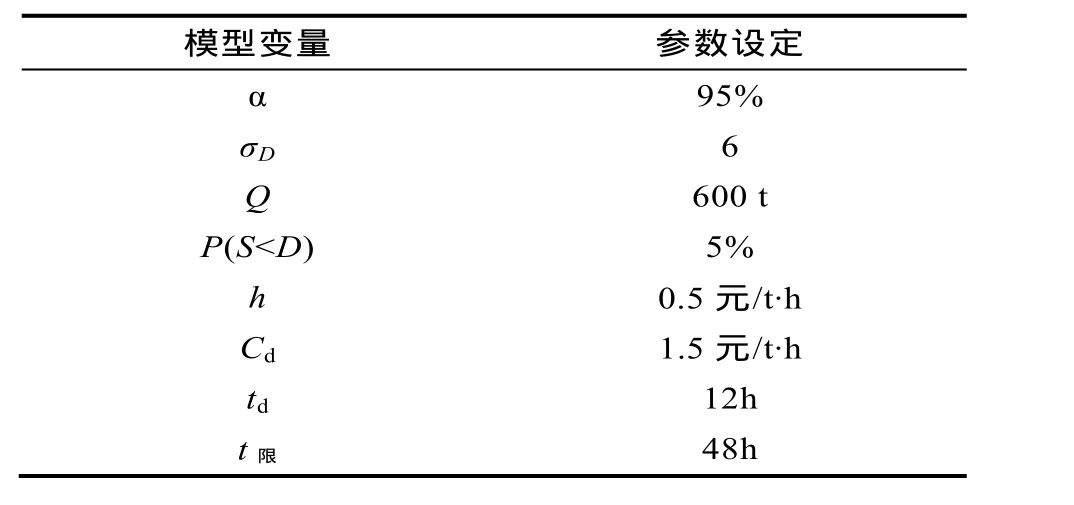
表1 算例相關參數設定Tab.1 Relative factors of the example

通過模型求解，得到最優貨物運輸方案為：由公路運輸至距a地200 km的鐵路貨運站，換裝后直接由鐵路運輸至b地，全程耗時41 h，運費約18.71萬元。

在模型求解過程中，若考慮時間最短的貨物運輸方案為：由公路運輸至C地，再鐵路運輸至b地，全程耗時37 h，但其花費約33.04萬元，是運費最優方案的1.7倍。如何在運輸時間與運費之間尋找最優方案，取決于貨主對該批貨物的時間價值和經濟價值的考量。

5 結論及建議

本文考慮了鐵路物流企業“門到門”運輸的服務模式，通過對庫存費用和運輸費用分析，建立了在滿足運到期限條件下、依托鐵路資源的多式聯運庫存-運輸聯合最優模型，并給出了采用模擬退火算法的求解步驟。

結合實際工作對模型的變量進行分析，我國鐵路物流企業還應在以下幾個方面著手改進以取得更多效益。一是改善鐵路貨運工作組織，調整貨物集疏運方式，縮短貨物在途時間，并通過車流優化等手段降低發生晚點幾率；二是對全程運輸中鐵路運程的運價進行合理調整，吸引更多的客戶；三是建立綜合型物流中心，并完善快捷鐵路物流網絡（包括運輸設施網絡、物流信息網絡和營銷網絡），使鐵路運輸資源有效發揮網絡經濟性。

[1] Tang Yinying, Li Baicheng. Multimodal transport based on inventory-transport integrated optimization model [C]. Chengdu，China：Proceedings of The 2014 International Conference of Logistics Engineering and Management，1437-1442.

[2] 杜 文，袁慶達，周再玲. 一類隨機庫存/運輸聯合優化問題求解過程分析[J]. 中國公路報，2004，17(1):114-118.

[3] 葉志堅，杜 文，王清榮，朱健梅. 供應商管理庫存系統中庫存和運輸計劃整合[J]. 交通運輸系統工程與信息，2003，3(4):82-88.

[4] 張茹秀，徐天芳. 價格折扣/運輸折扣的庫存-運輸聯合優化模型[J]. 大連海事大學學報，2005，31(3):41-44.

[5] 劉立輝. 庫存與運輸整合優化問題研究[M].濟南：山東大學出版社，2012.

[6] 譚 惠，湯銀英. 基于供應鏈管理的鋼鐵企業庫存與運輸整合優化研究[J]. 物流技術，2009，28(11):185-187.

[7] Masami Amano，Takayuki Yoshizumi，Hiroyuki Okano. The modal-shift transportation planning problem and its fast steepest descent algorithm[C].New Orleans，USA：Proceedings of the 2003 Winter Simulation Conference, 1720-1728.