基于數學模型的變形鎂合金AZ31B熱力學及動態再結晶

常玉寶，李詩軍

（1.白城師范學院 數學學院，吉林 白城 137000；2.湖南華菱湘潭鋼鐵有限公司，湖南 湘潭411100）

0 前言

純鎂及鎂合金密度非常小，是目前最輕的金屬結構材料，同時它具有比剛度和比強度高、阻尼減振性好及電磁屏蔽性強等諸多特點。鎂合金被認為是21世紀最具發展潛力的金屬材料之一，被廣泛應用于航空航天、汽車工業和醫療等領域[1]。國內外很多有色金屬研究學者為了揭示鎂合金塑性成型的規律和特點，進行了很多關于鎂合金塑性變形理論方面的研究。包括鎂合金位錯交滑移的特征和機制（如割階—配對機制、Friedel機制及鎖定—解鎖機制）；滑移特征及其影響因素（如變形速度、變形溫度、合金元素及晶粒度等）；孿生模式、孿晶與滑移之間及孿晶與孿晶之間的交互作用、塑性變形中孿生的作用及影響因素（如變形溫度、應變速率、晶粒取向及尺寸等）[2-4]。

鑄軋鎂板在現代軋制工藝中晶粒尺寸較為粗大，而細化鎂合金中晶粒的手段之一就是軋制鑄軋鎂板。溫度較低時，軋制容易導致邊裂，這種邊裂是由晶界處產生孿晶位錯形成的位錯塞積累到一定程度后發生的。為了降低軋制鎂板的邊裂現象，研究和控制在一定熱變形條件下鎂合金的動態再結晶具有重要的意義。

1 實驗材料和方法

實驗用鑄態AZ31B鎂合金主要化學成分如表1所示。

表1 鎂合金的化學成分 %

熱壓縮實驗加工如圖1所示，圓柱試樣如圖2所示。實驗在Cleeble-1500D熱模擬實驗機上進行，試樣分別在不同的應變速率（0.005s-1、0.05s-1、0.5s-1）和不同溫度（300℃、350℃、400℃）下進行壓縮，變形量60%。實驗加熱區域15 mm，取10℃/s的升溫速率，保溫后連續壓縮變形，為保持高溫時的再結晶組織，變形后采用水激冷。

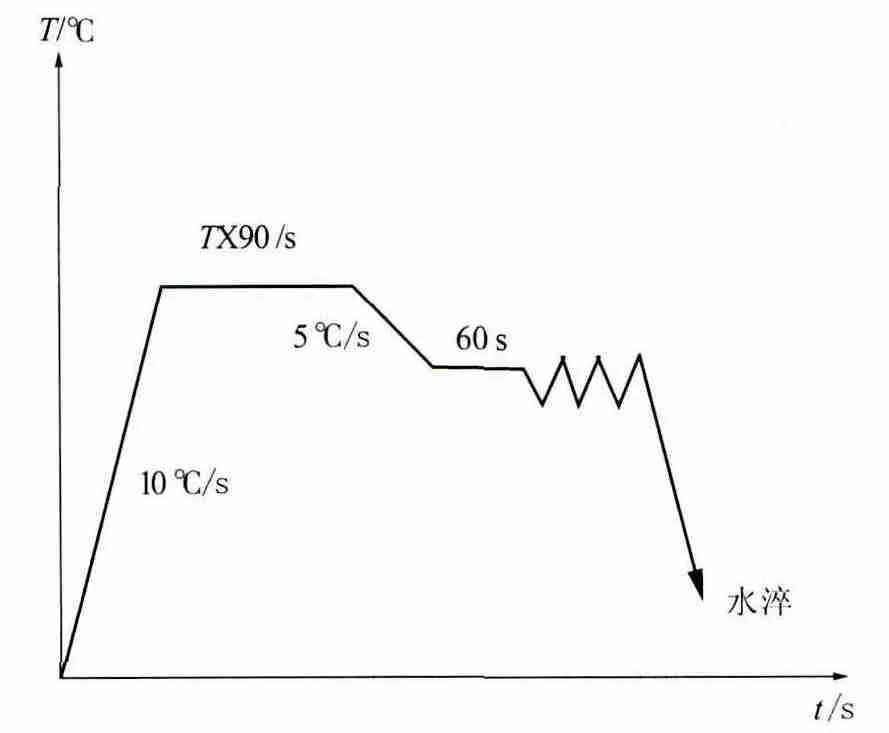
圖1 壓縮實驗加工

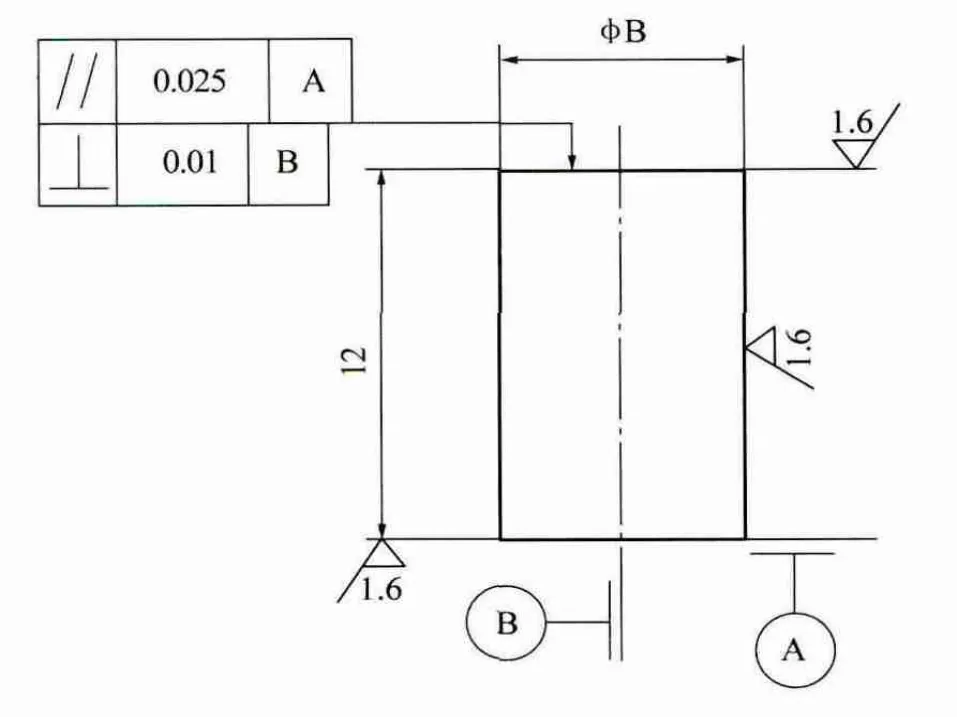
圖2 試樣

2 實驗結果和分析

2.1 應力應變分析

溫度相同時，不同應變速率下的應力-應變曲線如圖3所示；應變速率相同時，不同溫度下的應力-應變曲線如圖4所示。由圖可知，同一溫度下，峰值應力隨著應變速率的增大而增大，高溫狀態下流動應力要比低溫狀態下的屈服應力小，低應變速率相對的應力經過峰值后變化趨于平緩，高應變速率流動應力曲線的波峰形狀在400℃時最為明顯，斜率在彈性變形階段最大。應變速度相同的情況下，溫度越低，波峰形狀越明顯，峰值應力越大。隨著溫度的升高，應力-應變曲線變化趨勢變得比較平緩。鎂合金在較低的應變速率和較高的變形溫度下擁有較高的變形激活能，在熱變形過程中有利于動態再結晶的發生，從而促進熱變形。

2.2 建立與驗證熱變形本構方程

由于溫度變化范圍較大，可用修正后的Arrhenius方程模型來構建AZ31B鎂合金在高溫下產生的塑性形變的流動應力、溫度和應變速率之間的關系[5]

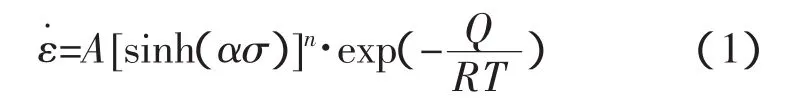
高應力情況下，當 ασ＞1 時，sinh（ασ）≈eασ/2，可將式（1）簡化為

綜合各式，經回歸運算求解，得：A=15.212 6；Q=68 581.35；n=10.85；α=0.001 1；β=0.237 8。因此在應變速率 0.005～0.5 s-1，變形溫度 300 ℃～400 ℃的情況下：

當 ασ＞1時，

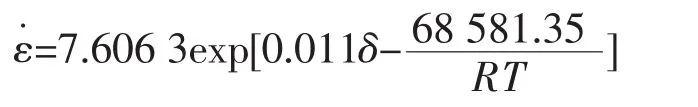
當ασ＜1時，

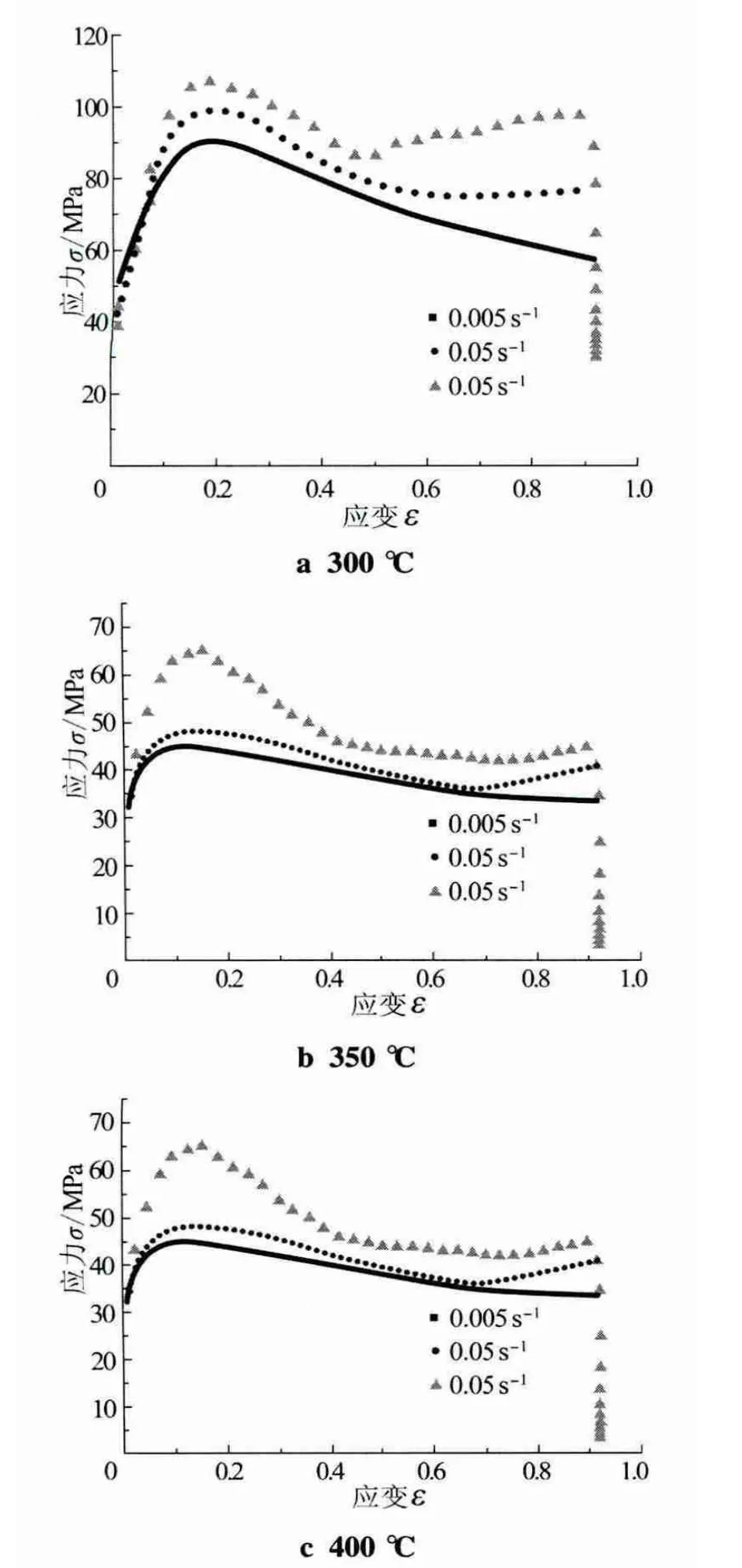
圖3 不同應變速率下的應力—應變曲線

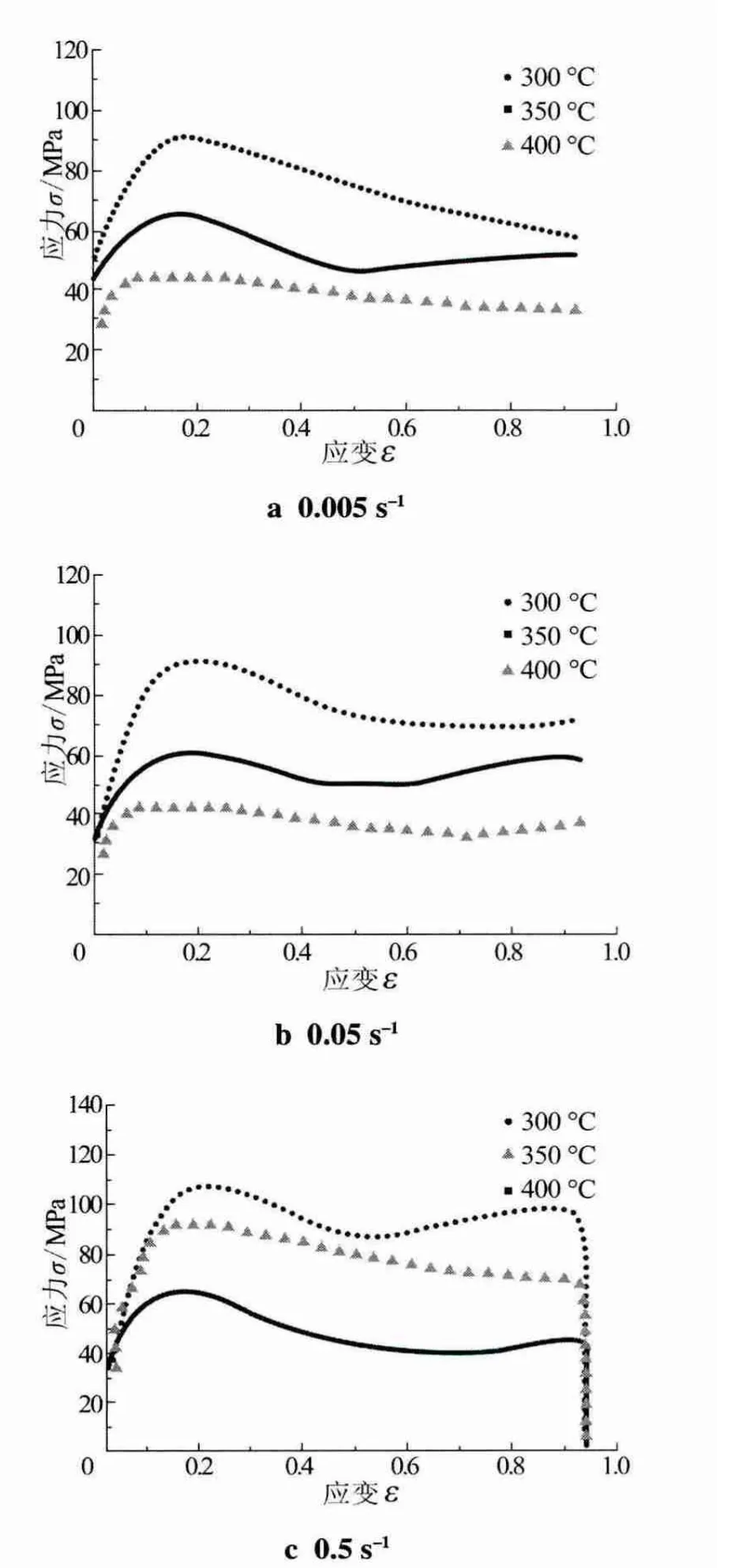
圖4 不同溫度下的應力—應變曲線

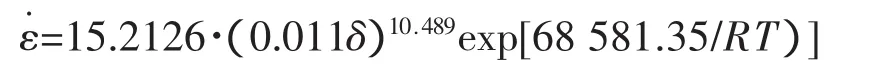
當ασ為任意值時，

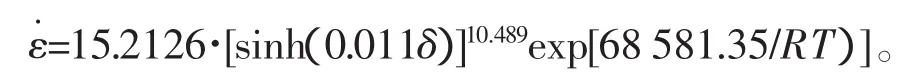
Zener-Hollomon變形因子參數為

圖5為應變速率相同時，不同溫度下計算值與實驗值的對比；圖6為變形溫度相同時，不同應變速率下的計算值與實驗值的對比。圖中試驗值曲線上和計算曲線上的點距離越近，表示誤差越小，可知在應變速率為0.005～0.5 s-1，變形溫度300℃～400℃的條件下，計算值和測量值之間的誤差在0.14%～9.12%之間。

2.3 建立動態再結晶熱力學模型

在實際的熱變形模擬實驗中，鑄態AZ31B鎂合金會交替發生孿生和位錯，根據壓縮試樣的尺寸和加熱區域，其在冷變形中發生動態孿生的可能基本消除，保溫90 s后水淬使得在晶相實驗中觀察到的組織形貌比較真實。壓縮過程中只考慮動態再結晶和位錯行為，動態再結晶熱力學模型采用Cahn提出的[6]

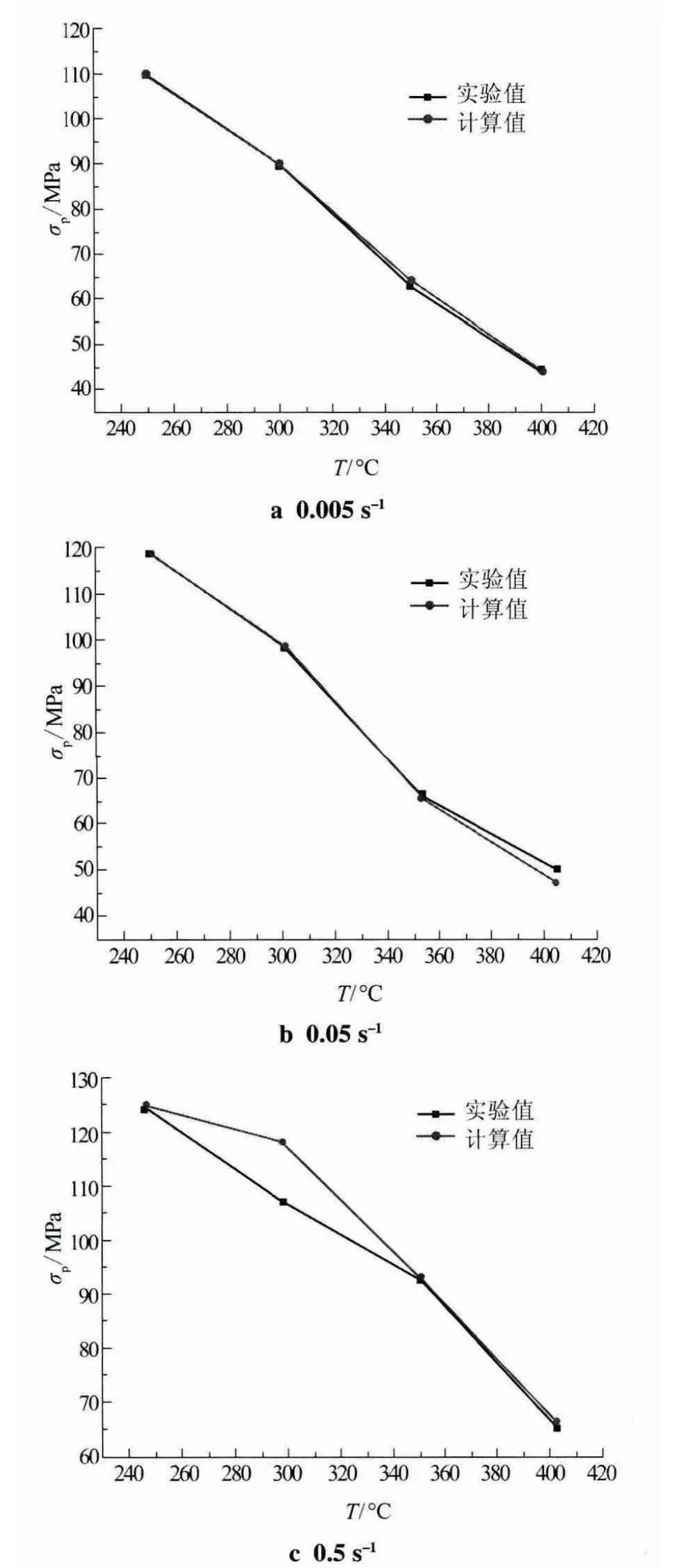
圖5 不同溫度下計算值與實驗值的對比

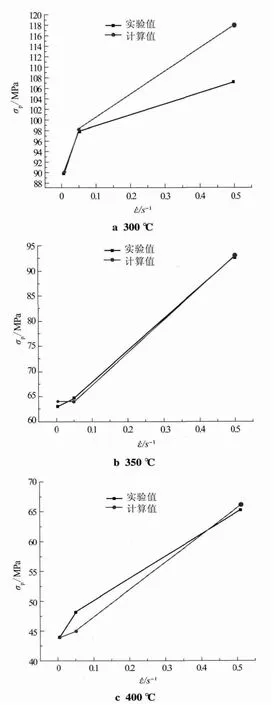
圖6 不同應變速率下的計算值與實驗值的對比

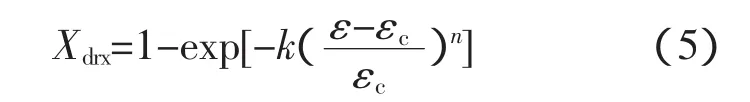
式中 k為材料常數；n為Avrami指數。Yang提出材料內部的位錯密度在動態再結晶發生的過程中可表示為

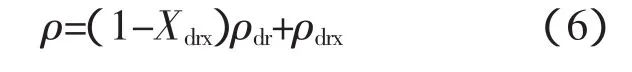
Mcclintock和Bussonoand提出位錯密度與流動應力之間的關系為

式中 σ為流動應力；λ為材料常數；μ為剪切模量；b為伯格斯矢量。

由式（6）和式（7）可得出動態再結晶的體積分數為

式中 Xdrx為動態再結晶體積分數；σdr為發生加工硬化和動態回復的流動應力；σdrx為動態再結晶流動應力，σdr和σdrx可以根據P-J法確定。

AZ31B鎂合金在熱變形過程中，只有當應變量達到動態再結晶的臨界應變值時才會產生動態再結晶。在熱變形過程中AZ31B鎂合金受熱發生軟化，在較低應變速率和較高變形溫度下能夠獲得較高的變形激活能，在熱變形過程中有利于動態再結晶的發生，更有利于熱成形。

2.3 建立及驗證動態再結晶晶粒尺寸模型

動態再結晶晶粒尺寸計算采用下列模型

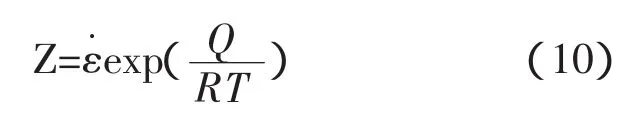
式中 n和A均為材料常數。

對式（10）兩邊同時取對數得

根據線性回歸，求解得到n1=-0.02，A1=3.03，進而可知Z=1.23×10-8σp16.63，所以晶粒直徑尺寸數學模型為ddrx=6.91σp-0.33。Z參數可由計算結果求得，它闡述了變形溫度和應變速率對動態再結晶晶粒尺寸的影響，晶粒的直徑隨著參數Z的增大而減小，形狀越細。

圖7為動態再結晶微觀組織，圖8為在不同應變速率下計算值和實驗值的對比，圖9為在不同溫度下計算值和實驗值的對比（見下頁）。由圖7可知，鎂合金在熱壓縮變形下晶界處會產生動態再結晶組織，原先的鑄態晶粒也會在熱變形過程中因受熱進一步長大；由圖8和圖9可知，分別在不同變形速率和不同變形溫度下將動態再結晶晶粒尺寸的計算值與實驗值進行對比與相對誤差計算，得出誤差為3.59%～11.9%。

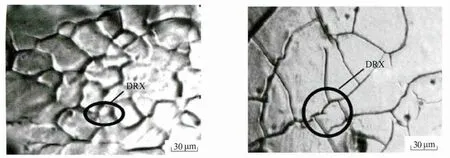
圖7 動態再結晶微觀組織

4 結論

對鑄態AZ31B鎂合金試樣在實驗機上分別在不同的應變速率和變形溫度下進行了壓縮實驗，得到了應力-應變曲線。應變速率一定時，峰值應力隨溫度升高而降低；變形溫度一定時，峰值應力隨應變速率加快而增大。

在對應力-應變數據進行線性回歸處理的基礎上，建立了AZ31B鎂合金變形過程中的各種數學模型，包括熱變形本構方程、動態再結晶熱力學模型和動態再結晶晶粒尺寸模型；最后還基于熱變形實驗數據驗證了AZ31B鎂合金的上述數學模型，熱變形本構方程和動態再結晶晶粒尺寸模型的誤差分別為0.14%～9.12%和3.59%～11.9%。

[1]龐志寧，馬立峰，馬自勇，等.鑄態AZ31B鎂合金熱變形研究[J].熱加工工藝，2014（4）：113-116.

[2]郭強，嚴紅革，陳振華.AZ31鎂合金高溫熱壓縮變形特性[J].中國有色金屬學報，2005（6）：9005-906.

[3]陳振華.變形鎂合金[M].北京：化學工業出版社，2005：72-73.

[4]付雪松，陳國清，王中奇.AZ31鎂合金熱軋變形的動態再結晶機制[J].稀有金屬材料與工程，2011（9）：1369-1375.

[5]王忠堂，張士宏.AZ31鎂合金熱變形本構方程[J].中國有色金屬，2008（11）：36-39.

[6]王健.基于位錯密度變化的動態再結晶動力學確定方法[J].塑性工程學報，2009（4）：163-167.

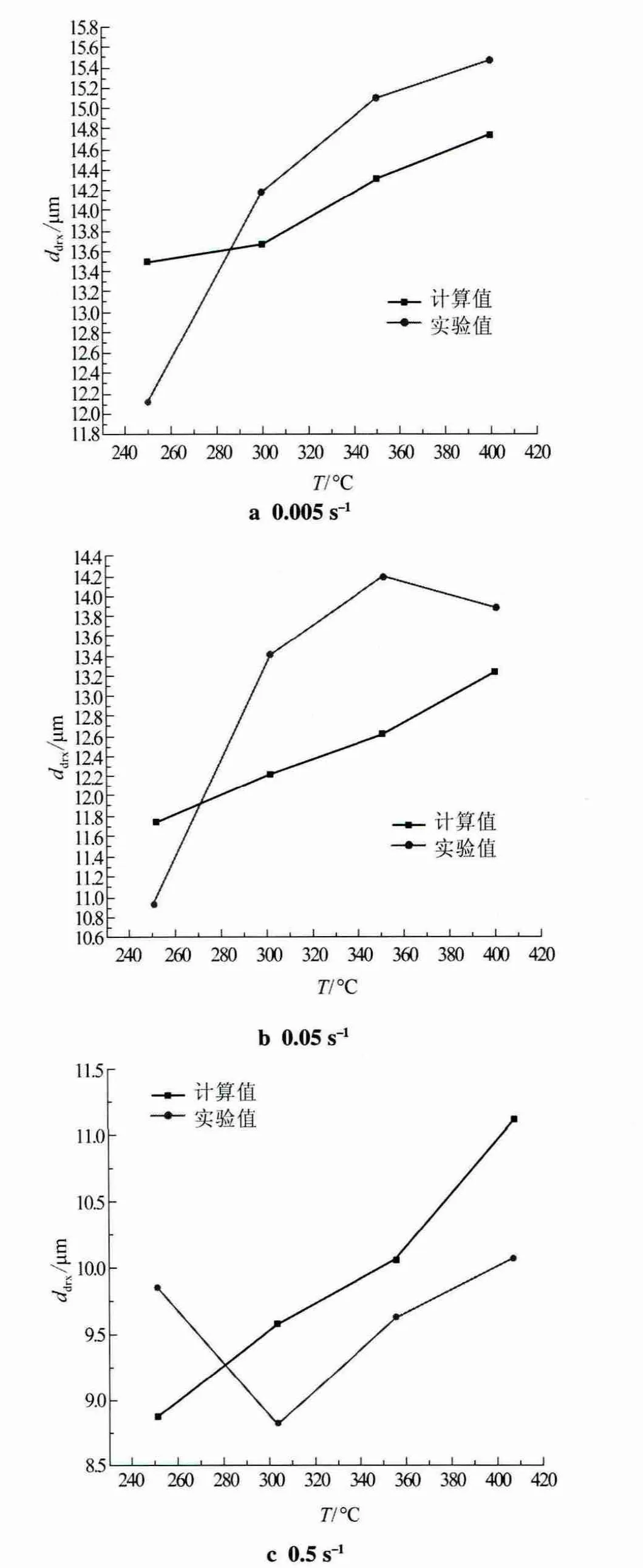
圖8 不同應變速率下計算值與實驗值的對比

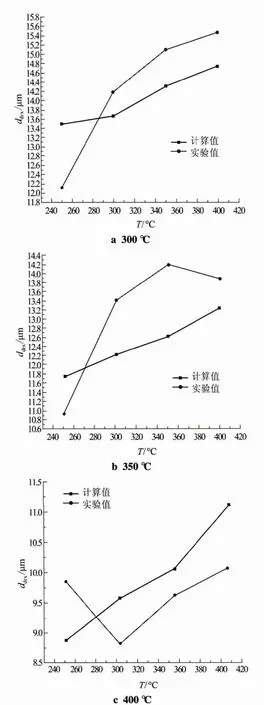
圖9 不同溫度下的計算值與實驗值的對比