歸一化的魯棒性盲水印技術

陳 青，張小亮，馬文君

（上海理工大學光電信息與計算機工程學院，上海200093）

0 引 言

在當今的信息時代，網絡通信等高速傳播途徑日新月異，多媒體產品也隨之進入鼎盛時期，對每日幾何級數激增的龐大多媒體數據的版權保護與真偽認證，面臨極為嚴峻的挑戰。隨著近幾年多媒體保護技術的發展，數字水印以其獨特的優越性成為解決多媒體版權保護的有效手段［1，2］，也成為當今信息安全等領域研究的熱點。

針對魯棒性水印技術面臨的抗幾何攻擊難題，現有文獻對抗幾何攻擊做出了研究［3-11］，算法對抗幾何攻擊的魯棒性水印技術還存在不足，文獻［7］～ ［9］算法雖能抵抗常見攻擊和旋轉攻擊，但未能抵抗拉伸攻擊。因此本文針對載體圖像，在重點研究魯棒水印的基礎上，結合歸一化算法的特性，并根據人眼視覺特點，對魯棒水印技術進行深入的研究，使算法抵抗拉伸及旋轉攻擊。

本文算法結合小波變換技術，在小波變換中，設計的水印系統可以結合載體圖像的空間特點與頻率特性選擇合適的子帶系數，更好地解決了隱蔽性與魯棒性之間的矛盾。由于小波變換本身并不具有抵抗幾何攻擊的性能，因而利用對幾何攻擊具有不變性的歸一化技術來增強水印系統的魯棒性。

本論文的算法利用圖像歸一化所具有的幾何不變性，來抵抗同步攻擊，特別是拉伸攻擊。為驗證所提出算法的魯棒性，采用噪聲、濾波、壓縮等常見的攻擊，并對嵌入實驗圖像進行同步攻擊。實驗結果顯示，該算法具有盲提取特性，提取時不需要載體圖像，且具有良好的隱蔽性、通用性和抵抗常規信號的處理能力，特別對拉伸、旋轉等同步破壞具有較強的魯棒性。

1 魯棒性水印算法設計

1.1 歸一化技術

恢復同步是受幾何攻擊后載體圖像面臨的最大困難，為了能更好地提取水印，很多專家學者利用載體圖像自身特性進行同步，即將水印信號加載到載體圖像內容相關的位置，其中最典型的是圖像歸一化技術。

圖像歸一化技術（Image Nor malization）是一種在模式識別領域已被經常使用的預處理手段。其主要方法是先計算載體圖像的不變矩，在計算的矩中，選取能消除對載體圖像影響的變換矩陣，用其對原始載體進行變換，得到唯一的標準形式。主要處理步驟：

（1）圖像中心化

假設原始圖像W（x1，y1），則對其中心化后的圖像W’（x2，y2），可表示為：

式中，k00、k10、k01均為原始載體圖像W（x1，y1）的幾何矩，其求解公式可表示為：

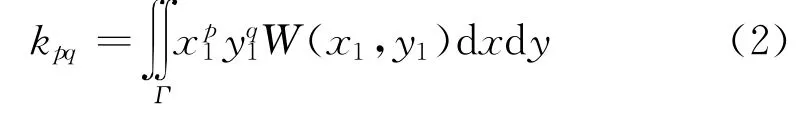
（2）橫軸拉伸

對中心化后的圖像進行拉伸，假設橫軸拉伸后的圖像為W”（x3，y3），則可表示為：

式中，J11、J02是中心化后的圖像W’（x2，y2）的中心距，其求解公式可表示為：

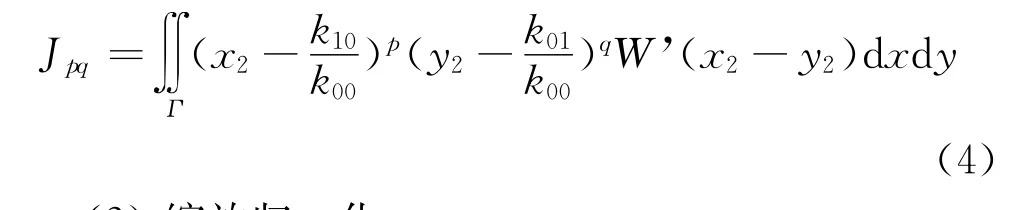
（3）縮放歸一化

對拉伸后的圖像執行縮放歸一化，假設縮放歸一化后的圖像為W?（x4，y4），則可表示為：

式中，I20、I02均為橫軸拉伸后的圖像W″（x3，y3）的中心距。

（4）旋轉歸一化

對縮放歸一化后的圖像進行旋轉歸一化，假設旋轉歸一化后的圖像為W（4）（x5，y5），則可表示為：

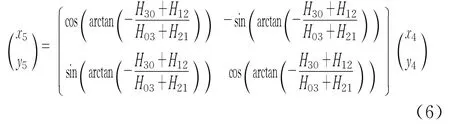
式中，H30、H03、H21和H12均為縮放歸一化后圖像W?（x4，y4）的中心距。

經過上述步驟的處理就可以得到正向歸一化后具有一定位置、方向和大小的標準圖像，為水印信息的嵌入做好準備。

1.2 Arnold變換

Arnold映射是混沌變換的一種，也被稱為貓臉變換，是由V.I.Arnold在研究遍歷理論時提出的。其變換是在空間域里，將載體圖像中的點（x，y）移動到載體圖像中的（x’，y’）位置，并使原本相鄰的點（x，y）和（x，y＋1）經過幾次迭代后不再相鄰，其映射方式如下：

式中，mod N表示模N運算，N×N為圖像的尺寸大小。

Ar nold映射還具有周期性，在一定的迭代次數后，會恢復原始載體圖像各像素點的位置。

1.3 魯棒水印嵌入算法

（1）對一幅N×N的原始載體圖像ZW使用正向歸一化操作，得到正向歸一化變換后的圖像GZW；

（2）利用5／3整數小波變換，對正向歸一化變換后的圖像GZW進行三級小波分解，獲得10個高低頻子帶的變換系數；

（3）通過Arnold映射變換，把原始的黑白二值水印信號Wm，進行k次加密置亂操作，獲得次數密鑰K和映射置亂后的待嵌入水印信號記為Wm’；

（4）提取正向歸一化變換后圖像GZW經過三級小波分解后的HL2、LH2子帶系數，分別提取感興趣重要區域記為HL2’和LH2’；

（5）設定偽隨機函數輸入值num，得到偽隨機序列并轉化為隨機嵌入模板Mv；

（6）對提取的感興趣區域HL2’和LH2’，設其中對應的小波系數分別為CHLi和CLHi；根據隨機嵌入模板Mv，若W＇mk＝1，且Diff＝CHLi-CLHi＜Th，則根據水印信號W＇mk，提升系數CHLi的值，降低系數CLHi的值，使其滿足CHLi-CLHi≥Th，有：

若Diff＝CHLi-CLHi≥Th，則不改變原本系數CHLi和CLHi的值；

若W＇mk＝0，且Diff＝CLHi-CHLi＜Th，則根據水印信號W＇mk，降低系數CHLi的值，提升系數CLHi的值，使其滿足CLHi-CHLi≥Th，有：

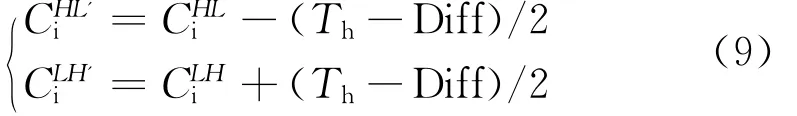
若Diff＝CLHi-CHLi≥Th，則不改變原本系數CHLi和CLHi的值；

（7）對應的系數嵌入完成后，對修改后的子帶系數進行對應的三級5／3小波重構，并進行逆向歸一化處理，得到包含水印的載體記為ZW’。

1.4 盲水印提取算法

數字水印的提取過程與嵌入是逆向過程。特別要指出的是本文中的魯棒水印算法是盲水印算法。提取算法的具體步驟如下：

（1）將受到攻擊后的載體執行正向歸一化，并利用5／3變換，對正向歸一化變換后的圖像進行三級小波分解，獲得LL3、HLn、LHn高低頻子帶的變換系數（n＝1，2，3）；

（2）假設HL2、LH2子帶對應的小波系數分別為CHLi和CLHi，結合偽隨機嵌入模板Mv，提取魯棒水印信號記為Wm?，則有：

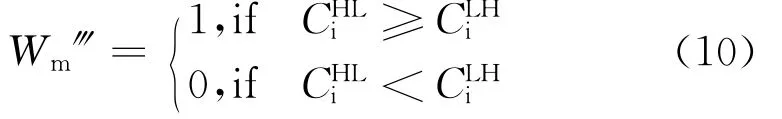
（3）由置亂密鑰k，對提取的魯棒水印進行逆向Arnold到最終的恢復水印記為Wm?。

2 實驗結果分析

圖1 原始載體圖像，水印圖像，正向歸一化后三級小波分解圖像及嵌入水印和提取水印圖像

表1 含水印圖像經過多種攻擊后提取水印

魯棒性的盲水印算法對一幅N＝512，即512×512的8-bit灰度圖像lena（圖1（a））進行實驗，對其使用正向歸一化操作，并進行三級小波分解（如圖像1（c）），水印圖像采用34×34二值圖像。實驗設置：Arnold映射置亂次數為6次，嵌入強度Th設置為10。

2.1 魯棒性實驗

為了驗證水印魯棒性，對含水印圖像進行噪聲、濾波、壓縮及同步性攻擊（尺度變換、旋轉、拉伸），攻擊后提取水印的實驗結果如表1所示。

對含水印圖像進行任意角度旋轉攻擊，并提取水印信息，當旋轉角度為1°時，NC值較高達到0.9215，當進行任意大角度（9°～315°）旋轉攻擊，相關系數（NC）也均在0.82以上。旋轉角度與NC值如圖2所示。

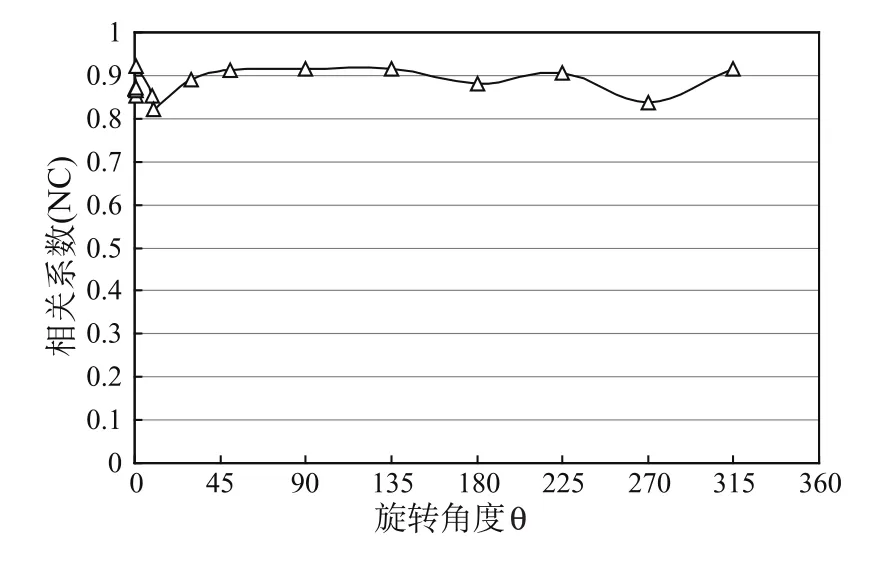
圖2 旋轉角度與提取水印NC值

拉伸攻擊（Shearing Attack）分為：直拉伸和斜拉伸兩種。當載體圖像發生斜拉伸攻擊時，其魯棒水印不僅可能受到寬（X軸方向）和高（Y軸方向）的破壞，還可能會受到主、副對角線上破壞，導致水印信息難以被同步，使水印系統失效。

實驗對含水印Lena圖像采用橫向（X軸方向）、縱向Y軸方向）和主、副對角線方向三種斜拉伸攻擊，提取的魯棒水印如表2所示。其受攻擊后的歸一化相關系數NC的變化范圍分別為0.8875～0.8136。

表2 各種拉伸攻擊及提取水印圖像

3 結 論

本文對魯棒水印進行研究，在整數小波變換域里實現其算法。通過對載體圖像進行歸一化處理，并將歸一化后的載體圖像進行三級5／3整數小波分解，分解后得到相關子帶系數，借助偽隨機模板嵌入置亂后的水印信息，從而形成歸一化魯棒性水印算法。將含水印圖像進行各種攻擊，依然能夠盲提取到水印圖像。實驗結果表明，在滿足不可見性與通用性的前提下，算法能抵抗常規性攻擊（噪聲、濾波、壓縮）和同步性攻擊（尺度變換、旋轉、拉伸），具有很好的魯棒性能和價值。

［1］ Hartung F.Multimedia water marking techniques［C］.Proceedings of the IEEE，1999：1079-1107.

［2］ Cox I J，Kilian J，Leighton T，et al.Secure spread spectrum water marking for multimedia［J］.IEEE Trans on Image Processing，1997，6（12）：1673-1687.

［3］ Dandan Zhu.A new image water marking algorithm using CT and nor malization［C］.Systems，Man，and Cybernetics（SMC），2012 IEEEInternational Conference on.14-17 Oct.2012：3239 3244.

［4］ Liu Ping Feng，Jia Xu，Liang Bin Zheng.A nor malization-based robust digital water marking scheme using nonsub-sampled contourlet transfor m［C］.Electronics Communications and Control（ICECC），2011 International Conference.9-11 Sept.2011：1244-1247.

［5］ Wen Zhan.Wavelet domain geometrically robust image water marking algorithm based on nor malization［C］.Mechatronic Science，Electric Engineering and Computer（MEC），2011 International Conference on 19-22 Aug.2011：1915-1917.

［6］ Dong P，Brankov JG，Galatsanos NP，et al.Digital water marking robust to geometric distortions ［J］.IEEE Transactions on Image Processing，2005，14（12）：2140-2150.

［7］ Duong D M.A nor malization based robust image watermarking scheme in Contourlet domain［C］.Image and Signal Processing（CISP），2013 6th International Congress on（Volume：01），2013：490-495.

［8］ 耿紅琴，張 飛.基于圖像歸一化的數字水印嵌入算法研究［J］.電子測試，2013，7（14）：35-37.

［9］ 盧 鵬，劉 真.基于歸一化的全水印技術［J］.包裝工程，2013，34（1）：01.