B2C電商環(huán)境下集中式退貨中心的車輛調(diào)度

張新艷，周 健，林 婷

（同濟(jì)大學(xué) 機(jī)械與能源工程學(xué)院，上海201800）

隨著網(wǎng)絡(luò)購(gòu)物環(huán)境、政府監(jiān)管及物流環(huán)境等因素的日趨完善與成熟，中國(guó)網(wǎng)絡(luò)零售市場(chǎng)交易規(guī)模和用戶規(guī)模近些年一直呈現(xiàn)持續(xù)增長(zhǎng)狀態(tài).中國(guó)電子商務(wù)研究中心檢測(cè)數(shù)據(jù)顯示，預(yù)計(jì)2014年年底中國(guó)網(wǎng)絡(luò)購(gòu)物用戶規(guī)模將達(dá)到3.9億人.截止2014年6月底，中國(guó)網(wǎng)絡(luò)零售市場(chǎng)交易規(guī)模已占社會(huì)消費(fèi)品零售總額的8.7%，2013年上半年達(dá)到6.8%，同比增長(zhǎng)27.9%，預(yù)計(jì)2014年年底中國(guó)網(wǎng)絡(luò)零售市場(chǎng)規(guī)模將達(dá)到27 861億元.

網(wǎng)購(gòu)的虛擬性、信息不對(duì)稱以及正向物流的不完善等因素導(dǎo)致大量的退貨逆向物流.中國(guó)電子商務(wù)投訴與維權(quán)公共服務(wù)平臺(tái)檢測(cè)數(shù)據(jù)顯示的“2014年（上）十大網(wǎng)絡(luò)熱點(diǎn)投訴問題”中退換貨物問題所占比例為10%.隨著《新消費(fèi)者權(quán)益保護(hù)法》以及各大B2C電商“7日無(wú)理由退貨”策略的實(shí)施，消費(fèi)者的退貨意識(shí)正在逐漸增強(qiáng).調(diào)查顯示若對(duì)退換貨服務(wù)感到滿意，約40%的顧客愿意再次從同一電商購(gòu)物.約30%的潛在顧客愿意選擇有良好退換貨策略的電商.此外，高達(dá)約80%的顧客對(duì)網(wǎng)購(gòu)產(chǎn)品的退貨表示不信任［1］.這些都意味著退貨逆向物流對(duì)電商經(jīng)營(yíng)效益的影響至關(guān)重要，提高退貨物流配送水平刻不容緩［2］.

退貨屬于逆向物流的范疇.Fleischmann等［3］在1997年將逆向物流的研究細(xì)分為3個(gè)主要方面：逆向配送、庫(kù)存控制和產(chǎn)品規(guī)劃.國(guó)內(nèi)外學(xué)者對(duì)退貨逆向物流的研究較少且大部分文獻(xiàn)主要集中在退貨策略、運(yùn)作模式和逆向配送問題上［4-5］.其中，詹蓉等［6］提出集中式退貨中心比較適合B2C電商環(huán)境的逆向物流運(yùn)作模式，將現(xiàn)有紛繁雜亂的退貨先進(jìn)行匯總，再分類轉(zhuǎn)運(yùn)至相應(yīng)電商.在此模式下，退貨可以進(jìn)行統(tǒng)一管理，形成規(guī)模經(jīng)濟(jì)，降低退貨成本，退貨效率高，貨物的失蹤、錯(cuò)配情況也能得到良好的控制.

B2C電商環(huán)境下集中式退貨中心的物流配送系統(tǒng)是一個(gè)離散時(shí)間的動(dòng)態(tài)系統(tǒng)，良好的車輛調(diào)度規(guī)劃能夠很大程度上提高退貨中心的運(yùn)作效率.目前尚未存在針對(duì)退貨中心內(nèi)部的車輛調(diào)度研究，因此本文對(duì)該問題進(jìn)行研究和分析，以期提高退貨物流的運(yùn)作效率，并提升電商的經(jīng)營(yíng)效益.

1 問題描述

B2C電商環(huán)境下的集中式退貨中心的運(yùn)作模式與配送系統(tǒng)中的準(zhǔn)時(shí)策略——越庫(kù)一致，均在配送中心內(nèi)以一種有限的的暫時(shí)庫(kù)存或零庫(kù)存將產(chǎn)品從收貨點(diǎn)直接轉(zhuǎn)移到出貨點(diǎn)的內(nèi)部轉(zhuǎn)移形式，以減少庫(kù)存成本、加快貨物周轉(zhuǎn)速度為目標(biāo)［7］.Vanbelle等［8］提出符合越庫(kù)模式的基本布局與運(yùn)作流程（見圖1），該布局符合B2C電商集中式退貨中心運(yùn)作流程特性.

圖1 集中式退貨中心的基本布局與運(yùn)作流程Fig.1 Layout and operation process of concentrative reimbursement centre

電商退貨逆向物流最明顯的特點(diǎn)是退貨逆物流產(chǎn)生的時(shí)間、地點(diǎn)、品種以及數(shù)量等的不確定性，因而不能像控制正向物流一樣有計(jì)劃地管理逆向物流［6］.現(xiàn)有對(duì)越庫(kù)的研究都是基于需求驅(qū)動(dòng)的“拉動(dòng)”系統(tǒng)：貨物在到庫(kù)之前，其數(shù)量與目的地是已知的，即入庫(kù)車輛與出庫(kù)車輛的對(duì)應(yīng)關(guān)系已知.但是退貨逆物流的高度不確定性導(dǎo)致貨物在未到達(dá)退貨中心之前信息未知，它是供應(yīng)驅(qū)動(dòng)的“推動(dòng)”系統(tǒng)，因此集中式退貨中心的入庫(kù)與出庫(kù)車輛的對(duì)應(yīng)關(guān)系是未知的，這是該車輛調(diào)度問題的難點(diǎn)之一.

在車輛調(diào)度過程中，車與門的分配問題也是車輛調(diào)度問題的一部分.在有關(guān)越庫(kù)的研究中，多數(shù)學(xué)者將研究對(duì)象簡(jiǎn)化為單個(gè)出入門來(lái)研究車輛調(diào)度問題［9-11］，不存在車與門的分配問題，只考慮車輛排序問題.但是在電商環(huán)境下，退貨逆物流的特點(diǎn)決定退貨中心必定為多出入門，多出入庫(kù)車與門的分配問題極其復(fù)雜，部分學(xué)者在越庫(kù)研究中將該問題單獨(dú)提煉出來(lái)，將其看成獨(dú)立的調(diào)度問題進(jìn)行研究［12-13］，但是這不符合實(shí)際應(yīng)用情況.近些年有學(xué)者結(jié)合給定的車與門的分配策略的對(duì)車輛調(diào)度進(jìn)行研究，如Kuo［14］同時(shí)考慮車門分配和車輛排序問題，其優(yōu)化效果優(yōu)于單獨(dú)考慮車輛排序問題.

如圖1所示，入庫(kù)車i在給定入庫(kù)序列后，根據(jù)入庫(kù)車門分配策略分配入庫(kù)門c，在c處卸貨，退貨在中心完成分裝作業(yè)后裝載至由出庫(kù)車j并運(yùn)往對(duì)應(yīng)的電商.出庫(kù)車j根據(jù)出庫(kù)車門分配策略分配出庫(kù)門b.考慮到實(shí)際應(yīng)用中退貨中心的固定成本問題，出入庫(kù)門的數(shù)量必定遠(yuǎn)小于出入庫(kù)車輛數(shù)，因此在退貨中心出入庫(kù)門可以看作是稀缺資源，必須進(jìn)行相應(yīng)的調(diào)度［14］.該分配問題的復(fù)雜程度和難度與出入庫(kù)車輛和出入庫(kù)門的數(shù)量成正比［13］.考慮到本文研究對(duì)象中出入庫(kù)車輛到達(dá)時(shí)間和貨物種類與數(shù)量的不確定性，入庫(kù)車輛與入庫(kù)門的分配采取先到先服務(wù)的策略.由于該退貨中心是在B2C電商環(huán)境下，若投入實(shí)際應(yīng)用，應(yīng)確定電商數(shù)量遠(yuǎn)遠(yuǎn)小于客戶數(shù)量，本研究模型中每個(gè)出庫(kù)門指定對(duì)應(yīng)電商，為降低成本，出庫(kù)車數(shù)量一定，出庫(kù)車與出庫(kù)門的分配采取空缺補(bǔ)候的策略.

由于已有文獻(xiàn)中暫無(wú)適用模型，為了更清楚地闡述該問題并突出問題特性，作如下假設(shè).

1）針對(duì)退貨逆物流的特點(diǎn)，入庫(kù)車數(shù)量不確定、入庫(kù)車上所裝載的退貨種類和對(duì)應(yīng)的數(shù)量不確定.

2）考慮退貨中心成本問題，出庫(kù)車數(shù)量一定.當(dāng)現(xiàn)場(chǎng)暫無(wú)可用出庫(kù)車時(shí)，出庫(kù)門等待返程車，以等待先后順序分配返程的出庫(kù)車.

3）入庫(kù)車輛在初始時(shí)刻同時(shí)到達(dá)，出庫(kù)車輛在初始時(shí)刻均可用.

4）每輛出入庫(kù)車需分配一個(gè)且僅一個(gè)出入庫(kù)門.

5）入庫(kù)車在出入庫(kù)門的作業(yè)時(shí)間與貨物種類相關(guān)，一次只能卸載一個(gè)貨物且不能中斷.由于出庫(kù)門數(shù)量限制問題，為增加出庫(kù)效率，出庫(kù)門處一次能裝載5個(gè)貨物.

6）一輛車在進(jìn)行裝卸作業(yè)時(shí)不允許中斷插入其他車輛.

7）貨物在退貨中心內(nèi)部轉(zhuǎn)移時(shí)間與出、入庫(kù)門位置相關(guān).

8）貨物不允許暫存.

9）出庫(kù)車滿足最大載貨輛或最大發(fā)車時(shí)間必須發(fā)車.

根據(jù)該模型的需要，引入以下變量和常量.

入庫(kù)車：i∈I=｛1，2，…，m｝；

入庫(kù)門：c∈C=｛1 ，2 ，…，s｝；

出庫(kù)車：j∈J=｛1 ，2 ，…，n｝；

出庫(kù)門（貨物總類）：b∈B=｛1 ，2 ，…，l｝；

AIi：入庫(kù)車i進(jìn)入庫(kù)門的時(shí)間；

AJj：出庫(kù)車j進(jìn)出庫(kù)門的時(shí)間；

χib：入庫(kù)車i上電商b的退貨數(shù)量；

Pb：電商b單位貨物在出入庫(kù)門的裝卸時(shí)間；

T cb：貨物從入庫(kù)門c到出庫(kù)門b的轉(zhuǎn)運(yùn)時(shí)間；

FTc：入庫(kù)門c處的卸貨完成時(shí)間；

UTib：入庫(kù)車i上所有b類貨物卸貨完成時(shí)間；

LTib：入庫(kù)車i上的b類貨物在出庫(kù)門b處可開始裝載作業(yè)時(shí)間；

w b：出庫(kù)門b處理的貨物量；

TBbp：第p個(gè)b類貨物在入庫(kù)門處卸貨完成時(shí)間；

LTbp：第p個(gè)b類貨物到達(dá)出庫(kù)門b的時(shí)間；

FTbp：第p個(gè)b類貨物到達(dá)出庫(kù)門b處裝載完成時(shí)間；

ACb：出庫(kù)門b正在處理的出庫(kù)車上當(dāng)前累積貨量；

TLj：出庫(kù)車j的規(guī)定發(fā)車時(shí)間；

CC：出庫(kù)車滿載量；

t1：當(dāng)前無(wú)可用出庫(kù)車，貨物在出庫(kù)門的等待時(shí)間；

t2：更換出庫(kù)車所需時(shí)間；

貨物在退貨中心流轉(zhuǎn)時(shí)間的長(zhǎng)短是衡量退貨中心運(yùn)作效率的關(guān)鍵因素.因此以最小化所有貨物在退貨中心滯留的最大時(shí)間Tmax為目標(biāo)，結(jié)合第1章提出的9個(gè)條件并同時(shí)考慮出入庫(kù)車門分配問題建立數(shù)學(xué)模型.因?yàn)門max的計(jì)算與出入庫(kù)車門分配策略相關(guān)，計(jì)算復(fù)雜，無(wú)法用簡(jiǎn)單的數(shù)學(xué)語(yǔ)言進(jìn)行描述，所以在下文中提出一種入庫(kù)車與門的分配模型，并根據(jù)此模型給出最大完工時(shí)間計(jì)算模型.

2 出入庫(kù)車門分配模型與最大完工時(shí)間計(jì)算模型

出入庫(kù)車門分配模型可以看作2個(gè)階段，因此Tmax計(jì)算也可以分為2個(gè)階段.第1階段如圖2所示，入庫(kù)車根據(jù)先到先服務(wù)的策略分配入庫(kù)門，該模型會(huì)計(jì)算所有入庫(kù)車輛的卸貨完成時(shí)間.

當(dāng)入庫(kù)車輛數(shù)量m大于入庫(kù)門數(shù)量s時(shí)，假設(shè)前s輛入庫(kù)車在0時(shí)刻到達(dá)，入庫(kù)車分配到與它們具有相同序列號(hào)的入庫(kù)門處.當(dāng)i≤m時(shí)，AIi=0，對(duì)于所有的i=c來(lái)說，ICic=1.每輛入庫(kù)車的總卸貨時(shí)間取決于車上貨物的種類和數(shù)量.在模型中，卸貨作業(yè)每次只針對(duì)同一種類的貨物，只有當(dāng)同一種類的貨物都卸貨完畢后，才能被轉(zhuǎn)運(yùn)到相應(yīng)的出庫(kù)門，具體詳見圖2.當(dāng)i≥m時(shí)，該入庫(kù)車需要在入口處等待，所有等待的入庫(kù)車按照等待的先后次序依次分配到空閑的入庫(kù)門，具體的過程詳見如圖2所示的計(jì)算模型.

在第1階段入庫(kù)車門分配模型計(jì)算完所有入庫(kù)車輛的卸貨完成時(shí)間后，圖3中第2階段出庫(kù)車門分配模型會(huì)計(jì)算所有貨物的完工時(shí)間FTbp.當(dāng)某輛入庫(kù)車上某一類貨物全部卸載完畢后，該類貨物開始轉(zhuǎn)運(yùn)到對(duì)應(yīng)的出庫(kù)門b處，到達(dá)時(shí)間為L(zhǎng)Tbp.該出庫(kù)門b開始計(jì)算當(dāng)前出庫(kù)車j上的累積貨量ACb，判斷貨物到達(dá)時(shí)間是否超過當(dāng)前出庫(kù)車的發(fā)車時(shí)間TLj或當(dāng)前車輛貨物累積量ACb是否超過滿載量CC.若滿足其中任一條件則需等待下一輛出庫(kù)車j+1，等待時(shí)間為出庫(kù)車更換時(shí)間t2.因?yàn)槌鰩?kù)車數(shù)量有限，模型還須判斷現(xiàn)場(chǎng)的n輛出庫(kù)車輛是否均已在途，若均在途，則等待時(shí)間還需再加上等待時(shí)間t1，所以貨物p在出庫(kù)門b處的完工時(shí)間FTbp=LTbp+Pb+t1+t2.該模型以此計(jì)算每個(gè)貨物的完工時(shí)間FTbp，其中最大值就是最大完工時(shí)間Tmax.從圖2和3所示的2階段Tmax計(jì)算模型中可以

得到貨物在該退貨中心滯留的Tmax計(jì)算模型：

當(dāng)給定入庫(kù)車進(jìn)入退貨中心的序列后，圖2和3所示的分配模型會(huì)為出入庫(kù)車分配對(duì)應(yīng)的門，同時(shí)計(jì)算相應(yīng)的最大完工時(shí)間，因此該模型可以結(jié)合遺傳算法或其他啟發(fā)式算法，在多出入門和多出入庫(kù)車的環(huán)境下優(yōu)化入庫(kù)車調(diào)度序列.

3 數(shù)值實(shí)驗(yàn)與分析

傳統(tǒng)優(yōu)化算法從單個(gè)初始值迭代求最優(yōu)解，容易誤入局部最優(yōu)解.遺傳算法從串集開始搜索，覆蓋面大，利于全局擇優(yōu)，本文采用遺傳算法求解最優(yōu)入庫(kù)車序列.

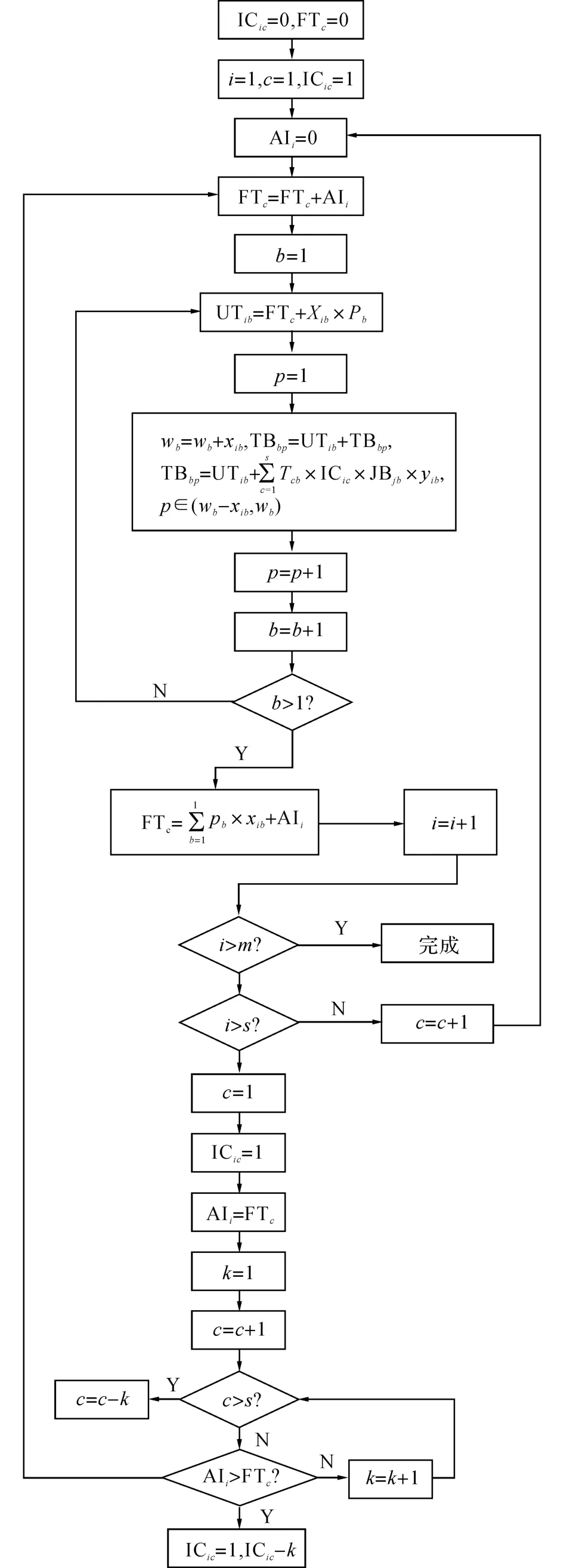
圖2 入庫(kù)車與入庫(kù)門的分配模型Fig.2 Inbound truck-door assignment model

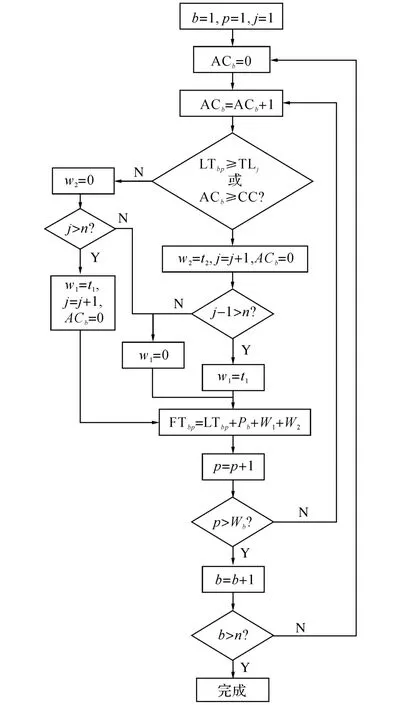
圖3 出庫(kù)車與出庫(kù)門的分配模型Fig.3 Outbound truck-door assignment model

從2階段計(jì)算模型中可以看出，最大完工時(shí)間Tmax受到某些變量的影響，包括出入庫(kù)車數(shù)量I、入庫(kù)門數(shù)量C、出庫(kù)車數(shù)量J、出庫(kù)門數(shù)量（貨物種類）B、從入庫(kù)車i轉(zhuǎn)移到出庫(kù)門b的貨物的數(shù)量X ib等.變量I和J決定了該退貨中心的處理量，變量C和B決定了該退貨中心的規(guī)模，而y ib決定了該問題的復(fù)雜程度.Kuo［14］提出，越庫(kù)的門數(shù)量范圍為6～200.如前文所述，每個(gè)出庫(kù)門指定對(duì)應(yīng)電商，因此出庫(kù)門與貨物種類，即電商數(shù)量一致，出庫(kù)門數(shù)量為5～20，入庫(kù)門數(shù)量為30～110.針對(duì)退貨逆物流的不確定性，X ib隨機(jī).實(shí)驗(yàn)規(guī)模如表1所示.I=C×z，J=C×z×5，其中z為調(diào)整出入庫(kù)車輛與入口數(shù)量關(guān)系的參數(shù)［13］.入庫(kù)車卸載的貨物種類以B×u為平均值隨機(jī)取值，因此u越大，從每輛入庫(kù)車上卸下的貨將被轉(zhuǎn)運(yùn)到更多的出庫(kù)門處，該問題的復(fù)雜度也就越大.

如表1所示，第8～10列分別為隨機(jī)解R，初始解IN和遺傳算法得出的最優(yōu)解，從改進(jìn)程度IM中可以看出，GA得出的解相對(duì)于隨機(jī)解均有一定的改進(jìn)程度，改進(jìn)程度為-0.79% ～37.49%.從圖4可以看出，在最初計(jì)算規(guī)模相對(duì)較小時(shí)，u=0.5和u=0.2的改進(jìn)程度差別不大，但當(dāng)計(jì)算規(guī)模逐漸增大，u=0.5時(shí)的改進(jìn)程度明顯低于u=0.2時(shí)，即當(dāng)入庫(kù)車上的貨物總類越多（或入庫(kù)車上的貨物準(zhǔn)備運(yùn)往的出庫(kù)車越多），本文提出的模型能夠改進(jìn)最大完工時(shí)間的程度變低.

由于問題的NP難特性，該調(diào)度問題的解空間會(huì)隨著u和出入庫(kù)車輛數(shù)的增大而大幅增加，計(jì)算時(shí)間也會(huì)因此增加.從圖5可以看出，隨著出入庫(kù)車量數(shù)的增加，求解時(shí)間t逐步增加，當(dāng)出入庫(kù)車輛數(shù)超過160時(shí)，t＞1 min，且當(dāng)u=0.5時(shí)求解時(shí)間長(zhǎng)于當(dāng)u=0.2時(shí)的求解時(shí)間.

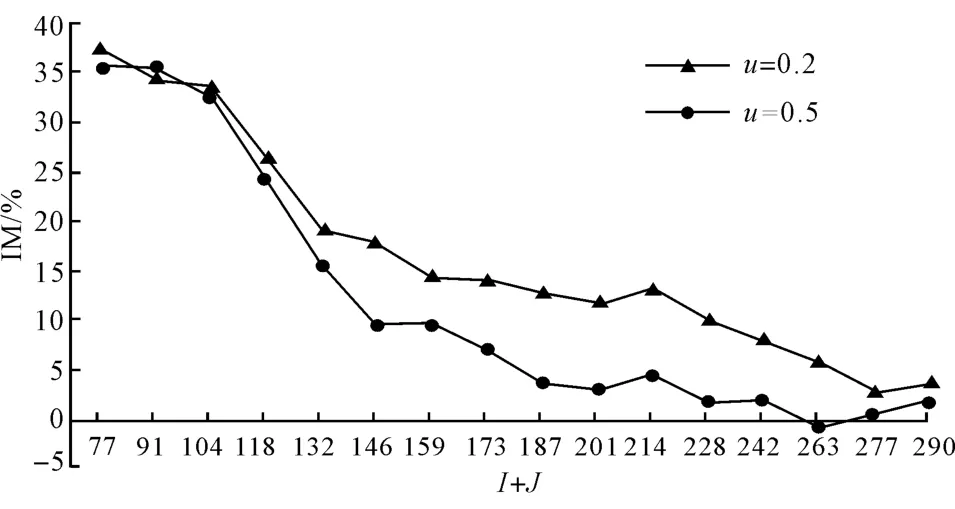
圖4 遺傳算法改進(jìn)百分比Fig.4 Improvement percentage by genetic algorithm

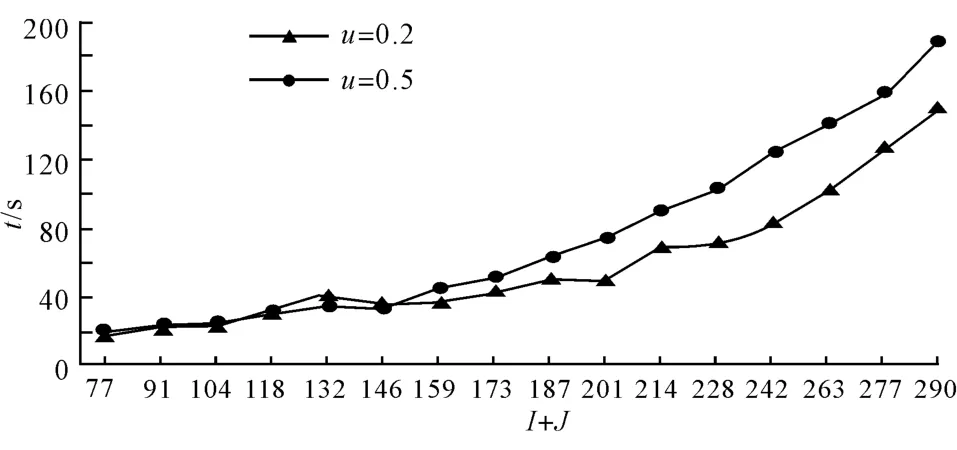
圖5 退貨中心規(guī)模和貨物種類對(duì)求解時(shí)間的影響Fig.5 Effect of reimbursement centre scale and types of goods on compouting time

4 結(jié) 語(yǔ)

本文模型能夠在一定程度上縮短最大完工時(shí)間，求解最優(yōu)入庫(kù)車序列.隨著配送中心規(guī)模的增大，求解速度變慢，且貨物種類越多，求解時(shí)間增長(zhǎng)速度越快.相對(duì)于隨機(jī)解，遺傳算法在一定程度上縮短了最大完工時(shí)間.與求解時(shí)間一樣，改進(jìn)程度受到配送中心規(guī)模和貨物種類的影響.此外，由于該車輛調(diào)度問題的高度復(fù)雜性，現(xiàn)階段只考慮了部分約束，進(jìn)一步地研究約束范圍是下一階段的研究目標(biāo).本研究所采用的車門分配策略比較簡(jiǎn)單，該問題有待深入研究.

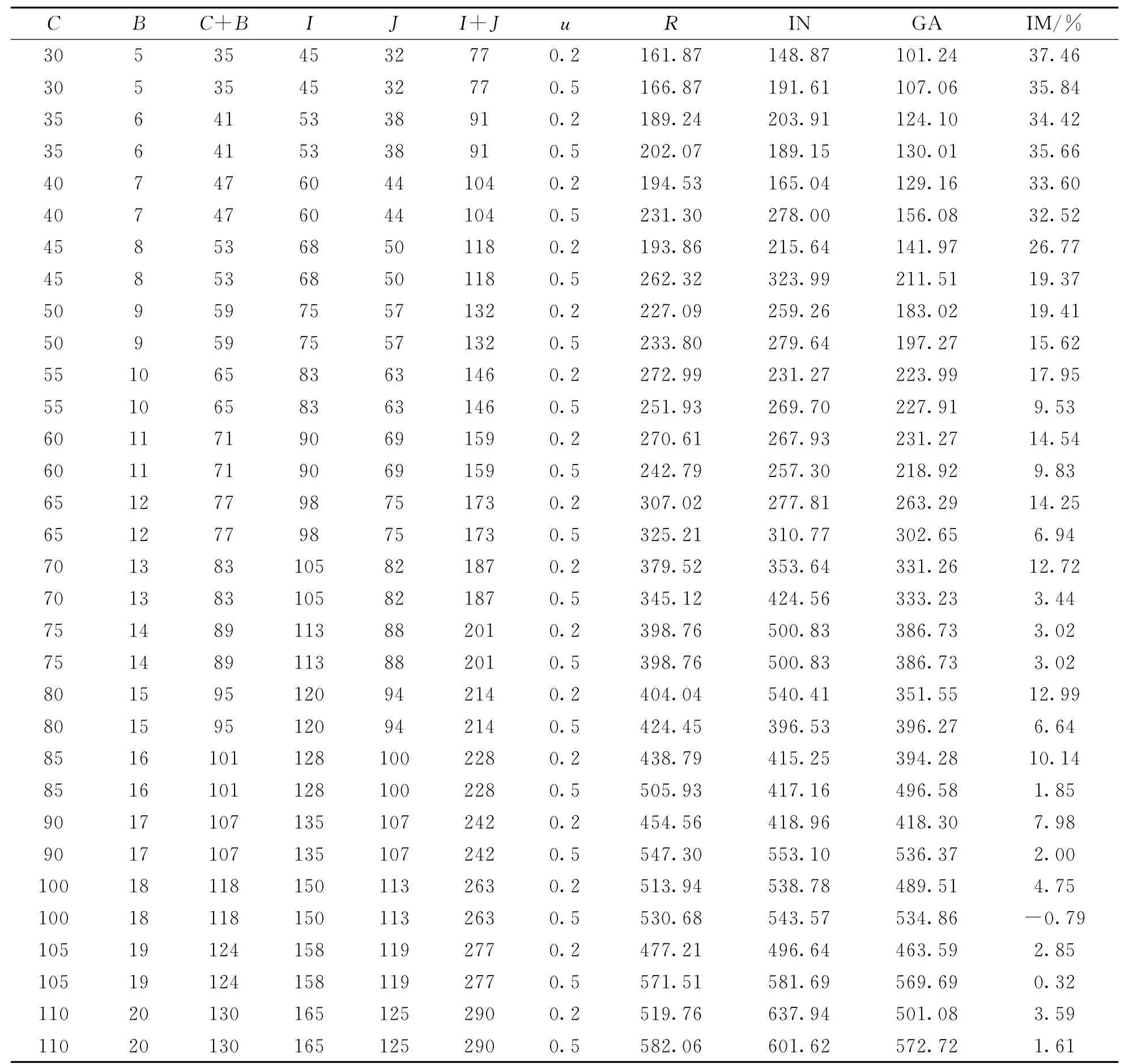
表1 實(shí)驗(yàn)設(shè)計(jì)與求解Tab.1 Design and calculation of experiment

（

）:

［1］WANG Z P，YAO D Q，HUANG P Q.A new locationinventory policy with reverse logistics applied to B2C e-markets of China［J］.International Journal of Production Economics，2007，107（2）：50- 363.

［2］許婷.我國(guó)B2C電子商務(wù)企業(yè)的物流配送模式研究及發(fā)展策略淺析［J］.現(xiàn)代商論，2014，22（3）：58- 60.XU Ting.Analysis and research on distribution strategy and development in B2C enterprises of China［J］.Modern Business，2014，22（3）：58- 60.

［3］FLEISCHMANN M，JACQUELINE M，BLOEMHOF R，et al.Quantitative models for reverse logistics：a review ［J］.European Journal of Operational Research，1997，103（1）：1- 17.

［4］郝建麗.網(wǎng)絡(luò)購(gòu)物中的退貨逆向物流研究［J］.現(xiàn)代營(yíng)銷，2011，5：1- 6.HAO Jian-li.Research on reverse Logistics of online shopping［J］.Modern Marketing，2011，5：1- 6.

［5］王妙春，汪貽生，姜玉宏.電子商務(wù)環(huán)境下逆向物流管理研究［J］.物流科技，2013（1）：115- 117.WANG Miao-chun， WANG Yi-sheng，JIANG Yuhong.Research on reverse logistics management based on E-business ［J］.Logistics Technology，2013 （1）：115- 117.

［6］詹蓉，陳榮秋.逆向物流運(yùn)作管理模型研究［J］.華中科技大學(xué)學(xué)報(bào)：自然科學(xué)版，2006，33（10）：115- 117.ZHAN Rong，CHEN Rong-qiu.Model for operations management of reverse logistics ［J］.Journal of Huazhong University of Science and Technology：Natural Sci-ence，2006，33（10）：115- 117.

［7］BOYSEN N，F(xiàn)LIEDNER M.Cross dock scheduling：classification，literature review and research agenda［J］.Omega，2010，38（6）：413- 22.

［8］VANBELLE J，VALCKENAERS P，CATTRYSSE D.Cross-docking：state of the art ［J］.Omega，2012，40（6）：827- 846.

［9］CHEN F，LEE C Y.Minimizing the makespan in a twomachine cross-docking flow shop problem ［J］.European Journal of Operational Research，2009，193（1）：59- 72.

［10］WOOYEON Y，EGBELU P J.Scheduling of inbound and outbound trucks in cross docking systems with temporary storage［J］.European Journal of Operational Research，2008，184（1）：377- 396.

［11］BOYSEN N，F(xiàn)LIEDNER M，SCHOLL A.Scheduling inbound and outbound trucks at cross docking terminals［J］.OR Spectrum，2010，32（1）：135- 161.

［12］MIAO Z W，LIM A，MA H.Truck dock assignment problem with operational time constraint within crossdocks［J］.European Journal of Operational Research，2009，192（1）：105- 115.

［13］BERMUDEZ R，COLE M H.A genetic algorithm approach to door assignments in breakbulk terminals［R］.USA，University of Arkansas：Mack-Blackwell National Rural Transportation Study Center，2001.

［14］KUO Y.Optimizing truck sequencing and truck dock assignment in a cross docking system ［J］.Expert Systems with Applications，2013，40（14）：5532- 5541.