基于遺傳優化的RBF-BP神經網絡電液伺服閥故障診斷算法研究

劉春艷， 樊立萍

(沈陽化工大學 信息工程學院， 遼寧 沈陽 110142)

基于遺傳優化的RBF-BP神經網絡電液伺服閥故障診斷算法研究

劉春艷， 樊立萍

(沈陽化工大學 信息工程學院， 遼寧 沈陽 110142)

電液伺服閥是液壓伺服系統的核心元件，因此是故障診斷的重點對象，其故障原因經常呈現出非線性和不確定性等復雜狀態.單一的BP網絡是全局逼近神經網絡，學習速度很慢，容易陷入局部極小，易產生震蕩等不足，RBF網絡是局部逼近神經網絡，訓練速度快，在訓練時不會發生震蕩，也不會陷入局部極小.基于它們各自的優缺點，通過將RBF神經網絡和BP神經網絡有效地結合在一起，取長補短，建立一個由RBF子網和一個BP子網兩部分串聯構成的雙隱藏層RBF-BP組合神經網絡.該網絡既具有BP網絡較好的泛化性能，又具備RBF網絡較快的逼近速度.用遺傳算法優化該神經網絡的初始權值和閾值.該網絡同時具有 RBF 網絡和 BP 網絡的優點，適用于復雜非線性系統的故障檢測.

故障診斷； RBF-BP神經網絡； 遺傳算法

電液伺服閥在液壓伺服系統中起著舉足輕重的作用.它的響應速度快，控制精度高，但由于其元件比較復雜，精密度高，且常在高溫高壓環境下工作，因此故障出現的頻率較高.而且一旦出現故障，不僅昂貴的診斷費用直接影響企業的經濟效益，還可能使整個工作線停止，嚴重時可能引起人員傷亡，造成嚴重的經濟損失，所以對電液伺服閥的故障進行有效診斷與維修具有重要的現實意義[1].

故障診斷技術發展至今，有智能故障專家系統、灰色系統理論、神經網絡理論、模糊理論等各種診斷方法.神經網絡具有很好的非線性函數逼近能力，結合電液伺服閥的特性，采用人工神經網絡對其進行故障診斷是一種有效的手段.BP網絡自學習、自適應能力強，但學習速度慢、易陷入局部最優，而RBF網絡具有學習快、能夠避免陷入局部最優等優點[2]，但對訓練樣本依賴性強，泛化能力較差.因此本文將兩種單一網絡相互結合構成一個雙隱藏層RBF-BP組合神經網絡對電液伺服閥進行故障診斷.

1 電液伺服閥的組成

電液伺服閥通常由力矩馬達(或力馬達)、液壓放大器、反饋機構(或平衡機構)三部分組成.如圖1所示.

圖1 電液伺服閥的組成原理

輸入信號由力矩馬達將電氣控制信號轉化為力矩或力來控制液壓放大器的運動；由液壓放大器控制液壓能源流向液壓執行機構的流量或壓力；反饋機構(平衡機構)的作用是將輸出流量或輸出壓力反饋到先導級閥的輸入端或比例放大器的輸入端，獲得所需的伺服閥壓力-流量性能，解決功率級主閥的定位問題[1].

電液伺服閥主要的失效形式有磨損(例如主閥芯控制窗口棱邊磨損和主閥套密封破損)、卡緊(如閥芯卡死或卡滯)、溫升等幾種.

2 RBF-BP組合神經網絡結構和參數設計

RBF-BP組合神經網絡是由一個RBF子網和一個BP子網兩部分組合而成的雙隱藏層神經網絡，第一隱藏層結點的傳遞函數使用高斯函數，第二隱藏層結點的傳遞函數使用Sigmoid型函數[3].

徑向基神經元模型[4]如圖2所示.

圖2 徑向基神經元

其徑向基傳輸函數為radbas,其輸出表達式為:

a=f(‖W-P‖·b)=

radbas(‖W-P‖·b),

(1)

(1)式也可表示為:

a(n)=radbas(n)=e-n2,

(2)

其中：

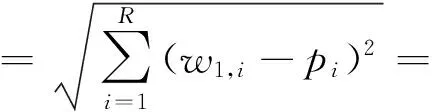
[(W-PT)(W-PT)T]1/2

(3)

BP神經元模型[5]如圖3所示.

圖3 BP神經元

若傳遞函數為tansig,其輸出表達式為:

a=f(Wp+b)=tansig(Wp+b);

(4)

(4)式也可表示為:

(5)

若傳遞函數為logsig,其輸出表達式為:

a=f(Wp+b)=logsig(Wp+b),

(6)

(6)式也可表示為:

(7)

RBF-BP組合神經網絡模型結構如圖4所示.其中P=(p1，p2…pi)T是輸入向量，pi是輸入向量的第i個元素，w1,j(i)是pi對應第一隱藏層第j個神經元的權值，(b11…b1j)T是第一隱藏層的閾值向量，w2,n(j)是第一隱藏層第j個神經元對應到第二隱藏層第n個神經元的權值，(b21…b2n)T是第二隱藏層的閾值向量，w3,k(n)是第二隱藏層第n個神經元對應到輸出層第k個神經元的權值，(b31…b3k)T是輸出層的閾值向量，Y=(y1，y2…yk)T是輸出向量.

圖4 RBF-BP組合神經網絡

3 算法描述

采用Delta(δ)學習規則，選擇均方誤差(mse)作為誤差準則函數，則有

(8)

式中:tk代表期望的輸出;yk為網絡的實際輸出;m為輸出層的神經元個數.

RBF-BP組合神經網絡的學習過程分為兩個步驟：

第一步是通過設置的網絡結構，學習樣本從網絡的第一層向后經過隱層處理，計算各神經元的輸出，傳向輸出層，這是正向傳播.

第二步是將誤差信號(理想輸出與實際輸出之差)按連接通路反向計算，從最后一層向前計算各權值和閾值對總差的影響(梯度)，據此不斷修正網絡的權值和閾值，這是反向傳播.

3.1 正向傳播

第一隱層第j個神經元的輸出pj采用radbas函數激發，由公式(1)、(2)、(3)得:

(9)

其中l為輸入層神經元個數.

第二隱層第n個神經元的輸入是第一隱層所有神經元輸出的加權和與閾值之和，即:

(10)

其中r為第一隱層神經元個數.根據公式(4)、(5)得第二隱層第n個神經元的輸出為:

(11)

輸出層第k個神經元的輸入是第二隱層所有神經元輸出的加權和與閾值之和，即:

(12)

其中s為第二隱層神經元個數.根據公式(6)、(7)得輸出層第k個神經元的輸出為:

(13)

網絡第k個輸出與相應理想輸出tk的誤差為:

ek=tk-yk,

(14)

根據公式(8)可知第p個樣本的誤差性能指標函數為:

(15)

3.2 反向傳播

采用SCG算法調整各層間的權值和閾值.在變梯度算法中，沿變化方向進行搜索，其收斂速度比最速下降法的速度更快.學習算法如下：

所有變梯度算法的第一次迭代都是沿著最陡梯度下降方向開始進行搜索[4]：

q0=-g0

(16)

然后決定最佳距離的線性搜索沿著當前搜索方向進行：

xh+1=xh+αhqh，

(17)

qh=-gh+βhqh-1,

(18)

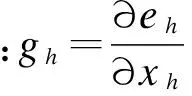
(19)

αh為搜索步長，由式mine(xh+1)決定，其結果為:

(20)

4 MATLAB實現

使用RBF-BP組合神經網絡進行故障診斷，首先設計網絡結構和輸入輸出模式，采用文獻[1]中的實驗數據，即在系統壓力分別為3、3.5、4、4.5和5MPa，5種狀態模式，16組固定電流下測得的進口壓差和出口壓差的實驗數據.因此網絡的輸出采用如下形式表示：

Y=(y1，y2，y3，y4，y5);

正常狀態： (1，0，0，0，0);

閥芯一端限位： (0，1，0，0，0);

一側固定節流孔堵塞： (0，0，1，0，0);

閥芯磨損： (0，0，0，1，0);

伺服閥零位不對中： (0，0，0，0，1).

因此RBF-BF組合神經網絡結構采取的是32個輸入、5個輸出、2個隱層數的神經網絡，隱層神經元的數目與輸入層神經元的個數有近似關系[11]：r=2×l+1，因此2個隱藏層的神經元個數均取65，然后創建網絡并設置相應參數.調用newff函數創建雙隱藏層的BP神經網絡，將第一個隱藏層神經元的傳遞函數設置為高斯(Gauss)型函數radbas，并將第二個隱藏層和輸出層神經元的傳遞函數設置為Sigmoid型函數tansig和logsig，采用的訓練函數為trainscg并設置學習率、訓練次數等相關參數.

另外，因無法準確獲得網絡的結構及初始連接權值和閾值，這對網絡訓練的影響很大.而遺傳算法具有較強的魯棒性，可以搜索全局的最優解，所以在對RBF-BP網絡訓練時，采用與遺傳算法相結合的方式對網絡的權值和閾值進行優化，獲得最佳的初始權值和閾值，使優化后的神經網絡能夠更好地進行樣本診斷.

圖5是遺傳優化后得到的權值和閾值矩陣X的誤差進化曲線，最小誤差e=0.039 42.

圖5 誤差進化曲線

圖6和圖7分別為使用隨機權值和閾值、使用優化后的權值和閾值兩種情況下的訓練誤差曲線.表1是輸出的預測值、預測誤差和訓練誤差.表1中測試樣本預測結果Y的5行數據分別代表檢測出的5種故障狀態，依次為正常狀態；閥芯一端限位；一側固定節流孔堵塞；閥芯磨損；

伺服閥零位不對中.通過比較可以看出，優化初始權值和閾值后的測試樣本的誤差由0.391 63減少到0.039 42，訓練樣本的誤差由0.625 51減少到0.092 99.網絡的訓練和樣本的測試效果都得到了很大的改善.

圖6 隨機權值和閾值訓練誤差曲線

圖7 優化后的權值和閾值訓練誤差曲線

權值和閾值測試樣本預測結果Y測試樣本的仿真誤差訓練樣本的仿真誤差0.98970.00460.28550.00390.0044使用隨機權值和閾值0.00290.99070.00260.00550.01130.05200.00030.73790.03300.03640.391630.625510.00530.00400.01500.99610.09540.00620.00890.01540.00750.91160.97990.00510.00060.00000.0000使用優化后的權值和閾值0.00020.96130.00020.00270.00070.00310.00281.00000.00040.00000.039420.092990.00190.00000.00020.99890.00970.00080.00240.00240.00090.9887

5 結 論

通過大量的樣本訓練，使用RBF-BP組合神經網絡進行故障診斷，并采用遺傳算法進行優化，得到網絡的權值和閾值等參數，將測試樣本輸入到訓練好的網絡，驗證了網絡的正確性.且采用SCG算法能加快訓練速度，網絡訓練次數較少，識別準確度高，能較準確的診斷出故障點，能滿足系統要求.

[1] 李成.基于B-P神經網絡的電液伺服閥的故障診斷[D].武漢：武漢科技大學,2010:1-45.

[2] 李仿華,王愛平,姚麗娜,等.基于遺傳優化的 RBF-BP 網絡的實時故障檢測[J].微型機與應用,2012,31(8):90.

[3] 諶愛文.基于BP和RBF神經網絡的數據預測方法研究[D].長沙:中南大學,2007:26-27.

[4] 周開利,康耀紅.神經網絡模型及其MATLAB仿真程序設計[M].北京:清華大學出版社,2005:101.

[5] 朱凱,王正林.精通MATLAB神經網絡[M].北京:電子工業出版社,2010:193.

[6] 孫英廣.神經網絡在徑流預測模型研究中的應用及軟件實現[D].大連:大連理工大學,2005:32-34.

[7] 劉倩.城市軌道交通客流誘導系統的研究與實現[D].北京:北京交通大學,2009:34-36.

[8] 王卓宇.SCG算法優化調強放射治療計劃子野權重研究[D].廣州:第一軍醫大學,2006:11-21.

[9] 王兆麗,王力.一個簡單高效的動態手勢識別方法[J].計算機工程與應用,2002(19):74.

[10]許丹,孫志林,潘德爐.錢塘江河口鹽度的神經網絡模擬[J].浙江大學學報：理學版,2011,38(2):235-236.

[11]史峰,王輝,郁磊,等.MATLAB智能算法30個案例分析[M].北京:北京航空航天大學出版社,2011:29-30.

Fault Diagnosis Algorithm Research of Hydraulic Servo Valve Based on Genetic Optimization of RBF-BP Neural Network

LIU Chun-yan， FAN Li-ping

(Shenyang University of Chemical Technology， Shenyang 110142， China)

The servo valve as a core component of the hydraulic servo system is the focus of fault diagnosis,and the cause of the malfunction often exhibits complex state of uncertainty and nonlinear.Single BP network is a global approximation of neural networks with some shortcomings,such as learning speed is very slow,easy to fall into local minima,and easy to produce shock.RBF network is a local approximation neural network with training speed,and it will not produce shock or trap in local minima during training.Based on their respective advantages and disadvantages,by using RBF network and BP network effectively together,this paper complements each other,and builds double combinations of hidden layers RBF-BP neural network consisting of two parts series.The network not only has better generalization performance of BP network,but also had a faster approach speed of RBF network.Genetic algorithm is used to optimize the initial weights and thresholds of the neural network.The network also has advantages of RBF network and BP network for complex nonlinear system fault detection.

fault diagnosis； RBF-BP neural network； genetic algorithm

2013-11-04

國家科技支持計劃項目(2012BAF09B01)

劉春艷(1989-)，女，遼寧普蘭店人，碩士研究生在讀，主要從事軋機故障診斷等方面的研究.

樊立萍(1965-)，女，山東淄博人，博士，教授，主要從事復雜系統建模與控制等方面的教學與研究.

2095-2198(2015)01-0049-05

10.3969/j.issn.2095-2198.2015.01.011

TP273

A