質量豎向不均勻分布時剛重比公式的探討

陳偉偉

CHEN Weiwei

(溫州設計集團有限公司，浙江 溫州325000)

為控制高層建筑的整體穩定性和重力二階效應，我國《高層建筑混凝土結構技術規程(JGJ 3—2010)》(以下簡稱高規)對彎曲型和彎剪型高層的剛重比提出了要求，即式(1)和式(2)。

式中:EJd—一個主軸方向結構彈性等效抗側剛度;

Gi—各樓層的重力荷載設計值;

H—結構總高度;

n—樓層數。

當滿足式(1)時，認為結構按彈性剛度計算的P-Δ 效應內力、位移的增量控制在5% 左右，如考慮實際剛度50% 的折減，則內力增量控制在10% 以內。重力二階效應的影響相對較小，可忽略不計。當滿足式(2)而不滿足式(1)時，則按彈性剛度計算的P-Δ 效應內力、位移的增量控制在5%～10%，考慮實際剛度的折減，則內力增量約為10%～20%［1-2］。

高層建筑混凝土結構總體上可視為長細比3～9 的懸臂桿，由文獻［2］可知，公式(1)、(2)建立在質量沿樓層均勻分布的基礎上，即各樓層質量和層高均相等。而實際工程絕大多數不滿足該假定。本文對質量沿豎向分布不均勻時的剛重比公式作一些探討和改進，得出一些可供參考的結論。

1 控制二階效應的剛重比限值

高層建筑混凝土結構穩定計算的力學模型簡化為沿高度受多個集中荷載的中等長細比的懸臂柱，其精確解析解的獲得是非常困難的。比較實用的方法是采用某種等效方法將不同位置的軸向荷載換算為懸臂柱頂部的荷載，進而求得臨界荷載的近似值［3］。文獻［3］介紹了懸臂柱受單個軸向荷載作用時，分別按臨界荷載比值關系換算(由蘇聯學者卡羅波夫提出［3］，以下簡稱“卡氏法”)和按側向位移相等換算(以下簡稱“側移等效方法”)得出的懸臂柱頂部等效荷載。

1.1 考慮質量豎向不均勻分布時的剛重比公式的推導

高H 的懸臂柱，柱頂受單個集中荷載PH(圖1)，其歐拉臨界荷載PHcr為:

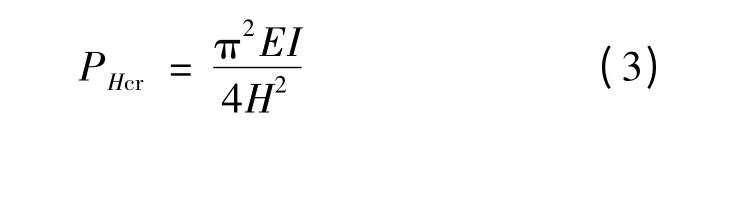
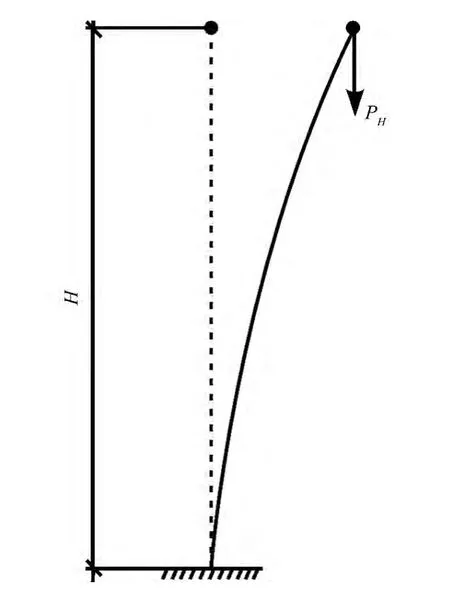
圖1 懸臂柱受單個集中力

圖2 懸臂柱受多個集中力

作為一種近似，當懸臂柱受多個集中力時(圖2)，將所有Pi乘以換算折減系數βi后移到柱頂，則總的柱頂等效荷載近似為令

即β 為總的換算折減系數，則

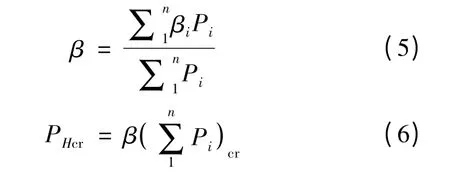
由式(3)、(6)可得，

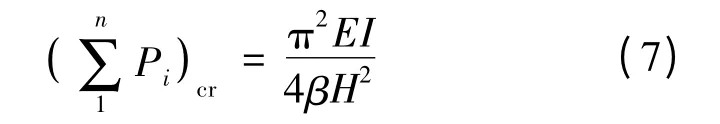
令

則式(9)即為以EI/H2為單位的的臨界荷載。由文獻［2］可知，考慮P-Δ 效應后的位移

式中Δ*和Δ 分別為考慮P-Δ 效應和不考慮P-Δ 效應的結構側向位移;

將式(9)代入式(10)，可得

按文獻［2］，當考慮P-Δ 效應后控制彈性位移放大系數為C1，即Δ*≤C1Δ;

將式(8)代入式(14)得，

當考慮P-Δ 效應后控制彈性位移增量在5%(C1= 1.05)或10%(C1= 1.10)以內時，有

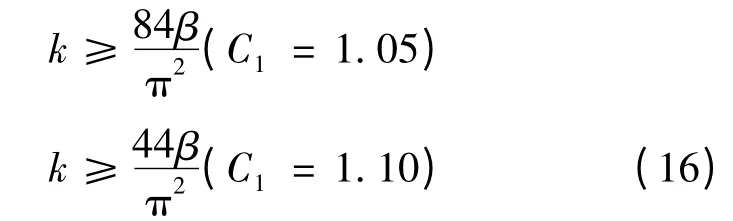
式(15)、(16)即考慮質量沿豎向不均勻分布時的剛重比限值計算公式。通過計算結構的總重量質量分布β 及等效側向剛度EJd就可以計算出剛重比及其限值，從而得到關于P-Δ 效應的判斷，這就是規范的思路。可以看出，剛重比限值直接與換算折減系數β 成正比。

1.2 β 值的計算

對卡氏方法［3］，

對側移等效方法［3］，

其中，

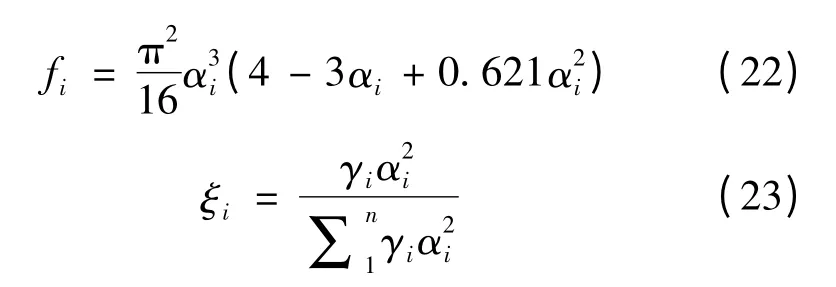
β 考慮了質量沿豎向的分布情況。對質量沿樓層均勻分布的高層建筑，當采用卡氏等效法時，

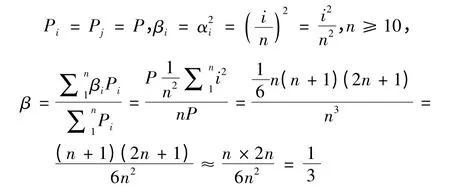
將β = 1/3 代入式(15)、(16)，可得:k ≥1.486(彈性位移增量≤10%)和k ≥2.837(彈性位移增量≤5%)。

按側移等效方法可以得到β = 0.314，代入式(15)、(16)可得:k ≥1.400(彈性位移增量≤10%)和k ≥2.672(彈性位移增量≤5%)。

此即高規公式(1)、(2)，高規取k ≥1.4(或2.7)。

但是當質量沿樓層分布不均勻時，β 的值將與1/3 或0.314 相差較大。在某些情況下，若仍采用式(1)、(2)判斷P-Δ 效應的影響范圍，將使設計偏于不安全。下面以兩個算例加以說明。

2 算例

2.1 算例一

一棟20 層的建筑(理想化為受20 個集中力的等截面均質懸臂柱)，質量分布上小下大，假設成1.05 的等差數列，則由卡氏方法、側移等效方法分別計算其臨界荷載，并給出有限元特征值屈曲分析結果作為對比(表1)，側移等效方法部分細節見表2。

注:(1)有限元特征值屈曲分析的β 是根據臨界荷載系數反算的，為保證計算精度，每個柱單元細分為三段［5］;(2)臨界荷載系數× 即為表2、表4 中臨界荷載因子P;(3)誤差均相對有限元解而言。下同。

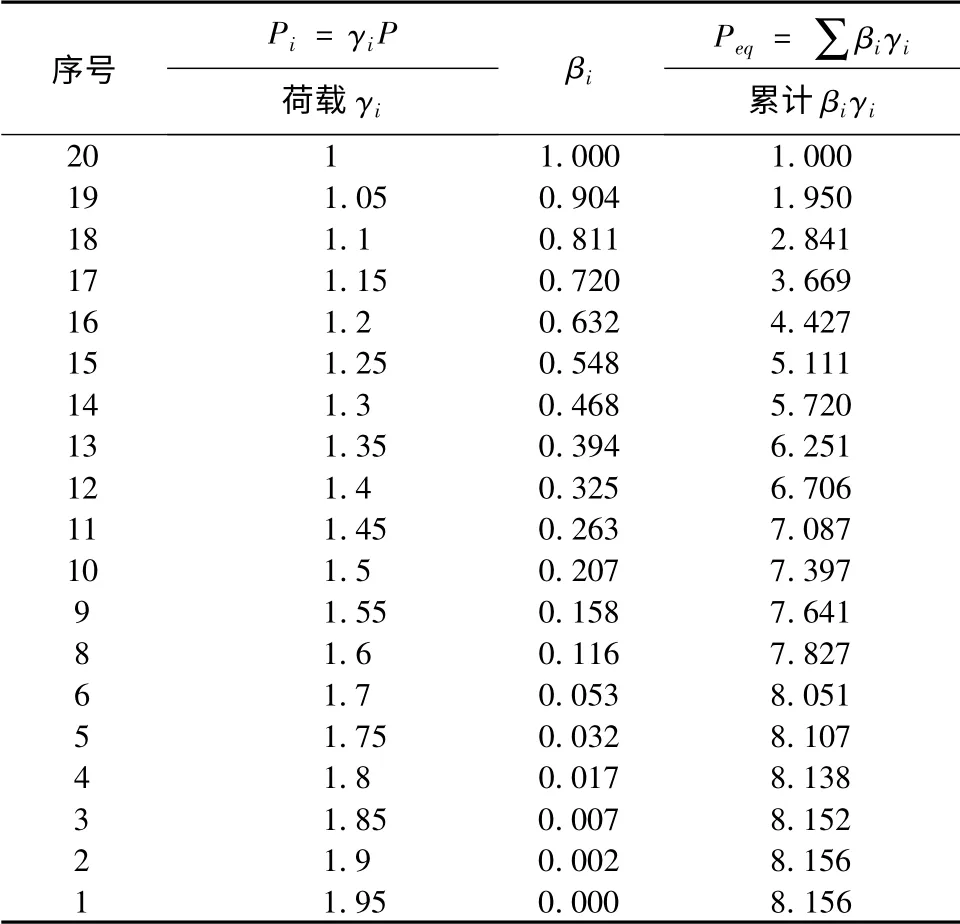
表2 側移等效法例1 臨界荷載系數計算細節

2.2 算例二

仍是一幢20 層的建筑，質量分布上大下小，假設質量比為1.05 的等差數列，則計算結果見表3，卡氏方法和側移等效方法部分細節見表4。

表3 例2 計算結果對比

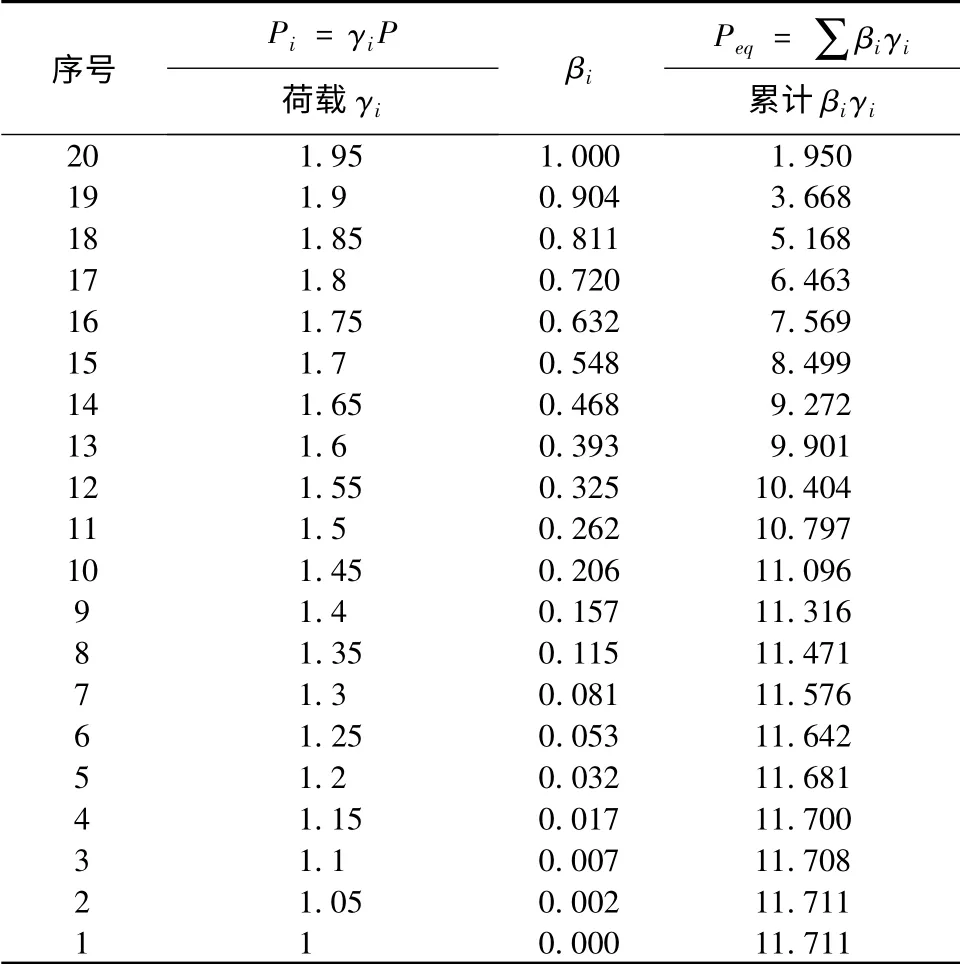
表4 側移等效法例2 臨界荷載系數計算細節

2.3 算例三

等截面直桿在自重作用下的臨界荷載見圖3。

圖3 自重作用下的等截面懸臂桿

精確解［6］:

由側移等效方法的推導如下:

由式(18)、(23)，可知

對式(26)積分并代入邊界條件ξ(0)=0 可得，

將式(27)代入式(21)可得:

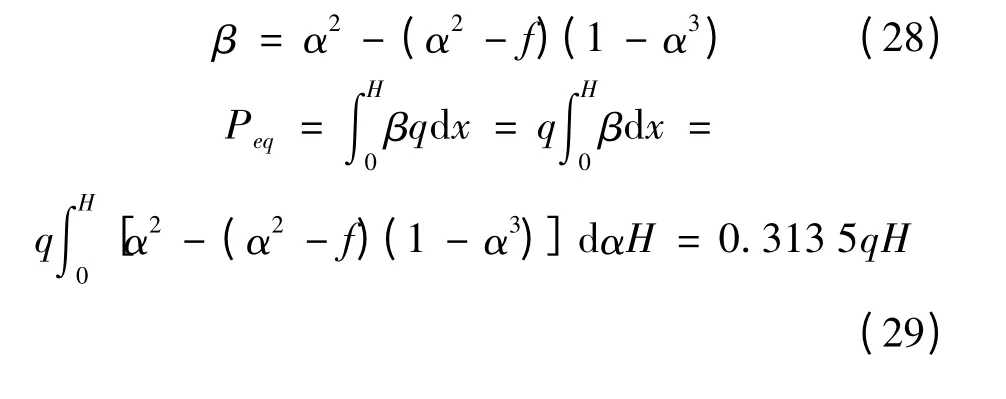
即β = 0.3135，將β 值代入式(8)、(9)可得:

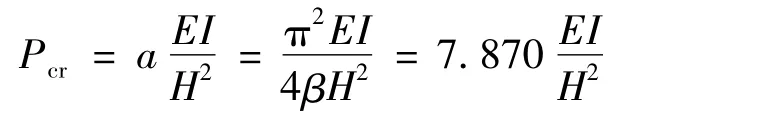
結果對比見表5。

表5 計算結果對比

由表1、表3 可見，對于質量分布為上小下大的結構(金字塔型，如上海中心［4］)，其臨界荷載系數較高，而換算折減系數β 較小(小于0.314)。對于質量分布為上大下小的結構(倒金字塔型)，其臨界荷載系數較小，換算折減系數β 較大(大于0.314)，若仍采用式(1)、(2)判斷P-Δ 效應的影響范圍則偏于不安全。由表1～5 可見，卡氏方法在質量均勻分布時，誤差為5.58%，當質量集中在上部樓層時誤差小于該值，當質量集中在下部樓層時，誤差大于該值;而側移等效方法則具有相對較高的精度(均是與有限元屈曲分析結果比較，基本均在5% 以內)，并且實際工程一般情況下質量集中在下部，也就是卡氏方法的誤差總是大于5.58% 的，所以推薦使用側移等效方法。

3 特征值屈曲穩定系數與剛重比

將式(3)代入，可得

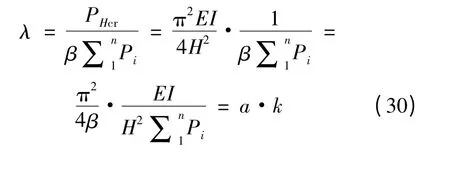
代入式(10)、(12)可得

由式(31)、(32)可見，λ 與二階效應位移放大系數直接相關，是控制二階P-Δ 效應更直接的參數(由文獻［2］知其對側向變形為剪切型的結構也是成立的)。

上海中心在1.0 恒載+1.0 活載下的第1、2 階屈曲系數為14.35 和14.79［4］，其在1.2 恒載+ 0.6活載下的屈曲系數近似估算(根據恒載活載比例按總荷載相等近似)為12.96 和13.35，代入式(31)，其二階效應放大系數為1.084 和1.081，即位移增幅約為8.0%，與其計算符合。

由特征值屈曲穩定系數λ 可以反算剛重比進行復核。由式(30)可以得到

對于實際工程，可以通過特征值屈曲分析得到穩定系數λ，再通過實際工程的Pi分布和Hi分布計算得到臨界荷載系數a 值，進而可以復核剛重比k。值得注意的是，由于高規規定的剛重比驗算重力荷載設計值采用了1.2 恒+ 1.4 活的組合，因此由式(33)復核剛重比，計算穩定系數λ 時，應采用同樣的重力荷載設計值。

對上海中心［4］而言，β = 0.25，代入式(8)得a = 9.870，1.2 恒載+1.4 活載下的屈曲系數近似估算(方法同前)為11.66 和12.02，代入式(33)得X 向 kx= 11.66/9.870 = 1.18，Y 向 ky=12.02/9.87 =1.22，

將β = 0.25 代入式(15)、(16)可得:k ≥1.115(彈性位移增量≤10%)和k ≥2.128(彈性位移增量≤5%)。

kx和ky均大于1.115，與原文結果符合。

4 結語

(1)通過對沿高度受多個集中荷載的中等長細比的懸臂柱臨界荷載的推導，引入質量分布換算折減系數β，對高規式(5.4.1 -1)和(5.4.4 -1)進行了推廣，即式(15)、(16)，使之適用范圍更廣;同時對β 值兩種計算方法的精度進行了對比分析，側移等效方法計算的β 值具有更高的精度。

(2)控制高層建筑線性P-Δ 二階效應更直接的參數是特征值屈曲穩定系數λ，λ ≥11 時，二階效應位移增量不大于10%，λ ≥21 時，二階效應位移增量不大于5%。由于高規規定的剛重比驗算重力荷載設計值采用了1.2 恒+1.4 活的組合，所以為復核剛重比及二階效應增量，而驗算特征值屈曲穩定系數時，應采用同樣的組合。特征值屈曲穩定系數λ 可以與剛重比互相校核。

［1]中國建筑科學研究院.JGJ 3—2010 高層建筑混凝土結構技術規程［S］.北京:中國建筑工業出版社，2010.

［2]徐培福，肖從真.高層建筑混凝土結構的穩定設計［J］.建筑結構，2001，31(8):69 -72.

［3]劉伯賢. 懸臂柱受多個軸向荷載作用時的穩定性及其設計［J］.中南公路工程，1987(2):49 -56.

［4]路天天，趙昕，丁潔民，等.上海中心大廈結構整體穩定性分析及巨型柱計算長度研究［J］. 建筑結構學報，2011，32(7):8 -14.

［5]江曉峰.有限單元法之梁柱單元的屈曲分析精度［J］. 結構工程師，2010，26(5):20 -25.

［6]陳驥.鋼結構穩定理論與設計［M］.5 版. 北京:科學出版社，2011.

［7]北京金土木軟件技術有限公司，中國建筑標準設計研究院.SAP2000 中文版使用指南［M］.北京:人民交通出版社，2006.