基于灰色理論的運城機場旅客吞吐量預測研究

邱 慧，解瑞金，劉二雄

(1. 運城學院 經濟管理系；2. 運城學院 應用數學系，山西 運城 044000)

基于灰色理論的運城機場旅客吞吐量預測研究

邱 慧1，解瑞金2，劉二雄2

(1. 運城學院 經濟管理系；2. 運城學院 應用數學系，山西 運城 044000)

通過選取2007～2014年運城機場旅客吞吐量的數據,對原始數據進行平均弱化緩沖處理，利用灰色GM(1,1)預測模型對運城機場旅客吞吐量進行預測，為運城機場擴建提供一些依據和數據支持，模型檢驗結果表明：均方差比值為一級,平均精度為一級,相對誤差等級為二級，預測模型可靠，精度較高。預測結果表明：到2018年的旅客吞吐量為1008548人次。

灰色系統理論；GM(1,1)；運城機場；旅客吞吐量

機場吞吐量的預測是機場乃至航空公司經營決策的基本前提,是實現機場資源有效配置的基本根據,其預測的準確度直接影響著機場改建、擴建的規模。就機場建設而言,機場吞吐量預測是機場項目建設可行性研究的一個重要課題。[1]它決定著項目是否可建以及建多大規模的問題,旅客吞吐量作為機場業務量的重要組成部分,其預測值已成為機場項目建設可行性研究的重要數據,同時決定機場建設規模的重要依據。目前已有許多學者對機場吞吐量預測進行研究，南娟等[2]運用巢式Logit模型對機場吞吐量進行預測，傅培華等[3]和陳玉寶等[4]運用組合預測模型分別對航空貨運吞吐量和民航旅客吞吐量進行預測，黃邦菊等[5]運用多元線性回歸分析的對民用運輸機場旅客吞吐量預測，其中有許多學者運用灰色理論對機場吞吐量進行預測研究。[6-11]

一、GM(1,1)模型[12-13]

GM(1,1)模型則是1階的，1個變量的微分方程模型,其適合于預測單變量的發展趨勢,即GM(1,1)模型是基于隨機的原始時間序列,經按時間累加后所形成的新的時間序列呈現的規律,可用一階線性微分方程的解來逼近。灰色預測充分考慮了未來變化對系統產生影響的各種不確定因素,能夠利用“少量數據”建模尋求現實規律的良好特性,克服了數據不足或系統周期短的矛盾,在這一點上優于統計和計量模型。

GM(1,1)模型建立的過程如下：

第一步:在構建傳統灰色GM(1,1)預測模型前,先對給定的數據列做事前檢驗。設原始數據為：

x(0)(1)，x(0)(2)，x(0)(3)…x(0)(n)

記

X(0)=(x(0)(1)，x(0)(2)，x(0)(3)…x(0)(n))

(1)

一般是用級比σ(0)(k)的大小與所屬區間來判斷。其級比為：

第二步:對原始數據X(0)做一次累加,累加后得：

X(1)=(x(1)(1)，x(1)(2)，x(1)(3)…x(1)(n))，

其中

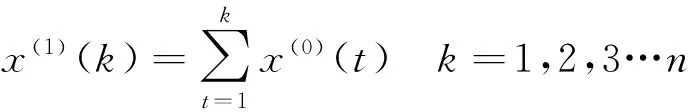
經過累加運算之后,原始數據的隨機性和波動性明顯被弱化了,隨之轉化成規律性較強的遞增數列,這也為建立微分方程形式的預測模型做好了充分的準備,使得應用過程更加簡化。

第三步:對生成序列

X(1)=(x(1)(1)，x(1)(2)，x(1)(3)…x(1)(n))，

建立一階線性微分方程模型

(2)

該微分方程就是灰色預測模型GM(1,1),上式中a,u為常數,由灰色理論知,系數向量ω=(a，u)T能夠通過最小二乘法擬合得到：

其中

Yn=(x(0)(2)，x(0)(3)，x(0)(4)…x(0)(n))T

則微分方程(2)的解：

(3)

則(3)式就是模型GM(1,1)的預測公式。

公式(3)是對原始數列一次累加生成數列的預測值,通過下式可以求出原始數列的還原預測值：

(4)

其中k=1，2，3…n-1。

1.2 緩沖算子

設原始數據序列

X(0)=(x(0)(1)，x(0)(2)，x(0)(3)…x(0)(n))

令

XD=(x(0)(1)d，x(0)(2)d，x(0)(3)d…x(0)(n)d)

其中

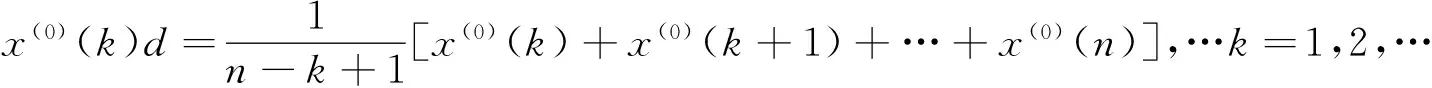
令XD2=XDD=(x(0)(1)d2，x(0)(2)d2，x(0)(3)d2…x(0)(n)d2),

則當X(0)為單調遞增、單調遞減或振蕩序列時,D為平均弱化緩沖算子，D2為二階平均弱化緩沖算子。

1.3 模型檢驗

相對誤差檢驗

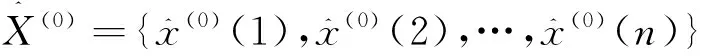
(5)

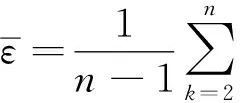
(6)

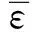
平均精度檢驗

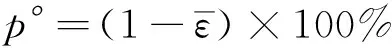
(7)

對于給定的p,當p>p°時,稱該模型為平均精度合格模型。

均方差比值檢驗

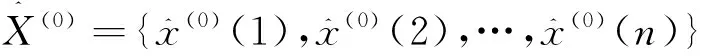
令

則

(8)

分別為X(0)的均值和方差;

(9)

分別為殘差的均值和方差。

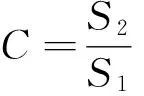
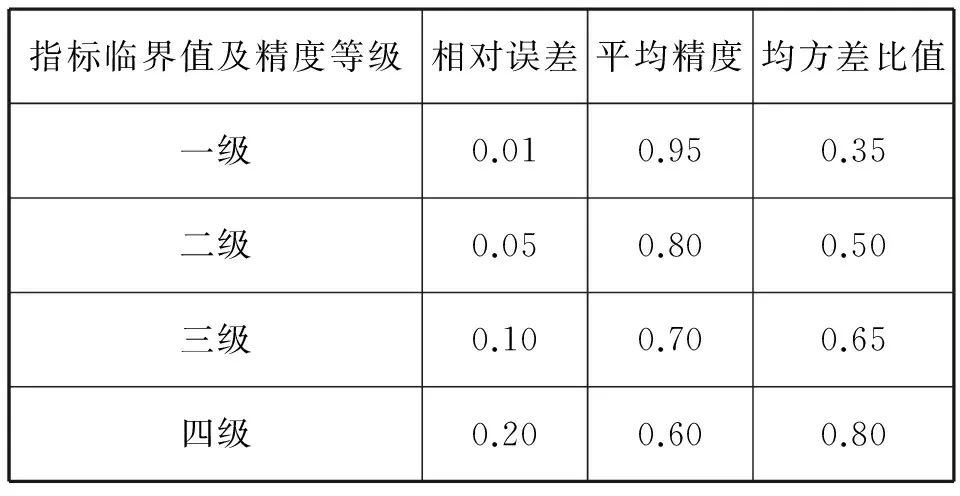
表1 精度檢驗等級參照表

二、模型應用

(一)運城機場簡介

運城關公機場(即運城機場)位于山西省西南部運城市,2005年,運城機場正式通航,這為游客到山西南部旅游提供了便利。運城機場的通航,結束了山西省南部沒有民用機場的歷史,填補了晉陜豫黃河金三角地區的空中交通空白,在國內民用機場排位由94名上升至2012年的60名，在山西排名第二。截止2013年12月31號，運城機場年旅客吞吐量達到1010070人次，首次突破100萬人大關。運城機場是運城的空中走廊，戰略意義十分重要。隨著運城市經濟的發展，必然會導致商務、公務、旅游等方面的人次增加。因此對運城(關公)機場業務量數據預測十分必要，對機場的建設和管理提供科學依據。

(二)GM(1，1)模型預測運城機場旅客吞吐量

在運城機場發展初期，機場旅客吞吐量基數少，有相當大的發展空間，所以增長速度很快。但是隨著近幾年運城經濟的增速的放緩，2014年運城全年全市生產總值降到比上年增長5.0%，導致現階段運城機場旅客吞吐量增長速度逐漸變得緩慢，甚至2014年出現負增長，比上一年減少7.3%，與運城機場發展初期的的增長速度不同，所以不能用以2007～2014年運城機場旅客吞吐量情況為原始數據進行建模，對原始數據進行平均弱化緩沖處理，才能更為精準的預測未來運城機場旅客吞吐量。

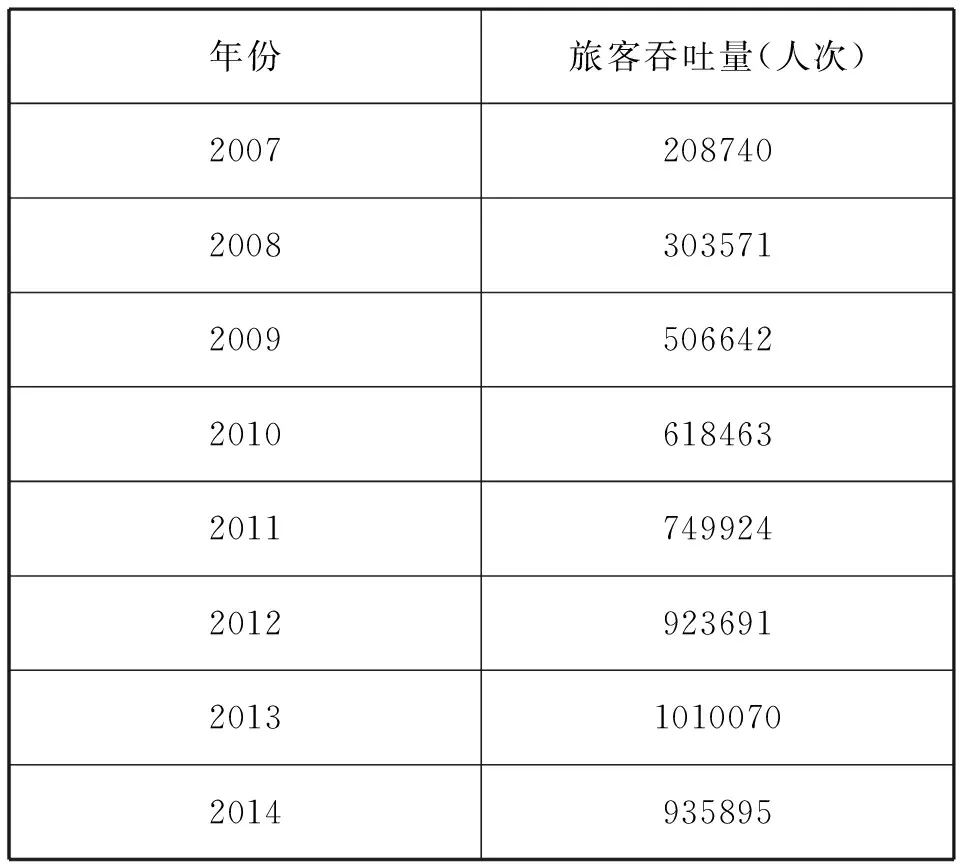
表2 2007～2013年運城機場旅客吞吐量情況

從表2中,可以得到原始數據：X(0)=(208740，303571，506642，618463，749924，923691，1010070，935895)，

對原始數據二階弱化處理，得二階平均弱化緩沖算子為：XD2=(848377，875699，901453，923587，942581，955143，954439，935895)。

接下來我們開始構建GM(1,1)模型:

第一步,級比檢驗。

(1)求級比，

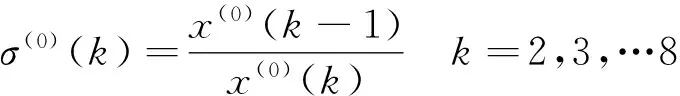
σ(0)=(σ(0)(2)，σ(0)(3)，σ(0)(4)…σ(0)(8)) =(0.9688，0.9714，0.9760，0.9798,0.9868,1.0007,1.0198)

(2)級比判斷。

由于所有的σ(0)(t)∈(0.8007,1.2488)t=2,3…8,所以可以作GM(1,1)模型。

第二步,GM(1,1)建模。

(1)對原始數據做一次累加,即

X(0)=(848377，1724076，2625529，3549116，4491697，5446840，3401279，7337174)

(2)構造數據矩陣B即數據向量Yn,即

及Yn=(875699,901453,923587,942581,955143,954439,

935895)T

(3)計算ω,即

于是得到a=-0.0121,u=878032.3827

(4)建立模型,

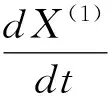
求得解

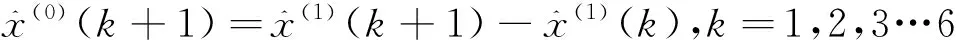
第三步,對模型進行檢驗。

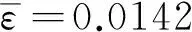
平均精度為p°=98.58%

S1=36345，S2=8162

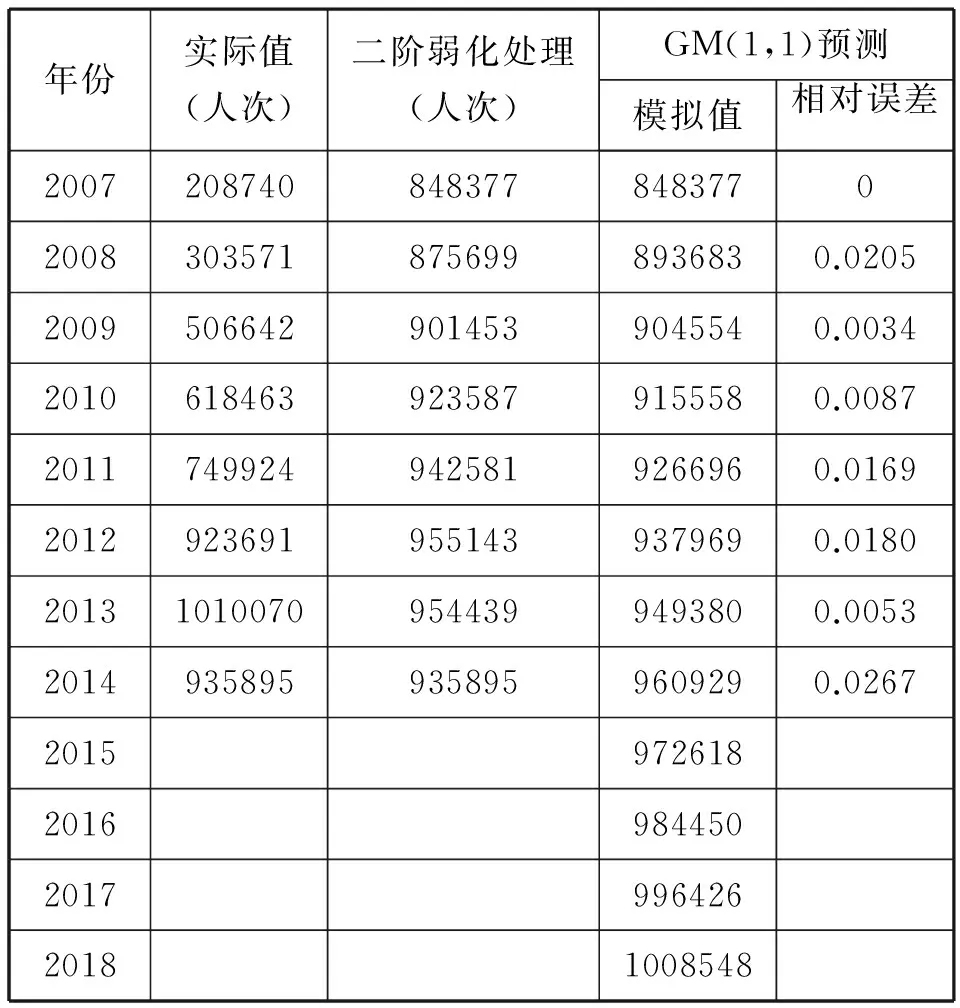
表3 2007～2018年運城機場旅客吞吐量的預測結果

GM(1，1)模型對2015-2018年運城機場旅客吞吐量預測為：972618人次，984450人次，996426人次，1008548人次。預測結果表明：到2018年的旅客吞吐量重返百萬。模型檢驗結果表明：均方差比值為一級,平均精度為一級,相對誤差等級為二級，預測模型可靠，精度較高。

三、結語

模型優點：灰色GM(1,1)預測模型在工業、農業、商業等經濟領域,以及環境、社會和軍事等領域中都有廣泛的應用，并且灰色預測主要通過對“小樣本”、“貧信息”的生成、挖掘、提取、利用有價值的信息,實現對系統行為、變化規律的正確描述和有效監控。灰色預測的主要特點是建立預測模型需要的原始數據不多，而且原始數據很容易采集，另外，這種預測方法簡便并具有較高的精度。模型缺點：由于GM(1,1)模型的應用和研究對象在多數情況下是復雜系統,它的內部包含大量內隨機性、線性、非線性等諸多因素,而且外部環境經常多變,很容易受到其他因素的干擾,從而增加了對掌握這些系統內部變化規律細節的難度，一般適合做短期或中長期預測。

機場旅客吞吐量的預測對機場的建設與管理具有重要意義。由于運城機場是通航時間不足十年，機場旅客吞吐量的歷史數據較少，而灰色GM(1,1)預測模型的主要特點是建立預測模型所需要的原始數據不多,這種預測方法簡便并具有較高的準確性。本文通過選取2007～2014年運城機場旅客吞吐量的數據，對數據進行分析,發現2014年的數據出現負增長，比上一年減少7.3%，與運城機場發展初期的的增長速度不同，所以利用二階平均弱化緩沖算子，對原始數據進行平均弱化緩沖處理之后，再通過建立GM(1,1)模型，對運城機場未來的旅客吞吐量進行了預測，得到較合理，精度較高的預測結果，有較高的可信度，為有關部門和領導決策提供了科學依據。然而，影響機場旅客吞吐量的因素很多，特別是現代區域經濟系統均為開放系統，加之氣候條件的變化﹑人為政策等不確定因素，經濟發展就會出現周期性的波動，為了避免機場旅客吞吐量預測結果與實際有較大的出入，只對2015-2018年運城機場旅客吞吐量做了短期預測。

[1] 林小平,袁捷.基于灰色模型的成都雙流機場物流預測[J].武漢理工大學學報：交通科學與工程版，2007(3).

[2] 南娟,王結.基于巢式Logit模型的機場吞吐量預測方法[J].科學技術與工程,2008(8).

[3] 傅培華,鮑福光,李進.基于組合預測模型的航空貨運吞吐量預測研究[J].上海管理科學,2012(2).

[4] 陳玉寶,曾剛.基于組合預測方法的民航旅客吞吐量預測研究-以首都機場為例[J].中國民航大學學報,2014(2).

[5] 黃邦菊,林俊松,鄭瀟雨,等.基于多元線性回歸分析的民用運輸機場旅客吞吐量預測[J].數學的實踐與認識,2013(2).

[6] 舒嚴嬌.機場旅客吞吐量預測方法研究[D].南京:南京航空航天大學,2008．

[7] 姚晏斌,高金華.灰色模型GM(1,2)在機場旅客吞吐量預測中的應用[J].中國民航飛行學院學報,2006(4).

[8] 徐勤蘭,樊重俊,張鵬.灰色支持向量機在機場吞吐量預測中的應用[J].上海理工大學學報,2012(4).

[9] 趙景麗，馬建新，吳興偉，等.基于GM(1,1)和BP網絡的港口吞吐量預測[J].大連交通大學學報,2013(3).

[10] 關靜.基于灰色支持向量機的民航旅客吞吐量預測[J].大連交通大學學報,2013(3).

[11] 董秀麗.環渤海地區機場旅客吞吐量分析與預測[J].中國民用航空，2014(2).

[12] 鄧聚龍．灰色預測與決策[M]．武漢:華中理工大學出版社,1992．

【責任編輯 楊 強】

2015-02-11

運城學院科研基金項目(YQ-2011080，SWSX-201304，XK-2014037，XK-2014039)

邱慧(1982-)，女，河北邢臺人，運城學院經濟管理系助教，碩士，研究方向為決策科學。

F22

A

1008-8008(2015)04-0033-04