基于局部和全局采樣點云數據簡化算法研究

付 瑋，吳祿慎，陳華偉

(1．南昌大學機電工程學院，江西 南昌330031;2．南昌航空大學航空制造工程學院，江西 南昌330069)

1 引言

目前，3D激光掃描技術［1－2］在快速、準確地獲取點云數據方面有了很大的進展，但是，如何處理這些龐大的點云數據成為基于3D激光掃描技術的主要問題。直接處理大量的點云數據，數據存儲和處理便成為難以突破的瓶頸。實際上，并非所有的點云數據對模型重建都有用處，因此，有必要在保證一定精度的前提下，對點云數據進行簡化處理。

一般點云簡化方法包括:基于曲率和基于空間分割兩大類方法。基于曲率方法有角度偏差法［3］、最小距離法［4］等;基于空間分割方法有均勻網格法［5］、包圍盒法［6］、基于三角網格方法［7］。兩類方法各有局限，基于曲率的簡化算法雖能很好地保留幾何特征，但是簡化效率低［8］;基于空間分割的簡化算法不適用于復雜特征和多曲率的散亂點云數據簡化［9］。

很多研究學者在數據簡化的研究中，提出了各種不同的處理方法，Vero和Leon［10］在1997年提出一種用誤差帶(Error Zones)減少多面體數據點的方法。Chen Y．H．［7］1999年提出一種通過減少網格模型中的三角形，從而達到減少數據點的方法。這種方法先直接將測得的數據轉換成STL文件，然后通過減少STL文件的三角形數量，以實現減少數據量。本文提出了一種有效的點云數據簡化方法，將局部和全局的采樣特征相融合。該方法既考慮了局部點云細節，又考慮了點云的全局形狀特征，可以有效的簡化點云數據。對形狀比較復雜的曲面(汽車模具等)有比較好的簡化效果。

2 局部點云特征采樣

本文采用基于點云的網格分割的非均勻網格法來提取局部點云特征。非均勻網格法［6］是點云簡化中較常用的方法之一，采用非均勻網格法可以去除大量的數據點。該方法可以采用角度偏差法從模型表面點云數據中獲取數據樣本。

角度可通過三個連續點的方向矢量計算得到，如圖1所示，(x1，y1)，(x2，y2)，(x3，y3)三點。角度代表曲率信息，角度大，曲率就大;反之，角度小，曲率也小。根據角度大小，高曲率的點可以被提取出來。通過角偏差抽取的點代表高曲率區域。為準確地表示零件外形，進行點云數據簡化時，必須保留這些點。這樣，使用角度偏移法進行點云提取后，對曲率小的區域采用大網格尺寸進行點云簡化，對曲率大的區域采用較小網格尺寸進行點云簡化。如圖2所示，分離過程中網絡尺寸大于最大網絡尺寸，網格被進一步分割，直到小于最大網格尺寸為止。當對網格中點應用中值濾波時，將產生一個代表樣點。最后，保留點是由每個網絡的中值濾波點和角度偏移提取的點組成向量L。通過非均勻網格法進行點云簡化，不但有減少點云數據的功能，還能有效去除噪聲點，另外，這種方法只是選用其中的某些點，并不改變點的空間位置，可以很好地保留原始數據。

圖1 角度偏差法

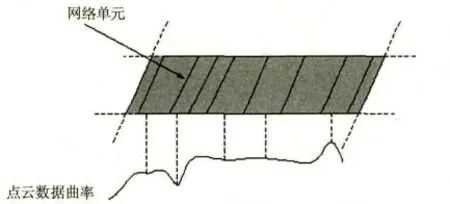
圖2 非均勻網格法簡化數據點

3 基于體素的全局點云特征采樣

本文提出一種基于空間體素化方法對點云進行全局采樣，可以最大限度地反映點云的全局特征。

體素是體圖形學中描述體模型的基本數據單元。體素化(Voxelization)是從面模型到體模型的轉換過程，其任務是:將物體的幾何形式表示離散成最接近該物體的體素表示形式，產生體數據集，表示模型的空間體素跟表示圖像的二維像素比較相似，可以理解為從二維的點擴展到三維的立方體單元。

對于數據量比較大的點云，它的點云分布一般是雜亂無章的，計算機處理這些點云數據時，非常耗費時間，效率比較低，不能達到實時處理的目的。因此，有必要將冗余點或者無用點去除，而體素化的方法，恰好可以解決這一難題，它可以大大地減少點云的數據量。

首先，使用規則的三維網格來劃分點云空間，每個點云都在三維立體單元中，其存儲了每個體素的質心坐標和點云數。體素化方法主要是針對點云的XYZ坐標值的編碼。編碼是采用12位的整數，它由3部分四位數組成。每部分表示其中一個XYZ坐標值，將其除以體素大小，便可將坐標值轉換為體素單元，并且用最小的XYZ坐標值來替代原始點云數。參見公式(1)。這樣，三部分就可以組成一個簡單的編碼。簡單的編碼原理如圖3所示。

編碼格式:

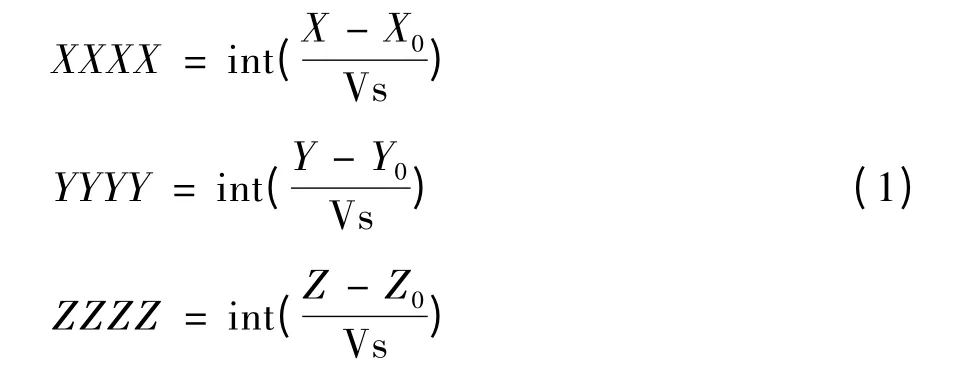
其中，X，Y，Z分別是體素的坐標值，X0，Y0，Z0分別是體素X，Y，Z坐標值的最小值;Vs是體素大小。

12位編碼值儲存在一個簡單向量G中。向量長度等于點云數N。考慮到屬于同一體素中的點云有相同的編碼，向量元素根據它們的數值大小來分類。因此，同一體素內的點被聚集在一起。如圖3所示。為了獲取更多的采樣點，體素單元網格需要進一步細分，如果體素單元網格的標準偏差大于給定值，則單元網格被繼續細分;這個過程反復進行直到網格的標準偏差小于給定值;或者網格尺寸達到用戶設定的值。通常網格最小尺寸根據零件復雜程度選定。

編碼算法過程:假設有一個點，其體素尺寸大小取為0．1 cm。其X坐標值為:2468．232;Y坐標值為:3578．556;Z坐標值為:98．662。其Xmin為:2000;Ymin為:3000;Zmin為:0;根據公式(1)得:X體素值為:4682;Y體素值為:5785;Z體素值為:986。最后，12位的編碼為:468257850986。表1是對12個體素點的編碼。

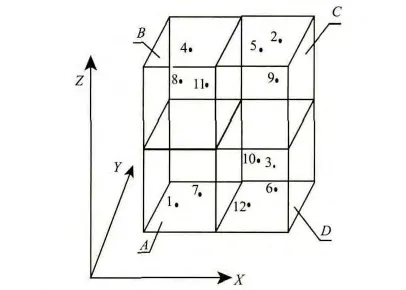
圖3 體素單元

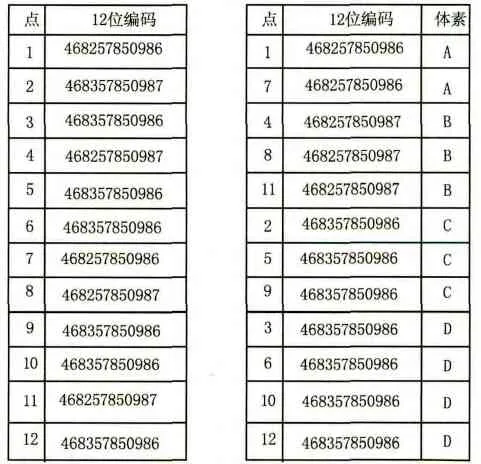
表1 點云索引及編碼

由表1可以看出，點1，7在A體素中;點4，8，11在B體素中;點2，5，9在C體素中;點3，6，10，12在D體素中。可以將點1，4，2，3(分別屬于體素A，B，C，D)組成一個向量G，由該矢量代表體素的特征值，其他的值可以濾去，這樣原來體素中有12個點，經過此方法后簡化為4個點。但是可以完全的表達點云的全局特征。

4 點云特征的融合

為了獲取更好的簡化結果，這里將局部和全局采樣點特征融合在一起。L是局部采樣特征值，G是全局采樣特征值，點云簡化特征S可以通過公式(2)來定義:

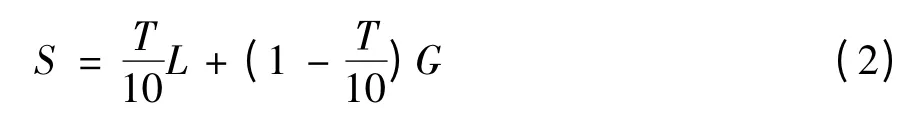
其中，T是控制局部采樣點集和全局采樣點集的權重。如果T過大，這種方法仍然可以很好地表示全局形狀，但它可能會失去許多局部的形狀細節。當T變小時，可以比較好地表示局部形狀，但全局形狀表示可能會受到影響。因此，需要通過實驗找到一個合適的T值。

5 實驗及誤差分析

5．1 算法實驗

圖4是利用該算法進行點云數據簡化的流程圖，首先通過三維光柵掃描、解相、去包裹、除噪等過程獲取物體三維點云圖。

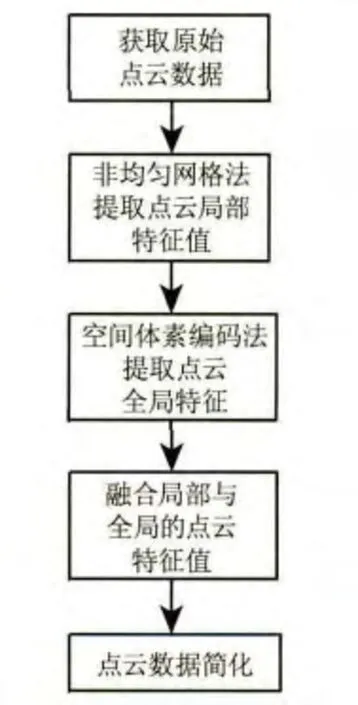
圖4 點云簡化算法流程

通過非均勻網格法提取點云數據曲率比較大的局部特征值;然后運用空間體素編碼法提取點云數據的全局形狀特征值。最后，使用公式(2)將二者特征值融合，獲取點云簡化最佳效果值。

為了驗證算法的有效性和正確性，本文分別對Bunny模型和某型號汽車模具點云進行簡化，如表2所示三種算法的點云簡化數據。測試環境為:Intel core 2．0 GHz，CPU 2G內存;根據實驗，權值取T=6．5。

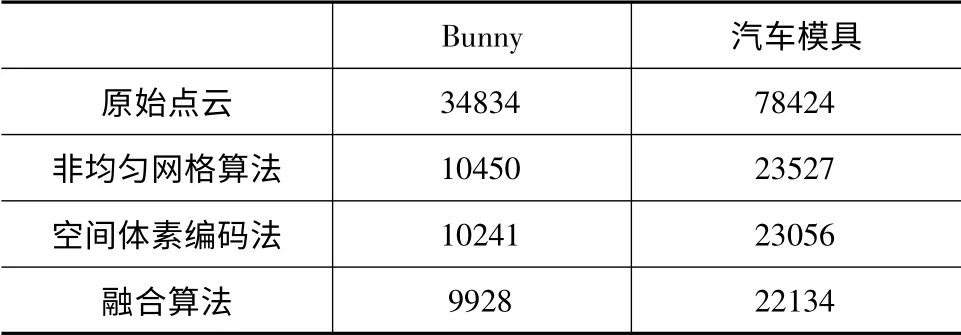
表2 實例點云數據

圖5為實驗簡化效果圖，通過上面實驗可以得出，本文算法能夠有效簡化物體的點云數據，又能保證物體形狀特征。空間體素編碼法簡化效率優于非均勻網格算法。本文提出的融合算法簡化效率優于非均勻網格算法和空間體素編碼法。Bunny模型和汽車模具在融合算法下，基本保留了模型數據的表面特征，簡化數據量最少，而非均勻網格算法，簡化數據明顯較多;采用體素編碼算法，簡化數據比非均勻網格算法少。由此可見，本文融合算法的簡化效率較好。本算法中的T值根據模型的曲率和形狀是可調的。

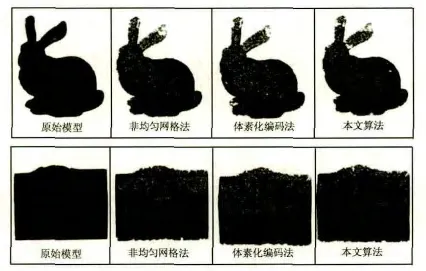
圖5 簡化效果圖

實驗還對本文所提出的算法與文獻［12］算法在點云簡化時間上做了比較，本文算法在對Bunny模型簡化耗時0．76 s，對汽車模具簡化耗時0．94 s;而文獻［12］算法對Bunny模型簡化耗時0．87 s，對汽車模具簡化耗時1．03 s。可見，本文算法的簡化運行速度優于文獻［12］算法速度，具有較好的實用性。

5．2 簡化誤差分析

為了評價簡化點云集的準確性，在原始點云集和簡化點云集之間的幾何誤差，Cignoni等［11］開發了Metro工具來比較曲面直徑的誤差。Pauly等［12］和Miao等［13］采用了相似的方法來評估簡化誤差。本文采用了原始點云集S和簡化后的點云集S'的最大誤差和平均誤差［14］。

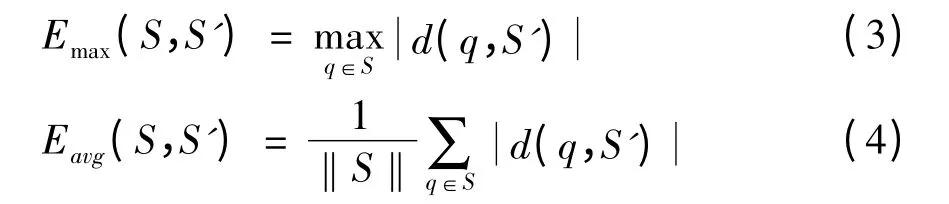
其中，每個點q∈S，幾何誤差d(q，S')是采樣點q和它在簡化點云曲面S'上的投影點q－之間的歐幾里德距離。點云簡化誤差如表3所示。

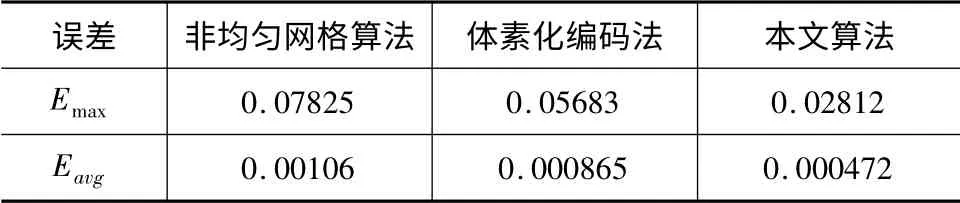
表3 點云簡化誤差

使用本文提出的融合算法的最大誤差和平均誤差比非均勻網格算法和體素化編碼法要小。可見其有效性較好。

6 結論

點云簡化可刪除大量冗余點云，而常用的非均勻網格法簡化點云存在簡化效率不高，容易丟失細節信息和關鍵特征的缺點。本文提出局部和全局特征法簡化無序點云，根據調整T值靈活控制局部特征和全局特征所占權重，達到刪減冗余點云數據的最好效果。實驗例證本文算法簡化點云數據既能保留突變區細節特征，又能大量刪除平坦區冗余點云數據，相比非均勻網格法和空間體素法，具有更高的點云簡化效率，而且簡化誤差也比較小。

［1］ LIU Weijun，SUN Yuwen．Principal，method and application of reverse Engineering［M］．Beijing:Mechanical industry press，2008．(in Chinese)劉偉軍，孫玉文．逆向工程原理方法及應用［M］．北京:機械工業出版社，2008．

［2］ ZHANG Guoxiong．Three coordinate measuring machine［M］．Tianjin:tianjin university press，1999．(in Chinese)張國雄．三坐標測量機［M］．天津:天津大學出版社，1999．

［3］ Lee K H，Woo H，Suk T．Point data reduction using 3D grids［J］．The International Journal of Advanced Manufacturing Technology，2001，17(3):735－743．

［4］ LIU Deping，CHEN Jianjun．Point data reduction technique in reverse engineering［J］．Journal of xidiann university，2008，35(2):334－339．(in Chinese)劉德平，陳建軍．逆向工程中數據精簡技術的研究［J］．西安電子科技大學學報，2008，35(2):334－339．

［5］ Martin R R，Stroud I A，Marshal A D．Data reduction for reverse engineering Reccad deliverable document Icoperunicus project［J］．Computer and Automation Institute of Hungarian Academy of Science，1996，1068:63－6．

［6］ SUN W，Bradley C，ZHANGY F，et al，Cloud data modeling employing a unified non－redundant triangular mesh［J］．Computer Aided Design，2001，33(2):183－193．

［7］ Chen Y H，Neg C T，Wang Y Z．Data reduction integrated reverse engineering and rapid prototyping［J］．International Journal of Computer Integrated Manufacturing，1999，12(2):97－103．

［8］ SUN Dianzhu，ZHU Changzhi，FAN Zhixian．Reduction algorithm for scattered points based on model surface analysis［J］．China mechanical engineering，2009，20(23):2840－2843．(in Chinese)孫殿柱，朱昌志，范志先，等．基于型面特征的三維散亂點云精簡算法［J］．中國機械工程，2009，20(23):2840－2843．

［9］ ZHOU Yu，ZHANG Wanbing，DU Farong．Algorithm for reduction of scattered point cloud data based on curvature［J］．Journal of Beijing Institute of Technology，2010，30(7):785－789．(in Chinese)周煜，張萬兵，杜發榮，等．散亂點云數據的曲率精簡算法［J］．北京理工大學學報，2010，30(7):785－789．

［10］Veron P，Leon J C．Static polyhedron simplification using error measurement［J］．Computer Aided Design，1997，29:287－298．

［11］Cinnoni P，Rocchini C，Scipigno R．Metro:measuring error on simplified surfaces［J］．Computer Graphics Forum 1998，17(2):167－174．

［12］Pauly M，Gross M，Kobbelt L P．Efficient simplification of point－sampled surfaces［C］．Proceeding of the 13thIEEE visualization conference，2012:163－170．

［13］Miao Y，Pajarola R，Feng J．Curvature－aware adaptive re－sampling for point－sampled geometry［J］．Computer－Aided Design，2009，41(6):395－403．

［14］Baoquan Shi，Jin Liang，Qing Liu．Adaptive simplification of point cloud using K－means clustering［J］．Computer－Aided Design，2011，43(1):910－922．