具有碰撞角約束的微分對策導引律研究*

徐興元,蔡遠利

(1 河南科技大學信息工程學院,河南洛陽 471023;2 中國空空導彈研究院,河南洛陽 471009;3 西安交通大學電子與信息工程學院,西安 710049)

具有碰撞角約束的微分對策導引律研究*

徐興元1,2,蔡遠利3

(1 河南科技大學信息工程學院,河南洛陽 471023;2 中國空空導彈研究院,河南洛陽 471009;3 西安交通大學電子與信息工程學院,西安 710049)

控制碰撞角度可以提高攔截彈的打擊效果。文中提出了一種具有碰撞角約束的微分對策導引律,能夠同時對脫靶量和碰撞角進行控制。把攔截彈和目標當作兩個獨立的受控對象,通過最小化代價函數同時得到了攔截彈的最優機動策略和目標的最優逃避策略。仿真結果表明,文中提出的微分對策導引律適用于攔截高速機動目標,而且在滿足厘米級脫靶量的情況下,攔截彈在交匯點處不需要過大的橫向加速度指令,從而避免指令被限幅。

攔截彈;碰撞角;微分對策導引律;機動目標

0 引言

傳統的比例導引律不能實現對終端碰撞角度的控制,但是一些比例導引律的變種形式,可以實現預先確定的碰撞角度[1-4]。偏差比例導引律[1]是在傳統的比例導引律的基礎上再加上一項隨時間變化的偏差項,這一偏差項可以使導彈以特定的角度碰撞目標。橢圓弧導引律[2]是另一種針對靜止目標的偏差比例導引律,這種制導方法假定導彈始終位于一條預先確定的連接導彈和目標的橢圓弧上,且所需的終端速度方向位于目標點的切線上,因此只要控制導彈沿該橢圓飛行,即可在命中目標的同時滿足碰撞角度要求。變系數比例導引律[3]是根據彈目運動的數學模型,通過在線調整導引系數以滿足終端角度約束的一類導引律。基于虛擬目標的軌跡預測比例導引律[4]首先設計以期望角度向真實目標運動的虛擬目標,然后控制導彈追蹤此虛擬目標并保證終端時刻形成尾追狀態,從而滿足末速方向要求。上述幾種比例導引律的變種形式都具有制導形式簡單,對導航信息偏差的敏感性較低的優點,但所得到的導引律依賴于各種假設與簡化,僅適用于靜止目標或者緩慢移動的目標。

以最優控制理論為基礎的最優導引律可以考慮導彈和目標的動力學問題,并可以考慮制導過程起點或終點的約束條件或其它約束條件,如能量消耗最少、終端脫靶量最小、最短時間、最小控制量、特定的碰撞角度等。Ryoo等[5]研究了勻速導彈具有碰撞角度和控制量約束的最優導引律。Sang等[6]提出了基于李雅普諾夫穩定理論和參數最優化方法的碰撞角控制導引律。Lee等[7]提出了同時控制時間和碰撞角度的最優導引律。Lee等[8]設計了同時滿足終端角度和加速度約束的最優導引律。最優導引律的缺點體現在,對目標加速度估計誤差、剩余飛行時間估計誤差靈敏度高,對測量元件也提出很高的要求。另外,最優導引魯棒性較差。

微分對策的概念早在20世紀50年代就提出來了,但一直未在導彈制導領域得到重視。微分對策導引律是將最優控制與對策論相結合得到的。微分對策導引律與最優導引律的區別在于:最優導引律是一個單邊優化問題,所得到的僅僅是攔截彈的最優機動策略;而微分對策導引律是一個雙邊優化問題,通過最小化代價函數同時得到攔截彈的最優機動策略和目標的最優逃避策略。由于在實戰中導彈和目標是一對獨立受控對象。顯然,基于“零和博弈”思想的微分對策導引律更符合工程需要。

總體來講,現有的各種具有角度約束的導引律,針對靜止目標或者緩慢移動的目標具有較好的性能,而對于高速機動目標,這些導引律往往并不具備足夠高的精度。原因在于過小的脫靶量往往需要攔截彈在交匯點處提供很大的橫向加速度,甚至造成制導指令被限幅,引起脫靶。文中提出的具有碰撞角約束的微分對策導引律可以克服這一問題。

1 問題描述與建模

末制導段的彈目運動關系如圖1所示。假定攔截彈和目標的運動為二維平面飛行,二者的速度均為常量。由于末段飛行時間較短,假定攔截彈和目標速度與初始視線的夾角為小量,運動方程可以沿初始視線線性化。

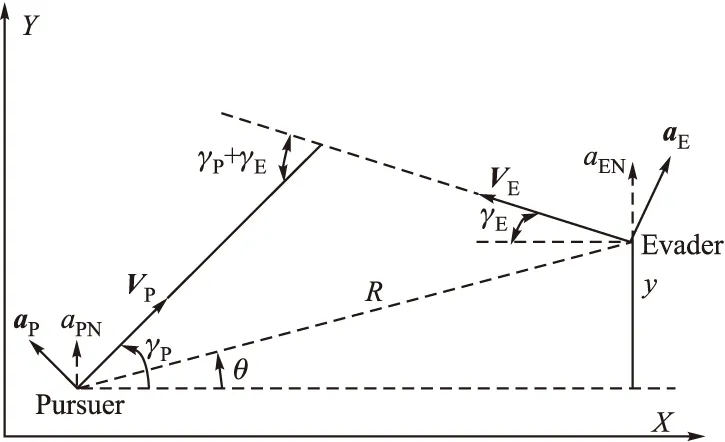
圖1 攔截彈和目標平面飛行簡圖

圖1中,X軸沿初始視線方向;下標P(Pursuer)表示攔截彈的相關狀態,下標E(Evader)表示目標的相關狀態;VP和VE分別為攔截彈和目標的速度;aP和aE分別為攔截彈和目標的橫向加速度;γP和γE分別為攔截彈和目標的彈道傾角;彈目相對距離為R;θ為視線角;彈目雙方偏離初始視線的相對位移表示為y。aP和aE垂直于X軸的分量表示為aPN和aEN,且aPN=aPcosγP0,aEN=aEcosγE0。根據各個物理量的定義,彈目相對運動方程[9]為:

(1)

(2)

(3)

(4)

假定目標的橫向加速度是一階滯后的,則:

(5)

為了較好的表達文中的研究思想,把攔截彈當作零階滯后系統處理,即:

(6)

如果考慮系統滯后,可以按照類似的方法處理,但導出的導引律形式要復雜得多。

根據上文的描述,給出如下線性系統模型:

(7)

式中:狀態變量x1=y;x2為彈目相對橫向加速度;x3為目標的橫向加速度;x4為期望碰撞角度,x4=γP+γE。

系統狀態方程為

(8)

式中:uP為攔截彈的制導指令;uE為目標彈的制導指令。根據式(7)～式(8)有:

(9)

(10)

假定在中制導律的作用下,γP+γE大致滿足期望的碰撞角,而且彈目雙方在飛行末段偏離飛行三角形小量。因此,三角形得以維持,彈目接近速度近似為常量,剩余飛行時間用下式估計[9]:

(11)

2 導引律推導

考慮到終端狀態誤差最小和最少的能量消耗,定義線性二次型性能指標為[10]:

(12)

式中:e(tf)=x(tf)-xf為終端狀態誤差,xf為期望狀態。(e(tf))TSe(tf)體現了對終端狀態誤差的約束。最小化代價函數(12)分別得到滿足終端狀態誤差的攔截彈最小控制量uP(t)和目標彈最大控制量uE(t)。μ為彈目雙方機動能力的比值。文中的導引律要求對脫靶量和碰撞角度進行控制,也就是控制狀態x1和x4,通過下式對系統簡化。

(13)

式中:Ω(tf,t)為狀態轉移矩陣;D為一常矩陣,且:

(14)

Ω(tf,t)=

(15)

新變量Z(t)的導數為:

(16)

選取加權矩陣:

(17)

式中a1和a2為非負常數。定義γf=γP+γE,tg=tf-t,代價函數式(12)變為:

(18)

當考慮目標橫向加速度滯后時,所得到的導引律形式比較復雜,下面僅給出目標橫向加速度零滯后,即τE=0時的導引律。令τE=0,則:

(19)

(20)

利用最優控制理論的方法,根據式(18)～式(20),求解出攔截彈和目標的最優制導律分別為:

(21)

式中:

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

引入變量Z(t),不僅使問題得到了簡化,而且Z(t)有重要的物理意義。Z1(t)表示零控脫靶量,Z2(t)表示零控碰撞角。Z1(t)和Z2(t)如下式所示:

(31)

(32)

為了應用式(21)所示的微分對策制導律,攔截彈需要獲取必要的信息。假定攔截彈能夠獲取視線角θ(t)的信息且θ(t)為小量,則y≈θR,有:

(33)

3 性能分析

利用表1所示的參數驗證所提出導引律的有效性。所得的仿真結果如圖2～圖6所示。圖2表示具有各種碰撞角的彈目飛行軌跡;圖3表示對應圖2中各條飛行軌跡的攔截彈最優制導指令;圖4表示對應圖2中各條飛行軌跡的目標彈最優制導指令;圖5表示脫靶量的變化;圖6表示碰撞角的變化。仿真結果表明,在滿足0.1 m脫靶量的條件下,能夠同時控制碰撞角度,且所需的制導指令不大,可以避免指令被限幅。另外,在仿真時假定攔截彈和目標的速度均為1 500 m/s,也就是說,攔截彈相對于目標并沒有速度優勢,這是所提出導引律的一大優勢。由圖3看出,當碰撞角太大時,攔截彈的最大制導指令明顯變大,因此,對于特定的碰撞角,選擇合適的初始角度可以有效減小最大制導指令。

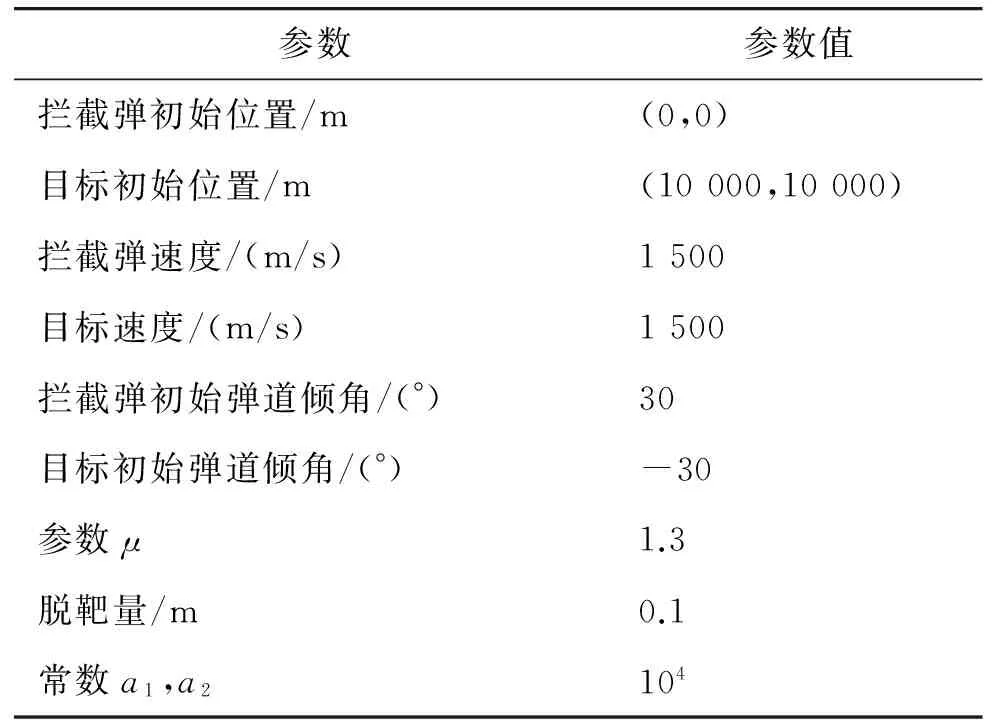
表1 非線性仿真的初始參數

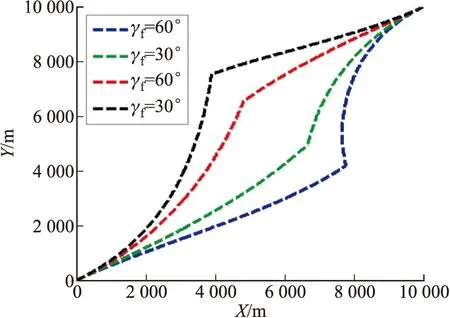
圖2 彈目飛行軌跡

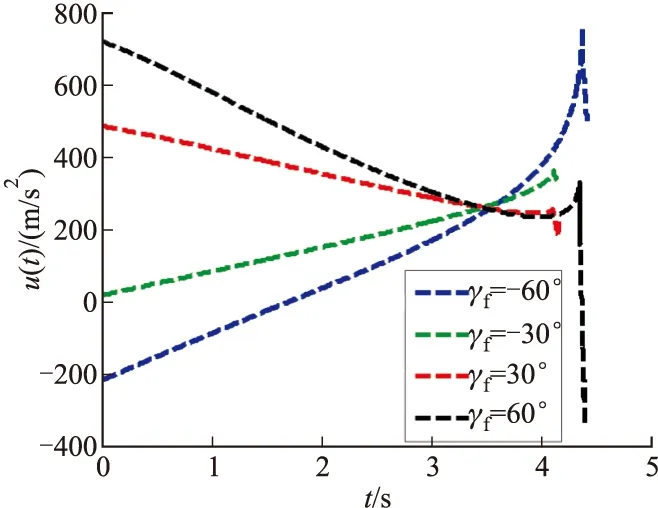
圖3 攔截彈制導指令

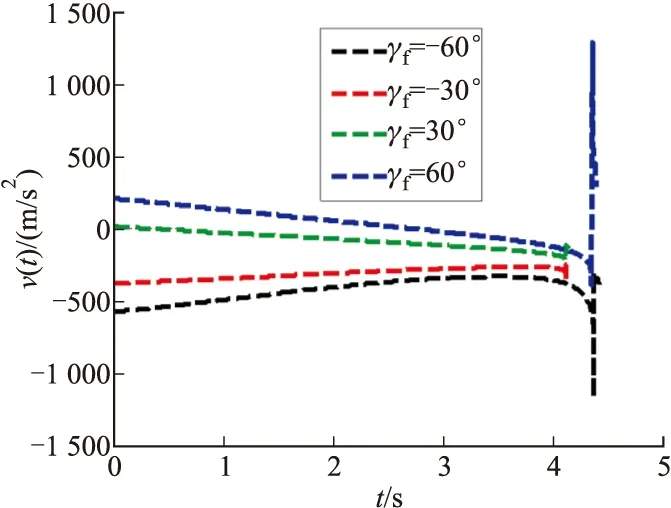
圖4 目標彈制導指令

圖5 脫靶量的變化

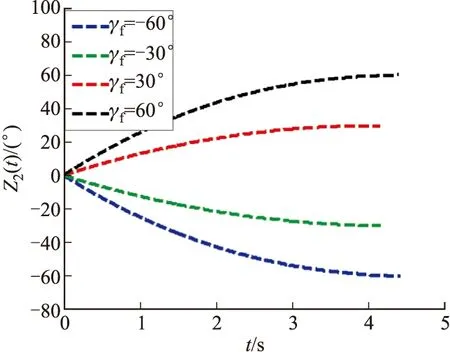
圖6 碰撞角的變化

4 結束語

文中提出了一種具有碰撞角約束的微分對策導引律,文中給出了較詳細的推導過程并通過數字仿真驗證了其有效性。當設定脫靶量為0.1 m,攔截彈和目標具有相同的初始速度時,攔截彈在交匯點處不需要太大的橫向加速度指令。雖然微分對策導引律是在假定彈目雙方偏離初始視線小量的情況下,通過運動方程線性化得到的,但仿真結果表明彈目雙方偏離初始視線較大時,導引律仍然具有很好的性能。

文中提出的微分對策導引律依賴精確估計剩余飛行時間,因此研究更精確的估計剩余飛行時間的方法是必要的。另外,攔截彈初始發射角度對制導性能有很重要的影響,對于特定的碰撞角,選擇合適的初始角度可以減小最大制導指令,這也是今后的一個研究內容。

[1] Kim K S, Jung B, Kim Y. Practical guidance law controlling impact angle [J]. Journal of Aerospace Engineering, 2007, 221(1): 29-36.

[2] Yoon M G. Relative circular navigation guidance for three-dimensional impact angle control problem [J]. Journal of Aerospace Engineering, 2010, 23(4): 300-308.

[3] 朱戰霞, 王建培. 一種攻擊地面固定目標的變系數比例導引律 [J]. 飛行力學, 2000, 18(4): 46-49.

[4] 張汝川, 顧文錦, 趙紅超. 基于落角約束的超聲速導彈制導方案研究 [J]. 飛行力學, 2009, 27(3): 45-49.

[5] Ryoo C K, Shin H S, Tahk MJ. Energy optimal waypoint guidance synthesis for antiship missiles [J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 80-95.

[6] Sang D, Min B M, Tahk M J. Impact angle control guidance law using Lyapunov function and PSO method [C]∥ SICE Annual Conference, Kagawa University, Japan, 2007.

[7] Lee J I, Jeon I S, Tahk M J. Guidance law to control impact time and angle [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 301-310.

[8] Lee Y, Ryoo C, Kim E. Optimal guidance with constraints on impact angle and terminal acceleration [C]∥AIAA Guidance, Navigation and Control Conference, Austin, USA, 2003.

[9] George M Siouris. Missile guidance and control systems [M]. New York, USA, Springer, 2004: 181-207.

[10] 吳受章. 最優控制理論與應用 [M]. 北京: 機械工業出版社, 2008: 59-75.

Differential Game Guidance Law with Impact Angle Constraint

XU Xingyuan1,2,CAI Yuanli3

(1 Information Engineering College，Henan University of Science and Technology, Henan Luoyang 471023, China;2 China Airborne Missile Academy, Henan Luoyang 471023, China;3 School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710079, China)

Control of impact angle can considerably increase interceptor’s lethality in terminal engagement. A differential game guidance law was proposed in this paper, which can achieve a specified impact angle as well as zero terminal miss distance. The adversaries in conflict were considered as two independent controlled objects, through minimizing the cost function, one can obtain the adversary’s optimal maneuver strategy simultaneously. Simulation results show that the proposed guidance law is suitable for intercepting high-speed maneuvering target., and, centimeter level miss distance requires less guidance command to avoid command saturation near terminal time.

antimissile interceptor; impact angle; differential game guidance law; target maneuver

2014-07-29

中國博士后科學基金(2013M542002);航空科學基金(20130142002)資助

徐興元(1972-),男,河南洛陽人,博士,研究方向:導航、制導與控制。

V249.12

A