基于FLcom 的模糊知識推理與搜索處理

趙潔心，潘正華，王姍姍

ZHAO Jiexin,PAN Zhenghua,WANG Shanshan

江南大學 理學院，江蘇 無錫214122

School of Science,Jiangnan University,Wuxi,Jiangsu 214122,China

1 引言

在知識表示與知識推理等研究中，對于知識中的否定的認知和處理一直以經典邏輯為基礎。隨著知識處理研究的發展，近年來一些學者主張知識處理領域中需要兩種否定。自1991 年，Wagner 等人區分強否定（strong negation）表示明確的假（explicit falsity）和弱否定（weak negation）表示非-真（non-truth）[1-5]。2005 年Kaneiwa 在描述邏輯中主張兩種否定，從而提出一個帶有經典否定和強否定的擴展的描述邏輯ALC～。2006 年Ferré提出一種認識的擴充，即基于模態邏輯AIK（All I Know）的一種邏輯轉化運用在邏輯概念分析LCA（Logical Concept Analysis）的框架中[6]。2006 年潘正華等人從概念層面上提出在知識處理中區分知識的矛盾關系和對立關系，研究指出了清晰性知識和模糊性知識中存在五種矛盾否定關系與對立否定關系，給出了它們的一種邏輯描述，并運用在知識表示與知識推理中[7-9]。為了能夠從邏輯的角度描述模糊知識中的不同否定及其關系與規律，2013 年潘正華又提出一種區分矛盾否定、對立否定和中介否定的模糊命題邏輯形式系統FLcom，并討論了其特有的性質與意義，給出了FLcom 的一種語義解釋[10]。

本文基于模糊命題邏輯形式系統FLcom 描述模糊知識，對帶有多種否定的模糊知識推理及搜索處理做了研究，將模糊知識以模糊命題的形式表現出來，并根據FLcom 對模糊命題形式表示和語義解釋將知識推理規則用模糊命題合式公式表示，合理定義了推理規則中結點否定形式的算子。給出實現搜索的算法和交通事故模型中模糊知識的推理過程與搜索結果。

2 基礎

2.1 單鏈表

單鏈表[11]是線性表的一種非順序存儲表示，屬于非數值計算領域的數學模型—線性結構的范疇。單鏈表用一組地址任意的存儲單元存放線性表中的數據元素。表中的一個單元可以看成一個結點，每個結點除了存放數據以外，必須設一個指針域，便于聯接下一個結點。數據域用來存儲結點的值；指針域用來存儲數據元素的直接后繼的地址（或位置）。

這里采用尾插法建立單鏈表[12]。頭指針head 指向頭結點，并設置兩個指針r、s。起始狀態是三個指針同時指向頭結點。申請新結點為s指向，修改指針r→next=s，最終r結點指向終端結點。如圖1 所示。

圖1 單鏈表的建立

由單鏈表的建立過程可以知道單鏈表中借用指針來表示數據元素間的邏輯關系，且每個結點僅包含一個指向后繼元素的指針。單鏈表只可向一個方向遍歷。表中的數據元素對應的結點包括兩個域：指針域和數據域。

2.2 區分矛盾否定、對立否定和中介否定的模糊命題邏輯形式系統FLcom

定義1[10]（I）設S是非空集，其元素稱為原子命題或原子公式，“?”，“ ╕”，“～”，“→”，“∧”和“∨”是連接詞，“（”與“）”是括號。規定：

（1）對每個A∈S，A是模糊命題。

（2）若A和B是模糊命題，則?A，╕A，～A，(A→B)，(A∨B)和(A∧B)是模糊命題。

（3）由（1）與（2）生成的全體模糊命題集為?(S)，簡記為?。? 中的元素稱為模糊公式，簡稱公式。

（II）? 中的以下公式稱為公理：

（A1）A→(B→A)

（A2） (A→(A→B))→(A→B)

（A3） (A→B)→((B→C)→(A→C))

（M1） (A→?B)→(B→?A)

（M2） (A→╕B)→(B→╕A)

（H） ?A→(A→B)

（C） ((A→?A)→B)→((A→B)→B)

（∨1）A→A∨B

（∨2）B→A∨B

（∧1）A∧B→A

（∧2）A∧B→B

（Y ╕） ╕A→?A∧?～A

（Y～） ～A→?A∧?╕A

（III）推理規則MP（Modus Ponens）：由A→B與A推出B。

由（I）、（II）和（III）構成的形式系統，稱為區分矛盾否定、對立否定和中介否定的模糊命題邏輯形式系統FLcom（Fuzzy propositional Logic with Contradictory negation，Opposite negation and Medium negation）。

FLcom是基于模糊集FScom基礎上提出的一種區分矛盾否定、對立否定和中介否定的模糊命題邏輯形式系統。在FScom 中，已證明一個模糊集P的矛盾否定P?與對立否定P╕和中介否定P～具有關系：P?=P╕∪P～，根據上述，即是?P=╕P∪～P。

在FLcom 中模糊公式?A，╕A和～A的關系定義如下[10]：

定義2在FLcom 中，?A=╕A∨～A。

2.3 FLcom 的一種語義解釋

定義3[10]設λ∈(0,1)。映射?：? →[0,1]稱為?的一個λ-賦值，如果：

（1）?(A)+?(╕A)=1

（2）?(～A)=

（3）?(A∨B)=max(?(A),?(B)),?(A∧B)=min(?(A),?(B))

（4）?(A→B)=?(?(A),?(B))

這里? ：[0,1]2→[0,1]是某個二元函數。

定義4[10]（λ-重言式）設?是Σ的λ-賦值集，?A∈Σ。如果對每個ξ∈?，恒有ξ(A)=1，則稱A為?-重言式。如果λ＞1/2 時，使得對每個λ-賦值ξ，恒有ξ(A)≥λ，則稱A為λ-重言式。

3 模糊知識的狀態空間表達式

3.1 基于模糊命題邏輯形式系統FLcom 的模糊命題表示

模糊命題主要由模糊概念構成，模糊命題的真值函數本身也必須與現實概念結合起來才有意義。要描述推理規則中的模糊命題，首先要對模糊命題中涉及的模糊概念進行描述。在對概念進行描述時，首先應確定對應類具有相同內涵的全體語言概念的集合，選取此內涵的更高級概念中區別最大的兩個模糊概念最為對立概念，并將其中之一用相應的[0，1]上的模糊子集表示[8]。由文獻[13]知，其余概念對應的表示可以得出。從而模糊命題及其不同否定也可以表示出來。

在數據庫中，知識以規則形式存在。設其中某個原子模糊命題為P，沿用FLcom 中的符號，其矛盾的模糊命題即表示為?P，對立的模糊命題為╕P，中介模糊命題為～P，或者可以根據需要將不同的模糊命題組合成合式公式來表達各種復雜的事實和命題。如此，對于命題?P，╕P，～P，可以根據不同的前綴做出相應的處理。這樣大大減少了數據庫中原子模糊命題的存儲量，減少了搜索時間。

為利于計算機實現，只研究規則庫中含有FLcom 中的邏輯連接詞的情況。因而，在知識表示中也僅含邏輯連接詞：“?”，“ ╕”，“～”，“→”，“∧”和“∨”。在不考慮閾值時，將每條規則表示為“A→B，CF”形式，其中A、B為原子模糊命題或合式公式，CF表示此規則的置信度。

3.2 命題邏輯公式的單鏈表的表示

在推理過程中，推理規則中往往不是一個條件推出一個結果，會出現多個條件推出一個結果或一個條件推出多個結果的情況，而且不是所有的條件之間都有聯系，一個條件也會在不同的推理規則中出現。因而，將單鏈表的定義修改為：

定義5在單鏈表中，一個存儲單元為一個結點，每個單元保存兩個數據項，第一個數據項是數據（即原子模糊命題的形式表示與其真值），第二個數據項是指針，即與下一個結點的邏輯關系。在內存中指針域就是后繼結點的集合。結點之間用箭頭連接，箭頭上的數字表示箭頭連接的兩個結點之間關系的置信度。箭頭可以表示結點之間“蘊含”，“交”關系，即“→”，“∧”。

定義6規則路徑表是存儲推理規則、結點置信度、規則可信度并用于搜索處理的一種若干單鏈表的組合表，即它是由規則中若干個既含有數據域又含有指針域的多個結點鏈接而成的一種存儲結構，且每個結點與其后繼結點按順序存儲在內存表中，所有的邏輯推理與搜索處理都以既定規則為準。

下面就用單鏈表和規則路徑表表示模糊推理規則：

（1）多個條件推出一個結果：A1,A2,…,An→B，則它 可 分 離 成n條 規 則：A1→B,CF1;A2→B,CF2;…;An→B,CFn，CFi(i=1,2,…,n) 為每條規則的置信度。分離后的規則用單鏈表表示，并將這些單鏈表組合成規則路徑表，其中A1,A2,…,An，B是結點，如圖2 所示。

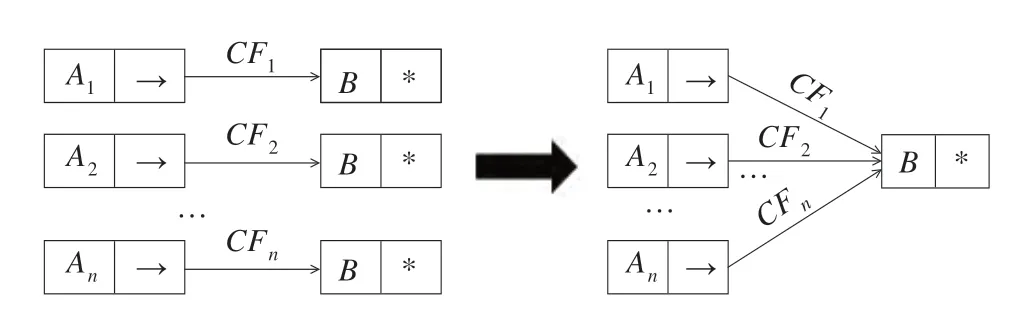
圖2 圖形演示一

（2）一個條件同時推出多個結果：A→B1,B2,…,Bn，則它可分離成n條規則：A→B1,CF1;A→B2,CF2;…;A→Bn,CFn。CFi(i=1,2,…,n) 為每條規則的置信度。分離后的規則用單鏈表表示，并將這些單鏈表組合成規則路徑表，其中A,B1,B2,…,Bn是結點，如圖3 所示。

圖3 圖形演示二

對于多維模糊規則：A1∧A2∧…∧An→B，直接用單鏈表表示，如圖4 所示。

圖4 圖形演示三

如圖2、圖3、圖4 所示，每個規則由結點，結點之間的邏輯關系和置信度組成，當規則運行時，從頭指針head 開始，頭指針指向單鏈表中的第一個結點。往往頭結點作為輸入結點，不同結點及其后繼結點依次從存儲表中提取出，依照推理規則在規則路徑表中展現它的邏輯狀態。這樣有利于快速搜索，減少數據訪問量，提高算法效率。

4 模糊知識推理的搜索方法

4.1 算法分析

在處理模糊知識時，問題的陳述和數據獲取方面固有的模糊性使得分析、解決問題時要處理大量模糊性的知識、概念，這樣得出的結果往往也具有模糊性。而且根據不同的實際情況可以推斷出多種結果，這就需要運用一定的策略得出最合理的結果。

本文用模糊推理的方法解決這一類模糊問題。模糊推理的基本原理就是根據已有的知識，建立推理規則推測未知知識[14]。在多層次模糊知識推理中，希望得到的是可能性最大的結果，因而問題轉化為根據已有的模糊推理規則尋找出最可能的結果，從而得出最佳路徑。在本文中尋找最佳路徑的過程就是尋找綜合可信度最大路徑問題。

為確定每一個表示模糊規則結論的結點所具有的真值或置信度，本文采用Zadeh 的CRI 算法[15]。Zadeh算子是模糊推理的CRI 框架中所用的t-范[15]，即a∨b=sup{a,b}，a∧b=inf{a,b}，同時也是格運算。基于Zadeh的CRI框架定義啟發函數：

f(n)=g(n)∧h(n)=min{g(n),h(n)}

其中，g(n)為頭結點到結點n的可信程度；h(n)為結點n到目標的估計可信度。在實際搜索中，可將初始條件真值程度視為頭結點的置信度，推理規則的置信度視為結點通過指針到達其后繼結點的可信度，推理結果為結點的置信度。

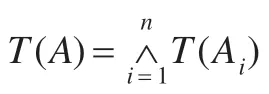
4.2 否定信息的處理

以上所述都是研究結點之間推理關系的推理規則及其表示，對于該文而言，結點就是原子模糊命題。上述搜索過程還需要具備解決結點中包含否定情形的能力，即解決模糊命題的矛盾否定(?)、對立否定(╕)和中介否定(～)的能力。

在規則庫中，多個規則之間通常存在一定聯系。但這種聯系有時又并非直接，例如：“A→B,CF1；╕B→C,CF2；～B→D,CF3；?B→E,CF4”。可以看出A與C、D、E之間通過B有間接聯系。為在搜索過程中體現這種聯系，將B、?B、╕B、～B都視為A的后繼結點，如此便能通過A間接推理到C、D或E。然而此時的問題是，規則庫中并沒有直接給出A→╕B，A→～B，或A→?B分別的置信度。在此，可先根據已知的規則求出B的置信度，然后采取一定的方法得出?B，╕B，～B。為使推理有序進行，在內存中存儲結點時將結點按照推理層次存儲，規則中的原子模糊命題及其不同否定在一個層次上，一個層次上的結點按指定順序存儲，如：B，?B，～B，╕B，如果其中的結點沒有參與推理，則不需要存儲在內存中。

針對具體實際領域，對知識庫中的每一個原子模糊命題A(x) 都賦予一個屬于[0，1]區間的真值，并確定l（規定λ＞0.5）作為滿足命題A的閾值。引用定義3 的符號，記?(A(x))為原子模糊命題A(x)的真值程度函數。

（1）根據定義3，?(A)+?(╕A)=1。因此，令對立否定“ ╕”的算子為：?(╕A(x))=1-?(A(x))。

（2）對于中介否定模糊命題～A(x)，由定義3 中式（1）～（5）可知，當λ＞1/2 時～A(x)的真值程度屬于區間(1-λ,λ)。但這種語義解釋沒有考慮A(x)的真值程度屬于區間[1-λ,λ]的情況，這樣就不能全面處理好否定信息，基于此，給出中介否定“～”的算子：

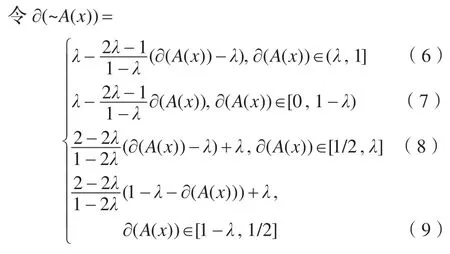
此算子在FLcom 的一種語義解釋的基礎上進行了修改，更符合人的思維習慣。在中介否定算子中，當λ＞1/2 時，式（6）中，當?(A(x))的取值從λ（不取λ）過渡到1 時，?(～A(x)) 從λ（不取λ）依次遞減到1-λ（不取1-λ）。式（7）中，當?(A(x))的取值從0 過渡到1-λ（不取1-λ）時?(～A(x))從λ（不取λ）依次遞減到1-λ（不取1-λ）。式（8）中，當?(A(x))從1/2過渡到λ時?(～A(x))從1遞減過渡到λ。式（9）中，當?(A(x))從1-λ過渡到1/2時?(～A(x))從λ遞增過渡到1。特別的，由式（8）、（9）還可以看出，當?(A(x))越接近1/2時，?(～A(x))的值越高。當?(A(x))=1/2 時?(～A(x))=1，這說明模糊命題A(x) 的模糊度比較高。

（3）根據定義2，有?A=╕A∨～A。因此，令矛盾否定“?”的算子為：?(?A)=max{?(╕A),?(～A)}。

5 具體實現

5.1 實例分析

下面討論模糊知識的推理與搜索處理的具體實例。推理規則：

（1）中年人是老練而穩重的，可信度較高；

（2）老練、穩重且有駕駛技術的人是不容易出交通事故的，可信度很高；

（3）駕駛技術熟練，熟悉交通規則又清醒駕駛的青年人不容易出交通事故，可信度較高；

（4）年紀大的人若疲勞駕駛較容易出交通事故，可信度較高；

（5）技術熟練的人比較熟悉交通規則，可信度高；

（6）駕駛技術不熟練的人容易出交通事故，可信度很高。

搜索條件：李先生50 歲并駕駛技術熟練；李先生可能有點疲勞。

根據FLcom 將這幾條規則轉化成模糊命題邏輯形式。令論域為所有人，X屬于論域。對于規則置信度，可根據實際情況對表示可信程度的語言賦值。在這個例子中，對“可信度很高”、“可信度較高”和“可信度高”分別賦予規則置信度值0.9、0.75、0.7；對“容易”、“較容易”和“不容易”分別賦予規則置信度值0.6、0.7、0.8。對“可能”賦予規則置信度值0.65。

根據文獻[13]，規則中的模糊概念“老年人”是“青年人”的對立否定；“中年人”是“青年人”的中介否定。顯然這三個概念內涵相同，但外延不同。將“X是青年人”作為原子模糊命題，表示為YOUNG（X），則～YOUNG（X）表示“X是中年人”；╕YOUNG（X）表示“X是老年人”。將“X是容易出交通事故的”作為原子模糊命題，表示為ACCIDENT（X）；～ACCIDENT（X）表示“X是較容易出交通事故的”；╕ACCIDENT（X）表示“X是不容易出交通事故的”。其余原子模糊命題表示為：AGE（X，Y），表示X的歲數為Y；TACT（X），表示X老練；STEADY（X），表示X穩重；SKILL（X），表示X駕駛技術熟練；?SKILL（X），表示X駕駛技術不熟練；FAMILIAR（X），表示X熟悉交通規則；～FAMILIAR（X），表示X較熟悉交通規則；TIRED（X），表示X疲勞駕駛；╕TIRED（X），表示X清醒駕駛。

那么，基于FLcom 和原子模糊命題的形式表示可以將規則表示成：

（1）～YOUNG（X）→TACT（X），CF=0.75；～YOUNG（X）→STEADY（X），CF=0.75。

（2）TACT（X）∧STEADY（X）∧SKILL（X）→╕ACCIDENT（X），CF=0.9。

（3）SKILL（X）∧FAMILIAR（X）∧╕TIRED（X）∧YOUNG（X）→╕ACCIDENT（X），CF=0.75。

（4）╕YOUNG（X）∧TIRED（X）→～ACCIDENT（X），CF=0.75。

（5）SKILL（X）→～FAMILIAR（X），CF=0.7。

（6）?SKILL（X）→ACCIDENT（X），CF=0.9。

搜索條件表示為：AGE（Li，50），SKILL（Li），CF=1；TIRED（Li），CF=0.65。

至此，發現需要確定此例中“李先生是中年人”的置信度。為此，首先選定“X是青年人”作為原子模糊命題。假如“X是青年人”一般認為X的年齡大概是20至30 歲，“X是老年人”一般認為X的年齡大概是60 至80 歲，“X是中年人”是他們之間的中介。此處只涉及到“年齡”這一因素，采用一維歐式距離d(x,y)=|x-y|以及“距離比率函數”[8]求出命題“李先生是青年人”的真值程度，即

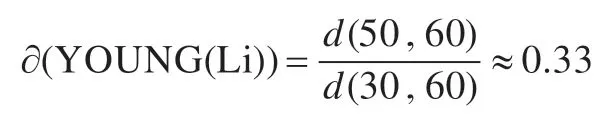
其中，d(x,y)表示x，y之間的一維歐氏距離，d(50,60)表示李先生的年齡與觀念上某人是老年人之間的距離，d(30,60)表示觀念上某人是青年人和某人是老年人之間的距離。兩者的比值表示模糊命題YOUNG（Li）的真值程度，由此可知，AGE（Li，50）→YOUNG（Li）的置信度為0.33。

假設閾值為λ=0.8，顯然1-λ＜?(YOUNG(Li))＜λ。根據4.2 節中式（9），?(～YOUNG(Li))≈0.887，由“ ╕”的算子，?(╕YOUNG(Li))=1-0.33=0.67。

下面是用規則路徑表表現出的搜索處理方法。

如表1，是交通事故模型中結點的存儲表；圖5 為交通事故模型的搜索過程。

表1 交通事故模型中結點的存儲表（頭指針）

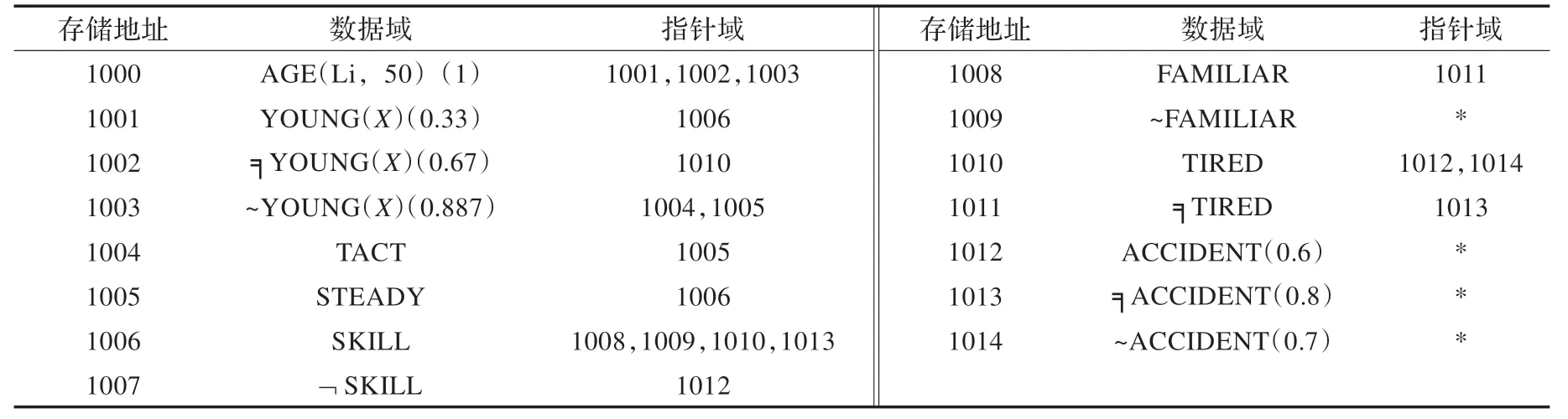
表1 交通事故模型中結點的存儲表（頭指針）

存儲地址1000 1001 1002 1003 1004 1005 1006 1007數據域AGE（Li，50）（1）YOUNG（X）（0.33）╕YOUNG（X）（0.67）～YOUNG（X）（0.887）TACT STEADY SKILL?SKILL指針域1001，1002，1003 1006 1010 1004，1005 1005 1006 1008，1009，1010，1013 1012存儲地址1008 1009 1010 1011 1012 1013 1014數據域FAMILIAR～FAMILIAR TIRED╕TIRED ACCIDENT（0.6）╕ACCIDENT（0.8）～ACCIDENT（0.7）指針域1011*1012，1014 1013***

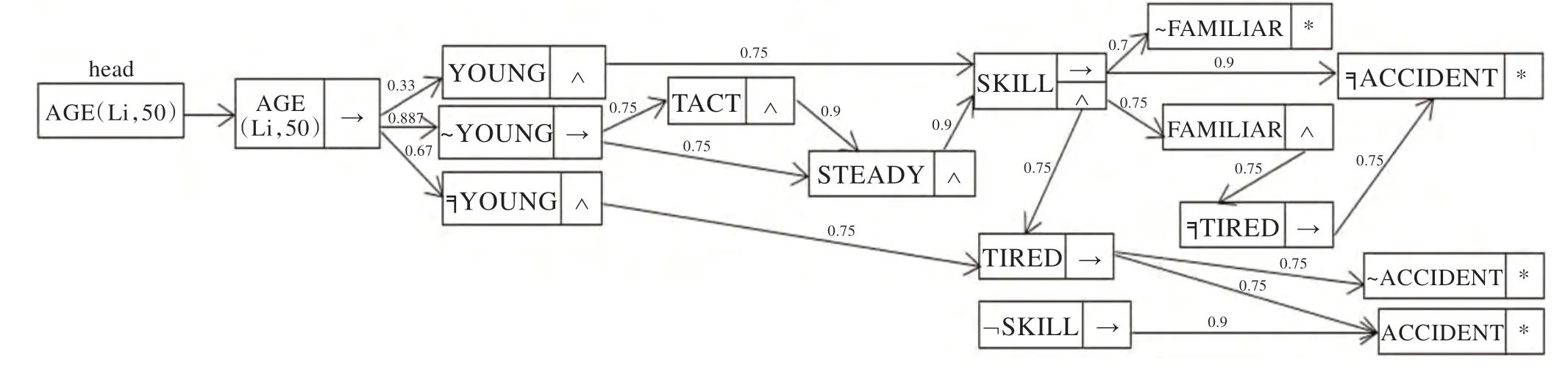
圖5 交通事故模型的搜索過程

5.2 算法實現

算法的具體實現過程：

（1）輸入初始結點START 作為頭結點，根據結點置信度的算子計算此結點的置信度值?(START)（結點的置信度也有可能依據實際情況事先給定），從內存中依次調用初始結點的指針域。

（2）如果指針域為空，則終止搜索。如果指針域不為空，運用CRI 算法計算指針域中結點的置信度，再提取出置信度值最大的結點（命名為NODE），并記錄上一個結點的指針和此結點。再從內存中調用此結點的指針域。

（3）如果指針域為空，則終止搜索，將?(NODE)賦值給?(START)。如果指針域不為空，重復步驟（2）。

（4）若?(START)＜μ則搜索失敗；若?(START)≥μ，則搜索成功。

（5）輸出搜索結果?(START)以及得出這個搜索結果的路徑，此搜索路徑為最佳搜索路徑，結束搜索。

由于推理規則中的原子模糊命題的數量是有限的，所以搜索結點也是有限的，那么算法只需從內存中做有限次的調用，從而算法必在有限步內終止。此算法在搜索過程中，需要規定一個搜索閾值，記為μ。若解結點的置信度值小于μ，則要放棄該搜索，即此解不可信。

根據上述算法的實現過程，由頭結點開始通過推理規則搜索可以找到被記錄的且滿足搜索閾值要求的置信度最高的終端結點。在5.1 節的實例中，將搜索閾值定為0.6。通過算法運行得出?(AGE(Li,50))=?(╕ACCIDENT(X))=0.9，即 到 結 點╕ACCIDENT(X)的搜索路徑最可信，從而可以推理出李先生不會出交通事故。

6 結束語

基于FLcom，研究模糊知識及其否定的形式表達。合理修改單鏈表，給出規則路徑表的定義，利用規則路徑表表示推理規則和搜索過程。結合模糊命題形式系統的語義解釋，給出中介否定(～)、對立否定(╕)和矛盾否定(?)的算子。將模糊知識推理和搜索處理方法、過程應用于交通事故模型，并通過模糊知識搜索處理算法來實現這一搜索過程。這樣的處理方法簡化了模糊知識推理過程，為模糊推理與搜索處理的計算機實現提供一種新思路。

[1] Wagner G.A database needs two kinds of negation[C]//Proceedings of the 3rd Symposium on MFDSB，May 6-9，1991，495：357-371.

[2] Wagner G.Web rules need two kinds of negation[C]//Proceedings of PPSWR’03，2003：33-50.

[3] Minker J，Ruiz C.Semantics for disjunctive logic programs with explicit and default negation[J].Fundamenta Informaticae，1994，20（3/4）：145-192.

[4] Dung P M，Mancarella P.Production systems need negation as failure[J].IEEE Transactions on Knowledge and Data Engineering，2002，14（2）：336-353.

[5] Vakarelov D.Nelson’s negation on the base of weaker versions of intuitionistic negation[J].Studia Logica，2005，80：393-430.

[6] Ferré S.Negation，opposition，and possibility in logical concept analysis[C]//Proceedings of the 4th International Conference on Formal Concept Analysis，Feb 13-17，2006，3874：130-145.

[7] Pan Zhenghua，Zhu Wujia.A new cognition and processing on contradictory knowledge[C]//Proceedings of the IEEEInternational Conference on Machine Learning and Cybernetics，Qingdao，China，2006：1532-1537.

[8] 王岑，潘正華，程天笑.基于中介邏輯的模糊知識推理的搜處理[J].計算機工程與應用，2009，45（21）：175-178.

[9] 潘正華.知識中不同否定關系的一種邏輯描述[J].自然科學進展，2008，18（11）：66-74.

[10] Pan Zhenghua.Three kinds of negation of fuzzy knowledge and their base of logic[C]//Proceedings of ICIC 2013，July 28-31，2013，7996：83-93.

[11] 謝娟英.單鏈表不同建立算法研究[J].現代電子技術，2010（4）：132-134.

[12] 史麗燕.單鏈表基本操作的實現[J].軟件導刊，2010（2）：21-22.

[13] 潘正華.模糊知識的三種否定及其集合基礎[J].計算機學報，2012，35（7）：1421-1428.

[14] 范世青，張文修.模糊概念格與模糊推理[J].模糊系統與數學，2006（1）：11-17.

[15] 吳望名.模糊推理的原理和方法[M].貴陽：貴州科技出版社，1994.