輪廓波系數引導的數字圖像修復算法研究
李宣妮,王慧琴,吳 萌
LI Xuanni,WANG Huiqin,WU Meng
西安建筑科技大學 信息與控制工程學院,西安710055
School of Information and Control Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China
1 引言
數字圖像修復是指對圖像局部區域內丟失或損壞的數據按照特定規則進行填補,以恢復整幅圖像的完整性和原有的視覺效果。它本身是一個病態問題,故不能保證完全正確地恢復圖像的被損壞部分,也就是說無法通過已知信息使圖像恢復原狀,因此需要加入合理的約束條件,使修復結果盡量滿足人的視覺心理需求。Criminisi等人[1]提出了基于樣本的圖像修復方法,在圖像信息完好區域中尋找與受損區域最匹配的像素塊,將其作為樣本填充到受損區域實現圖像修復。但由于算法本身的局限性,修復結果常出現紋理混亂和馬賽克效應,這一缺點在復雜紋理圖像的修復中更加明顯,另外該算法時間復雜度比較高,無法滿足大數據量圖像的修復需求。
為解決大數據量圖像修復需求的問題,本文研究了在輪廓波分解下的數字圖像修復技術。輪廓波(contourlet)變換是多尺度幾何分析工具,采用不可分離濾波器組建立多分辨率多方向率分析,能夠實現靈活的多分辨率、局部的、多方向性的圖像表示[2]。該變換不僅可以提供小波分解的主要特征,而且還能提供不同角度各向異性的方向信息,角度方向的個數可以調整,因此它可以很好地捕捉各種角度的圖像邊緣特征[3]。
2 提取圖像的輪廓波系數
輪廓波是由Do 和Vetterli 于2001 年構建的多尺度幾何分析工具,與小波相比,在處理二維甚至更高維含“非線性奇異”的信號時,高維小波基由于受到小波張量積方向局限性的影響,達不到理想的最優逼近。輪廓波是比小波更為“稀疏”的多尺度幾何分析表述工具,它不僅能夠提供任意方向上的信息,而且它使用了迭代濾波器,使得計算效率高且復雜度低。
輪廓波變換是利用類似于輪廓段(contour segment)的基結構來逼近圖像。如圖1,輪廓波基的支撐區間是具有隨尺度變化長寬的條形結構,具有方向性和各異性,用輪廓波系數表示圖像的紋理能量更加集中,這些系數在不同的分解尺度間有一定的相關性和延續性[4]。在某些分解子帶中,系數賦值變化較大,而某些子帶中系數賦值多為0。這種變化用系數的方差來衡量是最合適的,方差的大小表示所在分解子帶的能量變化強度。
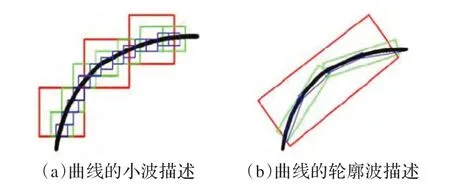
圖1 小波與輪廓波對曲線的描述
紋理圖像有豐富的邊緣信息和明顯的方向性,做輪廓波分解時能夠在某些方向的子帶中產生大量的分解系數,使在該方向的分解系數方差明顯增大。因此可以用輪廓波分解系數的方差來衡量圖像紋理能量變化的強弱[5],公式為:

其中,e為分解子帶的方差,i為分解尺度。
所以,子帶方差的大小可以作為該子帶能量變化強弱的指標。
3 基于樣本的圖像修復算法
基于樣本的圖像修復算法的實質是用等光照線驅動的圖像采樣的過程[6],將圖像源區域信息作為修復樣本填充圖像的待修復區域。其修復過程如圖2 所示。
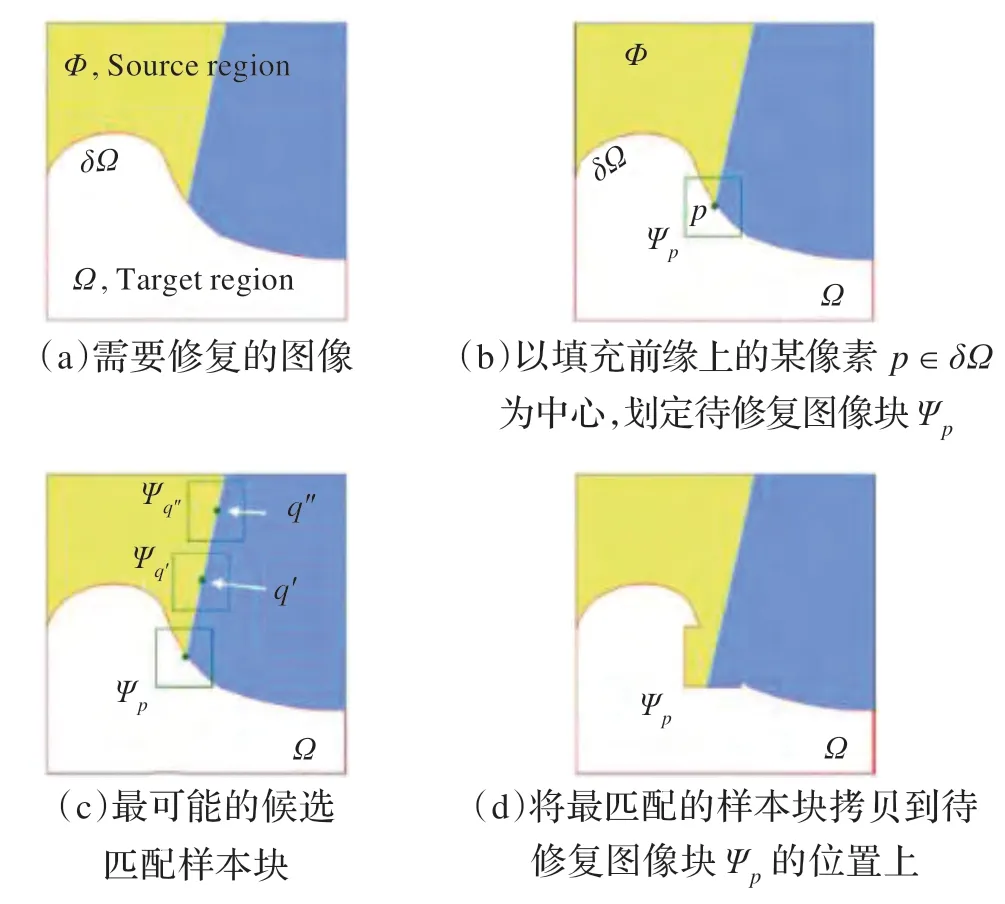
圖2 基于樣本的圖像修復算法的修復過程
圖3(a)為需要修復的圖像,Ω是圖像的待修復區域,?Ω是破損區域的填充前緣,Φ是源區域。圖(b)是以填充前緣上的某像素p∈δΩ為中心,劃定待修復圖像塊Ψp。圖(c)對待修復圖像塊Ψp來說,最可能的候選匹配樣本塊位于源區域中兩紋理之間的邊界上,如Ψq′,Ψq″。圖(d)是將最匹配的樣本塊拷貝到待修復圖像塊Ψp的位置上,實現了Ω的部分填充。這時,待修復區域Ω面積縮小,并產生新的填充前緣,最重要的是自動地保留了圖像等光照線的方向。圖像填充邊緣上的每個像素以此方法迭代執行,待修復區域Ω的面積不斷減小,直至為零。
優先值計算公式為:

其中,C(p)為置信度項,D(p)為數據項,且:
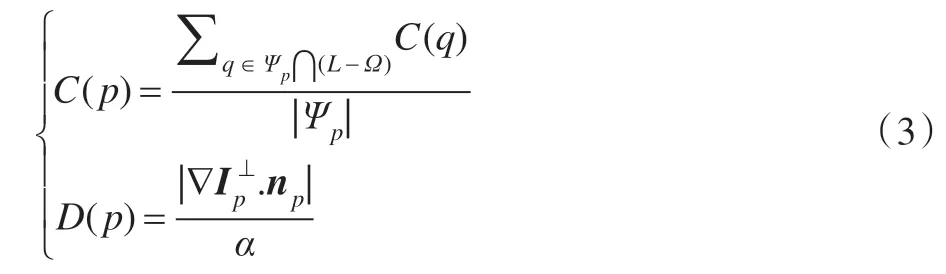
其中,|Ψp|是Ψp的面積,α為歸一化因子(對于常用的灰度圖像,α=255),是單位矢量:代表p點的等光照線方向,可以用灰度梯度表示,即(-Iy,Ix);np是填充前緣?Ω上p點處的法向量,可以用模板圖像I(0 表示待修復的像素點,1 表示沒有損壞的像素點的二值圖像)表示。Ix和Iy表示x方向和y方向的梯度,可得np=(Ix,Iy)。
圖3中修復結果出現了大塊的錯誤填充,由文獻[7-9]可知,圖像修復的結果與在修復過程中填充邊緣像素的修復順序有關。這是由于圖像修復的過程有時會沿著某一方向連續進行,使結果違反“人類視覺連通性”的原則,如圖4。
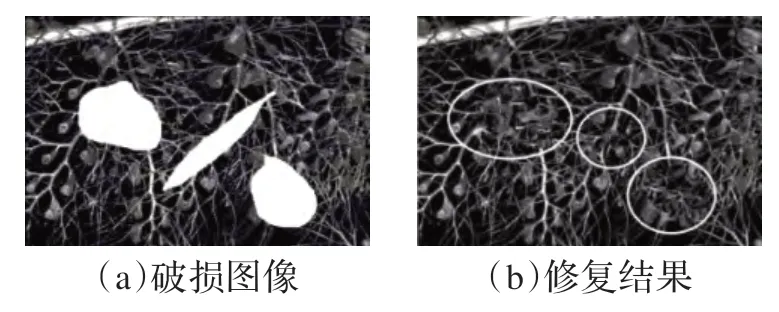
圖3 基于樣本的修復實驗
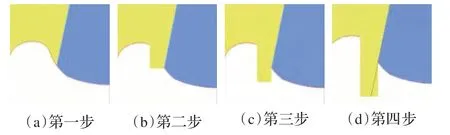
圖4 錯誤的圖像修復步驟
為避免圖4 情況的發生,在基于樣本的修復模型中引入輪廓波系數表示的圖像紋理能量信息,使填充邊緣上紋理的像素點能先修復。
4 輪廓波系數指導圖像修復
4.1 基本算法改進
圖像的邊緣和梯度值都反映圖像的紋理特征,當圖像在某一像素梯度值較大時說明在該像素點附近的圖像紋理較豐富[10-11]。
在公式(2)中引入β因子:

其中β大于1,表示圖像紋理能量的信息。改進的優先值公式考慮到輪廓波系數表示的圖像紋理能量,紋理能量越大的圖像塊優先值越大,越早被修復。
4.2 圖像紋理的輪廓波系數量化
由公式(1)可知,圖像的紋理越豐富,對應輪廓波系數的子帶方差越大,子帶能量越強。對于一幅大小為m×n的圖像,輪廓波系數的各子帶紋理能量可表示為:
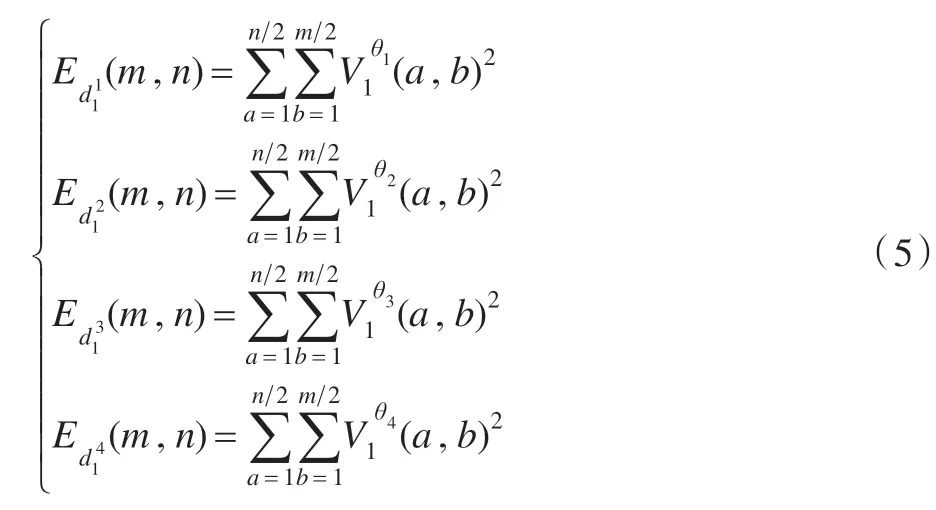
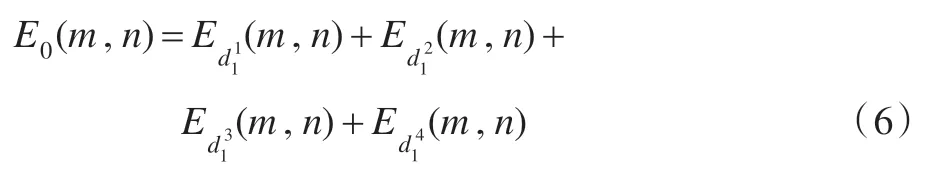
平均紋理能量為:

根據式(5)~(7)對圖像紋理程度的定義,計算圖5中圖像組的平均紋理能量,結果如表1 所示。

圖5 不同紋理特征的圖像

表1 圖5 中各圖像的紋理程度量化結果
可見,對于不同紋理程度的圖像,計算得到的紋理能量不同:越平滑的圖像,紋理能量越小;紋理越復雜的圖像,紋理能量越大。因此,可以根據圖像紋理能量的大小來引導圖像修復的過程,本文通過引入β因子實現這一過程。
4.3 β因子的自適應選擇

圖6 β值對修復結果的影響
對不同紋理程度的圖像進行修復仿真實驗,結果如表2 所示。可見,隨著圖像紋理越復雜,對應最佳β值的選取越大。
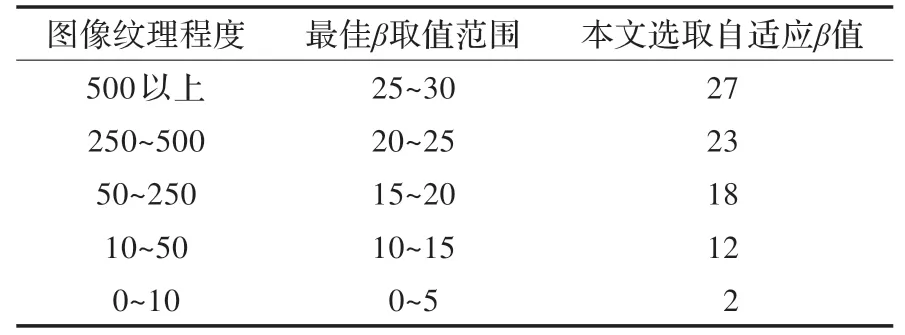
表2 自適應β值
4.4 本文算法實驗及對比分析
將本文算法分別與Criminisi 算法和利用小波系數修復的β方法進行比較,實驗結果及分析如下:
圖7 與圖8 是兩組修復實驗,兩組中的(a)為原圖,(b)為用Criminisi算法修復的結果,(c)為用基于小波系數的修復算法的修復結果,(d)為用本文算法修復的結果。

圖7 目標物去除效果比較

圖8 恢復破損圖像效果比較
就人眼直接觀察發現,圖7 與圖8 中的(b)圖和(c)圖均存在著不同程度的錯誤紋理堆積,(d)圖紋理比較自然。
計算圖7 與圖8 的三種算法修復結果的MSE(均方誤差)和修復耗時,結果如表3。
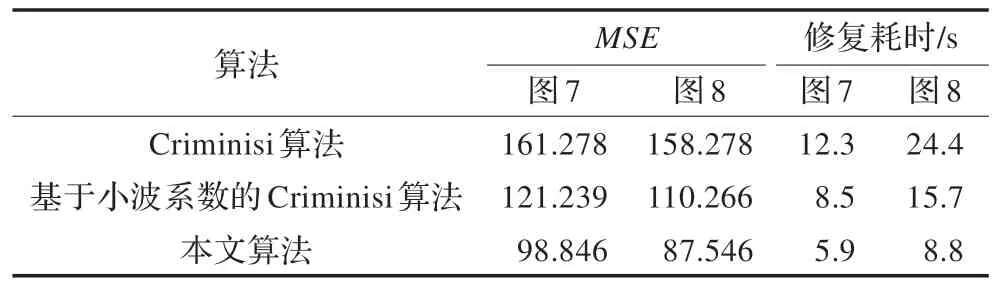
表3 圖7 與圖8 中三種修復算法客觀評價
分析表3 中數據:圖7 中使用本文算法與Criminisi算法相比,前者的MSE值降低了38.7%,修復耗時減少了52.0%;與用基于小波系數的Criminisi算法相比,本文算法的MSE值降低了18.5%,修復耗時減少了30.6%。圖8 中使用本文算法與Criminisi 算法相比,前者的MSE值降低了44.7%,修復耗時減少了63.9%;與用基于小波系數的Criminisi 算法相比,本文算法的MSE值降低了20.6%,修復耗時減少了43.9%。可見,無論是從主觀評價還是客觀評價來看,本文算法都優于Criminisi 算法和基于小波系數的Criminisi修復算法。
5 結束語
本文研究了輪廓波系數引導的基于樣本的圖像修復算法。實現了不同紋理特征圖像的自適應修復策略,先對圖像做輪廓波變換,提取輪廓波系數估計圖像紋理能量,根據紋理能量自適應選取β值,改進優先值計算公式,優化了圖像修復的順序,使修復對圖像的紋理特征更為敏感。通過實驗看出,本文算法在修復的效果和速率復雜度上都明顯優于Criminisi 算法和用小波系數修復圖像的算法。
[1] Criminisi A,Perez P,Toyama K.Region filling and object removal by exemplar-based image inpainting[J].IEEE Transactions on Image Processing,2004,13(9):1200-1212.
[2] Do M N,Vetterli M.The contourlet transform:an efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing,2005,14(12):2091-2106.
[3] Do M N,Vetterli M.Wavelet based texture retrieval using generalized Gaussian density[J].IEEE Transactions on Image Processing,2002,11(2):146-158.
[4] 郭蔚,李婷.輪廓波變換原理及其構造方法[J].數學進展,2012,41(3):266-275.
[5] 趙一凡,夏良正.基于輪廓波特征的紋理圖像識別方法[J].東南大學學報:自然科學版,2008(S2):128-131.
[6] 張偉彬.基于修復順序的圖像修復算法[J].計算機工程與應用,2008,44(22):195-196.
[7] 張紅英.數字圖像修復技術的研究與應用[D].成都:電子科技大學,2006.
[8] 王黎明.基于樣本塊的圖像修補方法研究[D].北京:首都師范大學,2008.
[9] Sun J,Yuan L.Image completion with structure propagation[J].ACM Transactions on Graphics,2005,3:861-868.
[10] 李一哲.基于樣圖的紋理合成技術研究[D].合肥:中國科技大學,2006.
[11] 陳卿,王慧琴,吳萌.基于紋理特征的自適應圖像修復算法[J].計算機應用,2011,6(6):1572-1574.

