火箭彈脈沖修正擾動運動仿真*

游培寒,繆 昕,喬治軍,祝逢春

(1 95856部隊,南京 210000;2解放軍理工大學理學院,南京 210007)

火箭彈脈沖修正擾動運動仿真*

游培寒1,繆 昕2,喬治軍1,祝逢春1

(1 95856部隊,南京 210000;2解放軍理工大學理學院,南京 210007)

為了構建火箭彈擾動運動半實物仿真,需要對火箭彈運動進行建模和簡化。文中分析影響火箭彈彈體擾動運動的主要因素,構建脈沖發(fā)動機工作時彈體擾動方程。利用火箭彈彈體與彈道夾角較小,以及脈沖發(fā)動機沖量方向和彈道垂直等特征,對擾動運動方程進行簡化,推導出縱向和側向彈體擾動運動模型,得到擾動運動衰減系數(shù)和彈體振蕩頻率的相關計算公式。仿真結果表明,新擾動運動模型能夠模擬火箭彈擾動運動。

脈沖發(fā)動機修正;擾動運動;彈道仿真

0 概述

彈體擾動運動仿真對火箭彈側姿系統(tǒng)驗證、修正方法研究等都有重要意義。文中以脈沖發(fā)動機修正為例,設計了一種能夠在實驗室環(huán)境下進行脈沖修正擾動運動仿真的建模方法。由于脈沖發(fā)動機工作時間短、沖量相對恒定,可以利用脈沖函數(shù)模擬其工作過程,利用拉氏變換對縱向和側向的擾動運動進行了推導,得出兩個方向的解析解,及擾動衰減系數(shù)和振蕩頻率等參數(shù)的計算方法,利用Simulink軟件進行擾動運動建模,建模運算結果與6自由度火箭彈彈體運動方程計算結果基本一致。文中第二部分介紹縱向和側向擾動運動方程;第三部分推導擾動運動的解析解并分析擾動運動各部分組成;第四部分介紹利用Simulink設計的火箭彈擾動運動模型,第五部分給出部分仿真結果。

1 縱向和側向脈沖擾動方程

假設火箭彈縱向脈沖修正時,彈體沒有側滑,則根據(jù)文獻[4],彈體縱向運動方程可以簡化為:

(1)

其中:X為阻力;Y為升力;G為重力;Fmc為脈沖修正力;Lmc為脈沖修正力臂長度;v為火箭彈速度標量;m為質(zhì)量;θ為速度俯仰角;?為彈體俯仰角;α為攻角;wz為俯仰角速度;Jz為俯仰轉動慣量;Mz是俯仰力矩。根據(jù)火箭彈的氣動特性,有如下關系:

(2)

(3)

將式(2)、式(3)代入式(1),可得到俯仰擾動運動方程為:

(4)

同理,可以推導出側向擾動運動方程,其中Jz為側向轉動慣量,由于彈體軸向對稱,有Jz=Jy,ψ是彈體航向角,ψv是速度航向角,wy是航向角速度,β是

側滑角。

(5)

2 縱向和側向運動解析

2.1 縱向脈沖擾動解析

對式(4)進行拉氏變換得到:

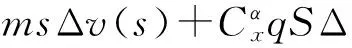
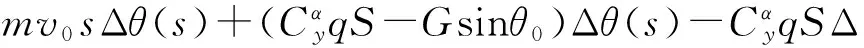
Fmc(s)

Jys2Δ?(s)-mwqSLsΔ?(s)-mαqSLΔ?(s)+

mαqSLΔθ(s)=LmcFmc(s)

(6)

2.1.1 速度俯仰角的解析解

從式(6)可得:

則可以推導出:

Δθ(s)=

θ0取值較小的情況下可以忽略mαqSLGsinθ0和mwqSLGsinθ0則有:

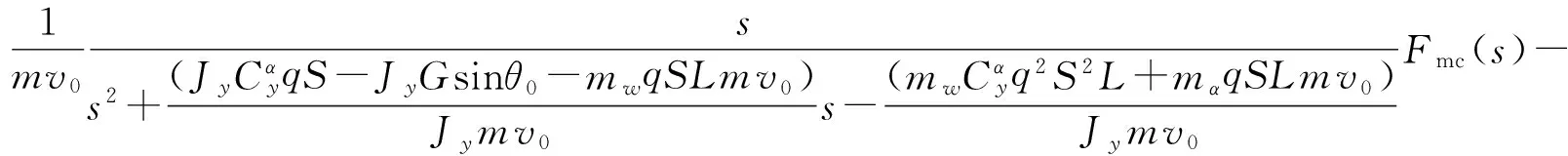
設

縱向俯仰角擾動各部分放大系數(shù)為:

得到速度俯仰角擾動運動解析解為:

(7a)

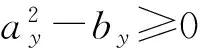
除了施工現(xiàn)場的安全檢查之外，施工技術的安全檢查很容易被忽視，導致很多建筑施工企業(yè)未能及時發(fā)現(xiàn)施工技術的缺陷，不僅不利于整個工程的建設質(zhì)量，而且還給施工項目帶來巨大的安全隱患，不利于整個項目的順利開展。

(7b)

式中：sinh()是雙曲正弦函數(shù),ay為衰減系數(shù),Ry1為縱

向擾動的振蕩頻率。

2.1.2 彈體俯仰角的解析解

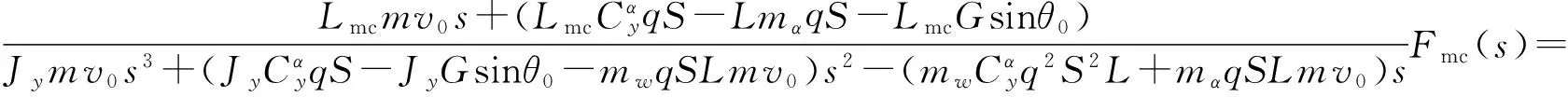
擾動運動各部分放大系數(shù)為:

得到彈體俯仰角的擾動運動解析解為:

(8a)

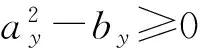
(8b)

2.2 側向脈沖擾動解析

對式(5)進行拉氏變換得到:

Jycos?s2Δψ(s)-mwcos?qSLsΔψ-mαqSLΔψ(s)+

mαqSLΔψv(s)=Fmc(s)Lmc

(9)

2.2.1 速度航向角的解析解

Δψv(s)=

設:

因為cosθ=cos?=1

可以發(fā)現(xiàn),當俯仰角較小時,側向擾動的各部分放大系數(shù)與縱向擾動一致,得到速度航向角擾動運動解析解為:

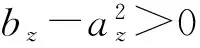
(10a)

(10b)

2.2.2 彈體航向角的解析解

Δψ(s)=

得到彈體航向角擾動運動解析解為:

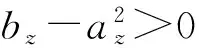
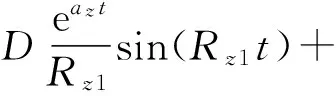
(11a)

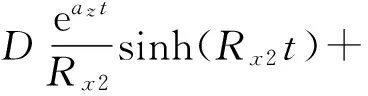
(11b)

3 Simulink建模

根據(jù)上文推導可以得到縱向和側向擾動運動的Simulink模型如圖1和圖2所示,其中建模參數(shù)為:

mα=-2.143 0 rad-1

mw=-0.018 8 rad-1

v0=554 m/s

m=3.56 kg

θ0=0.112 4°

4 仿真結果

將文中擾動建模計算結果與火箭彈6自由度彈道仿真結果進行了對比,兩者擾動運動結果如圖3～圖10所示,通過比較可以發(fā)現(xiàn),兩者結果基本一致。

圖1 火箭彈縱向擾動運動模型

圖2 火箭彈側向擾動運動模型

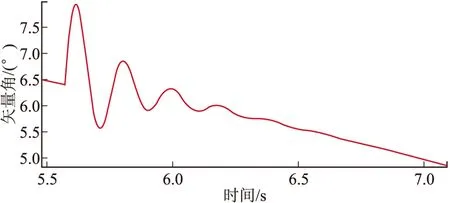
圖3 縱向彈體矢量角的擾動運動

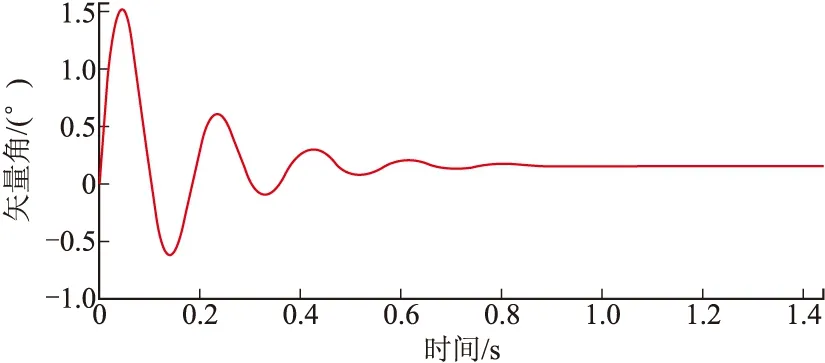
圖4 縱向彈體矢量角的仿真結果

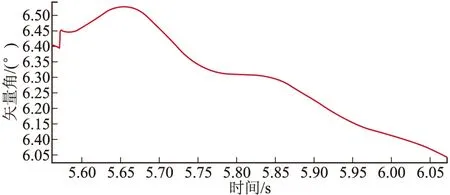
圖5 縱向速度矢量角的擾動運動

圖6 縱向速度矢量角的仿真結果

圖7 側向彈體矢量角的擾動運動

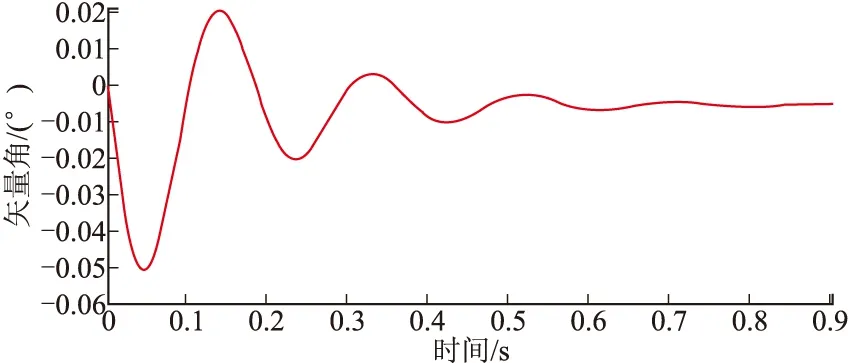
圖8 側向彈體矢量角的仿真結果

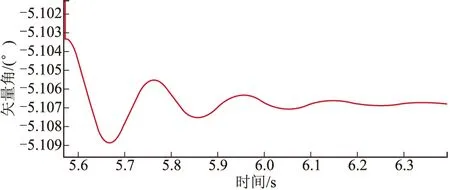
圖9 側向速度矢量角的擾動運動

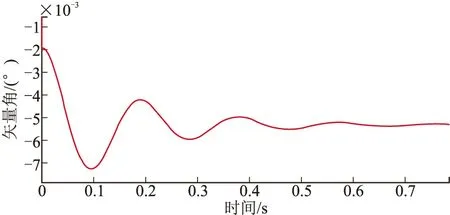
圖10 側向速度矢量角的仿真結果

5 結論

文中提出了一種利用Simulink構建火箭彈脈沖修正擾動運動模型的方法,利用火箭彈彈體與彈道夾角較小,以及脈沖發(fā)動機沖量方向和彈軸方向垂直等特征對火箭彈擾動運動方程進行了簡化,并計算了彈體和速度矢量縱向和側向擾動運動解析解。仿真結果表明,文中提出的方法能夠模擬火箭彈在空中進行脈沖修正時的擾動運動,可以應用于實驗室環(huán)境下的各種半實物仿真和擾動彈道計算中。

[1] 姚文進, 王曉鳴, 高旭東, 等. 彈道修正彈脈沖修正機構簡易控制方法 [J]. 彈道學報, 2007, 19(3): 19-22.

[2] 曹小兵, 王中原, 史金光, 等. 火箭脈沖矢量控制彈道特性分析 [J]. 彈箭與制導學報, 2005, 25(3): 67-69.

[3] 趙捍東. 脈沖發(fā)動機提供控制力的火箭彈道修正理論及技術研究 [D]. 南京: 南京理工大學, 2008.

[4] 錢杏芳, 林瑞雄, 趙亞羅. 導彈飛行力學 [M]. 北京: 北京理工大學出版社, 2000.

[5] Jan J Tuma，Ronald A Walsh. 工程數(shù)學手冊 [M]. 歐陽芳銳，張玉平，譯. 4版. 北京: 科學出版社, 2002.

A Rocket Bomb Pulse Jets Correction Perturbed Motion Simulation

YOU Peihan1,MIAO Xin2,QIAO Zhijun1,ZHU Fengchun1

(1 No.95856 Unit, Nanjing 210000, China; 2 PLA University of Science and Technology, Nanjing 210007, China)

For constructing rocket bomb’s perturbed motion semi-physical simulation, we should construct and simplify bomb’s flight motion model. In this paper, main factors that influence rocket bomb’s perturbed motion were analysed, pulse jets correction perturbed motion equations were constructed. Since the attack angle between velocity and bomb’s body is small and negligible, and pulse jets correction is perpendicular to the trajectory, we can simplify the perturbed motion equations, and get the model of rocket bomb’s perturbed motion, get attenuation coefficient and oscillation frequency’s calculation method. Simulation results show that the new simplified model can simulate rocket bomb’s perturbed motion and get similar result with 6-DOF trajectory simulation.

pulse jet correction; perturbed motion; trajectory simulation

2014-06-25

游培寒(1978-),男,江蘇南京人,工程師,博士,研究方向:航空彈藥與制導控制。

V216.7

A